不确定参数Liu系统的自适应同步在保密通信中的应用

党红刚，何万生，刘晓君

(天水师范学院 数学与统计学院，甘肃 天水 741001)

自从1990年 L.M.Pecora 和 T.L.Carroll［1］提出驱动——响应同步方法，线性和非线性反馈控制［2－3］、自适应控制［4］、模糊控制等多种不同方法都被成功地应用于混沌系统的控制与同步中。自适应控制方法由于其控制简单，物理图像明了，易于操作，使其在混沌同步的研究中占有非常重要的地位。刘崇新等于2004年提出了一个新混沌系统［5］，并研究了它的Lyapunov指数，Lyapunov维数及其吸引子的形成机制。文献［6－10］研究了不确定Liu混沌系统的控制与同步。本文以Liu混沌系统为例，采用自适应控制方法实现混沌同步，把这种同步方案应用到保密通讯中，并用Matlab数值仿真证明这种方案的有效性。

1 Liu混沌系统的模型及其混沌特性

Liu系统如下:

其中，(x，y，z)T∈R3为系统的状态变量，a，b，c，k，h 为控制参数;当选取参数 a=10，b=40，c=2.5，k=1，h=4 时，具有三个平衡点:s1=(0，0，0)，s2=(5，5，40)和 S3=(－5，－5，40)，系统的 Lyapunov指数为(1.64328，0，－14.142)。此时系统处于混沌状态。

2 参数未知的自适应同步

混沌系统的最大特点就在于系统的演化对初始条件十分敏感。在未加控制的情况下对于两个完全相同的Liu系统，若选取的初值不同，则两个系统的轨道会迅速分开变得毫不相干，如果设计适当的控制器，就可以使两个Liu系统从任何初始条件下出发都可以渐近的达到同步，设系统(1)为驱动系统，响应系统为:

其中(x1，y1，z1)T∈R3是响应系统状态向量，a，b，c，k，h 是已知参数，(k1，h1)T是参数(k，h)T的估计，u=(u1，u2，u3)T是控制器。记状态误差变量为e1=x1－x，e2=y1－y，e3=z1－z，ek=k1－k，eh=h1－h。

设计的控制器为:

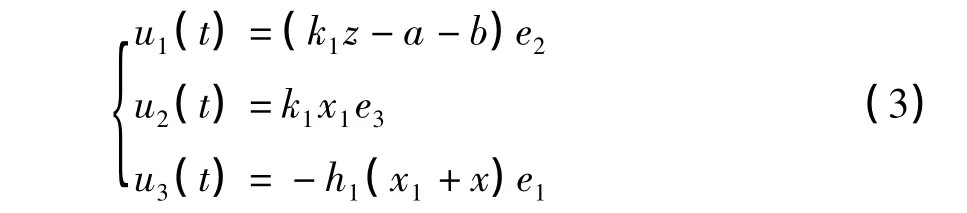
未知参数k，h自适应辨识结构为:

定理1 若选取控制器为(3)式，并且参数自适应辨识结构为(4)时，驱动系统(1)和响应系统(2)从任意初始值出发均可达到同步。

证明 (2)式－(1)式整理得误差方程:

令Lyapunov函数为

3 混沌保密通信中的应用

混沌同步应用在保密通信中的基本思路是通信系统的发送端利用混沌信号作为载波，将有用信号隐藏在混沌信号之中，而在接收端利用混沌同步恢复出传输的信号，从而实现传输信号从发送端加密到接收端解密的全过程。实现混沌保密通信的关键是发送系统与接收系统之间混沌同步。

下面以Liu混沌系统为例，基于混沌掩盖方法，用混沌信号与有用信号相加的方式，验证在(3)控制器和(4)参数识别对于响应系统(1)和驱动系统(2)在通信系统中的有效性。

设i(t)为有用信号，混合发送信号为s(t)=i(t)+x(t)，混合接收信号为˙s(t)=+x1(t)。建立如下发送系统和接收系统:

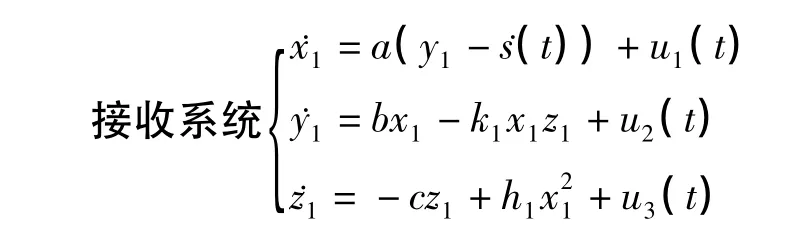
采用(3)式控制器和(4)式参数识别对上述系统进行验证。

4 数值仿真

针对驱动系统(1)和响应系统(2)构造的非线性自适应同步方案，令系统参数值为(a，b，c，k，h)=(10，40，2.5，1，4)，驱动系统向量初值为(x，y，z)=(2，2，2)，响应系统向量初值为(x1，y1，z1)=(4，4，6)，未知参数初值为(k1，h1)=(3，1)，i(t)=sin(t)，采用步长为0.01的四阶龙格－库塔函数进行仿真，图1为 e1，e2，e3的误差曲线图，图2为 k1，h1的辨识曲线图，控制器成功的实现了系统状态同步和系统不确定参数的识别。对于有用信号i(t)=sin(t)，由图3－图6可以看出，经过一段短暂的时间后，接收系统有效地恢复了传送的有用信号。

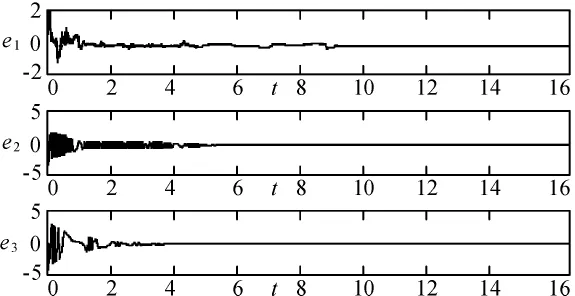
图1 非线性参数未知的同步误差曲线图

图2 参数未知的参数辨识曲线图

图3 输入的有用信号

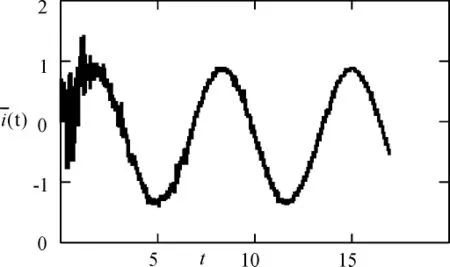
图4 输出的有用信号

图5 混合信号

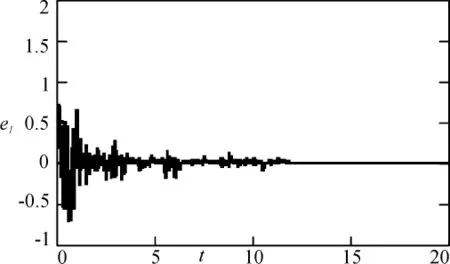
图6 输入和输出的信号误差

5 结论

本文针对保密通信的应用，以Liu混沌系统设计了一套自适应混沌同步方法，将传输信号调制到驱动系统中形成混沌信号，通过信道传输到响应系统，在响应系统中通过设计合适的控制器，并在驱动系统的k1，h1参数未知的情况下，可以使两个系统在初始值不同的情况下达到混沌同步，从而将传输信号成功解密，实现保密通信。通过实例及数值仿真表明，该方法运用广泛、方案设计简单，收敛速度快，同步时间短。

［1］L M Peoora，T L Carrol.Synchronization in chaotic systems［J］.Physical Review Letters，1990，64:821－824.

［2］J G Baraias Ramrez，L S Chen，G，Shieh.Hybrid chaotic synchronization［J］.Int J.of Bifurcation and Chaos.2003，13.

［3］Z H Guan，Y W Wang，G Chen.Impulsive control for the synchronization to Chen＇s chaotic systerms，Dynamics of continiuous［J］.Dscrete and Impulsive systerms，2003.

［4］C X Liu，T Liu，L Liu.A New Chaotic Attractor［J］.Chaos，Solitons ＆ Fract，2004，5:1031－1038.

［5］M Chen，D Zhou，Y Shang.Identicalsynchronizationof-chaoticsystems.Int.J.Bifurc.Chaos2006，16，721－729

［6］陈志盛，孙志辉，张张泰山.Liu混沌系统的非线性反馈同步控制［J］.物理学报，2005，54(6):2580－2583.

［7］陈保颖.线性反馈实现Liu系统的混沌同步［J］.动力学与控制学报，2006，4(1):1－4.

［8］彭战松，俞建宁，张建刚，等.一个新混沌系统的同步及其在密通信中的应用［J］.兰州交通大学学报，2008，27(6):160－163.

［9］赖宏慧，黄颖.基于参数辨识的自适应时滞混沌系统同步［J］.计算机仿真，2010，27(09):165－168.

［10］张永红，周焕芹，高辉.基于广义混沌序列的多幅图象隐藏算法［J］.渭南师范学院学报，2009.24(2):3－6.