双重低渗介质含启动压力梯度不定常渗流研究＊

罗二辉 王晓冬

（1.中国石油勘探开发研究院； 2.中国地质大学（北京））

低渗透储层存在低速非达西渗流现象，可用带启动压力梯度的非Darcy方程来描述其渗流过程［1－5］。存在启动压力梯度时，压力传播并非瞬时达到无穷远，而是存在一个动边界（压力扰动外边界）［6－7］。由于启动压力梯度和动边界的共同作用大大增强了不定常渗流方程的非线性和非齐次性，不少学者采取近似求解或利用数值方法进行求解［6－9］。我国许多低渗透油田储层裂缝都比较发育，其开发特征与单纯低渗透油藏不同［10］。针对双重孔隙低渗介质，许多研究者都以 Warren－Root双重介质模型为基础进行了有益探索［11－17］；然而，研究者往往忽略了动边界的存在，这虽然极大地简化了复杂非线性模型的求解难度，但不能准确反映双重低渗介质中压力传播规律［11－16］。刘启国等［17］采取格林函数法与固定边界模型相结合的数值逼近方法研究了动边界对低渗双重介质试井曲线的影响，目前还没有人给出同时考虑启动压力梯度和动边界影响的双重介质不定常渗流问题比较完整的解析结果。笔者改进了无量纲压力定义，由此消除控制方程组的非齐次性，从而解析求出动边界运动方程和压力分布。

1 考虑启动压力梯度和动边界交互作用的数学模型

假设在平面无限大双重介质低渗地层中，储层厚度均匀，介质微可压缩且各向同性，渗透率和流体粘度、体积系数等不随压力变化，忽略重力和毛管力的影响。考虑有一口生产井以定产量生产，渗流满足低速非达西定律，采用Warren－Root模型描述双重介质。首先在SI单位制下定义无量纲量。

无量纲压力、无量纲井壁压力及无量纲压力导数为

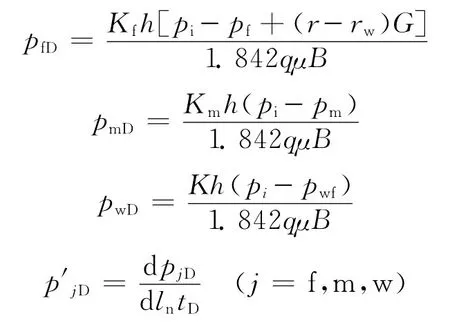
无量纲时间、无量纲径向距离和动边界为

无量纲启动压力梯度为

在上述无量纲定义下，双重介质不定常渗流模型为

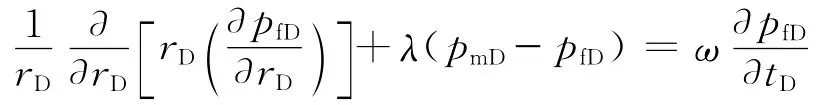
其中：

初始条件为

内边界定产条件为

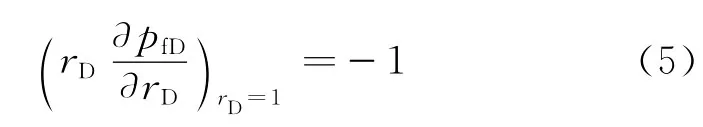
外边界移动界面条件为

对方程（1）～（7）作Laplace变换，则方程和定解条件变成如下形式：

其中：

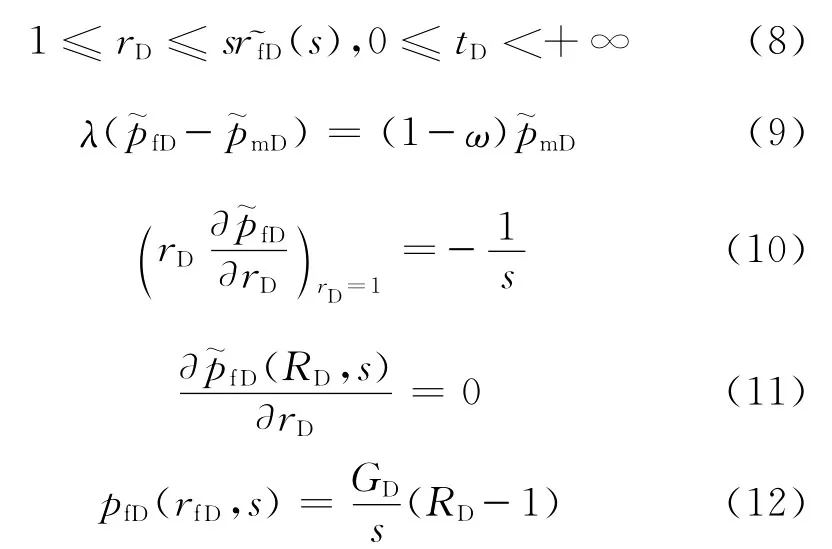
联立方程（8）和方程（9），得

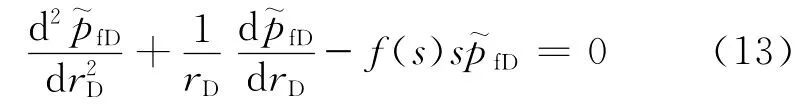
式（8）～（13）中：

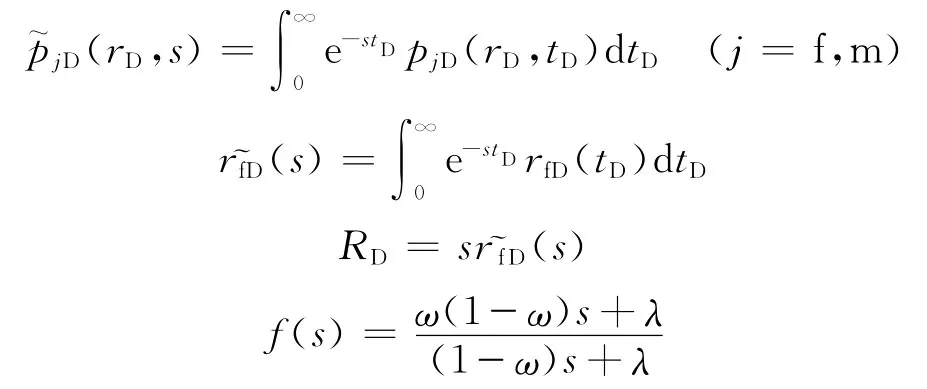
2 定解问题的解

解析求解方程组（10）～（13）可分为两步，先由方程（10）、（11）、（13）组成（边界移动的）封闭储层不定常渗流控制方程组进行解析求解，再将解析解式代入式（12）得到动边界运动方程，即：

（1）对由式（10）、（11）、（13）组成的方程组解析求解，得到Laplace空间压力分布解式为

（2）将式（14）代入式（12）得到动边界运动方程为

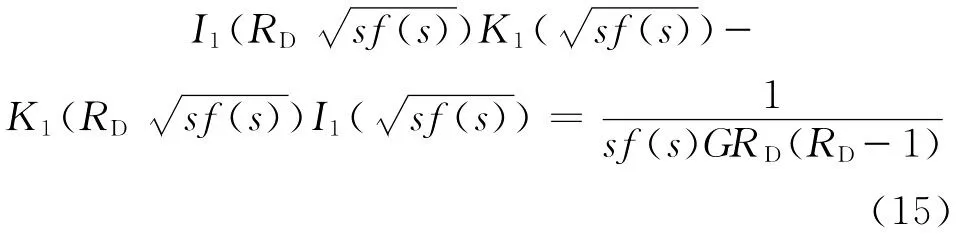
在得到式（15）的过程中应用了Bessel函数相应的Wronskians关系式。

计算过程中首先利用牛顿迭代方法在Laplace变换域中计算式（15），再采用Stehfest数值反演方法［18］计算式（14），得到储层无量纲压力分布或井壁压力分布。

有效井径模型和Duhamel褶积分别包含了表皮效应和井筒存储效应，据此定义无量纲井筒存储系数

式（16）中：C 为井筒存储系数，m3/MPa。

根据Duhamel褶积，在Laplace变换域中受井筒存储和表皮效应影响的井底压力计算方法［19］是

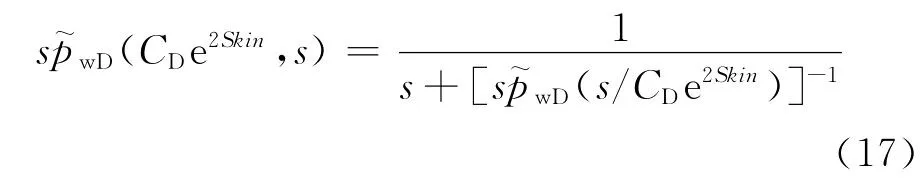
式（17）中：Skin为表皮因子（无量纲）。

3 敏感参数分析

根据式（14）、（15）绘制出动边界传播规律和井壁压力动态特征曲线如图1～4所示。由图1～4可知，双重低渗介质中压力动态变化经历3个阶段：裂缝系统的渗流、基岩系统向裂缝系统的窜流、基岩系统和裂缝系统混合流。由于启动压力梯度和动边界的影响，压力导数曲线在后期不再表现为水平直线段，而是呈现上翘趋势，这表明由于动边界的作用，即使考虑为无穷大边界，单井的控制范围也是有限的。

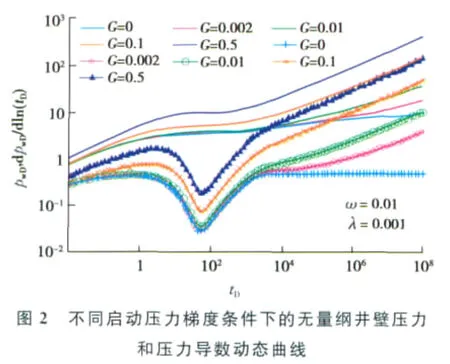
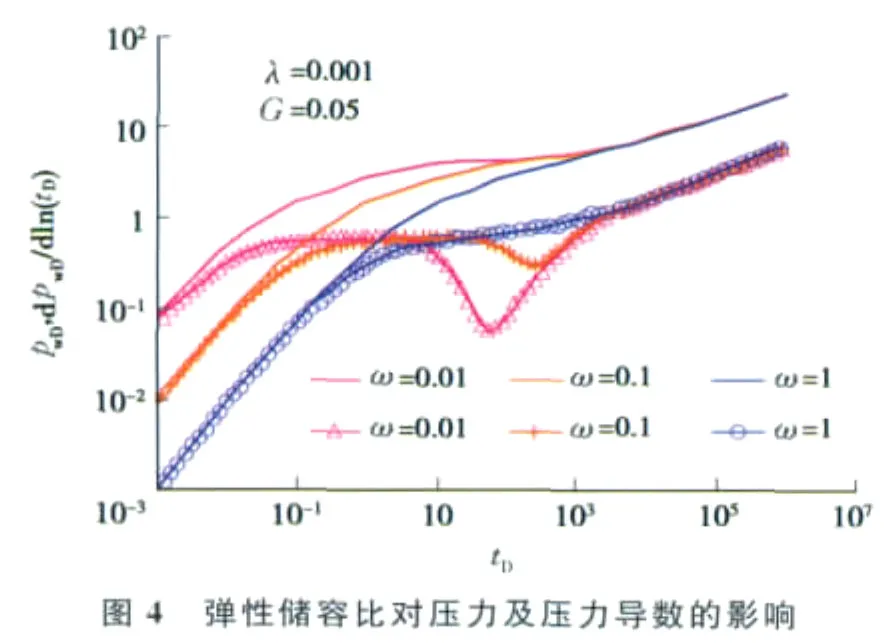
图1示出了启动压力梯度对动边界传播规律的影响，在其它参数不变的情况下，启动压力梯度增大，压力扰动传播的速度变慢，曲线中间的平稳段是由于基岩系统向裂缝系统的窜流引起，代表了双重介质有别于单纯介质的过渡流特征。图2示出了启动压力梯度对井底压力及压力导数的影响，在其它参数一定时，由于启动压力梯度和动边界的影响，压力导数曲线后期出现上翘；随着启动压力梯度增加，无量纲压力增加，而无量纲压力是正比于压力降落的，它的增加说明渗流过程中能量损失增加。图3、4分别为窜流系数和弹性储容比对压力及压力导数曲线的影响，可以看出，两者区别于中高渗双重介质的特征在于由动边界作用引起的压力导数曲线的后期上翘特征。

根据式（17）计算得到受参数团CDe2Skin和GD影响的不稳定试井分析典型曲线图版（图5）。图5表明，由于受到井筒存储的影响，不稳定压力变化早期不能体现出启动压力梯度的特别影响，但进入中后期井筒存储影响渐弱，启动压力梯度和动边界的作用变得明显，这与图2的结果一致。

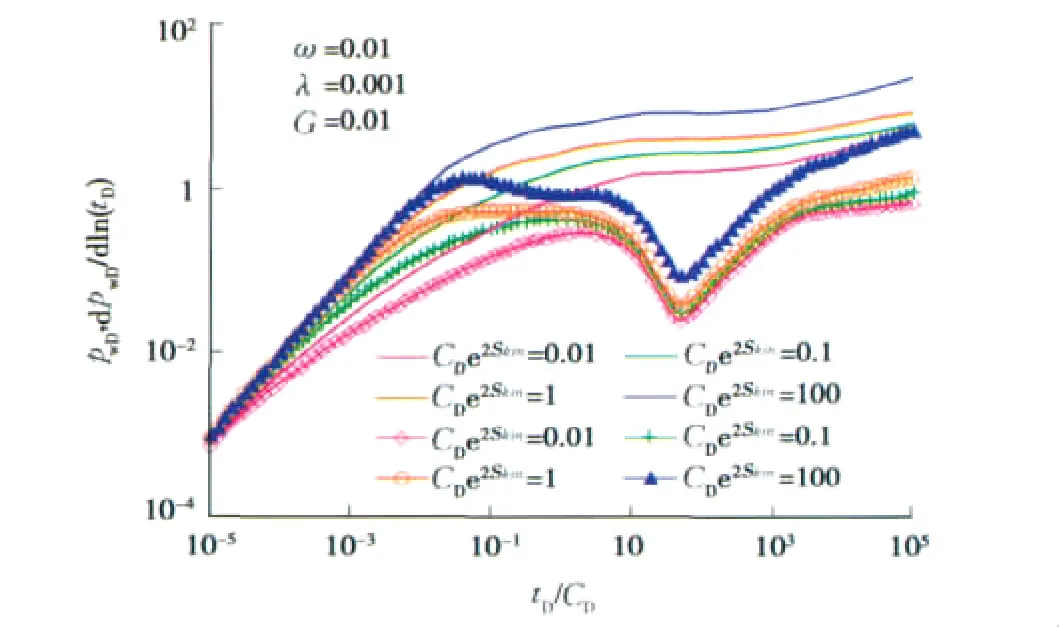
图5 不同CDe2Skin对压力及压力导数的影响

4 结论

（1）通过引入新定义的无量纲压力，对非齐次非线性非稳态渗流方程进行无量纲化，在保证初始条件方程齐次性的同时消除了控制方程的启动压力梯度非线性项，从而方便进行解析求解。

（2）低渗双重介质敏感参数分析结果表明，启动压力梯度对动边界传播、井壁压力及压力导数曲线有较大影响，并且动边界引起压力导数曲线后期上翘；不同弹性储容比和窜流系数条件下低渗双重介质井壁压力导数曲线区别于中高渗双重介质之处在于其后期有上翘特征，这表明低渗双重介质渗流过程中能量损失增加。

（3）给出的低渗双重介质考虑启动压力梯度、包含井筒存储和表皮效应的不稳定试井分析典型曲线图版表明，由于受到井筒存储的影响，不稳定压力变化早期不能体现出启动压力梯度的特别影响，但进入后期，启动压力梯度和动边界的作用变得明显。

符号注释

Kf—裂缝渗透率，mD；Km—基岩渗透率，mD；h—储层厚度，m；q—井产量，m3/d；μ—原油粘度，mPa·s；B—原油体积系数；pi—原始地层压力，MPa；pf—裂缝系统压力，MPa；pm—基岩压力，MPa；t—延续时间，h；φ—储层孔隙度，f；c—系统压缩系数，1/MPa；rw—井筒半径，m；rf—压力扰动外边界，m；G—启动压力梯度，MPa/m；ω—弹性储容比；λ—窜流系数；Ij（x）—j阶第一类变型Bessel函数（j＝0，1）；Kj（x）—j阶第二类变型Bessel函数（j＝0，1）；s—Laplace变换量。

［1］ 蒋利平，李茂，姜平，等.综合考虑启动压力和压敏效应的低渗透油藏渗流规律研究［J］.中国海上油气，2009，21（16）：388－392.

［2］ 陈钟详.渗流力学的近况动向和展望［J］.力学学报，1974，18（1）：19－21.

［3］ 冯文光.非达西低速渗流的研究现状与展望［J］.石油勘探与开发，1986，13（4）：76－80.

［4］ 闫庆来，何秋轩，尉立岗，等.低渗透油层中单相液体渗流特征的实验研究［J］.西安石油学院学报，1990，5（2）：1－6.

［5］ 黄延章.低渗透油层非线性渗流特征［J］.特种油气藏，1997，4（1）：9－14.

［6］ PASCAL H.Nonsteady flow through porous media in the presence of a threshold gradient［J］.Acta Mechanica，1981，39（3－4）：207－224.

［7］ 刘慈群.有起始比降固结问题的近似解［J］.岩土工程学报，1982，4（3）：30－34.

［8］ 李凡华，刘慈群.含启动压力梯度的不定常渗流的压力动态分析［J］.油气井测试，1997，6（1）：1－4.

［9］ 程时清，张盛宗，黄延章，等.低速非达西渗流动边界问题的积分解［J］.力学与实践，2002，24（3）：15－17.

［10］ 李道品，等.低渗透砂岩油田开发［M］.石油工业出版社，1997：162－166.

［11］ 冯文光，葛家理.单一介质、双重介质中非定常非达西低速渗流问题［J］.石油勘探与开发，1985，12（1）：56－62.

［12］ 冯文光，葛家理.单一介质、双重介质非达西低速渗流的压力曲线动态特征［J］.石油勘探与开发，1986，13（5）：52－57.

［13］ 程时清，李功权，卢涛，等.双重介质油气藏低速非达西渗流试井有效井径数学模型及典型曲线［J］.天然气工业，1997，17（2）：35－37.

［14］ 贾永禄，李允，吴小庆，等.特殊开采方式低速非达西渗流试井模型研究［J］.西南石油学院学报，2000，22（4）：37－40.

［15］ 霍进，贾永禄，蒋维军，等.双重孔隙介质低速非达西渗流油藏DST段塞流压力动态分析［J］.江汉石油学院学报，2004，26（3）：119－121.

［16］ 张允，王子胜，姚军，等.带启动压力梯度的双孔压敏介质压力动态及其应用研究［J］.水动力学研究与进展，2007，22（3）：332－337.

［17］ 刘启国，杨旭明，魏红梅，等.动边界影响的低渗双重介质油气藏试井解释模型［J］.西南石油学院学报，2004，26（5）：30－33.

［18］ STEHFEST H.Numerical lnveysion of Laplace transforms［J］.Communications of the ACM，1970，13（1）：47－49.

［19］ 刘慈群.垂直裂缝井的各类试井分析方法综述［J］.石油勘探与开发，1995，22（1）：59－60.