基于灰色逻辑斯蒂模型的林木生长量研究

覃 力，唐学冰，马友湖

(1.建始县三里林站，湖北 建始 445300; 2.建始县国营高岩子林场，湖北 建始 445300)

逻辑斯蒂(Logistic) 曲线方程是荷兰生物数学家P.F.Verhulst为研究人口增长过程于1938年而导出的，但长期被湮没，直到20 世纪20 年代才为R.Pearl和L.T.Reed重新发现并应用.Logistic曲线方程既应用于社会经济现象研究，也广泛应用于林木生量的预测等研究.林木的生长是一个非常复杂的过，其特点是开始增长缓慢，而在以后的某一范围内迅速增长，达到某限度后增长又缓慢下来.曲线略呈拉长的“S”型[2-3].本文将待测对像的平均树高看成是在一定范围内变动的灰色量,利用灰色的建模技术,探讨Logistic方程参数的估计，称之为灰色逻辑斯蒂模型，并结合实例说明计算过程与建模效果.

1 Logistic模型

当种群在一个有限空间增长时，随着种群密度的上升，对有限空间资源的竞争必将加剧，从而影响种群的生殖率和存活率，以至降低种群的实际增长率，最后种群停止增长，有时甚至下降.因此，可设想在一个环境条件下，有一个允许的最大种群值K，通常称K为环境容纳量，Logistic方程[3]可描述这种有限空间中的种群生长:dH/dt=γH((K-H)/K).

其中:K为环境容纳量；H为t时刻的种群数量；γ为种群内禀增长率.方程的积分式为:

H=K/(1+αe-γt)

(1)

其中:α为积分常数.

2 模型参数的求解

2.1 线性回归求解

式(1)虽为非线性方程，但K为环境的最大容纳量，可具专业知识确定其值，由此变为了常量.因此可转化为一元线性回归方程，采用最小二乘法求解.式(1)可转化为：K/H-1=αe-γt两边取对数可得:

ln[K/(H-1)]=lnα-γt

(2)

今y=ln[K/(H-1)],a=lnα,则变成普通的一元线性回方程，可据最小二乘法求解.

2.2 GM(1，1)求解

对某个事物发展变化的大小与时间所作的预测，称之为数据列.GM(1，1)模型为单序列的一阶动态模型，是常用的一种灰色数列预测模型[5-8].

设原始无明显规律的时间序列{X(0)(i)}(i=1,2,…,n)作一次累加生成，得到序列：

X(1)={X(1)(1),X(1)(2),…,X(1)(n)}，

dX(1)/dt+aX(1)=u

(3)

(4)

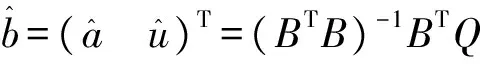
(5)

根据灰色系统理论，有指数变化规律的原始数列可以不做生成处理,而直接进行灰色建模[9].对等时间间隔的数据，式中B为式(6)，Q为式(7)：

(6)

Q=(X(0)(2)-X(0)(1),X(0)(3)-X(0)(2),…,X(0)(n)-X(0)(n-1))T

(7)

显然式(1)可变为:

高敦施工是公路桥梁建设中的重要环节，我国高敦施工工艺技术得到极大提高，高墩施工关系着桥梁建设的安全性，在高墩施工中要严格按相关技术标准执行，避免出现工程质量安全问题，促进我国公路桥梁建设的稳健发展。

1/H=(1+αe-γt)/K

(8)

令x=1/H,B=1/K则式(8)可变为:

x=B(1+αe-γt)

(9)

对式(9)求导可得:

dx/dt=-γαBe-γt

(10)

式(10):dx/dt=-γαBe-γt=-γB(1+αe-γt)+γB,即:

dx/dt+γx=γB

令γ=a,γB=u可得式(11):

dx/dt+ax=u

(11)

式(11)中的参数a,u可通式(5)求得,则式(1)中的γ=a,K=γ/u，α=(K/H0-1)eγt0.

3 实例分析

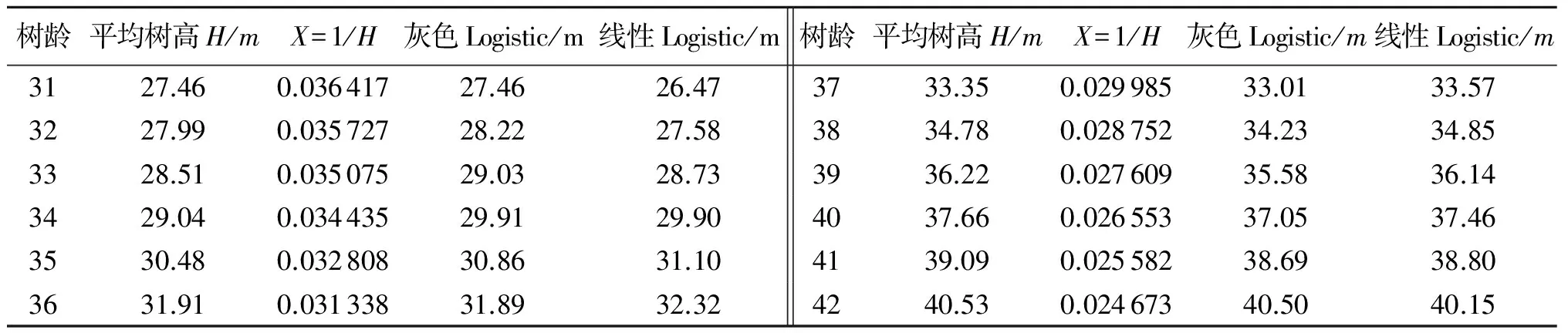
为了研究林木的生长规律，选取了对日本落叶松调查的一组数据，详见表1.基于表1,对林木平均树高的生长进行预测，可将式(1)变为：

H=K/(1+αe-γt) (12)

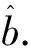
(13)

由式(13)中的a=-0.017 0,u=-0.001 6,则式(12)中的γ=-0.017,K=10.702 2,当H0=27.46,t0=31代入α=(K/H0-1)eγ(t0-199 1)得α=-0.599 98.于是平均树高的灰色逻辑斯蒂方程为；

H灰=10.702 2/(1-0.599 98e0.01 7(t-30))

(14)

用线性回归法求得的平均树高的Logistic模型参数时，取K=100[5]，可得式(15)：

H线=100/(1+2.940 265 843e-0.056 6(t-30))

(15)

由式(14)、(15)估计的平均树高详见表1.

[1] 崔党群.生物统计学[M].北京:中国科学技术出版社,1994.

[2] 孟宪宇.测树学[M].北京:中国林业出版社,1996.

[3] 蔡贤如.Logistic方程参数优化估计方法研究[J]．沈阳农业大学学报，1995，26(1)：64-67.

[4] 邓聚龙.灰色系统基本方法[M].郑州：河南大学出版社,1987.

[5] 刘思峰,郭天榜,党耀国.灰色系统理论及其应用[M].北京：科学出版社，1999:102-155.

[6] 易德生,郭萍.灰色系统理论与方法：提要，题解，程序，应用[M]．北京：石油工业出版社，1992:128-162.

[7] 秦文安，马友平.利川市红椿沟日最大降雨量的GM(1，1)的预测与修正[J].湖北民族学院学报：自然科学版,2010，28(4)：474-477.

[8] 马友平，张志华，艾训儒.城市化水平的灰色遗传算法预测[J].湖北民族学院学报：自然科学版,2008，26(1)：68-71.