一类修正的积分型Shepard算子在Olicz空间中的逼近

田 园

(湖北民族学院 理学院，湖北 恩施 445000)

对于f(x)∈C[0,1]，著名的Shepard算子指:

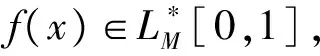
1 若干引理

引理1[1]存在两个常数C1和C2，使得C1ω(f,t)M≤K(f,t)M≤C2ω(f,t)M.

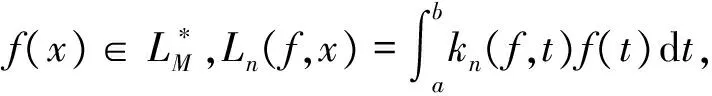
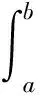
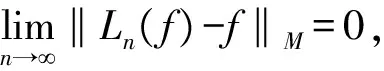
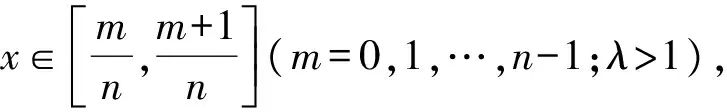
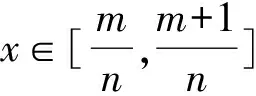
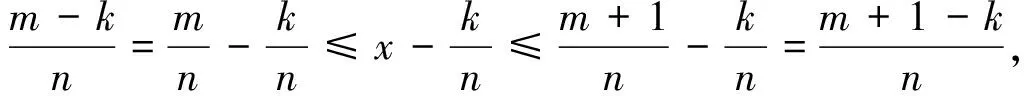
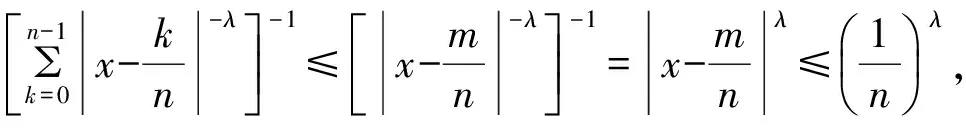
2 定理1的证明

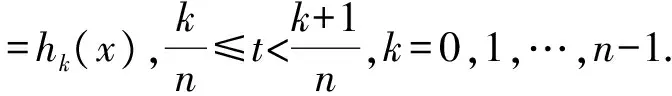
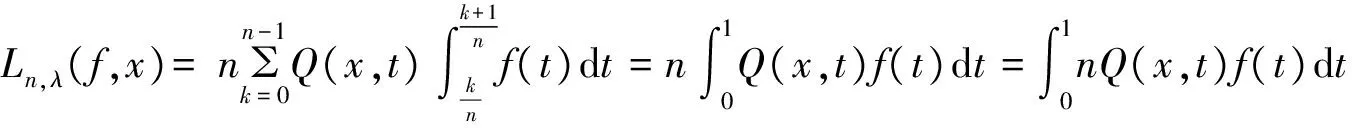
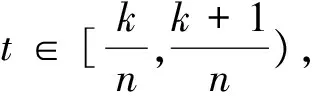
由此可知，nQ(x,t)为Ln,λ(f,x)的核函数，且满足引理2的条件(i).

由文献[4]可知，∀ε>0，当n充分大时，∀x∈[0,1]，都有|Sn,λ(f,x)-f(x)|<ε/2.

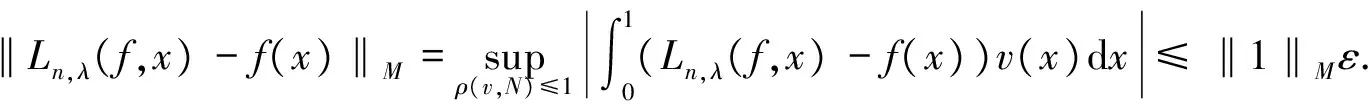
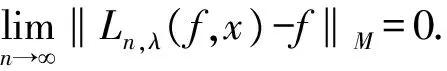
[1] 吴从炘，王延辅.奥尔里奇空间及其应用[M].哈尔滨：黑龙江科学技术出版社，1983.

[2] Wu Garidi.On approximation by polynomials in Olicz spaces[J].Approximation Theory and its Applications,1991,7(3):97-110.

[3] 吴嘎日迪.一类新型Kantorovich算子在Olicz空间内的逼近性质[J].内蒙古师范大学学报：自然科学汉文版，2006,35(3):253-257.

[4] Somorjai G. On a satuation problem[J].Acta Math Hungar,1978,32:377-381.

[5] 谢庭藩,周颂平.实函数逼近论[M].杭州：杭州大学出版社,1997.

[6] 冯悦，吴嘎日迪.Shepard算子在Olicz空间内的逼近等价定理[J].内蒙古师范大学学报：自然科学汉文版，2010,39(6)：565-568.

[7] 王建力.修正的Shepard型算子的Lp-逼近[J]. 数学杂志，2003,23(3):285-289.