破损进水舰船非线性横摇运动的实验研究
浦金云,刘 辉,吴向君,陈晓洪
(海军工程大学 船舶与动力工程学院,武汉 430033)
破损进水舰船非线性横摇运动的实验研究
浦金云,刘 辉,吴向君,陈晓洪
(海军工程大学 船舶与动力工程学院,武汉 430033)
通过设计破损舰船非线性横摇运动实验,对不同状态下的船模进行定频率变波高和定波高变频率的横摇激振试验,探讨舰船横摇运动的水动力特性随横摇频率和横摇幅角变化规律,分析Ⅱ类和Ⅲ类进水舱对破损舰船横摇运动的水动力特性的影响。运用混沌信号识别技术分析破损舰船进水后横摇运动的混沌特性,验证数值仿真的结果,预报破损舰船在规则波中的横摇运动的幅频响应和相频响应。
横摇运动;破损舰船;混沌;响应
1 引 言
在统计的船舶航行倾覆事故中,由于破损进水导致船舶倾覆的事故为数不少,而这些船舶在设计时都具有足够的稳性,主要原因是目前设计规范都是在船舶流体静力学的基础上制定的,而实际舰船破损进水后的横摇特性即使在规则波中也会表现出不规则的复杂运动形式,通过非线性分析说明了它们是无规则的,回复力矩的非线性特性和进水的影响将导致产生复杂的非线性运动[1]。
舰船可能会由于碰撞、触礁、或被武器命中产生大面积的破口进水[2],这种情况下舱内的进水将会随横摇运动产生两个方面的变化。一是进水量的增减变化;二是破损舱内液面随船波动,这类破损进水舱为Ⅲ类舱[3]。Ⅲ类舱的破损进水将使舰船的横摇运动更加复杂,目前在这方面的研究更少[4]。
为了更好地研究舰船在规则波中的横摇运动规律,研究讨论破损进水在横摇运动中对舰船的耦合作用,分析破损进水后舰船横摇运动的混沌特性。本文通过设计破损舰船非线性横摇运动实验,对不同状态下的船模进行定频率变波高和定波高变频率的横摇激振试验,验证作者前期数值仿真的结果,更好地预报破损舰船在规则波中的横摇运动的幅频响应和相频响应。
2 实验船模的设计
为了确切地研究横浪对实际舰船摇荡的影响,本试验采用的是相似于某实船的船体模型,其缩尺比λ=50。相应于实船,船模的设计水线从首至尾设有肋骨号为0~284#,肋骨间距为1cm。船模的主尺度长Lmax为3.11m,设计水线L长为2.84m,甲板宽Bmax为0.344m,设计水线宽B为0.32m,设计吃水T为0.092m,型深H为0.196m,船模在设计吃水T时的正常排水量为42.24kg[6]。
根据相似性理论,船模与实船的相同参量之间有一个固定的对应关系,各参量之间的相似条件比如表1所示。

表1 船模与实船各参量间的相似条件Tab.1 The similar scale of parameters between the ship model and the real ship
3 实验测量装置的确定

实验是在华中科技大学船池实验室进行,船模及试验水池如图1所示,该水池是国际水池会议成员单位,设施先进可靠[7]。实验设备包括水池、造波机、陀螺仪、浪高仪和信号采集系统,具体如下:
(1)耐波性水池的尺寸为长170m,宽6m,深4m。水池一端为造波机,另一端采取了被动消波措施,以减少波激振动试验时回波的干扰作用,水池的一边也采取了被动消波措施,以便试验完后快速消波。
(2)造波机是1987年从美国进口冲箱式造波机。由六个冲箱组成,可用于造规则波和不规则波,造波波长范围为2~9m,最大波高为 25cm。
(3)陀螺仪的横摇测量范围为0~±50°;信号幅值测量偏差≯±0.1% 。
(4) 浪高仪型号为 WS-540,测量范围为 0~±250mm;非线性为±0.1%F.S;偏差为±0.01%/F.S./℃;最大响应速度为≮1.75m/sec。
(5)信号采集系统为数字采集系统,其采样频率可达5kMZ,主要参数为8双/16单模拟信号输出通道,2模拟信号输出通道,输入/输出模拟信号转换分辨率为12bit。
4 波激横摇试验方案的设计
4.1 波激横摇试验的原理
陀螺仪与船模一起横摇,当横摇稳定后,采集系统可得到实时的波浪曲线和相应的横摇运动曲线。进一步测量和处理,即可得到波浪的波高H和频率f、船模的横摇幅值φr、横摇频率f及横摇运动相对于波浪的相位差δ等数据。
根据测得的波高H和频率f,则波长l=1.56/f2,波浪扰动力矩幅可由下式求得:
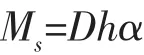
式中,D为排水量;h为初稳心高;α为波倾角,波倾角由下式求得:
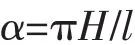
对于每一次横摇激振试验,可得到波浪扰动力矩幅Ms、波频ω、横摇幅角φr和横摇运动相位差δ等数据。
4.2 波激横摇试验
造波机所产生的规则波浪的要素包括波长、波高和周期,可以用理论公式λ=1.56TB2确定波长,由经验公式hw≈0.17λ3/4,TB=2π/n确定波高和波浪周期,其中n为造波机的振荡频率。
为了使船模试验结果能按照概率论中的线性理论预估实船的相应运动,要求模型的横摇运动与波高成线性关系。试验资料[8-9]表明,在波高hB=Lm/40~Lm/30时一般能满足运动与波高成线性关系。通常实验室的波高取Lm/50(Lm为船模长度),则在本次试验中,波高范围定为6~20cm。波浪的高度用浪高仪测量,在水池中定点测量波高时,浪高仪与造波机的距离不小于20m,而与池壁的距离不小于1.5m,以提高波高的测量精度。
波激横摇试验的目的是获得进水船模横摇运动的非线性响应,并用于预报横摇运动,试验内容包括定频率变波高试验和定波高变频率试验。
(1)定频率变波高试验
试验目的是获得船模横摇时的水动力系数与横摇幅角和横摇频率之间的关系,从而辨识出船模横摇时的非线性附加质量和横摇阻尼的各次系数。根据自由横摇试验得到的横摇固有周期Tθ,选定横摇频率ω,控制和调节一系列不同的波高hw,则可以相应地测定一系列船模稳定横摇时的横摇摇幅角φr和横摇运动相对于波浪的相位差δ。利用这些试验数据,就可获得非线性水动力特性,并可用于预报横摇运动。
(2)定波高变频率试验
试验目的是获得一定的波浪力矩作用下,船模横摇的幅频响应和相频响应特性。根据模型运动与波高成线性关系的要求,选定试验波高,控制和调节一系列不同的横摇频率ω,则可以相应地测定一系列船模稳定横摇时的横摇摇幅角φr和横摇运动相对于波浪的相位差δ。从而获得船模横摇的幅频响应和相频响应特性,并可用于检验前面的预测结果。
5 破损舰船船模试验结果及分析
5.1 完整船模试验
完整船模试验进行了自由横摇试验、定频率变波高试验和定波高变频率试验,文中选取定频率变波高试验(T=2.70s)和定波高变频率试验(H=7cm)的试验测量结果,具体见表2和表3。

表2 定频率变波高试验 (T=2.7s)Tab.2 The experiment of fixed frequency and varied wave high(T=2.7s)
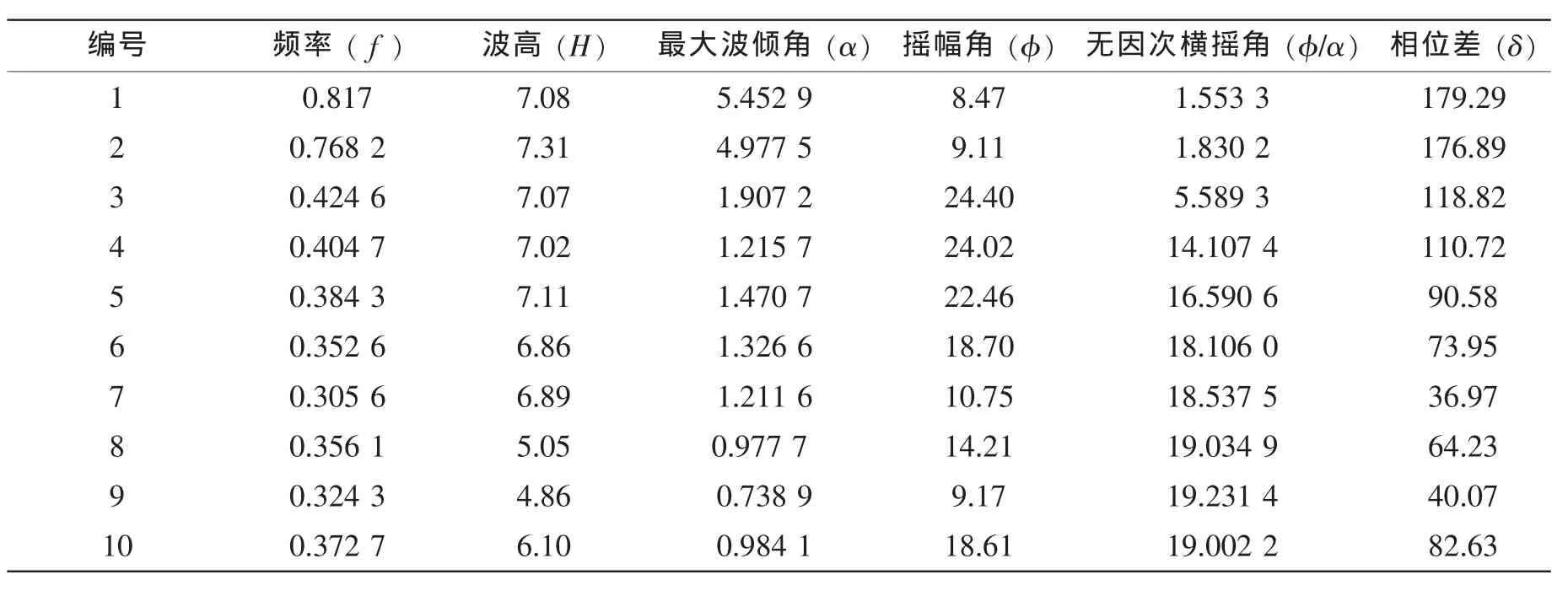
表3 定波高变频率试验 (H=7cm)Tab.3 The experiment of fixed wave high and varied frequency
5.2 破损舰船船模试验
对每种船模状态进行规则波正横激励,激励波长为2~6m,间隔0.5m,激励波陡从1/40~1/25。试验结果通过观察信号的时间历程、功率谱分析方法和时间延迟的相空间重构来识别混沌信号。
由各状态试验数据的频谱图可以看出,在单频的正弦正横浪的激励下,破损船的横摇运动中不仅包含波频成份的运动,也存在次谐运动、超谐运动以及组合频率的运动,在一定的船模参数、进水参数及波浪激励力矩参数条件下,其运动还可能是混沌的,其中具有负初稳度的船模的运动更加复杂。
5.2.1 Ⅱ类舱进水时进水量对横摇运动的影响
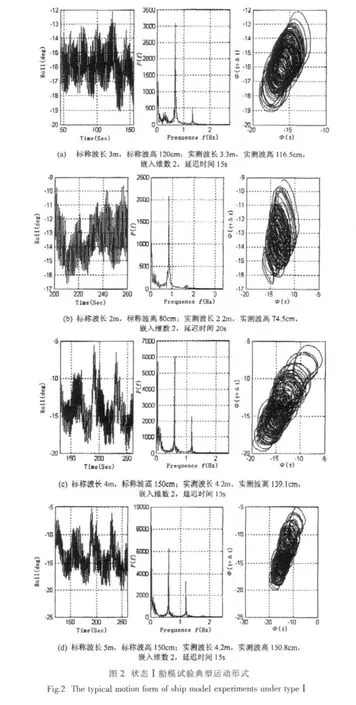
文中选取状态Ⅰ和状态Ⅱ两种状态下的试验数据进行对比分析,考察船模阻尼和进水舱自由液面大小相同情况下舱室进水量对船模运动的影响。状态Ⅰ为Ⅱ类舱对称进水,负初稳度,三舱进水,进水量8.36kg;状态Ⅱ为Ⅱ类舱对称进水,负初稳度,三舱进水,进水量4.2kg。试验数据的时间历程、功率谱和重构相空间结果如图2(a,b,c,d)和图3(a,b,c,d)所示。
对比图2和图3可以看出,进水量较大时,船模运动的次谐成份更丰富,超谐运动的能量更高,激振频率处的能量被分散到超谐运动和次谐运动中,因而激振频率处的能量更低。对图2所示运动的频谱的进一步分析表明,其运动不仅包含2倍于激振频率的超谐运动,还包含1/2、1/4、1/8倍激振频率的运动,即2倍、4倍、8倍于波浪激励力周期的运动;但Lyapunov指数计算表明,其运动仍是周期的。为了观察可能的进一步的倍周期过程,调整激励力参数进行了进一步的试验,但在所试验的波浪激励力频率和所能达到的激励力矩幅值范围内,对状态Ⅰ和状态Ⅱ,均未观察到混沌运动。这一结果与数值仿真结果是相符的,状态Ⅰ、Ⅱ的自由液面大小与数值仿真中的小自由液面状态相同,在数值仿真中虽然出现了混沌运动,但其所要求的激励力矩大小在实际船模试验中无法达到,因而在实际试验中不可能观察到混沌运动。
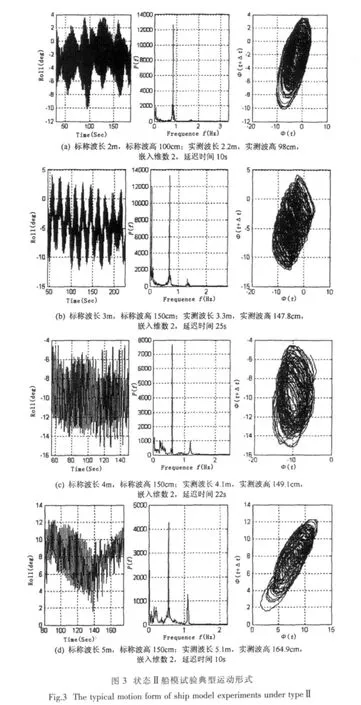
5.2.2Ⅱ类舱进水时自由液面大小对横摇运动的影响
文中选取状态Ⅰ和状态Ⅲ两种状态下的试验数据进行对比,分析具有相同进水质量时,自由液面面积大小对船模运动的影响。状态Ⅰ及其试验数据结果如5.1节所示,状态Ⅲ为Ⅱ类舱对称进水,负初稳度,五舱进水,进水量8.36kg。状态Ⅲ的试验数据的时间历程、功率谱和重构相空间结果如图4(a,b,c)所示。
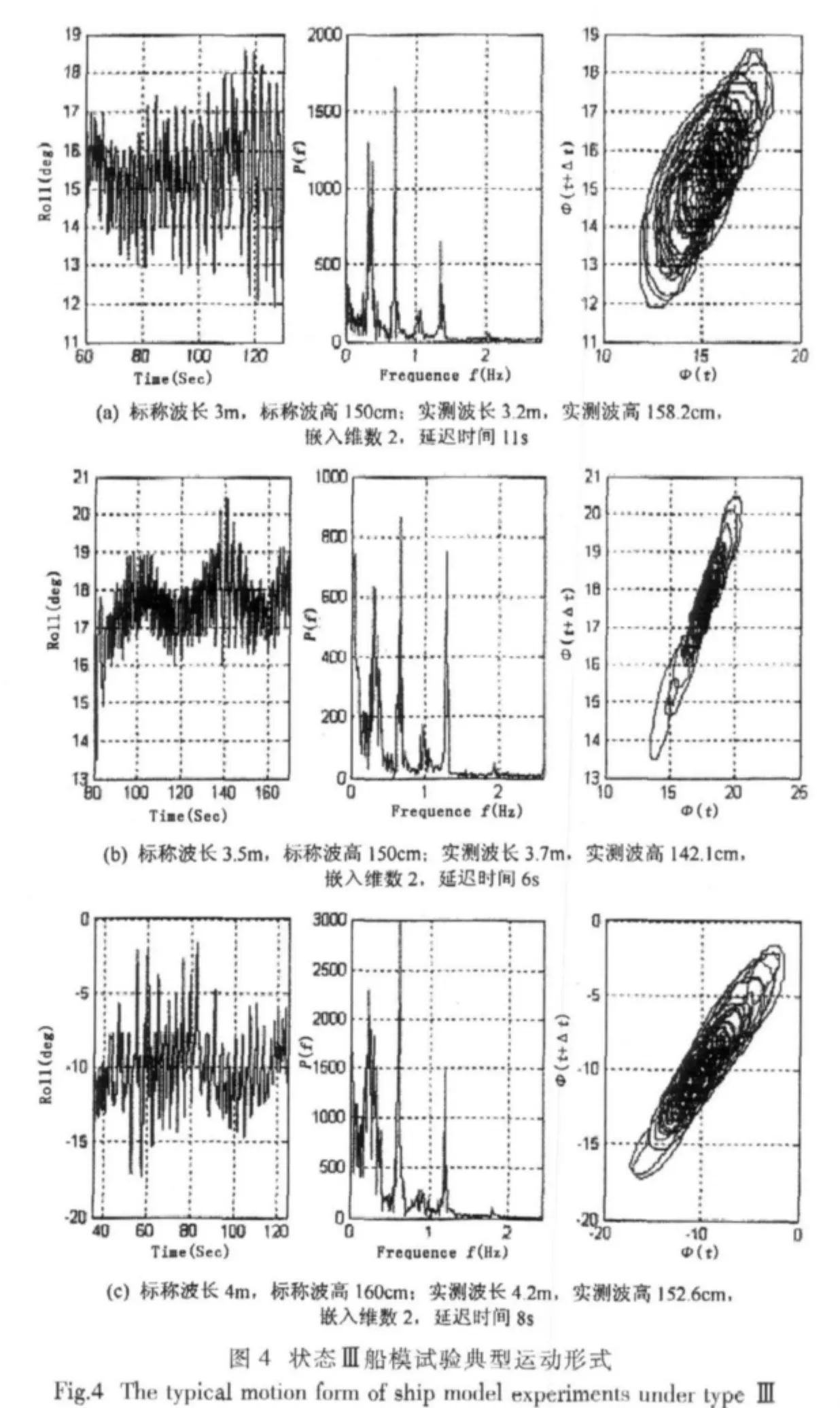
状态Ⅰ为三舱进水,状态Ⅲ为五舱进水,自由液面面积不同,由图4可以看出,在自由液面面积较大时,船模的次谐运动和超谐运动更为明显,在部分波浪激励力参数条件下,还出现了次谐成份或(和)超谐成份能量大于激振频率成份能量的情形。试验时对船模运动的目视观察中可以发现明显的2倍、4倍于波浪激励力周期的运动。
状态Ⅲ与数值仿真中的标准状态相同,由混沌参数区域图可知,在该状态下,要求波浪激励力的波倾角在1/20左右才会出现混沌运动。为验证该状态的数值仿真结果,试验中曾将波浪激励的波倾角调整到1/20及以上,但此时的波浪波形发生畸变,试验结果缺乏意义。
5.2.3 Ⅲ类舱对称进水时的横摇特性
文中选取状态Ⅳ下的破损船,分析其受横摇试验的横摇特性。状态Ⅳ为Ⅲ类舱对称进水,负初稳度,四个Ⅱ类舱对称进水5kg,一个Ⅲ类舱对称进水3kg(仅指船正浮状态时的进水量),试验数据的时间历程、功率谱和重构相空间结果如图5(a,b,c)所示。
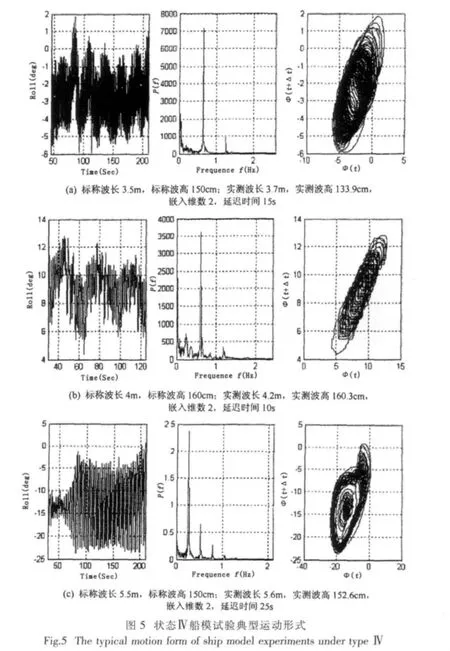
具有Ⅲ类进水舱的破损船出现混沌运动时的波浪激励力矩幅值很大,超出了实际能达到的波浪激励力范围,在实际的横摇试验中确实未观察到混沌运动现象,验证了数值仿真结果。
文献[10]指出,在波浪激励力参数不变的情况下,破损船横摇的振幅可能因为外部的干扰而发生变化,这一现象在Ⅲ类进水舱船模试验中得到重现,如图5(c)所示。文献[10]中采用外部干扰的方式使船模运动由小振幅横摇转入大振幅横摇,而在图5(c)所示的试验中,船模受到的干扰为由随机因素引起的波浪激励力的微小变化,由于干扰力的作用,船模由小振幅横摇转入并稳定在大振幅横摇状态。
6 结 论
对具有Ⅱ类进水舱和Ⅲ类进水舱对称或不对称进水的破损船受正横规则波激励的试验研究表明,破损船在规则波激励下的横摇运动十分复杂,其运动形式与船模参数(阻尼、稳性)、进水参数(进水量、自由液面大小、进水类型)和波浪激励力矩参数(波长、波高)有很大的关系。随系统参数和外部激励的不同,其运动可能为单频的,也可能为多频的;可能是周期的,也可能是混沌的。在实际的波浪激励力矩参数范围内,具有正初稳度的破损船的横摇响应一般为周期响应,而具有负初稳度的破损船则可能出现非周期响应。对于负初稳度、Ⅱ类进水舱的破损船,具有较大自由液面,横摇阻尼较小时,在较小的外部激励力矩的作用下就有可能出现混沌运动。破损船横摇过程中,外部条件的微小变化就可能改变横摇的运动形式,尤其可能出现横摇振幅突然增大的危险情况,必须加以重视。
[1]Pu Jinyun,Cheng Xiaohong,Zhou Renbin.Theoretic analyses and experimental study in nonlinear rolling motion of a flooded ship in waves[M].Process in Safety Science and Technology,Beijing:Science Press,2002:81-86.
[2]来 翔.用胞映射方法讨论一类MKdV方程全局吸引域[J].山东大学学报(工学版),2006,36(1):87-92.
[3]刘 辉,浦金云,陈晓洪.基于胞映射法的破损进水船非线性横摇运动[J].华中科技大学学报(自然科学版),2009,31(8):116-119.
[4]Virgin L N,Begley C J.Grazing bifurcations and basins of attraction in an impact-friction oscillator[J].Physica D,1999,130:43-57.
[5]唐 巍,李殿璞,陈学允.混沌理论及其应用研究[M].北京:电力系统自动化,2001.
[6]浦金云.破损进水舰船横摇特性研究[D].武汉:海军工程大学,2003,108-114.
[7]浦金云,张纬康,陈晓洪等.具有淹水舱的舰船横摇运动建模探讨[J].船舶力学,2007,11(1):47-54.
[8]Murashige S.Chaotic roll motion of a flooded ship in regular beam waves[C]//4th Proceedings of the Experimental Chaos Conference.USA:Florride,1997:349-354.
[9]刘 辉,浦金云,吴向君.破损进水船非线性横摇系统的数值仿真研究[J].武汉理工大学学报(交通科学与工程版),2010,34(4):734-738.
[10]Murashige,Aihara.Experimental study of chaotic motion of a flooded ship in waves[J].Proc.R.Soc.Land,1998,454:2537-2553.
Experimental study in nonlinear rolling motion of a flooded ship
PU Jin-yun,LIU Hui,WU Xiang-jun,CHEN Xiao-hong
(Ship and Power Eng.College,Naval Univ.of Engineering,Wuhan 430033,China)
Through designing nonlinear rolling motion experiment of a flooded ship,a series of rolling experiments of ship model with different states of fixed frequency and fixed wave height is carried out.Then the change rule of ship rolling motion hydrodynamics character following rolling frequency and scope is discussed,and the hydrodynamics character with typeⅡand typeⅢflooded compartment is analyzed.The identify technique of chaos signal is applied to analyze chaos characteristic of flooded ship rolling motion,and validate simulation results,and forecast the breadth ferquency and phase frequency response of flooded ship in regular wave.
rolling motion;flooded ship;chaos;response
U661.3
A
1007-7294(2011)05-0480-09
2010-11-25
武器装备科研项目基金(200805060202)
浦金云(1961-),男,教授,博导,研究方向为舰艇安全性研究。

