高温发汗自润滑技术及其理论研究*
刘佐民 王砚军 张一兵 燕松山 解 芳 冯雪梅 杨丽颖 郭 红 卢 平
刘佐民 硕士 教授 430070 湖北省 武汉市 武汉理工大学 摩擦学研究所 Liuzm98@263.net
王砚军 博士 副教授 430070 湖北省 武汉市 武汉理工大学 摩擦学研究所 wyj64721@sina.com
张一兵 博士 副教授 430070 湖北省 武汉市 武汉理工大学 摩擦学研究所 yibzhang@sohu.com
燕松山 博士 讲师 430070 湖北省 武汉市 武汉理工大学 摩擦学研究所 yansongshan@tom.com
解 芳 博士 副教授 430070 湖北省 武汉市 武汉理工大学 摩擦学研究所 xiefang811222@163.com
冯雪梅 博士 副教授 430070 湖北省 武汉市 武汉理工大学 摩擦学研究所 feng_xumei@163.com
杨丽颖 博士 教授 430070 湖北省 武汉市 武汉理工大学 摩擦学研究所 eo_yangly@ujn.edu.cn
郭 红 博士 高级工程师 430070 湖北省 武汉市 武汉理工大学 摩擦学研究所 Lucky2000402@126.com
卢 平 博士 博士后研究人员 430070 湖北省 武汉市 武汉理工大学 摩擦学研究所 luping1979@gmail.com
1 引言
润滑工程(Lubricating Engineering)是研究减少相对运动物体间摩擦磨损、提高效率、增加产品可靠性和寿命,降低安全隐患的工程科学。
传统上,液体润滑是减磨的普适性方法[1]。随着工业技术(特别是军工技术和航空技术)的发展,固体润滑剂在润滑工程应用领域受到高度重视[2]。20世纪50年代初,MoS2固体润滑剂甚至成为美国的国家军事机密,并专门为其制定了军用技术标准。
近年来,随着航空、航天、海洋开发等高端技术,以及先进制造技术的迅速发展,迫切需要解决极端条件下(如高载荷、高加速度、高真空、超低温、强辐射,以及各种强外场作用)的机械润滑问题[3]。为此,润滑工程从材料结构、制备技术、润滑体分子结构与性能的互耦性到摩擦状态转化、润滑原理及润滑控制等多方面对固体润滑技术开展了广泛研究,并取得了长足进展。在这些研究中,材料结构及其制备技术始终是贯穿固体润滑技术创新的主题,作为学科高度交叉的一个研究领域,仿生润滑(Bionic Lubrication)成为了研究热点。
仿生润滑通过研究并模仿生物系统的功能结构、动作性状及行为机理,为润滑设计提供了全新的学科思维。例如,基于仿生学原理设计的铝活塞-铸铁汽缸套摩擦副仿生表面结构,大幅度地提高了摩擦副的贮油及油膜形成能力[4];基于粉末配比连续变化法制备的PbCO3铁基孔隙梯度自润滑轴承,成功地解决了传统均质含油轴承承载能力低和PV极限值小的问题,延长了轴承的使用寿命[5];采用“仿生关节囊”设计的人工关节润滑系统,提高了人工关节的耐磨性和抗疲劳性[6]。
近年来开展的仿生润滑,例如基于水生动物(如鳝鱼(Monopterus Albus)和泥鳅(Loach),等等)体表滑液减阻机理的仿生润滑[7];基于蚯蚓体表液减粘脱土机理的仿生润滑[8],基于鲨鱼皮表面的盾形鳞片肋条结构的船体表面织构仿生减阻设计[9],以及基于人体汗腺结构及发汗原理的仿生润滑[10],等等,极大地促进了材料科学与生物科学的学科交叉。这些仿生润滑研究的共同特点是采用人工方式重构生物体的胞体结构及其润滑液,以实现其类生物润滑特性。
仿生润滑的载体与生物体存在很大差异,从仿生润滑液到载体结构形态都有大量的理论问题需要探索。特别是仿生润滑材料结构体系的构建、仿生润滑体对摩擦环境的适应性,以及仿生体的润滑自补偿问题。
1973年,Dowson等学者[11]在定义生物摩擦学(Biotribology)范畴时指出:凡是与生物系统相关的摩擦学问题都属于生物摩擦学的研究范畴。
目前已开展的仿生润滑仍然是基于天然生物系统内部器官和外部表皮组织特有的生物润滑特性进行材料构建及其摩擦学环境适应性研究。例如,心脏(Heart)和血管(Blood Vessel)中血液的流动和冲蚀[12-13],滑液关节的润滑机理[14],骨骼(Bones)的多孔状结构、应力集中及软膜润滑特性[15],蚯蚓(Earthworm)体表的润滑性[16-17],壁虎(Gecko)趾底刚毛的动态吸附性[18],以及鸟类(Birds)翅膀形状和羽毛结构的减阻机理研究,等等。人们力图使生物体特殊结构与功能拓宽到工业应用领域,从结构设计、材料制备、润滑设计,以及表面处理等方面实现仿生润滑和减磨的工程效果。
人体汗腺结构(Sweat Gland,SG)是简单的弯曲管状腺体,由分泌部(secretion part)和导管部(duct part)等两部分组成。分泌部由单层柱状上皮细胞围成管状,盘曲成团;导管部是由二三层低柱状细胞围成管道,经真皮向表皮蜿蜒上行,穿越表皮,在皮肤表皮表面形成汗孔(见图1(a))。当环境温度达到30 ℃时,汗腺分泌汗液,排出部分水和离子,经导管部排泄到皮肤表面,能湿润皮肤,有助于调节体温和水盐平衡。
高温发汗自润滑材料(High Temperature Sweating Self-Lubricating Composite,HTSSLC)是基于SG及其发汗机理(Sweating Mechanism),在制备出具有汗腺式微孔结构(Gland-Like Porous Structure,GLPS)基体的基础上,通过向微孔中二次熔渗固体润滑剂而形成的新型高温自润滑材料。由此,笔者构建了HTSSLC制备路径。
【step1】 以TiH2+CaCO3为复合造孔剂,采用液-固相烧结工艺,制备出具有相互贯通有序微孔结构的金属陶瓷硬基体。
【step2】 采用熔渗工艺向基体微孔中加入软金属复合润滑体,在基体表层形成一定深度的润滑层,制成HTSSLC(见图1(b))。
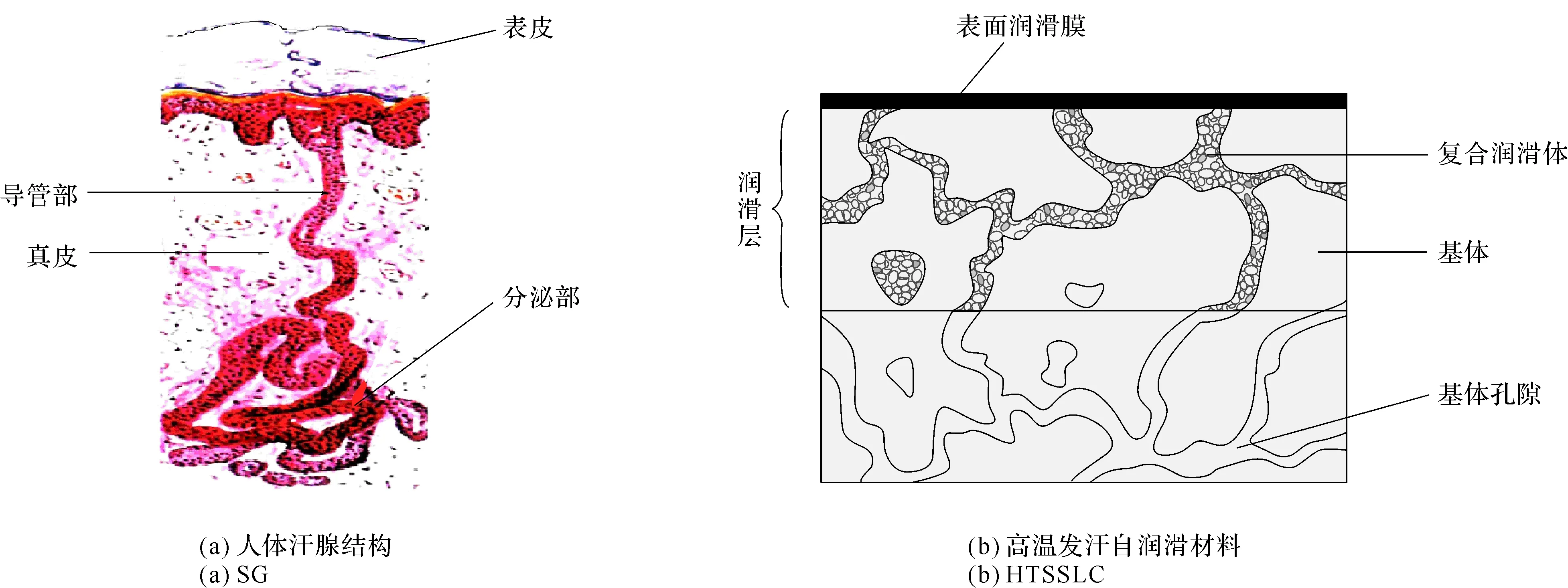
图1 人体汗腺结构及高温发汗自润滑材料结构示意
HTSSLC具有独特的润滑特性,主要体现在两个方面。
【润滑特性之一】 HTSSLC由具有胞体结构的微孔基体(porous matrix)(胞壁(cellular wall))和存储在微孔中的润滑体(lubricant)(胞核(cellular nucleus))组成,由于润滑体热膨胀系数远大于基体热膨胀系数,从而使得润滑体中润滑元素可在高温摩擦热-应力作用下沿着基体中的有序微孔(ordered pores)(胞管(cellular tube))析出,并富集于作用表面形成润滑膜,达到高温发汗自润滑的功能。
【润滑特性之二】 胞核中的润滑元素在高温摩擦-热应力驱动作用下沿着胞管析出,由于严重摩擦部位往往承受较高的摩擦热-应力,因此该接触区的润滑元素析出量将远超出轻微擦伤部位——即擦伤越严重的部位润滑元素析出量越多,从机理上实现了摩擦过程的选择性自补偿润滑。
显然,这种自补偿润滑方式不仅在摩擦过程中对高温重载工况下的摩擦表面提供自补偿润滑剂(元素),而且可对其严重擦伤部位进行动态修复,从而大幅度地提高了摩擦副的可靠性和寿命水平。
HTSSLC的结构及其润滑原理仿生于人体皮肤汗腺结构及其发汗原理,其材料制备技术有别于传统的混元法(elements blend method),涉及多孔材料的制备及软金属的熔浸;其润滑机理也有别于传统的固体润滑,涉及润滑体与微孔基体间的润湿性、润滑元素的扩散性及其润滑相的热物理性能;其摩擦接触有别于均质材料的摩擦接触,而涉及胞体材料的接触强度及多胞体的接触稳定性问题。而这些问题的解决需要材料科学、接触力学与摩擦学的学科交叉。
武汉理工大学刘佐民研究团队在中国国家自然科学基金及中国教育部博士学科点专项基金的共同资助下,通过数理建模和科学试验,解决了胞体结构及其强韧性、微孔基体设计及制备、润滑体设计及复合等关键技术;制备出了HTSSLC,并对其机械性能、润滑特性、润滑机理及其控制进行了系统研究,构建了高温发汗自润滑技术体系(见图2)。本文旨在提出高温发汗自润滑技术体系的理论体系和工程框架。

图2 高温发汗自润滑技术及其理论框架结构
2 高温发汗自润滑材料结构形态的仿生设计及其制备
摩擦学设计的对象是机器系统中的摩擦副,设计内容包括零件的表面形貌及工况参数设计、摩擦副材料润滑设计,以及零件表面(亚表面)的显微组织设计(结构、成分和理化性能)等3个方面。通过复合材料的组元设计、孔隙结构的仿生设计和摩擦学设计,制备高温发汗自润滑材料(HTSSLC),是希望在摩擦过程中借助于高温扩散作用、毛细管束作用和摩擦应力场作用,在摩擦表面形成润滑膜,产生高温减摩及高温自润滑等效果,实现高温自润滑材料的强度、韧性及自润滑性能的统一。
虽然在材料基体的制备过程中,可以通过优化制备工艺获得连续硬质相并控制其孔隙度,获得高强韧性,但HTSSLC的基体体系仍属多孔材料,孔结构形态和分布特征对接触强度影响很大。
本研究团队基于人体汗腺结构(SG)构建的特征材料孔结构由具有汗腺式微孔结构(GLPS)的基体和具有高温扩散性能的润滑体等两部分组成。作为储存固体润滑体的载体,GLPS的基体在具有为润滑元素高温扩散提供通道的同时,本身还应具有优良的耐磨性能。
在HTSSLC基体胞体结构强韧性研究的基础上,根据SGLS的特征和排汗机理,通过结构和功能的模拟,建立GLPS基体的仿生孔隙形态模型,研究其制备工艺。
2.1 结构设计的基本约定
传统多孔材料的研究表明[19],材料的抗拉强度随孔隙度的增加而降低,当孔隙度控制在0%~30%范围内时,存在如下关系。
σ=σ0exp-Boψ
(1)
式中,σ为粉末冶金材料抗拉强度,MPa;σ0为致密材料的抗拉强度,MPa;ψ为总孔隙度,%,其材料方法采用液体静力平衡法(liquid static balance)[20];Bo为取决于材料制造和实验条件的系数,一般为4~7。
基于式(1)及结合HTSSLC的结构特征及功能要求,HTSSLC基体结构——GLPS的设计,需要进行以下基本约定。
【约定1】 颗粒粒级尽可能窄,形状为球形或近似球形。
【约定2】 在成形和烧结过程中,粉末颗粒的体积不变。
【约定3】 球形颗粒受压后形状改变为椭球体,但变形前后颗粒体积相等。
【约定4】 压坯烧结过程中不产生收缩或仅产生微量收缩,压坯烧结过程中孔隙度和孔隙尺寸尽可能保持不变。
【约定5】 制备过程中,烧结体孔隙度控制在15%~30%[20],孔径分布曲线(pore size distribution)服从瑞利分布(Rayleigh Distribution,RD)。
2.2 汗腺式微孔结构数学模型
2.2.1 孔隙结构的数学描述
图3为HTSSLC基体的圆柱体试样及其表面孔隙结构的扫描电子显微镜(SEM)照片。

图3 HTSSLC基体及其有序孔结构
基于上述基本约定及烧结体汗腺式微孔结构(见图3)形态,假设汗腺式微孔的孔径分布近似于瑞利分布(RD),则
(2)
式中,f(r)为GLPS的孔径分布函数;r为随机变量孔半径取值;μo为r的均值。
用极大似然估计法(Maximum Likelihood Estimation Method,MLEM)计算r和μ的极大似然估计量,其似然函数
(3)
式中,L(r)为圆柱孔长度分布函数。
(4)
式中,ri为离散微孔半径。
假设在烧结体内不同圆柱孔的长度分布是连续的,且L(r)近似于对数正态分布(Logarithmic Normal Distribution,LND),基于Kuczynski模型[21]及GLPS的基本约定[22],可得
(5)

由此,得到在r~r+dr之间的变径圆柱孔隙总长度

(6)
GLPS烧结体中的颗粒尺寸与平均孔径之间的关系可用Zener关系[23]类比。
(7)

【定义1孔隙度ψ】 单位体积内的孔隙体积
(8)

由式(7),可得
(9)
由式(3),知
(10)
式中,n为微孔总数。
联立式(1),式(9)和式(10),即得汗腺式微孔结构(GLPS)的汗腺式微孔分布表征模型(Pore Size Distribution Model,PSDM)
(11)
GLPS烧结体孔隙大小和孔隙周围颗粒尺寸都有一定的分布范围。因此,三维气孔的配位数nc(一个气孔周围紧邻的颗粒数目)可以和气孔孔径、包围该气孔的颗粒粒径相联系。
设
(12)

βd值的大小反映了烧结体的致密化程度。一定颗粒堆积条件下,βd可与其理论密度ρ0和烧结密度ρ相联系。
设每个堆积单元体内气孔数为np,含有颗粒数为ns,则有
(13)
即
(14)
由此,得
(15)
规定
(16)
式中,k′为总气孔数与颗粒数之比,对简单立方堆积,k′=1。
2.2.3 比例常数ko
比例常数ko是与粉末粒度、压坯成形压力、烧结温度和烧结时间相关的系数。由Zener关系模型,烧结体的晶粒尺寸与烧结过程中晶粒的生长方式有关。对于汗腺式微孔烧结体,由于可在粉末压坯中添加一定体积分数的复合造孔剂,将烧结体孔隙度控制在15%~30%,故而烧结后烧结体的收缩很小。考虑到孔洞收缩的同时晶粒长大,则孔隙度可近似如下。

(17)
联立式(9)和式(17),得
(18)

令
(19)
式中,B为被移走球冠高度与颗粒平均直径的比值。
可得[24]
(20)
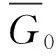
联立式(15)~式(20),可得
(21)
(22)


(23)
式中,γss为固/固界面张力(能),N·m-1(J·m-2);γsg为固/气界面张力(能),N·m-1(J·m-2)。
随着烧结的进行,粉末颗粒间的固-固界面不断增加,而固-气界面不断减少,整个系统的自由能必然是界面能的函数,当系统自由能达到最低状态时,即达到所谓烧结终点。烧结达到终点时,系统的自由能不再变化,则有如下情况[26]。
对于简单立方堆积(Simple Cubic Stack,SCS)
(24)
对于体心立方堆积(Body-Centered Cubic Stack,BCCS)
(25)
对于面心立方堆积(Face-Centred Cubic Stack,FCCS)
(26)


表1 粉末颗粒接触面的增大与有关因素的关系[26]
基于假设条件,GLPS的表征数学模型(式(11))中粉末颗粒的假设是简单立方堆积(SCS)。此时其空隙所占体积分数为48%[26]。在致密化烧结过程中,每个颗粒的配位数(即接触面数)由6推进为18(次配位数)。从几何观点来看,当粉末颗粒以SCS时,要获取最大烧结密度的临界条件为B=0.333,γss/γsg=1.355,Φ=98.3°,此时烧结体内残存的封闭气孔率为1.8%。
HTSSLC的基体——汗腺式微孔体胞结构——在满足一定孔隙度要求的前提下,还需要保证高的强韧性和耐磨性。在本研究中,烧结体孔隙度要通过控制添加复合造孔剂的量来实现,而烧结度按烧结致密化的工艺参数来确定。因此在烧结体孔隙度和孔径分布计算机模拟计算时,取B=0.333,γss/γsg=1.355,Φ=98.3°。
2.2.4 模型验证
基于汗腺式微孔体胞结构模型(Gland-like Porous Cell Structure Model,GLPCSM),采用Matlab.对TiC-Cr-W-Mo-V系和Al2O3-Ni-Cr-Mo-Si系粉末冶金烧结而成的汗腺式微孔体胞结构的孔隙结构及孔径分布进行计算机模拟仿真。


表2 TiC-Cr-W-Mo-V系和Al2O3-Ni-Cr-Mo-Si系试样的孔结构参数
[注] 理论计算时,采用粉末颗粒的简单立方堆积表达式,其空隙所占体积分数为48%[26];取最大烧结密度的临界条件为P= 0.333,γss/γsg=1.355,Φ=96.3°。
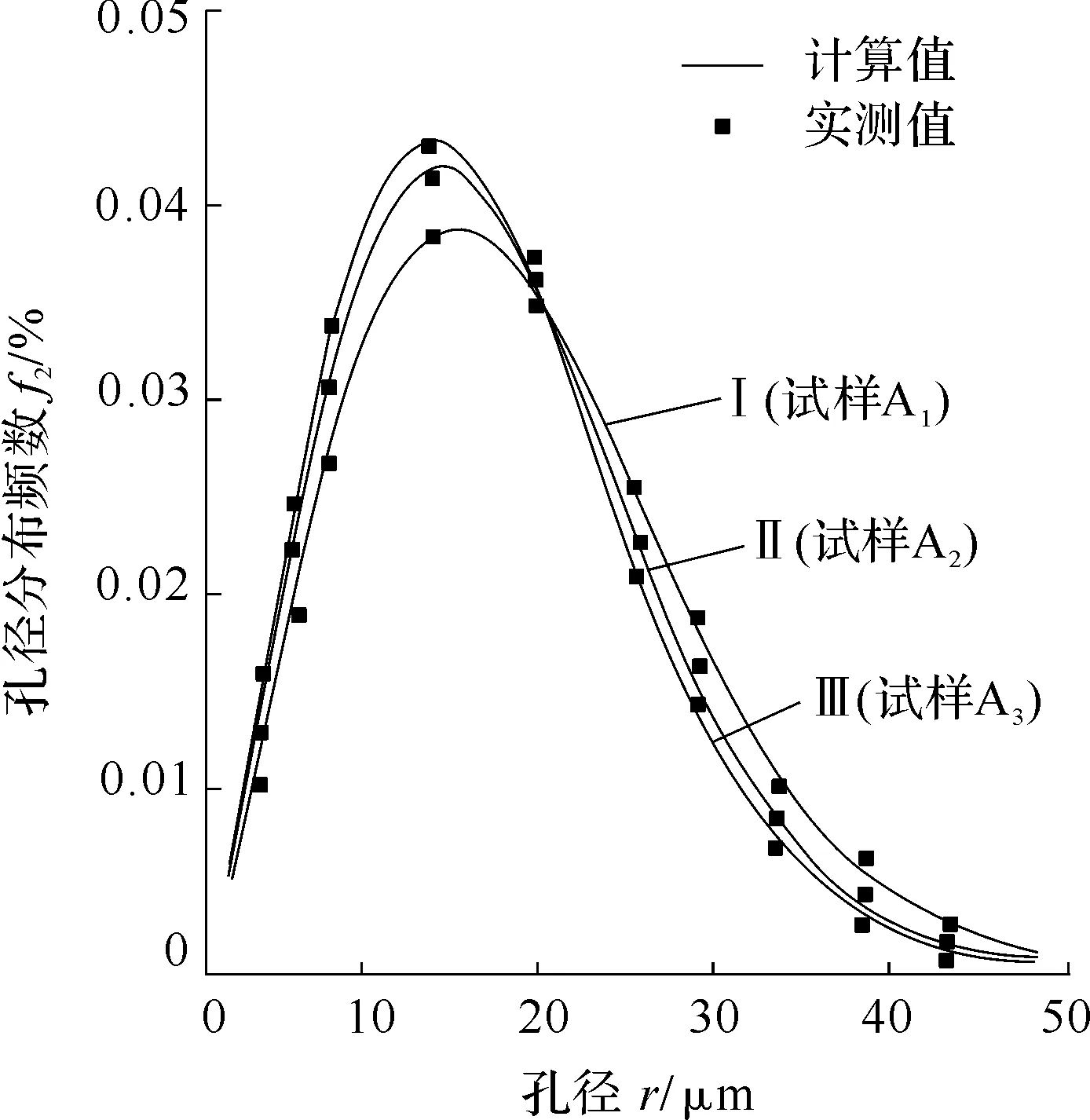
图4 TiC-Cr-W-Mo-V系材料在不同烧结温度下孔径分布的试验值和计算值比较曲线

图5 Al2O3-Ni-Cr-Mo-Si系材料在不同烧结温度下孔径分布的试验值和计算值比较曲线
由表2,图4和图5可以看出,根据模型计算得出的平均孔径及孔径分布与实验基本符合,反映了孔隙分布的变化特性。说明孔隙的长度分布是连续的,孔径分布近似于瑞利分布。由于瑞利分布峰值左侧上升较快,右侧下降缓慢;遵从瑞利分布规律的孔径分布有利于浸渍用固体润滑介质类型、粒度的选择,以增加烧结体中孔隙填充率。
表2,图4和图5还表明,随烧结温度升高,烧结体孔隙度明显减小,且开口孔隙度较总孔隙度下降幅度要大。同时,随着烧结温度升高,烧结体平均孔径变小,孔径分布曲线的峰值增大,而孔径分布区间相应减小。汗腺式微孔结构(GLPS)烧结体孔径分布函数(式(11))能较好地描述微孔金属陶瓷烧结体孔隙结构和孔径分布情况。
理论分析和实验结果的一致性表明,汗腺式微孔结构(GLPS)烧结体孔径分布函数较好地描述了粉末粒度、造孔剂含量、成型压力、烧结温度对烧结体孔隙度、孔隙结构、尺寸及其分布的影响,可用来指导该体系材料的组分设计和制备工艺;GLPS烧结体孔结构形态及其分布规律可通过生胚压制工艺、材料参数选择和烧结工艺参数进行控制;孔径的瑞利分布规律则为设计孔隙中被填充物(固体润滑剂)的粒度选择提供依据。
2.3 HTSSLC基体制备及其性能表征
HTSSLC的体系典型特征是硬质相高强有序微孔基体与具体软质相填充固体润滑剂的复合。为了实现硬质基体的高耐磨性及其在高温下微孔中软质润滑元素的自润滑功能,基体微孔必须具有特殊的结构形态。因此,获取具有高耐磨性能、高强韧的汗腺微孔结构特征的金属陶瓷基体成为制备HTSSLC的关键。
2.3.1 汗腺式微孔烧结成型机理
孔隙度是汗腺式微孔金属陶瓷烧结体的重要特征量,其值与材料组分、粒度、粉粒形态和制备工艺有关,在烧结过程中形成的孔隙主要是所添加造孔剂在溶解、蒸发或分解后所产生的,因此造孔剂对烧结制品的孔隙度、孔隙形状、孔径分布和孔隙贯通性显得非常重要。
在粉末冶金材料制备过程中,由于压坯工艺的需要,在压坯颗粒间设置润滑添加剂,润滑添加剂的烧结挥发使烧结体中形成孔隙,但此类孔隙很小,属“间隙孔”,不是制备工艺设计要求生成的孔隙——“生成孔”。
生成孔的大小和形态与加入的造孔剂(Pore Forming Agents,PFA)有关。为了生成GLPS,本研究团队基于二次造孔法(Double Stage Pore-Forming Technique,DSP-FT),采用添加TiH2-CaCO3复合造孔剂促成生成汗腺式微孔。
【第一次造孔】 TiH2产生H2和Ti;H2逸出,促使粉末颗粒移动和重排,在烧结体内形成初始孔隙,活性很强的Ti起活化烧结的作用;同时压坯成形时挤进间隙孔周围颗粒之间的润滑添加剂分解,在初始孔隙壁上形成生成孔,与间隙孔一同将各初始孔隙连通(见图6)。
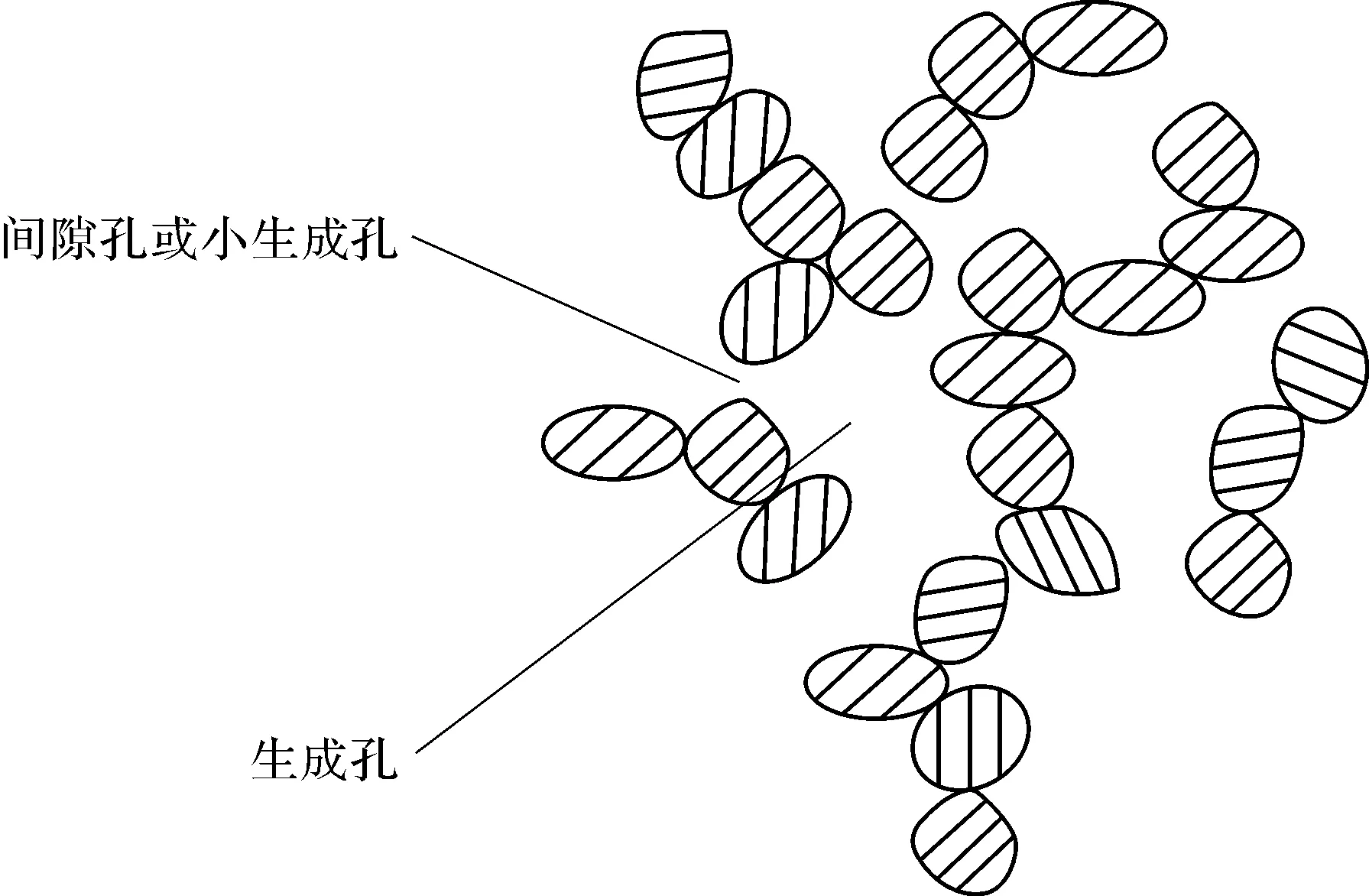
图6 内贯通微的烧结过程模型
【第二次造孔】 CaCO3在比TiH2更高的温度下开始分解,放出CO2气体;由于CaCO3的分解是在烧结体液相逐步形成的温度范围内进行的,可在液相状态下形成气孔通道,并与间隙孔混合击穿烧结硬质相,在烧结体表面形成开口孔。
显然,生成孔的孔结构形态不仅与造孔剂有关,还与压坯工艺所添加的润滑剂有关。
若将复合造孔剂(Compound Pore-Forming Agents,CP-FA)称为硬造孔剂(Hard Pore-Forming Agents,HP-FA),润滑添加剂(Lubricating Agents,LA)称为软造孔剂(Soft Pore-Forming Agents,SP-FA),则造孔剂的颗粒大小、体积分数与孔壁厚度及基体颗粒直径间有如下近似关系[27]。
(27)
式中,Np为以基体颗粒直径为单位的孔隙壁厚度,Np≥1;Dbase为基体颗粒直径,μm;Dhard为硬造孔剂颗粒直径,μm;Vhard为硬造孔剂占有的体积百分数,vol%;Vsoft为软造孔剂占有的体积百分数,vol%。
令
δp=Np·Dbase
(28)
式中,δp为孔隙壁厚度,μm。
由式(27)可以看出,要提高汗腺式微孔烧结体的结构强度,当基体颗粒直径、硬造孔剂(HP-FA)颗粒直径及其添加体积分数一定时,可以通过增加软造孔剂(SP-FA)的体积分数而使N值增大。
压坯内的TiH2分解,形成生成孔时,除了受烧结炉内炉气压力的作用外,还受粉末颗粒间界面张力和孔隙表面张力的作用,而界面张力对孔隙产生的压力较孔隙表面张力小得多,可以忽略不计。因此,生成孔的形成必须满足如下条件。
(29)
式中,PH2为孔隙中氢气压力,Pa;Pg为炉内压力,Pa;γs为生成孔的表面能,N·m-1(J·m-2);r为孔隙半径,m。
根据理想气体压强模型
PH2·VH2=Nmol·R·T
(30)
式中,VH2为单位时间内TiH2分解释放出的H2体积,m3;Nmol为H2的摩尔分子数,mol;R为气体常数,Pa·m3·mol-1·K-1;T为绝对温度,K。
联立式(29)和式(30),得
(31)
式(31)反映了在烧结过程中,真空度与单位时间内造孔剂释放气体体积之间的关系,故此,式(31)可用以指导烧结过程的真空度控制范围。
上述孔隙成型过程表明:GLPS中的汗腺式微孔的形成是在烧结过程中完成的,其成孔机理是基于造孔剂TiH2与CaCO3的分解温度不同。
造孔剂TiH2和CaCO3,及其混合体的热重分析(Thermogravimetric Analysis)和差热分析(Differential Thermal Analysis)的测试实验表明[22]:
(1) TiH2在389~646 ℃之间仅产生微量的失重(weight loss),在646~722 ℃之间出现明显的质量变化,表明TiH2在该温度段内分解而释放出H2;
(2) 随着加热温度升高,CaCO3吸附的水分逐渐挥发,至630 ℃时产生2.29%的质量损失,之后CaCO3开始分解释放CO2,至786.9 ℃时产生了近44%的失重,这表明CaCO3在温度630~786.9 ℃范围内开始分解,并随温度的升高至1 165 ℃而呈现第二次失重,CaCO3在787~1 165 ℃温度范围内出现4次失重过程。
显然,与采用TiH2或CaCO3作为造孔剂相比,采用由TiH2+CaCO3组成的复合造孔剂可使烧结体在400~1187℃范围内,通过造孔剂多次分解而在烧结体中形成具有内贯通和表面开口有序的GLPS。
2.3.2 复合造孔剂组分设计
基于上述研究,GLPS的孔隙度可通过材料配比和工艺参数控制,而孔隙度形态则应当通过复合造孔剂(CP-FA)的比例来实现*孔隙度中的质量采用液体静力平衡法测量。。在GLPS中,典型的孔结构形态应满足如下关系。
ψ>ψ0
(32)
式中,ψ为总孔隙度,%;ψ0为开口孔隙度,%。
(33)
式中,ρ为烧结体的密度,g·cm-3;ρ0为与烧结体同一组成物质的理论密度,g·cm-3。
(34)
式中,mA为试样在空气中的质量,g;mB为试样在蒸馏水中煮沸2 h后,在空气中的质量,g;mC为试样在蒸馏水中煮沸2 h后悬挂于水中的质量,g;mE为悬挂的丝与筐在水中的质量(皮重),g。
由此,ψ是理论密度的余数(例如,理论密度为85%的烧结体,其孔隙度为15%),反映了孔隙容积所占烧结体的百分率;ψ表征的孔隙如同人体汗腺一样,呈伸展到表面的互通网络状。ψ0作为烧结体的表面开口孔隙度,表征了高温发汗材料基体内固体润滑剂析出的通道。因此,总孔隙度与开口孔隙度之比
kp=ψ0/ψ
(35)
是GLPS材料的重要参数。
图7为不同造孔剂及其含量对金属陶瓷烧结体总孔隙度与开口孔隙度之比kp的变化曲线。
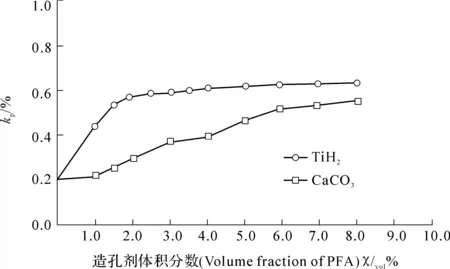
图7 不同造孔剂与含量对烧结体kp的影响
由图7可看出,采用TiH2造孔剂获得的kp值明显地高于由CaCO3造孔剂制备出烧结体的kp值。研究表明[22],kp值的影响因素除了造孔剂含量外,造孔剂分解温度范围也是重要因素。对于在较高温度下分解的CaCO3造孔剂而言,分解过程中形成孔形态呈现球形,而在较低温度下分解的TiH2造孔剂形成的孔则呈现非规则形态。显然,不规则孔隙较之球形孔隙具有高的比表面能,易于互相贯通,但球形孔则具有高的强度和良好的孔径可控性。
【推论1】 为了制备出理想的GLPS,必须采用复合造孔剂,应平衡单体造孔剂对烧结体中孔隙形态的影响。
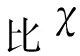

图8 复合造孔剂TiH2+CaCO3对kp的影响

【推论2】 在总孔隙度一定的情况下,复合造孔剂造孔的烧结体,其kp明显地高于单体造孔剂TiH2或CaCO3制备出的烧结体。
图9为添加单体造孔剂(Monomer Pore-Forming Agents,MPFA)和复合造孔剂(Compound Pore-Forming Agents,CPFA)时金属陶瓷烧结体的微孔结构SEM形貌。

图9 金属陶瓷烧结体在单体造孔剂和复合造孔剂条件下的微孔结构形态(SEM照片)
由图9(a)可以看出,添加单体造孔剂TiH2时,烧结体生成孔为不规则形态;由图9(b)可以看出,添加单体造孔剂CaCO3时,生成的孔形状近似于规则的圆形。对比图9(a)和图9(b),可以发现,采用单体造孔剂TiH2所得的孔隙贯通性远比单体造孔剂CaCO3的高,这证实采用TiH2造孔剂制备的烧结体,其kp值比采用CaCO3造孔剂制备出的烧结体的高。由图9(c)可以看出,采用合理比例的复合造孔剂TiH2+CaCO3时,可制备出具有理想kp值的内贯通的规则微孔。
作为HTSSLC,除了具有足够的孔隙度为固体润滑剂提供载体外,高温和高接触强度性能也非常重要。为此,在造孔剂组分设计中,需要添加Al2O3作为弥散质点,这使得材料在烧结过程中,TiH2和CaCO3在分解时释放出的H2(气态)和CO2(气态)将受到弥散分布的且有惰性的Al2O3质点阻隔,防止气孔通道过分收缩和封闭,从而形成孔隙孔径差别比较小,形状较规则的内部互贯通与表面有序规律分布的微孔结构。
2.3.3 基体材料组分设计
由于金属陶瓷中硬质陶瓷相和金属相间物理、化学性能的互匹配性对界面应力及整个材料性能有很大影响,因而基体组分设计时应充分考虑各相间弹性模量和热膨胀系数的匹配性、各相间的化学反应性,以及各相间的互润湿性,并以此为原则,通过添加剂改善其组分间的互适应性。
组分设计中采用的主要组元有(Ta,Nb)C,WC,Mo2C,VC等碳化物硬相;TaC,NbC,TiC,Cr2C3等高合金强韧相;Ni,Co,Cu,Fe,Mo,Cr等金属粘结剂;TiH2,CaCO3及其复合物等高温造孔剂。
对于GLPS金属陶瓷烧结体,可采用微孔结构特征(孔隙度、孔径、孔径分布、孔道形貌,等等)作为评价指标,分析造孔剂类型、添加量对孔隙结构特征的影响,实现复合造孔剂配比的优化。
基于金属陶瓷的烧结温度和造孔剂的分解温度范围,在制备中,选用复合形态的无机造孔剂(TiH2/CaCO3/TiH2+CaCO3),并将其按给定比例与Fe-Cr-W-Mo-V合金及TiC基材(见表3)进行混合。混合中添加一定量的Al2O3惰性弥散质点及1vol%的润滑剂,并在球磨4 h后在300~700 MPa压力下冷压成型。成型后在0.01~0.1 Pa真空环境下进行真空液相烧结,烧结温度为1 200~1 250 ℃,保温60 min后随炉冷却至室温。

表3 基材组分
为了提高基体强韧性,在其组分中添加了微量稀土元素,由于稀土元素在微孔结构金属陶瓷的硬质相内与界面处发生偏析,形成氧化物和硫化物,起到了净化界面的作用,使晶粒长大的驱动力减小而限制了晶粒的长大,从而有效地细化了组织,粘结相相对于硬质相的润湿性改善,提高粘结相/硬质相界面的结合强度,增加材料的韧性。
研究表明,在开口孔隙度控制在15%~20%情况下,以TiH2+CaCO3作为复合造孔剂,于1 240 ℃保温60 min烧结制备TiC/CrMoWV系高温发汗自润滑金属陶瓷烧结体时,基体中添加0.7%的Y2O3,硬度可提高2~3个单位,压溃强度可提高15%左右;基体中添加一定量的Co(约为TiC含量的10vol%)可明显提高烧结体的强韧性,同时加入这两种成分,增强增韧效果更明显。其力学性能测试结果见表4。

表4 Y2O3和Co对自润滑耐磨金属陶瓷烧结体力学性能的影响
2.3.4 汗腺式微孔基体制备工艺设计
GLPS高温自润滑烧结体是由合金粉末、陶瓷粉末、添加剂和造孔剂等多种粉末混合在一起烧结而成,这些组元在密度、粒度及颗粒形状方面差别很大。为了获得表层孔隙分布均匀有序、内部孔隙互相贯通、且具有高耐磨性和高强韧性的烧结体,制备工艺是极其重要的技术环节。
图10为基于球磨混合方法的GLPS金属陶瓷烧结体制备工艺流程。球磨混合采用干粉机械混合工艺,其筛分过程按组分粒度进行,冷压成型采用双面加压,加压过程中缓慢增加压力,并设定保压时间,以保证气体的排除及制品的压实。烧制在真空炉中进行,设定升温速度、烧成温度、保温时间和冷却速度等参数。

图10 GLPS金属陶瓷烧结体工艺流程
GLPS烧结体既要求有一定的贯通孔隙度,又要求具有高的耐磨性和高的强韧性。在基体粉末颗粒粒度均一的情况下,烧结体孔隙度取决于等径颗粒的堆积方式和造孔剂的添加量;为使烧结体的尺寸尽可能与毛坯尺寸相近,可基于烧结体各组分的熔点,通过严格控制烧结温度而控制粉末颗粒的长大程度。按液相烧结理论及工艺试验情况,考虑主要基体材料的熔点或分解温度(见表5),设计其烧结温度范围为1 200~1 250 ℃。

表5 主要基体材料组分熔点或分解温度
研究表明,在600~1 000 ℃范围内,复合造孔剂可实现二次分解,在其较低温度下分解的气体可使烧结体中生成内贯通微孔。而在较高温度下分解的气体则使烧结体表面生成有序微孔(开口孔)。与此同时,合金中的碳化物与金属粘胶剂发生共晶反应可生成部分液相,降低了TiC及FeCrWMoV混合粉末的烧结温度并拓宽了其烧结温度范围,使烧结体内在保留了一定贯通孔隙度的同时又能形成高强韧性的烧结颈(见图11)。

图11 GLPS烧结体孔隙结构形态
2.3.5 汗腺式烧结体性能影响因素分析
HTSSLC制备技术的关键是在于控制烧结体的孔隙度、孔隙贯通性,以及孔隙的形状、结构、尺寸和孔径分布,并保证其具有足够的强韧性和耐磨性。
孔隙度和孔隙的结构特征(孔径、孔径分布和孔隙长度等)会直接影响烧结体的强度、固体润滑剂的含量和分布,继而影响其高温力学性能和自润滑性能。因此,烧结体品质影响因素的分析,对于改善性能和控制工艺稳定性有重要意义。
2.3.5.1 基体陶瓷相组分对孔隙度和力学性能的影响
几乎所有材料组分都对烧结体的孔隙度和力学性能有影响,但就液相烧结过程而言,高熔点陶瓷相(TCC)含量对烧结体本构特征的影响最大。图12和图13分别为在复合造孔剂含量一定的情况下,TCC含量对烧结体的致密化行为、压溃强度、孔隙度及其显微硬度影响的变化曲线。

图12 TCC含量对基体密度和压溃强度的影响

图13 TCC含量对显微硬度和开口孔隙度的影响
由图12和图13可以看出:
(1) 致密化程度随TCC含量的增加而减小,且对材料的压溃强度影响很大;压溃强度随TCC含量的增加而减小,当TCC含量超过20%时,压溃强度急剧减小;
(2) 显微硬度随TCC含量的增加而提高,但当TCC含量超过15%时,显微硬度随TCC含量的增加而下降,TCC含量超过20%时,显微硬度急剧下降;
(3) 开口孔隙度随TiC含量的增加而提高,在TCC含量不变的情况下,材料的孔隙度随造孔剂含量的增加而增加;
(4) 强度和硬度随造孔剂含量的增加而降低。其原因是陶瓷相熔点较高,在烧结过程中影响了与被熔融材料间的润湿性。
综合考虑TCC含量对烧结体孔隙度及力学性能的影响,在该材料体系中,15%~20%的TCC含量较为合理。
2.3.5.2 粉末粒度和成形压力对孔隙结构影响
表6列出了的不同粒度基体粉末及成形压力对烧结后汗腺式微孔金属陶瓷基体物理机械性能的影响。

表6 金属陶瓷烧结体的物理机械性能
[注1] 表中每一烧结工艺取3个试样进行测量,然后取其平均值;
[注2] 表中的密度采用液体静力平衡法测量[20]。
由表6可看出:
(1) 基体粉末粒径的增大将降低基体的密度和压溃强度,但增大了基体的开口孔隙度,从而提高了基体储存润滑介质的能力;
(2) 成形压力越大,基体密度和压溃强度越大,而开口孔隙度越低。
因此,调整设计粉末粒度和成形压力可获得不同机械性能和孔隙度特征的材料基体。
图14为不同成形压力下(基体粉末粒度为55~73 μm)的金属陶瓷烧结体孔径分布曲线。
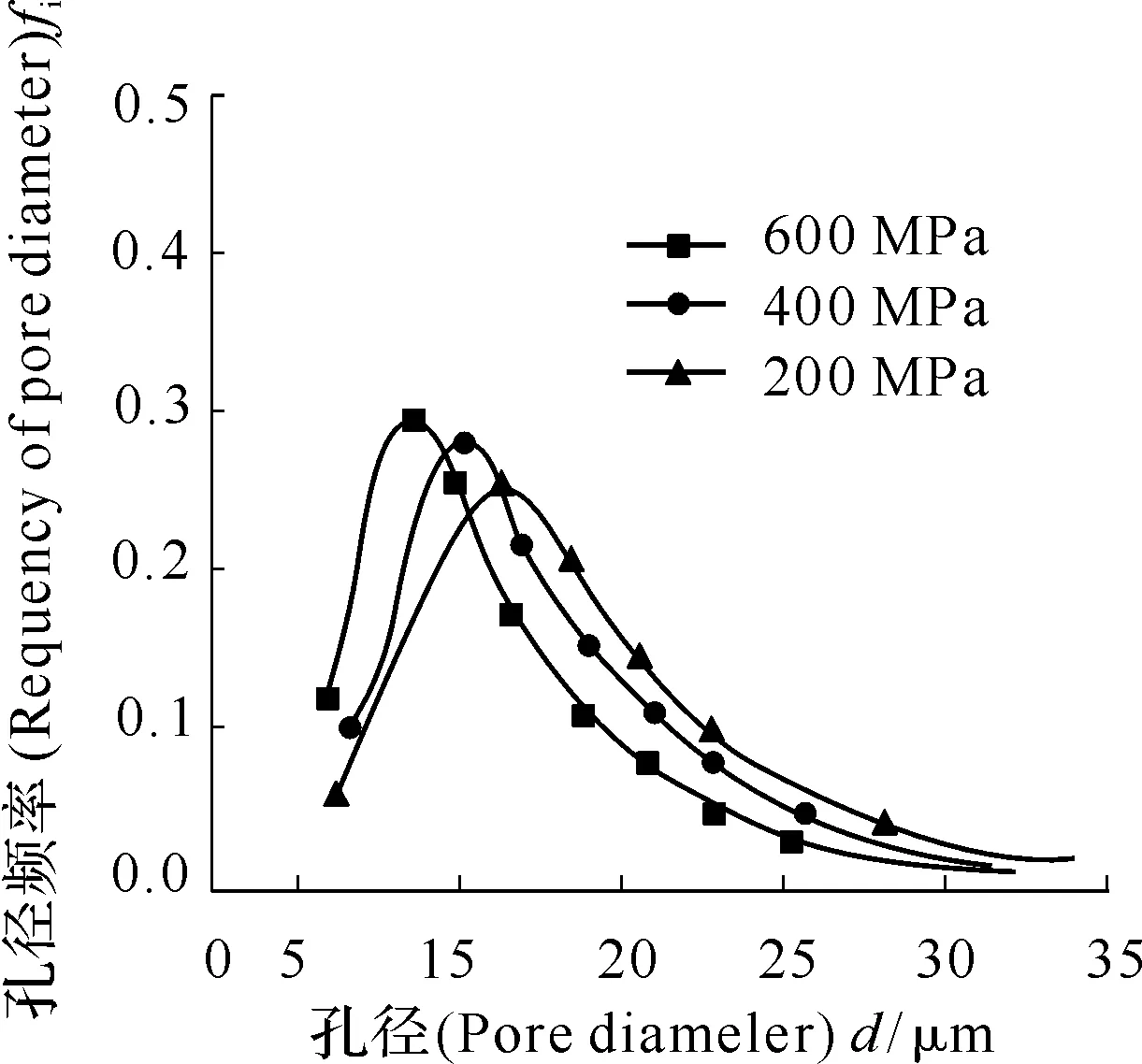
图14 成形压力对烧结体孔径分布的影响
由图14可以看出:
(1) 在不同的成形压力下,烧结体都具有峰值左侧上升较快,右侧下降缓慢的特征;
(2) 随着成形压力的增大,孔径分布曲线的峰值增大且曲线左移,表明成形压力增大使烧结体中小孔径孔隙的比例稍有增大,大孔径孔隙的比例略微降低。
进一步的理论研究表明,孔径分布特征服从瑞利分布(RD)。孔径分布的这种特征为基体微孔中固体润滑剂的粒度和填充率控制提供了理论依据。
图15给出了粉末粒度和成形压力对于TiC/FeCrWMoV系金属陶瓷烧结体孔隙度的影响曲线。
图15 粉末粒度和成形压力对烧结体开口孔隙度的影响
从图15可以看出:
(1) 随着成形压力的增大,烧结体的开口孔隙度逐渐减小。在成形压力增至500 MPa后,开口孔隙度的变化逐渐平缓,但不同粒度粉末制备的烧结体开口孔隙度下降的程度不同,粉末越细,成形压力对烧结体开口孔隙度的影响越小*因为粉末松装时,颗粒间形成较多的空隙,施加压力后,首先是这些空隙被填充,颗粒间发生移动而重新排列,压坯密度提高,空隙变小。;
(2) 随成形压力进一步提高,颗粒间达到紧密堆积后在接触处开始变形以增加接触面积,同时颗粒因变形而发生加工硬化使变形过程发生困难;
(3) 在成形压力达到一定数值后,压坯密度随成形压力的升高变化很小,烧结体的开口孔隙度基本保持不变。
综合考虑基体粉末粒度和成形压力对烧结体孔径分布和孔隙度的影响,同时考虑烧结体的力学性能,汗腺式高温自润滑烧结体的制备过程中,成形压力选用600 MPa。
图16给出了粉末粒度和成形压力对TiC/FeCrWMoV系金属陶瓷烧结体孔隙结构的影响曲线。

图16 粉末粒度和成形压力对烧结体孔结构形态的影响
从图16可看出,粉末粒度对孔径频率分布的影响很大,这是由于细粉末颗粒具有较高的松装密度,颗粒间形成的空隙尺寸小,且细粉末颗粒具有大的比表面积和高的比表面能,因而烧结性能好,烧结体的收缩率也大。因此,随着基体粉末粒径的减小,烧结体的孔径尺寸和孔隙度都减小,且孔径分布区间变窄。
综合考虑基体粉末粒度和成形压力对烧结体孔径分布和孔隙度的影响,同时考虑烧结体的力学性能,汗腺式高温自润滑烧结体的制备成形压力应控制在600 MPa。基体粉末粒度可根据被熔浸的固体润滑介质性能对孔径结构参数的要求进行选择。
2.3.5.3 烧结温度、烧结时间对孔结构和力学性能的影响
图17是粒度为55~73 μm的基体粉末在600 MPa压力下成形烧结后金属陶瓷基体孔隙度和孔径随温度变化的关系曲线。图17表明,随烧结温度的升高,烧结体的孔隙度逐渐减小,且开口孔隙度较总孔隙度下降幅度略大。同时,随着烧结温度的升高,烧结体的最大孔径减小,但平均孔径变大,孔径分布曲线的峰值和孔径分布区间也相应减小。

图17 烧结温度对烧结体孔隙度的影响
图18为烧结温度对金属陶瓷烧结体孔径分布的影响。由图18可看出,随着烧结温度的升高,烧结体的最大孔径减小,但平均孔径变大,孔径分布曲线的峰值和孔径分布区间也相应减小。

图18 烧结温度对烧结体孔径分布的影响
显然,烧结温度升高,加快了各组元间物质的扩散速度,使粉末的活性增强,促进颗粒间烧结颈的形成和长大,导致烧结体进一步收缩,孔隙度降低;另一方面,随着烧结温度的升高,烧结体内液相含量增加,使粉末颗粒处于润湿状态;颗粒间的每一孔隙都成为毛细管,无数毛细管的作用使颗粒发生位移和重新排列而互相靠拢,增大了接触面积,减少了比表面能;孔隙变化趋向于表面积减小,从而使小孔隙进一步减小直至消失,平均孔径变大且趋于均一。
图19给出了烧结时间对烧结体孔隙度的影响曲线。由图19可以看出,烧结初期,随烧结时间的延长,烧结体孔隙度急剧减小,当烧结一定时间致使烧结体烧透时,孔隙度变化趋于平缓。烧结时间与烧结温度有关,烧结温度高时,烧结时间短;相烧结温度低时,烧结时间长,其中温度是烧结的主要因素。对于汗腺式微孔烧结体,为保证其具有足够的力学性能和一定的孔隙度,在压坯烧透的前提下,烧结时间可适当减小。
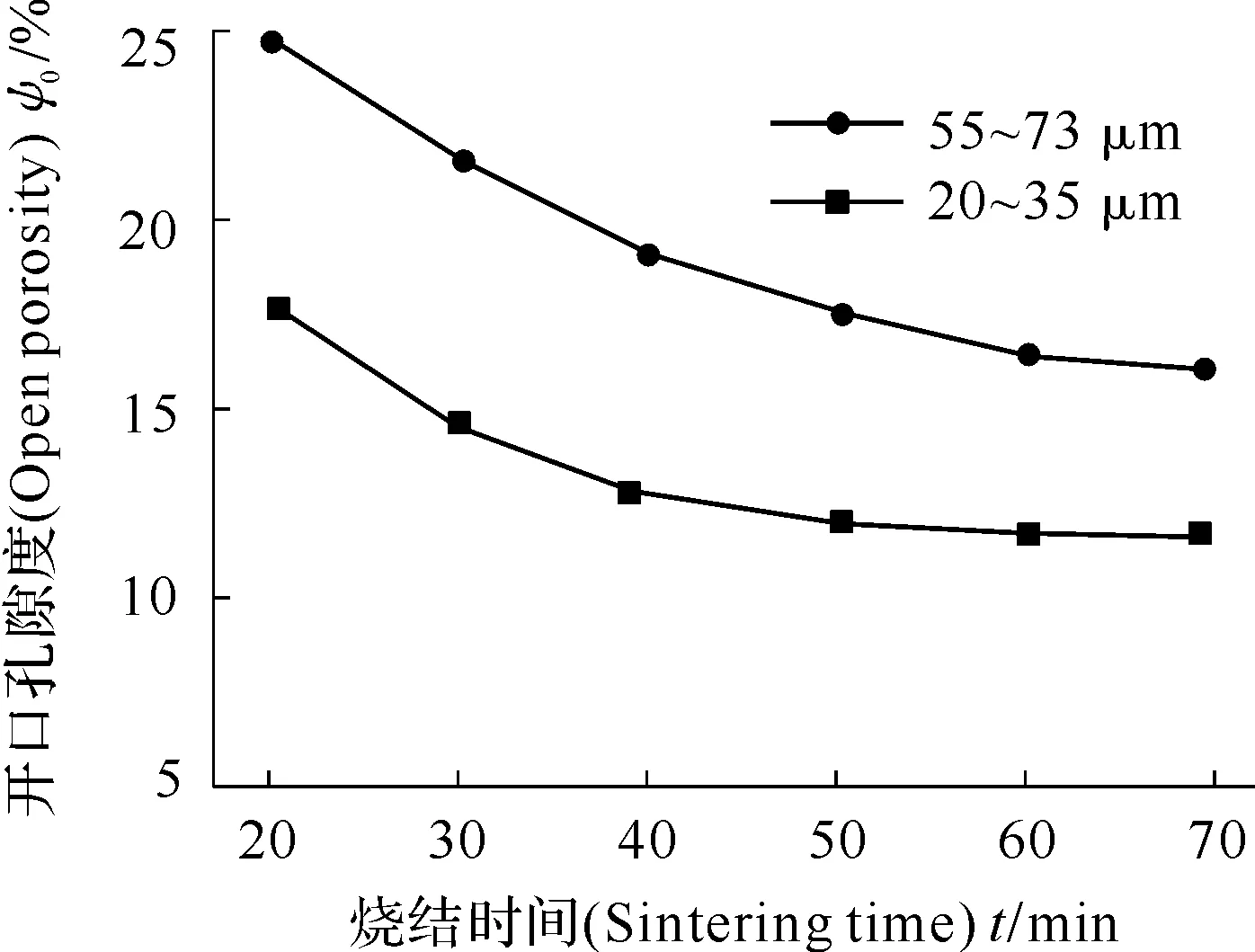
图19 烧结时间对烧结体开口孔隙度ψ0的影响
图20给出了烧结体显微硬度和压溃强度随烧结温度的变化曲线。由图20可知,随烧结温度的升高,烧结体的显微硬度和压溃强度提高,且压溃强度较显微硬度提高的幅度大。当烧结温度为1 230 ℃时,压溃强度较低温烧结时显著提高。此后,随着温度的继续升高,烧结体的显微硬度和压溃强度缓慢增加。由此表明,在一定的烧成温度下,烧结体具有相应的孔隙度;烧成温度提高,烧结体趋于致密,开口孔隙度减小。在有液相参与烧成的条件下,粉末颗粒的位移和重新排列遵循最小能量原则,经过球磨混料处理的颗粒表面具有较高的比表面能,烧成温度越高形成的液相量越多,其粘滞流动和表面张力的拉紧作用使其填充于孔隙中,促使晶粒重排,互相靠拢以增大接触面积,减小比表面能,从而使烧结体孔隙度降低,致密度和压溃强度提高;因此,对高强韧性的烧结体而言,严格控制其烧结温度显得非常重要。
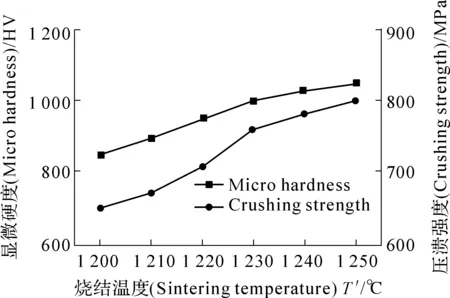
图20 烧结温度对烧结体显微硬度和压溃强度的影响
2.3.5.4 孔隙度对烧结体压溃强度和轴向收缩率的影响
图21为粉末粒度为55~73 μm,成形压力600 MPa,真空烧结后GLPS金属陶瓷烧结体的压溃强度和轴向收缩率随其孔隙度变化的关系曲线。

图21 孔隙度对烧结体的压溃强度和轴向收缩率的影响
由图21可知,烧结体的压溃强度和轴向压缩率都随孔隙度的增加而降低,当孔隙度超过某一数值时,压溃强度和轴向压缩率都随孔隙度的变化趋于平缓。这与常规粉末冶金材料的压溃强度随其孔隙度的增加而按指数下降[28]的规律不同;其原因是GLPS金属陶瓷基体受外部压应力时,应力在颗粒之间的粘结颈处集中,材料的强度主要取决于颈部强度。GLPS金属陶瓷基体采用真空瞬时液相烧结,颗粒粘结颈处积聚一定的液相量,冷却后颗粒间的颈部变粗,此时颈部强度的增强作用大于孔隙度对压溃强度的削弱作用;因此,GLPS金属陶瓷基体的强度主要取决于烧结颈的强度。
3 汗腺式微孔结构(GLPS)材料的接触力学及其强韧性研究
由于高温发汗自润滑材料(HTSSLC)的基体存在微孔,将导致应力集中,从而影响其接触应力状态分布,局部高接触应力还将诱发疲劳裂纹,甚至引起脆性断裂[29]。为了提高HTSSLC基体的接触强度,本研究团队基于基体所具有的厚壁多孔结构形态,引入描述孔结构特征的特征参数λ值,建立描述孔隙度、弹性模量、泊松比之间相互影响关系的理论模型;建立单胞接触应力分析理论模型(Contact Stress Theoretical Analysis Model of Solo-Cell,CSTAM-SC),计算和分析其接触应力(Contact Stress)和孔穴应力集中(Stress Concentration),为工艺设计和工况环境适应性预测提供理论基础。
3.1 GLPS的表征
3.1.1 汗腺式有序孔结构几何表征模型(Ordered Porous Structure Geometric Model,OPSGM)
由图3可以看出,HTSSLC的基体表面分布着有序微孔,其孔隙度较低且分布比较均匀,孔径差别不是很大,形状也比较规则。
尽管HTSSLC基体——GLPS的微孔结构与蜂窝材料类似,然而,二者最大的区别在于,蜂窝材料的孔隙度较大(通常高于70%),胞壁很薄;而为了承担足够高的载荷,GLPS的孔隙度较小(通常低于20%),胞壁较厚。薄壁孔结构的材料结构分析所采用的应力和应变横臂梁模型(Cross-Beam Model,CBM)不适用于厚壁结构孔结构的材料结构的应力应变分析,特别是接触强度分析。
基于HTSSLC基体GLPS所具有的多孔微观形貌特征,进行如下假设。
【假设1】 孔洞为均匀分布。
【假设2】 孔洞为边数相同、大小相等的正多边形。
【假设3】 孔洞的壁厚均匀且各向同性。
基于上述假设,可将HTSSLC分割成为理想的多胞结构(Multi-Cellular Structural,MCS),为了讨论孔结构形态对材料接触强度的影响,将HTSSLC基体构建出3种几何模型(见图22),而不使材料特征参数失真,讨论中,应用统一的数学表达式对模型结构进行描述,以使其讨论结果拓宽应用于一般的均质有序孔结构材料中。
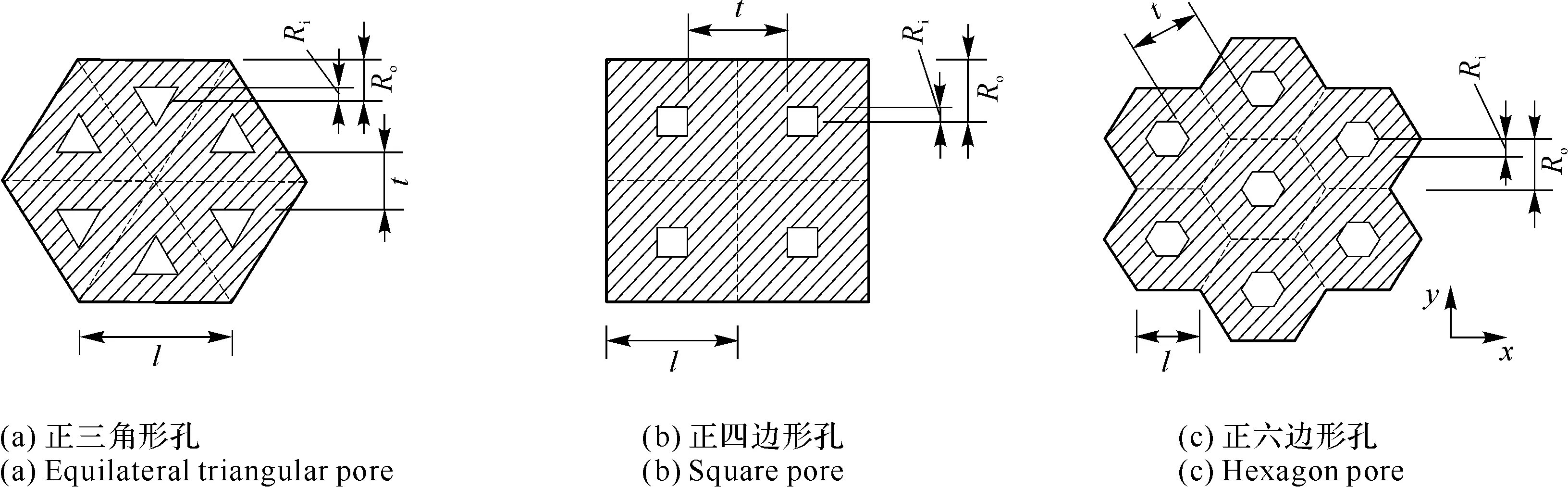
图22 HTSSLC胞体结构几何模型
【规定1】 MCS由结构参数完全相同的基础胞元(Base Cell,BC)组成。
若BC由胞孔和完整的胞壁组成,则可通过材料结构特征值(Material Structural Eigenvalue,MSE)表征BC。
(36)
式中,λ为材料结构特征值(MSE),0<λ<1;Ri为正多边形胞孔的内切圆半径;Ro为基础胞元正多边形外壁的内切圆半径。
由正多边形面积公式,可以推导出正多边形多胞体的胞孔总面积
(37)
式中,N为基础胞元的个数;n为正多边形基础胞元的边数。
同理,也可以推导出正多边形多胞体的总面积。
(38)
式中,So为正多边形多胞体的总面积。
由式(36)~式(38)可以推导出正多边形多胞体结构的相对密度(relative density)。
(39)
式中,ρ*为胞体密度;ρs为胞壁材料密度。
正多边形多胞体结构的孔隙度(porosity)
(40)
壁厚
t=2(Ro-Ri)
(41)
接触长度(contact length)
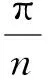
(42)
壁厚与接触长度之比
(43)
由式(43),可得
(44)
将式(44)代入式(39),可得
(45)
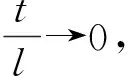
(46)
胞体结构的孔隙度也可简化表述如下。
(47)
式(39)和式(40)适用于任意厚度的胞体结构,而式(46)和式(47)仅适用于薄壁胞体结构。由此可知,无论胞壁厚度如何,任意正多边形多胞体的相对密度和孔隙度均只与其材料结构特征值λ有关,而与正多边形的边数n无关,即与正多边形胞孔的形状无关。式(46)可计算任意正多边形薄壁胞体的相对密度,并将Gibson等学者[30]对不同正多边形蜂窝材料相对密度的计算作为特例包括在内。
本研究团队建立的OPSGM,其针对的对象属于厚壁均质结构。本文将具有宽适用域的式(39)和式(40)称为相对密度和孔隙度广义表达式(Generalized Expression,GE),将较窄适用域的式(46)和式(47)称为相对密度和孔隙度狭义表达式(Special Expression,SE)。
由GE和SE可以分别计算出相对密度和孔隙度与材料结构特征值之间的关系(见图23)。

图23 孔隙度和相对密度与特征参数的关系
由图23可以看出,随着λ的增大,GE计算的材料孔隙度(或相对密度)呈幂函数增大(或减小)趋势,而SE计算的孔隙度(或相对密度)则呈线性增大(或减小)趋势。当λ趋近于1时,如λ≥0.9,即胞壁很薄时,GE计算的孔隙度(或相对密度)与SE计算的孔隙度(或相对密度)几乎相等,误差小于5%,此时可以用SE近似计算孔隙度和相对密度;相反地,当λ→0时,即胞壁很厚时,SE计算的孔隙度(或相对密度)与GE计算的孔隙度(或相对密度)相差较大,此时只能用GE计算厚壁均质有序孔材料的孔隙度和相对密度。将引入特征值λ建立的SE和GE与Gibson/Ashby模型进行对比(见表7)。

表7 引入特征值λ建立的SE,GE与Gibson/Ashby模型[30]对比
由图23可以得出以下推论。
【推论3】 当λ<0.4时,胞体的孔隙度和相对密度均变化缓慢,且两者的变化率均在8%以内,此时可以将材料看成连续介质体。
【推论4】 当λ>0.4时,孔隙度增大的速率变快,相对密度减小的速率也变快,且孔隙度和相对密度的变化率都较大,从11%(对应于λ=0.5)迅速增加到48%(对应于λ=0.9)。
3.1.2GLPS胞体结构特征参数λ对其力学性能的影响
3.1.2.1 弹性模量
弹性模量(modulus of elasticity)是胞体材料的重要力学指标,用于衡量材料产生弹性变形的难易程度。厚壁胞体材料的整体弹性模量(effective modulus of elasticity)不但与构成胞壁材料的力学性能有关,而且与其结构参数有关。
对于厚壁均质正六边形胞体理论模型(Theoretical Model of Homogeneity Thick Wall Regular Hexagon Cell,TM-HTWRH),借助正六边形微孔结构弹性模量表达式[30],可得
(48a)
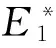
相对弹性模量(relative modulus of elasticity)
(48b)
将式(43)代入式(48),并取n=6,可以得到以材料结构特征值λ表征的厚壁均质有序孔结构材料弹性模量
(49a)
材料相对弹性模量
(49b)
将胞体材料的材料结构特征值λ与孔隙度ψ0的关系(见式(40))带入式(49),可以得到材料的弹性模量、相对弹性模量与孔隙度的关系模型。
(50a)
(50b)
式(49)和式(50)表明,当基体材料一定(μs与Es为定值)且胞体形状为正六边形时,其弹性模量只与材料结构特征值λ或孔隙度ψ有关。
图24为厚壁均质有序孔材料的相对弹性模量与材料结构特征值λ及孔隙度ψ之间的关系曲线(令μs=0.3)。

图24 相对弹性模量与材料结构特征值和孔隙度的关系曲线
由图24可以得出以下推论。
【推论5】 材料的相对弹性模量随着λ的增大呈线性减小趋势,且在λ=0.8处出现拐点。
【推论6】 当λ>0.8时,相对弹性模量减小的速率变慢。
【推论7】 随着ψ的增大,相对弹性模量呈幂指数减小趋势,当ψ<0.2时,胞体材料的整体弹性模量达到构成胞壁材料的30%以上。
3.1.2.2 泊松比
正六边形微孔结构材料的泊松比[30]可以表述为如下形式。
(51)
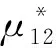
将式(43)代入式(51),并取n=6,可得
(52)
由此可以得到泊松比与孔隙度的关系。
(53)
图25为厚壁均质有序孔材料的泊松比μ*与材料结构特征值λ及孔隙度ψ之间的关系曲线(令μs=0.3)。
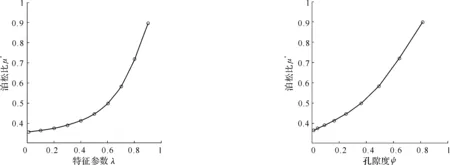
图25 泊松比与材料结构特征值和孔隙度的关系曲线
由图25可知,随着特征参数λ和孔隙度ψ的增大,材料的泊松比逐渐增大。
【推论8】 当λ<0.4或ψ<0.16时,材料泊松比的增长速率比较缓慢,变化率小于6%。
【推论9】 当λ>0.4或ψ>0.16时,材料泊松比的增长速率明显变快,变化率从8.2%(对应于λ=0.5)迅速增加到25.1%(对应于λ=0.9)。
以上的研究表明,采用TM-HTWRHC及其材料结构特征值λ所建立的GLPS的胞体结构材料强度模型(GLPS-Cellular Structure Material Strength Model,GLPS-CSMSM),可用于计算任意正多边形胞体结构的相对密度和孔隙度,其值广义地包括了正多边形蜂窝材料的Gibson/Ashby模型算例。
【规则1】 当λ≥0.9(孔壁很薄)时,可以采用Gibson/Ashby模型(SE)计算材料的相对密度和孔隙度。
【规则2】 当λ≤0.9(孔壁较厚)时,只能采用GE计算材料的相对密度和孔隙度。
【规则3】 当λ<0.4时,材料的相对密度和孔隙度随λ值的增大变化较缓慢,此时可以将该材料看成连续介质体而具有较高的强度。
【规则4】 当ψ<0.2时,厚壁均质有序孔材料的整体弹性模量达到构成胞壁材料的30%以上。
【规则5】 当λ<0.4(即ψ<0.16)时,材料泊松比的增长速率比较缓慢。
【规则6】 当λ>0.4(即ψ>0.16)时,材料泊松比的增长速率明显变快。
3.2 厚壁单胞体接触力学模型
图26为HTSSLC的接触力学结构模型。在宏观法向力P作用下,接触点处将产生反作用力,这将导致接触微区域中的胞元最先产生变形甚至破坏。为了便于分析,提取其接触处的单胞体作为接触强度的基本单元进行研究。
需要说明的是,对于图22建立的正多边形多胞体模型而言,当n→∞时,胞孔和胞壁均演变为圆形,但是圆形的胞壁将导致其接触长度l=0,这与实际情况不符,因此,当胞孔为圆形时,依旧以正六边形分割胞壁,并保证基础胞元(BC)的孔隙度不发生改变(见图26)。

图26 HTSSLC的接触力学结构模型
此外,“无限大板”(infinite plate)中的孤立小圆孔理论(isolated small circular hole theory)指出[31],无论板的几何形状如何,只要孔心离板边的距离大于C·Ri(Ri为小孔半径,C为与材料有关的特征值,按2~2.5取值),且相邻两孔的距离大于2C·Ri,就能按“无限大板”中的孤立小圆孔来处理。此时,板的边缘形状不再重要,可以将其看成圆环处理。据此,如果胞孔中心到胞体边缘的最小距离大于C倍胞孔半径,即当
Ro>CRi
(54)
在视图平面内就可以将其视为“无限大板”中孤立小圆孔而进行分析。此时,HTSSLC单胞体的外壁可以简化处理为圆(见图26中的虚线)。
基于上述分析,本研究团队以空心圆柱型厚壁单胞体为对象,建立厚壁单胞体接触力学模型(Contact Mechanics Model of Thick-Wall Cellular Structure,CMMTWCS)(见图27)。
为了求解厚壁基础胞元的胞体接触力学问题,进行如下假设。
【假设4】 空心与实心胞体结构的轴向长度均为L。
【假设5】 厚壁胞体的孔隙度用式(40)描述。

【假设7】 厚壁胞体在外载荷下处于弹性变形状态,且变形曲线是连续可导的,不存在奇异点。
根据“假设7”,厚壁胞体变形过程可作为曲梁(curved beam)来处理,即厚壁单胞体在外载荷压缩作用下胞壁产生弯曲变形,使其受力后略呈椭圆状,导致接触点附近的曲率半径增大。这样,可先引用等效曲梁(effective curved beam)计算方法求得接触区的实际曲率半径,再将其带入经典Hertz理论,进行接触力学求解。
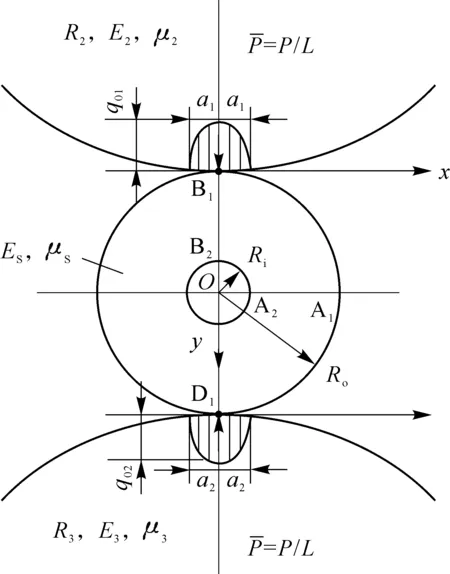
Ro为空心胞体结构的外径;Ri为空心胞体结构的内径;R2为与之相接触的上实心圆柱型胞体的半径;R3为与之相接触的下实心圆柱型胞体的半径;Es为空心胞体胞壁材料的弹性模量;E2为上实心胞体的弹性模量;E3为下实心胞体的弹性模量;μs为空心胞体胞壁材料的泊松比;μ2为上实心胞体材料的泊松比;μ3为下实心胞体材料的泊松比;P为总径向压缩外载荷;a1为上接触区的接触半宽;a2为下接触区的接触半宽;q01为上接触区的最大接触压力;q02为下接触区的最大接触压力。O为空心胞体中心;B1为空心胞体与实心胞体上接触中心;D1为空心胞体与实心胞体下接触中心;A1A2为空心胞体在垂直与水平方向的截面长;B1B2为空心胞体在垂直方向的截面长。
3.3 胞壁等效曲梁计算方法
3.3.1 胞壁等效曲梁的弯曲应力及变形
为了修正接触点处的实际曲率半径,基于空心胞体结构的受力对称性(见图27),截取其1/4胞壁(例如,A1A2B2B1)为研究对象,采用等效曲梁计算方法对其弯曲应力及变形进行分析(见图28)。

图28 胞体结构受力分析
端面B1B2固定,端面A1A2受其垂直力P/2和力矩MA的共同作用,则可得
(55)
式中,FN为作用于端面CC1的力;φ为端面CC1与端面A1A2的夹角。
(56)
式中,M为作用在端面CC1上力矩;MA为作用在端面A1A2上力矩;Ra为胞壁等效曲梁的平均半径,即为弧线oo′半径。nn′为距离轴线oo′为η的层面。
根据胞壁等效曲梁胞体受力分析(见图28),可以得到以下关系。
(57)
(58)
式中,h为胞体二分之一壁厚。
A=L·(Ro-Ri)
(59)
式中,A为胞壁等效曲梁的轴向截面面积。
假设弯曲变形过程中胞壁的厚度恒定,即η为定值,令轴线oo′上某微段的弧长为ds,其对应的圆心角为dφ,则由曲梁定理(Curved Beam Theorems),可得ω和ds。
(60)
式中,ω为dφ的角应变;k为胞壁等效曲梁的截面系数。
(61)
式中,ε0为ds的应变。
(62)
式中,σ为曲梁应力。
假设变形后端面A1A2和B1B2之间不产生角位移,即

(63)
联立式(55),式(56),式(49)和式(63),可得
(64)
(65)
将式(55)和式(56)带入式(60),式(61)和式(62),可得
(66)
(67)
(68)
(69)
3.3.2 胞壁等效曲梁的挠度
在外载荷作用下,胞壁等效曲梁(cellular wall effective curved beam)将产生挠度(deflection)(见图29)。

oo′为胞壁等效曲梁的轴线;oc为轴线上任一点;o′为欲求挠度的点;φ0为过点o作曲梁轴线的法线而形成的与x轴的夹角;φ为过点oc作曲梁轴线的法线而形成的与x轴的夹角;φ1为过点o′作曲梁轴线的法线而形成的与x轴的夹角。

若o′点在x向的位移为u,可得

(70)
若o′点在y向的位移为v,可得

(71)
3.3.3 厚壁胞体结构接触点的实际曲率半径
由曲梁定理可知,胞壁等效曲梁的轴线oo′弯曲变形后的曲率半径
(72)
由于假设胞体的壁厚不发生变化,因此,变形后的胞壁外径
(73)
联立式(66),式(67)和式(73),可得
(74)
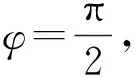
(75)
式(75)还可以表示为如下形式。
(76)
式中,kα为接触点处曲率半径的增大系数,它不仅与胞体结构的几何尺寸有关,还与外载荷的大小有关。
将式(76)带入赫兹接触理论模型(Hertzian Contact Theory Model,HCTM),就可以计算厚壁胞体结构的接触力学特性。当kα=0时,即为HCTM。因此,式(76)拓展了HCTM的适用范围。
3.3.4 厚壁胞体结构的接触力学表征
将接触点处的实际曲率半径带入HCTM[32],可以得到上部接触区和下部接触区的接触半宽(contact half widths)和最大接触压力(maximum contact pressure)。
(77)
式中,a1为上部接触区的接触半宽。
(78)
式中,a2为下部接触区的接触半宽。
(79)
式中,q01为上部接触区的接触压力。
(80)
式中,q02为下部接触区的接触压力。
当R2→∞,R3→∞时,模型变换为厚壁胞体结构与上下两个平面空间半无限体接触,式(77)~式(80)可以写成以下形式。
(81)
(82)
(83)
(84)
上部接触区的接触压力分布(contact pressure distribution)
(85)
下部接触区的接触压力分布
(86)
厚壁胞体结构的总径向位移δ将由上部接触区接触变形引起的径向位移δ1,下部接触区接触变形引起的径向位移δ2,上半部胞壁弯曲变形产生的径向位移δ3和下半部胞壁弯曲变形产生的径向位移δ4等4个部分组成。
δ1和δ2可由HCTM求得[32]。
(87)
(88)
根据图28和图29
x1=y1=Ra
φ0=π/2
φ1=0
(89)
δ3和δ4等于1/4胞体结构在y向的位移(绝对值)(见图28)。将式(89)带入式(71),可得
(90)
因此,厚壁胞体结构总径向位移(general radial displacement)
(91)
基于HCTM,由接触引起的局部应力分布(local stress distribution)
(92)
式中,σx c为由接触引起的x向应力。
(93)
式中,σy c为由接触引起的y向应力。
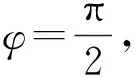
(94)
式中,σx b为由弯曲变形引起的x向应力。
因此,由接触变形和弯曲变形引起的沿x轴方向的总局部应力(general local stress)
(95)
对于平面应变情况,沿z轴方向的局部应力
(96)
式中,σx为接触变形和弯曲变形引起的沿x轴方向的总局部应力。
3.3.5 基于模型的有限元法验证
为了验证胞壁等效曲梁计算方法的精确性,本研究团队借助有限元法分别建立了厚壁胞体结构与上平面和下平面半空间无限体的接触模型,并利用有限元软件(ABAQUS)对其接触特性进行数值分析。
模型参数如下[33],胞体结构几何参数为Ro=15 mm,Lt=15 mm,材料选用H59铜,材料参数为Es=98 GPa,μs=0.3;由于上、下两平面半空间无限体R2→∞,R3→∞,故取其尺寸为30 mm×30 mm,选用不锈钢材料,材料参数为E2=E3=210 GPa,μ2=μ3=0.3。
为了提高计算效率,基于模型的对称性,只建立其1/4接触模型,模型的边界条件如下。
【边界条件1】 位于y轴上的节点在x方向不产生位移。
【边界条件2】 位于胞体水平中心线上的节点在y方向不产生位移。
【边界条件3】 耦合半空间无限体底面上所有节点的y向位移,即令半空间无限体底面上所有节点在y方向产生的位移相同。
【边界条件4】 胞体与半空间无限体的接触表面间没有摩擦。
根据以上参数和边界条件,分别建立了以下两种情况的接触模型。
【模型Ⅰ实心圆柱体接触模型(SolidCylindersContactModel,SCCM)】 孔隙度ψ=0。
【模型Ⅱ厚壁胞体接触模型(ThickWallCellularStructureContactModel,TWCSCM)】 孔隙度ψ=0.1。
选用二维平面应变单元(CPE4I)建模,并对预计接触区域进行网格细分,细分后,两种模型的单元总数分别为4 025和3 295(见图30)。

图30 胞体与半空间无限体的有限元接触模型
此外,建模过程中考察了网格划分的敏感度(sensitivity),将单元总数同时扩大一倍后发现,求解的最大误差均不超过1%,现有的网格划分密度可以满足求解精度问题。
图31为TWCSCM(见图30(b))的有限元算法及基于胞壁等效曲梁计算模型解析算法(见式(81),式(83),式(91)和式(95)),对不同载荷作用下的空心胞体最大接触压力q0、接触半宽a、总径向位移δ和y轴水平应力σx进行的验证性计算与分析情况。结果表明,解析算法和有限元算法的结果具有良好的符合性,从而验证了胞壁等效曲梁计算方法的正确性。
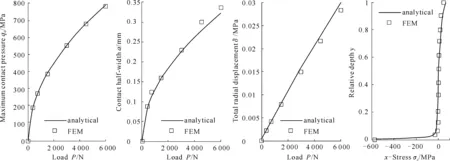
图31 厚壁胞体(ψ=0.1)解析法和有限元法的对比分析结果
3.3.6 基于曲梁模型的厚壁胞体局部应力分析
孔隙度对厚壁胞体接触力学特性的影响不仅反映在接触表面,而且反映在其内部应力分布上。参照图30的坐标系,令
d=y/(2h)
(97)
式中,d为相对深度;y为对称轴y上某点的坐标值;2h为胞体的壁厚。
基于等效曲梁计算模型,可求出具有不同孔隙度胞体在受力变形后y轴上的点沿x向的应力σx与相对深度d的相互关系(见图32)。

图32 不同孔隙度胞体结构y轴上的局部应力σx与相对深度的关系曲线(P=3 000 N)
由图32可知,对具有不同孔隙度的胞体结构而言,其y轴上的x向最大压缩应力均出现在d=0处,说明胞体结构的外表面所受的压应力最大,且压应力的值在靠近外表面处急剧变大;其x向最大拉伸应力均出现在d=1处,说明胞体结构的内孔表面所受的拉应力最大。随着相对深度的增加,x向应力从压应力向拉应力过渡,过渡点大致出现在d=0.5处,即胞壁厚度方向的中间位置。
若将x向最大拉应力和最大压应力随孔隙度的变化关系绘制成曲线(见图33),从图33可以看出,x向局部最大拉伸应力及最大压缩应力均随孔隙度的增大而增大,在孔隙度区间[0,0.1],[0.1,0.2],[0.2,0.5],最大应力的变化速率先大后小再变大。

图33 x向局部最大应力随孔隙度的变化曲线
由此可知,外载荷相同的情况下,孔隙度的增大,将导致胞体内局部应力的增大,这将有可能使胞体在局部应力最大点处产生破坏。
3.4 厚壁胞体接触强度试验
厚壁胞体多孔材料的一个显著特点就是材料的宏观力学性能不仅取决于材料的物理特性,而且还取决于细观孔洞的结构特征。
传统的具有周期性结构的多孔材料,多采用正方形为基础胞元,研究其在单轴压缩(外力为均布载荷)下的宏观力学问题和微观力学问题[34],没有考虑接触应力对其微孔结构的影响。
以高副接触(线或点接触)为应用背景的高强摩擦学多孔材料,其结构强度涉及最大接触应力下的胞体结构稳定性问题。因此,可基于接触力学体系建立其胞体结构的微观变形与整体材料宏观接触载荷之间的联系,研究胞体在接触状态下的宏观变形问题;这种从微观到宏观的接触强度分析特别适用于高副接触零件(如滚柱轴承)的承载能力预测[32,35]。
为了探讨微孔结构形态对厚壁胞体材料接触强度的影响,本研究团队以圆形作为周期性基础胞元,构建了正三角形胞孔厚壁单胞体结构形态模型(Model of Thick Wall Solo-Cell Structure with Regular Triangle Hole,MTWSCS-RTH),正四边形胞孔厚壁单胞体结构形态模型(Model of Thick Wall Solo-Cell Structure with Regular Quadrangle Hole,MTWSCS-RQH),正六边形胞孔厚壁单胞体结构形态模型(Model of Thick Wall Solo-Cell Structure with Regular Hexagon Hole,MTWSCS-RHH),以及圆形胞孔厚壁单胞体结构形态模型(Model of Thick Wall Solo-Cell Structure with Circular Hole,MTWSCS-CH),并建立了统一的形态识别符号Ro(Ro为胞体的外径)和Ri(Ri为正多边形胞孔的内切圆半径)(见图34),且胞体中心与正多边形胞孔的中心重合。由此,可以得到厚壁胞体材料的孔隙度ψ。

图34 试样压缩示意
对于正三角形胞孔厚壁胞体材料,其孔隙度
(98)
对于正四边形胞孔厚壁胞体材料,其孔隙度
(99)
对于正六边形胞孔厚壁胞体材料,其孔隙度
(100)
对于圆形胞孔厚壁胞体材料,其孔隙度
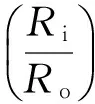
(101)
3.4.1 试验设计
本研究团队选用具有与金属陶瓷相类似的脆韧性但强度较低的H59铜材料,制备了孔隙度为0.1和0.15的单孔圆柱体试样。圆柱体试样的外径为15 mm,各种孔形尺寸参数可由式(98)~式(101)计算得出(见表8)。表中,Nc为对应试样的个数,Lt为圆柱体试样的轴向长度。

表8 试样尺寸参数
实验在YE型数控液压式压力机上进行,分别对各圆柱体试样进行接触压缩试验,试样压缩试验要求见图34。
试样径向受两刚性平面挤压,其中上部刚性平面固定,下部刚性平面受外力P作用,产生的位移记为S。加载方向见图35。其中,图35(a)和图35(b)分别为正三角形孔胞体的正向受力和斜向受力情况,图35(c)和图35(d)分别为正四边形孔胞体的对边受力和对角受力情况;图35(e)和图35(f)分别为正六边形孔胞体的对边受力和对角受力情况;图35(g)为圆形孔胞体受力情况。每项试验重复3次,取其数据平均值作为试验结果,讨论孔结构形态对其接触强度的影响。
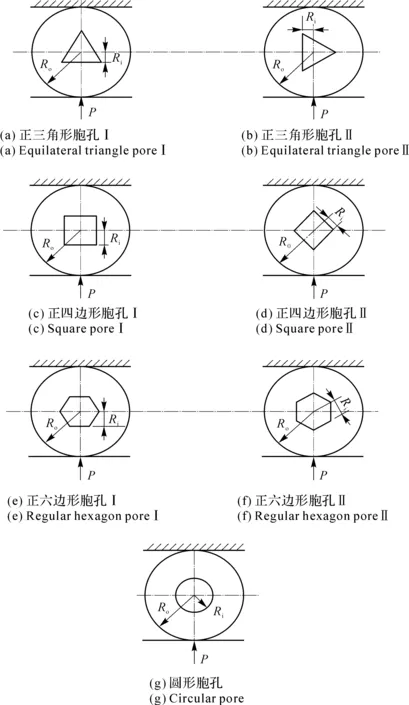
图35 厚壁胞体材料的胞孔结构
3.4.2 厚壁胞体变形与力-位移曲线的关系
图36为典型的厚壁胞体接触条件下的力(P)-位移(S)曲线。P-S曲线分为以下4个区。
【A区初始预紧力区(initialpreloadarea)】 消除试验系统的误差和接触表面粗糙度的影响。
【B区基体弹性变形区(elasticdeformationareaofmatrix)】 局部接触应力只引起基体变形,不对胞孔结构产生影响。
【C区胞孔结构变形区(deformationareaofcellularhole)】 逐渐增大的接触应力已扩展至胞孔边缘,引起胞孔结构的变形,当变形达到一定程度时,便萌生了裂纹,此时对应的临界外力为Fs,称为失效力。
【D区胞体材料失效区(destructionareaofcellularmaterial)】 裂纹不断扩展。

图36 典型的压缩过程P -S曲线
图36给出了以下3组特征值参数。
【力特征值(forceeigenvalue)】 包括初始预紧力Fo,基体弹性变形最大力Ft和胞体接触失效力Fs等3项。
【位移特征值(displacementeigenvalue)】 包括基体弹性变形最大时对应位移St和胞体接触失效位移Ss等2项。
【能量特征值(energyeigenvalue)】 用Wi(i=A,B,C,D)表示P-S曲线所属区的能量特征值,WA为由初始预紧力引起的变形能,WB为由基体弹性变形引起的变形能,WC为由胞孔结构变形引起的变形能,WD为裂纹的扩展能。
根据以上特征值可知,胞体裂纹的形成经历了初始预紧力区、基体弹性变形区和胞孔结构变形区。
3.4.3 孔结构形态对厚壁胞体接触强度的影响
3.4.3.1 孔隙度对接触强度的影响
图37为在ψ=0.1和ψ=0.15等两种孔隙度情况下,各胞体接触压缩时的P-S曲线。
显然,P-S曲线可以很好地反映厚壁胞体材料的接触强度。当P=Fs时,胞体产生裂纹,导致材料失效;Fs越大,对应的裂纹形成能量越大。这说明要使胞体材料产生裂纹则需要做更多的功,即该胞体不容易发生破坏。
图37表明,在失效前,各分图B区的斜率几乎相同,这表明B区为基体的弹性变形区,由于各胞体的基体材质均相同,因此B区斜率与微孔结构形态无关;而当P-S曲线达到一定值时,微孔结构形态对其承载能力的影响才反映出来;试验结果也反映出孔隙度越大,材料的承载能力越低。

图37 胞体孔隙度对接触强度的影响
3.4.3.2 加载方向对接触强度的影响
胞体材料的接触强度不仅与其孔隙度有关,而且受承载方向的影响。本研究团队分析了当孔隙度ψ=0.1时,具有正三角形孔胞体正向受力和斜向受力情况,以及具有正四边形孔胞体和正六边形孔胞体对边受力和对角受力情况,得到加载时的P-S曲线(见图38)。

图38 胞体承载方向对接触强度的影响
结果表明,对于正三角形孔胞体而言,其在正向受力和斜向受力情况下的胞体失效力相差很小;对于正四边形孔胞体和正六边形孔胞体而言,两种承载方向对失效力的影响很大,对边受力情况下的胞体失效力明显大于对角受力情况。因此,对边受力情况下的接触强度优于对角受力情况。这是由于对角受力情况下,孔应力集中区离接触应力区较近,应力干涉作用较强,而对边受力情况下,在裂纹出现之前,垂直于受力方向的两条底边发生弯曲,表现出一定的塑性,从而使对边受力情况下的胞体承载能力明显高于对角受力情况下的胞体承载能力。
3.4.3.3 微孔形状对接触强度的影响
胞体材料的接触强度除了受其孔隙度和承载方向影响以外,还受微孔形状的影响。图39为当孔隙度ψ=0.1时,7种微孔形状对接触强度的影响。比较可知,正六边形孔胞体对边受力情况的接触强度最大,正四边形孔胞体对角受力情况的接触强度最小,而圆形孔胞体的接触强度居中。
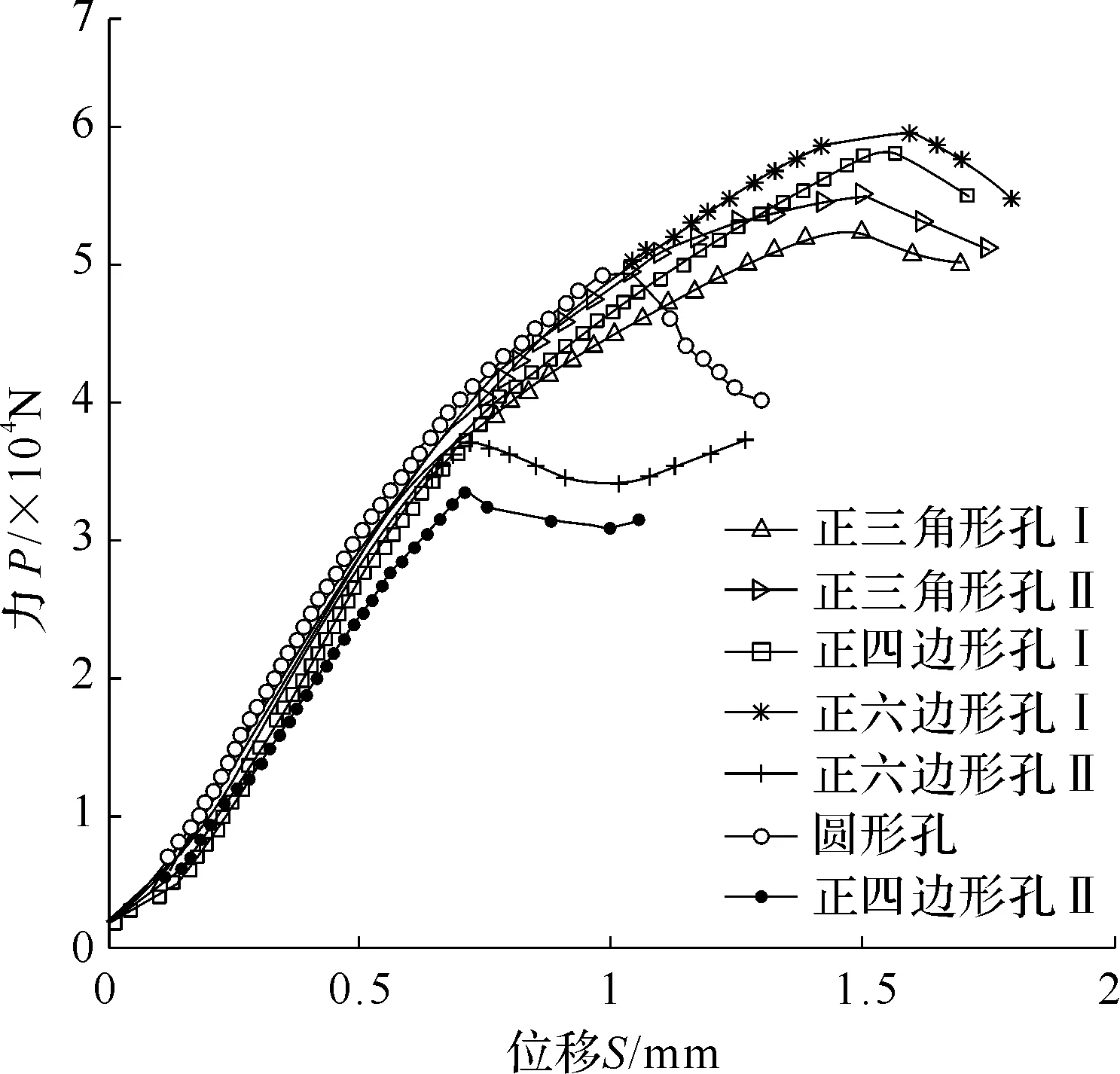
图39 不同形状孔的胞体的P-S曲线
3.4.4 孔结构形态对其裂纹产生及扩展的影响
实验研究了具有不同微孔结构的厚壁胞体在接触力作用下裂纹产生的形式。图40为在相同载荷下不同孔结构的裂纹形态。

图40 试样破坏形貌
由图40可以得出以下推论。
【推论10】 对于正四边形孔胞体Ⅰ和正六边形孔胞体Ⅰ(对边受力情况),其裂纹起源于孔口顶边与底边的中点。
【推论11】 对于正四边形孔胞体Ⅱ和正六边形孔胞体Ⅱ(对角受力情况),其裂纹则起源于孔口与初始接触点紧邻的上、下等两尖角处。
【推论12】 对于圆形孔胞体,其裂纹起源于孔口的上、下两顶点处。
【推论13】 对于正三角形孔胞体Ⅰ(正向受力情况),其裂纹起源于孔口上部尖角处和下底边中点处。
【推论14】 对于正三角形孔胞体Ⅱ(斜向受力情况),其裂纹起源于孔口垂直边的两个尖角处。
这些裂纹产生后都朝着初始接触点方向扩展。值得注意的是,正三角形孔胞体斜向受力时(见图40(a)),其裂纹虽然也是经初始裂纹源向初始接触点扩展,但该方向却不与载荷方向垂直,这与均布外载荷作用下的裂纹扩展形式有很大差别[36],说明非均匀分布的接触力对胞体结构的破坏形式影响很大。因此,胞体结构受到过载接触力作用时,裂纹源均产生在微孔孔口边缘且离初始接触点最近的地方;裂纹朝着初始接触点方向进行扩展,大多数情况下与外载荷加载方向有关。
为了分析不同胞孔结构的厚壁胞体在接触力作用下裂纹产生的原因,本研究团队借助有限元法建立了胞体接触模型(Cellular Structure Contact Model,CSCM),利用ANSYS软件对胞体与刚性平面接触过程中产生的应力进行分析。
为了减少计算量,选用PLANE82,CONTACT172和TARGET169单元,建立二维平面应力接触模型,由材料手册[33]查得H59铜材料的弹性模量E=9.8×104MPa,泊松比μ=0.3,屈服强度σs=200 MPa,剪切模量G=37 692 MPa,无润滑剂时的摩擦因数f=0.45。
以正三角形孔胞体Ⅰ、正四边形孔胞体Ⅰ和正六边形孔胞体Ⅱ为例,通过有限元分析得到胞体最大正号的主应力受力云图(见图41)。

图41 试验结果与有限元结果的对比分析
由图41可知,不同胞孔结构的胞体最大正号的主应力均位于胞孔孔口边缘且离初始接触点最近的地方,这与裂纹源起点的位置完全符合。因此,制备的胞体结构的接触失效行为主要是由最大正号的主应力引起的,说明该材料具有一定的脆性。此外,由试验结果和有限元结果对比可知,裂纹产生后沿着应力梯度变化最快的方向,即初始接触点方向扩展。由此可以得出以下推论。
【推论15】 孔隙度、微孔形状及承载方向均对厚壁胞体结构的接触强度有较大影响,厚壁胞体结构的接触强度随着孔隙度的增大而减小;对边受力情况下的接触强度优于对角受力情况;比较各类孔形,正六边形孔胞体对边受力时的接触强度最大。
【推论16】 对边受力情况下,在裂纹出现之前,垂直于受力方向的两条底边发生弯曲,表现出一定的塑性,从而使该受力情况下的胞体失效应力明显高于对角受力情况下的胞体失效应力。
【推论17】 裂纹源均产生在微孔边缘且离初始接触点最近的地方,裂纹沿着平行于外力的方向进行扩展。
3.5 多孔厚壁胞体的接触稳定性试验研究
HTSSLC基体中含有大量的有序胞孔,胞孔在实现存储固体润滑剂功能的同时,也影响了材料的承载能力。研究表明[34,36],胞孔间的相互作用既可增大应力集中的程度,也可削弱应力集中的程度,其布阵方式对孔洞材料的宏观力学性能影响很大。
然而,已有的研究是针对建筑材料类的均布外载荷,且为圆形孔结构的结构力学状态而展开的,对于以提高摩擦高副接触强度为目的的异形胞体的接触力学稳定性研究尚未见诸报道。
本研究团队在厚壁单胞体孔结构形态对其接触强度影响的基础上,讨论其胞孔相互间的接触稳定性(contact stability)问题,以指导材料制备及其零件工况适应性设计。
为了有效揭示布孔方式及孔距对多孔厚壁胞体接触强度的影响,本研究团队采用H59铜材料分别制备了含等径双孔胞体、三孔胞体及四孔胞体等3组圆柱体试样,其外径Ro均为15 mm,轴向厚度Lt均为15 mm,孔隙度ψ均为0.1,多孔试样的胞孔沿圆柱体横截面呈中心分布,胞孔分布半径为Rd(见图42)。

图42 试样胞孔分布模型
试样在YE型数控压力机上进行接触强度试验。试验按胞孔分布情况(见图42)分别对其进行压缩试验。
【实验方案1】 双孔水平分布,其孔心连线方向与压缩方向垂直。
【实验方案2】 双孔垂直分布,其孔心连线方向与压缩方向平行。
【实验方案3】 三孔正置正三角形分布,其中有一相邻两孔的孔心连线与压缩方向垂直。
【实验方案4】 三孔斜置正三角形分布,其中有一相邻两孔的孔心连线与压缩方向平行。
【实验方案5】 四孔呈正方形排列,其底边两孔的孔心连线与压缩方向垂直。
【实验方案6】 四孔呈菱形排列,其相邻两孔心连线与压缩方向的夹角为45°。
对于同一组试样而言,其胞孔半径Ri均相同。因此,试样的孔隙度
(102)
式中,N为胞孔的个数。
由式(102)可以得到
(103)
已知圆柱体试样外径Ro=15 mm,孔隙度ψ=0.1,由式(103)可以计算出各组试样的胞孔半径Ri。对每组试样分别设计两种胞孔分布半径,数据见表9。

表9 胞孔结构参数
图43(a)为两种不同布孔方式和两种不同胞孔分布半径的双孔试样接触压缩过程中的P-S曲线;图43(b)为两种不同布孔方式和两种不同胞孔分布半径的三孔试样接触压缩过程中的P-S曲线;图43(c)为两种不同布孔方式和两种不同胞孔分布半径的四孔试样接触压缩过程中的P-S曲线(PII1、PII2、PIII1、PIII2、PIV1、PIV2为图42的布孔方式)。

图43 不同孔分布胞体的力-位移曲线
由图43(a)可知,当胞孔分布半径(即孔距)相同时,水平布孔方式比垂直布孔方式的失效力大。这表明,水平布孔的双孔试样的接触强度优于垂直布孔方式,其因素是水平布置时的两胞孔应力集中区与胞体接触应力区之间的距离比垂直布孔时的远,应力干涉作用较弱,因此,水平布孔的双孔试样具有更高的接触强度,这与类建筑材料的均布外载荷下的多孔材料的宏观力学形态[34]正好相反,可见接触应力在分析多孔结构强度时是不容忽视的。当布孔方式相同时,胞孔排列半径越大,则双孔试样的失效力越大,表明其接触强度越高,这是由于胞孔排列半径增大时,孔距随之增大,从而削弱了孔与孔之间的应力干涉作用,因此,接触强度随着孔距的增大而增大。
由图43(b)可知,胞孔分布半径较大的斜置正三角形分布方式的三孔试样具有最大的失效力,其接触强度最高。这是由于三孔呈斜置正三角形分布时,孔的应力集中区离接触应力区的距离较远,应力干涉作用较弱。随着胞孔分布半径的增大,孔距增大,3个胞孔应力集中区之间的相互干涉作用降低,从而使试样具有更高的接触强度。
由图43(c)可知,与菱形排列相比,胞孔呈正方形排列的试样明显具有更高的接触强度,且随着胞孔分布半径的增大,其接触强度变得更高。这是由于菱形排列时,上、下两胞孔离接触区较近,使胞孔应力集中区与接触应力区的干涉作用加强,从而降低了试样的接触强度。
对比双孔试样、三孔试样、四孔试样的P-S曲线,胞孔布阵形式对试样接触强度的影响远比胞孔分布半径对试样接触强度的影响程度大。因此,在设计具有相同孔隙度的多孔厚壁胞体的接触强度时,胞孔布阵分布形式是不可忽视的重要因素。
3.6 混合多孔结构对厚壁胞体接触稳定性影响试验研究
在工程中,HTSSLC基体的孔形状随机性较大,其接触强度将随不同结构孔在烧结体中的比例而变化。由于工程中烧结体中的孔结构形态及其比例是可以测量的,因此,混合孔结构对厚壁胞体接触稳定性影响规律将为HTSSLC的结构设计提供依据。
本研究团队设计了由4种典型形状胞孔组成的混合孔结构厚壁胞体模型(Model of Thick Wall Solo-Cell Structure with Compound Hole,MTWSCS-CH),并依据该模型,制备了混合孔结构胞体结构试样,采用YE-600型液压式压力试验机对试样进行接触压缩试验(contact compression experiment),探讨混合孔结构形态、孔隙度及布孔方位对厚壁胞体接触稳定性(contact stability of thick wall cellular structure)的影响,并结合有限元法讨论其失效机理。
3.6.1 混合孔结构厚壁胞体模型
假设厚壁胞体材料中含有KN种形状的胞孔,各种形状胞孔所占的孔隙度分别为ψi(i=1,2,…,KN),则该材料的总孔隙度
(104)
【定义2相对孔隙度ψi】 各形状胞孔的孔隙度占总孔隙度的百分比。
由相对孔隙度定义,可得
ψri=ψi/ψ
(105)
式中,ψri为i种形状胞孔所占的相对孔隙度。
为了简化,设轴向长度为Lt的圆柱体胞体中只含有正三角形胞孔(regular triangle hole)、正四边形胞孔(regular quadrangle hole)、正六边形胞孔(regular hexagon hole)和圆形胞孔(circular hole)等4种典型形状的胞孔(即KN=4),且每种形状的胞孔数量均为1,横截面见图44。

图44 异型孔厚壁胞体多孔结构
图44中,正三角形胞孔、正四边形胞孔、正六边形胞孔以及圆形胞孔的尺寸以其内切圆半径衡量,分别记为Ri 1,Ri 2,Ri 3,Ri 4,各孔中心均匀分布在半径为Rd的圆周上,胞体外径为Ro,4种形状胞孔所占的孔隙度分别记为ψ1,ψ2,ψ3,ψ4,胞体结构的总孔隙度为ψ,则各形状孔的孔隙度
(106a)
(106b)
(106c)

(106d)
由式(104)和式(106)可得该混合孔胞体的总孔隙度
(107)
通过比较式(107)中各项系数可知,上述4种形状孔洞的尺寸(内切圆半径)改变对胞体总孔隙度的影响各有差异,其中三角形孔洞的尺寸改变对胞体总孔隙度的影响最大,而圆形孔洞的尺寸改变对胞体总孔隙度的影响最小。
由式(105)和式(106)可得正三角形胞孔、正四边形胞孔、正六边形胞孔和圆形胞孔的相对孔隙度
(108a)
(108b)
(108c)
(108d)
各种形状胞孔的相对孔隙度之和满足
ψr1+ψr2+ψr3+ψr4=1
(109)
通过比较(108)各式中分子的系数可知,当各种形状胞孔的尺寸(内切圆半径)均相同时,正三角形胞孔的相对孔隙度最大,而圆形胞孔的相对孔隙度最小。
3.6.2 试验设计
根据建立的混合孔厚壁胞体多孔结构模型,按照图44设计试验试样。
【设计1孔隙度分配(porositydesign)】 对各种形状胞孔的孔隙度分配进行了C1~C5等5种情况设计,并由式(108)计算出孔形尺寸参数。其中,C1,C2,C3,C4为各孔形的孔隙度非均匀分配,分别代表正三角形胞孔、正四边形胞孔、正六边形胞孔和圆形胞孔的孔隙度占主导地位;C5为各孔形的孔隙度均匀分配见表10。

表10 H59铜圆柱体试样尺寸参数表
【设计2胞孔分布半径设计(DesignofCellularPores’DistributionDiameter,DCPDD)】 对C5种孔隙度分配情况,即孔隙度均匀分配情况设计了两种胞孔分布半径,分别为Rd=6 mm和Rd=7 mm。
【设计3布孔方位设计(DesignofCellularPores’DistributionPattern,DCDP)】 对C5种孔隙度分配情况,且Rd=7 mm的试样设计了两种布孔方向(见图44(a)和图44(b))。
图44(a)中的正三角形胞孔为斜向受力(inclined load),正四边形胞孔和正六边胞形孔为对边受力(opposite load);图44(b)中的正三角形胞孔为正向受力(vertical load),正四边形胞孔和正六边形胞孔为对角受力(diagonal load)。
采用液压力试验机对各试样进行径向(y向)压缩试验,并记录相应的P-S曲线,试样压缩试验示意图见图34。
3.6.3 混合孔结构对胞体接触强度的影响结果分析
(1)孔隙度分配对接触强度的影响图45为胞孔分布半径为7 mm的5种不同的孔隙度分配情况下的试样接触压缩的P-S曲线。

图45 不同孔隙度分配下混合型孔胞体试样的P -S曲线
由图45可知,C5种孔隙度分配情况,即孔隙度均匀分配情况时的失效力最大,为77.42 kN;C1,C2,C3,C4等4种孔隙度分配情况的失效力分别为57.32 kN,61.20 kN,66.18 kN和70.54 kN,与C5种孔隙度分配情况相比,分别降低了26%,21%,15%和9%。这说明在总孔隙度相同的情况下,正三角形胞孔、正四边形胞孔和正六边形胞孔所占的孔隙度比重增加均会导致材料接触强度的降低,其中正三角形胞孔的影响最大。为了提高厚壁胞体材料的接触强度,应该尽量降低正三角形胞孔、正四边形胞孔和正六边形胞孔孔隙度所占的比重,并尽可能使各种形状胞孔的孔隙度均匀分配。依据P-S曲线分区理论(见图36),由图45可知,虽然各胞孔的孔隙度分配情况不同,但是这5种情况的P-S曲线在初始预紧力区和基体弹性变形区表现出高度的一致性,而在胞孔结构变形区产生偏差,导致最终失效力的不同。
(2)胞孔中心分布半径对接触强度的影响图46为各胞孔孔隙度均匀分配时,胞孔分布半径分别为6 mm和7 mm的混合孔胞体试样接触压缩的P-S曲线。

图46 不同胞孔分布半径下混合孔胞体试样的P -S曲线
由图46可知,对于胞孔分布半径为6 mm的混合孔胞体试样,其失效力为73.30 kN,与胞孔分布半径为7 mm的混合孔胞体试样相比下降了5%。这是因为当胞孔分布半径降低时,孔与孔之间的距离变小,胞孔应力集中区之间的相互应力干涉作用加强,从而导致混合孔胞体结构接触强度的下降,这与图44中同形孔的结果相同,说明无论胞孔形状如何,若要提高多胞体结构材料的接触强度,应尽量增大胞孔之间的距离。
(3)布孔方位对接触强度的影响图47为各胞孔的相对孔隙度相同时的混合孔胞体试样接触压缩的P-S曲线(布孔方位形式见图44(a)和图44(b))。

图47 不同布孔方位的混合孔胞体试样的P -S曲线
由图47可知,按图44(b)布孔方位的试样,其失效力为60.76 kN,与按图44(a)布孔方位的试样相比下降了22%。这说明胞孔的排布方式对多胞体结构材料的接触强度影响较大,对角受力的四边形胞孔及六边形胞孔的存在将极大地削弱材料的接触强度。
(4)混合孔与同形孔胞体接触强度的对比将胞孔孔隙度均匀分配且胞孔分布半径均为7 mm的混合孔与同形孔(均为圆形孔)试样接触压缩时的P-S曲线进行对比(见图48)。同形孔试样的失效力为81.34 kN,与之相比,混合孔试样的失效力降低了5%,这说明混合孔的存在将导致多胞体结构材料接触强度的降低。因此,为了提高厚壁胞体材料的接触强度,应该尽可能地制备圆形胞孔结构形态。

图48 孔隙度均匀分配下同形孔与异形孔胞体试样的P -S曲线
3.6.4 模型试验验证与分析
为了讨论混合孔胞体接触失稳的破坏形态及裂纹萌生机理,开展了试验与仿真分析研究(见图49)。

图49 孔隙度均匀分配的混合孔胞体试样破坏形貌分析
由图49(a)可知,正三角形胞孔的裂纹最先产生在右上部的孔边处,而不是产生在其上部尖角处,这与均布外载荷作用下的裂纹萌生位置[36]有很大差别;在三角形孔口的下部尖角处产生次生裂纹,裂纹的扩展方向如箭头所示指向初始接触点,而不是平行于外载荷的加载方向。这说明了非均匀分布的接触力对胞体结构的破坏形式影响很大。
由图49(b)可知,若分别以上、下初始接触点为圆心作接触应力圆,与正三角形胞孔外切,切点分别为A和B,比较两个外切圆的半径可知,在点A处先产生初始裂纹,接着在点B处产生次生裂纹。该分析结果与试验结果完全符合(混合孔多胞体结构的裂纹源发生及扩展位置分析方法见文献[37])。
图49(c)为有限元法得到的最大主应力分布云图,图中注释小圆圈为正三角形胞孔孔口的拉应力集中点,箭头表示孔口周围拉应力梯度变化最快的方向,由有限元结果和试验结果对比可知,对混合孔多胞体结构而言,其裂纹同样萌生于微孔孔口边缘拉应力集中点处,且裂纹同样沿着孔口周围拉应力梯度变化最快的方向扩展。
3.7 环境工况对厚壁胞体接触稳定性影响的试验研究
3.7.1 温度对厚壁胞体接触强度的影响
为了讨论HTSSLC胞体对接触工况适应性,本研究团队探讨了其温度和切向力对其接触强度的影响。考虑试验材料的弹塑性性能,在常温(20 ℃)和高温(300 ℃)等两种工况下,采用YE-600液压式压力试验机对试样进行接触压缩试验,探讨了温度对厚壁胞体材料接触强度及稳定性的影响。此外,利用ANSYS有限元分析软件建立了其单孔结构胞体及多孔结构胞体摩擦接触力学的有限元模型,探讨环境温度及切向摩擦力对胞体接触表面及内部应力分布的影响。
本研究采用的试样几何形状见图42,几何参数见表11。

表11 H59铜圆柱体试样几何参数
接触强度试验原理见图50。试验时,温度由传感器控制,刚性压头对试样施加外载荷P,载荷速率为112 N/s,刚性压头的位移S由位移传感器记录。

图50 高温试验示意
图51为含有圆形单孔胞体、双孔胞体、三孔胞体以及四孔胞体等试样在20 ℃与300 ℃时的P-S曲线。由图51可知,单孔胞体、双孔胞体、三孔胞体和四孔胞体等试样在300 ℃时的失效力(42.14 kN,68.50 kN,62.58 kN和71.00 kN),与20 ℃时的失效力(49.49 kN,78.99 kN,70.27 kN和81.34 kN)相比,分别减小了14.85%,12.71%,10.94%和13.29%。单孔胞体、双孔胞体、三孔胞体和四孔胞体等试样在300 ℃时的失效位移(2.10 mm,4.75 mm,5.00 mm和3.95 mm),与20 ℃时的失效位移(分别为1.04 mm,2.40 mm,2.40 mm和2.00 mm)相比,分别增大了101.92%,97.92%,108.33%和97.50%。

图51 试样在20 ℃与300 ℃的P -S曲线
这说明温度对厚壁胞体多孔材料的承载能力及变形程度有很大的影响,无论胞孔结构如何,温度升高都将导致材料接触承载能力的降低,变形程度的增大。对不同的胞孔结构而言,由温度升高引起的接触强度的下降和接触变形增大的程度差别不大,这反映出温度影响主要是通过改变材料的力学性能,而与胞孔结构参数关联很小。因而,对于厚壁胞体而言,当将其应用于高温接触部件时,材料的高温力学性能(如弹性模量、屈服强度以及抗拉强度等)应优于孔结构特征设计。
图52为在20 ℃和300 ℃等两种工况条件下,单孔胞体、双孔胞体、三孔胞体和四孔胞体等试样接触压缩时的P-S曲线。由图52可知,在20 ℃和300 ℃等两种温度条件下,单孔胞体试样的失效力都是最小的,而四孔胞体试样的失效力是最大的。这说明无论环境温度如何,四孔胞体试样的接触强度都是最大的,双孔胞体试样和三孔胞体试样居中,而单孔胞体试样的接触强度是最小的。20 ℃时,四孔胞体试样的失效力和失效位移分别比单孔胞体试样高64.36%和130.77%。300 ℃时,四孔胞体试样的失效力和失效位移分别比单孔胞体试样高68.49%和126.19%。温度一定的条件下,上述4种胞孔结构的试样在初始预紧力区和基体弹性变形区的P-S曲线几乎重合,而在胞孔结构变形区产生分歧,这是由于在预紧力区和基体弹性变形区时,局部接触应力只引起基体变形而没有对胞孔结构产生影响,而在胞孔结构变形区时,逐渐增大的接触应力将扩展至胞孔边缘,引起胞孔结构的变形,由于试样的胞孔结构不同,因此产生的变形量不同,从而导致该变形区的曲线产生分歧。
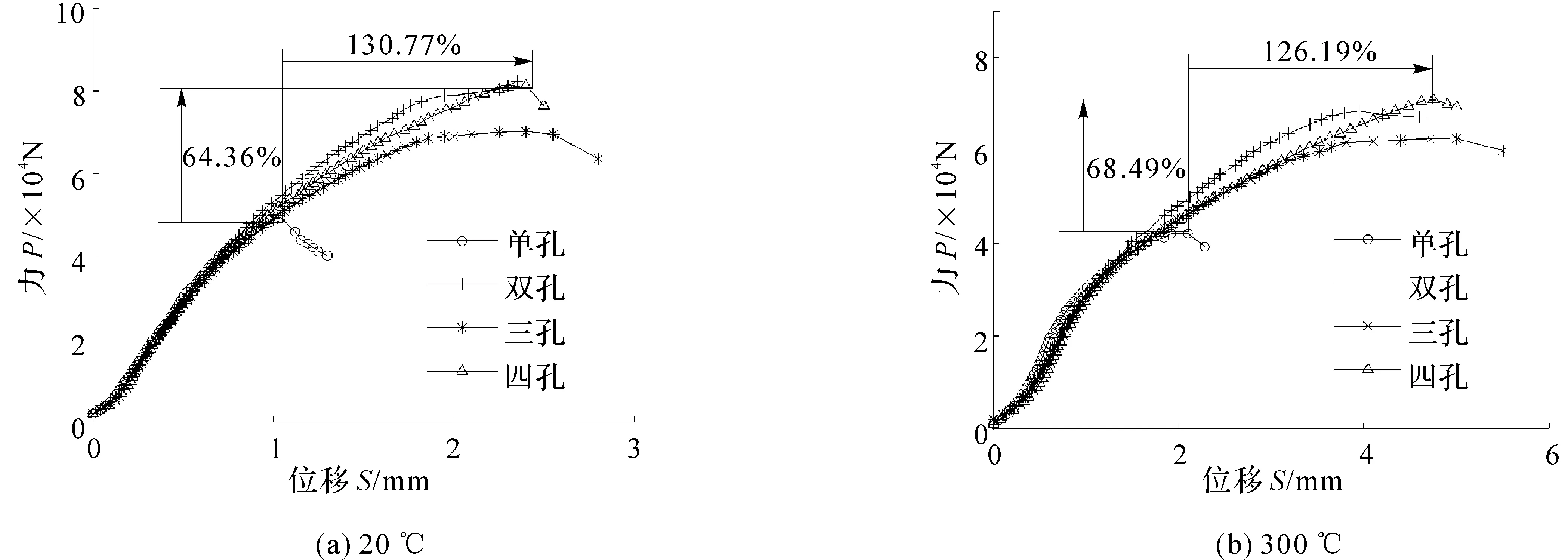
图52 试样接触压缩时的P -S曲线
应当指出的是,在本研究团队的研究工作中,不同胞孔结构试样的总孔隙度是相等的,由此反映出,在相同的孔隙度下,具有小而分散孔结构形态的材料,其接触强度远高于大而集中的孔结构形态材料。
图53为单孔胞体试样和三孔胞体试样在20 ℃和300 ℃时的破坏形貌图。由图53可知,接触过载时,胞体试样均产生裂纹破坏。此时,单孔胞体试样在20 ℃和300 ℃时的接触半宽分别为4.71 mm和8.04 mm,承载方向的直径分别变为29.02和28.01 mm。而三孔胞体试样在20 ℃和300 ℃时的接触半宽分别为5.42 mm和11.44 mm,承载方向的直径分别变为28.03 mm和26.04 mm。

图53 试样破坏形貌
所有试样的裂纹均萌生于胞孔边缘且离初始接触点最近的地方,并朝着初始接触点方向扩展,这说明温度虽然对多孔试样的承载能力和变形影响很大,但是裂纹萌生位置及扩展方向均与环境温度无关。这是由于温度的升高仅仅引起材料基体力学性能的改变,例如H59铜的弹性模量和屈服强度均随着温度的升高而降低,从而导致材料整体承载能力下降和变形程度增大,但是温度升高并没有改变胞孔结构对于载荷的响应行为,因此并不影响材料的破坏形式(即裂纹的萌生与扩展)。然而,值得注意的是,温度升高引起了裂纹深化,这是由于试样高温变形程度较大所引发的。
3.7.2 切向力对厚壁单胞结构体接触强度的影响
作为摩擦学材料,摩擦过程中的切向力不仅影响了其承载能力,而且也影响其耐磨性。特别是,为了提高厚壁胞体材料在高副接触条件下的工作可靠性,应研究切向力对其接触强度的影响。本研究团队采用切向力与法向力耦合作用时的接触力学模型(见图54)进行分析。

体Ⅰ为单孔厚壁胞体(Ro为单孔厚壁胞体外径,Ri为单孔厚壁胞体内径);体Ⅱ表示刚性平面;θ为胞体孔壁上任一点与靠近接触区一侧的胞孔竖直对称轴所成的角度。【θ正负号规定】 位于胞孔垂直对称轴右侧的角度为正,位于其左侧的角度为负。
【假设8】 单孔厚壁胞体(体Ⅰ)与刚性平面(体Ⅱ)在接触点处仅产生相对运动的趋势,而没有产生相对滑动和滚动,刚性平面(体Ⅱ)对单孔厚壁胞体(体Ⅰ)施加垂直挤压力P和水平牵引力Q。
采用有限元模型(见图55)分析其接触力学特性。

图55 切向力与法向力耦合作用时单孔厚壁胞体接触有限元分析模型
在切向力与法向力耦合作用时的接触力学模型(见图55)中,坐标原点位于厚壁胞体和刚性平面的初始接触点处,在预计接触区和微孔应力集中区进行网格细化,其计算参数及边界条件如下。
【模型结构参数】Ro=15 mm,Ri=4.743 4 mm。
【模型材料参数】 胞体材料为H59铜材料,其弹性模量E=98 000 MPa,泊松比μ=0.3,摩擦因数f=0.45[33]。
【模型单元类型】 单孔厚壁胞体采用PLANE42平面应变单元,接触面采用二维面-面接触单元;刚性平面为目标面,采用目标单元TARGET169;单孔厚壁胞体为接触面,采用接触单元CONTAC171。
【模型边界条件】 将单孔厚壁胞体中y=Ro的所有节点的y向位移进行耦合(符号记为CP),使其不发生转动;对其上部微小区域外表面节点进行全约束,P=3 000 N,Q分别取为0 N,500 N和1 000 N。
3.7.3 模型的可信度评估
对比无摩擦作用时(即Q=0且f=0)最大接触压力q0的有限元数值解与相应的解析解[38](见表12)。由表12可知,采用本模型得出的数值解具有足够精度(误差小于1%),可用于分析厚壁胞体与刚性平面摩擦接触时的切向力影响。

表12 无摩擦情况解析解与数值解的结果对比
3.7.4 切向力对胞体接触表面应力的影响
图56为3组不同的切向力对厚壁胞体结构接触表面应力的影响规律:

[注]:q0为Q=0 N时的最大接触压力;a为Q=0 N时的接触半宽;σx/q0为接触表面x向的当量应力;σy/q0为y向当量应力;σxy/q0为合成当量剪应力。
(1) 由图56(a)可知,当没有切向力作用时,x向当量应力(σx/q0)均为压应力,其在导向边((x/a)>0)和拖动边((x/a)<0)各有一个峰值出现,且关于y轴对称分布;当存在切向力作用时,接触表面导向边的压应力峰值随着切向力的增大而增大,而拖动边的压应力峰值逐渐减小,并最终出现拉应力,且最大拉应力位于(x/a)=1处(即拖动边的边缘)。
(2) 由图56(b)可知,当没有切向力作用时,y向当量应力(σy/q0)均为压应力,其峰值位于接触中心处((x/a)=0),且关于y轴对称分布;当存在切向力作用时,压应力的峰值略有降低,且略微向拖动边偏移,偏移量随着切向力的增大而有所增大。就整体而言,切向力对接触表面y向当量应力(σy/q0)的影响不是非常显著。
(3) 图56(c)可知,当没有切向力作用时,当量剪应力(σxy/q0)关于接触中心对称分布,其拉应力峰值出现在拖动边,而压应力峰值出现在导向边;当存在切向力作用时,其压应力峰值随着切向力的增大而增大,且位置逐渐向拖动边((x/a)<0)偏移,而拉应力的峰值随着切向力的增大而减小,且峰值位置逐渐向拖动边的边缘((x/a)=-1)偏移。
3.7.5 切向力对接触压力及摩擦力的影响
切向力不仅影响接触表面的应力分布,而且对接触压力q及摩擦应力σf的分布也有一定的影响(见图57):

图57 单孔厚壁胞体接触压力及摩擦应力分布
(1) 由图57(a)可知,当没有切向力作用时,接触压力峰值位于接触中心,且关于y轴对称分布;当存在切向力作用时,接触压力的峰值随着切向力的增大而略微下降,且略微向拖动边((x/a)<0)偏移。然而总体来说,r1切向力对法向接触压力和接触面积的影响不大。
(2) 由图57(b)可知,当没有切向力作用时,摩擦应力关于接触中心对称分布,其拉应力峰值出现在导向边,而压应力峰值出现在拖动边;当存在切向力作用时,其拉应力峰值随着切向力的增大而增大,且拉应力峰值位置向拖动边((x/a)<0)偏移,而压应力的峰值随着切向力的增大而减小,且压应力峰值位置向拖动边的边缘((x/a)=-1)偏移。
为了进一步讨论在切向力条件下,孔结构形态及其孔隙度对接触压力及摩擦力的影响,在相同外载荷工况下,分析了多孔厚壁胞体与单孔厚壁胞体当量接触压力(q/q0)及当量摩擦应力(σf/q0)的分布情况(见图58)。

图58 单孔与多孔厚壁胞体接触压力及摩擦应力对比
由图58可知,无论切向力大小如何,双孔厚壁胞体、三孔厚壁胞体或四孔厚壁胞体的接触压力及摩擦应力的分布及变化规律均与单孔厚壁胞体相同,这说明多孔厚壁胞体的接触压力及摩擦应力随切向力的变化情况与单孔厚壁胞体相同。此外,多孔厚壁胞体的接触压力的大小几乎与单孔厚壁胞体相同;而多孔厚壁胞体的摩擦应力在峰值处与单孔厚壁胞体的有一定的差别,但是随着切向力的增大,这种差别逐渐变小乃至消失。
【推论18】 对厚壁胞体而言,在总孔隙度相同的情况下,无论是单孔结构还是多孔结构,即微孔结构的改变对胞体接触压力及摩擦应力的影响很小。
4 多元固体润滑体的组分设计及其真空熔渗工艺研究
在高温摩擦过程中,高温发汗自润滑材料(HTSSLC)中的润滑体组分析出于摩擦表面并形成润滑膜,从而实现高温自润滑功能。摩擦表面润滑膜减摩性能及其覆盖率取决于HTSSLC熔渗制备过程中形成的微观结构特征及其润滑体组分性能。因此,多元固体润滑体的组分设计及其真空熔渗工艺研究是高温自润滑技术的关键研究内容。
本研究团队依据多元润滑体的功能要求及熔渗工艺特点,应用相图理论对复合润滑体组分进行设计和优化;并对HTSSLC的真空熔渗制备工艺展开研究。
4.1 多元固体润滑体设计
基于HTSSLC润滑体的润滑功能及制备工艺特点,多元固体润滑体(Compound Solid Lubricant,CSL)组分设计应满足如下准则(见表13)。

表13 多元润滑体性能要求
为满足上述设计准则,本研究团队拟采用软金属(soft metal)作为固体润滑体的主要组分。为使软金属能有效地熔渗于金属陶瓷基体微孔,软金属的物理性能显得非常重要,特别是在不同温度下与金属陶瓷烧结体的接触润湿性能直接影响到软金属的熔渗效果。表14为多元固体润滑体组分设计研究中拟采用的软金属的化学成分及其物理性能。

表14 Pb,Sn和Ag元素的物理性能及接触润湿角特性[39]
[注] 接触润湿角是为了研究软金属与金属陶瓷基体的润湿性,采用简化座滴法测量。其测量过程如下:在不添加造孔剂情况下,按汗腺式微孔基体烧结工艺制备出密实圆盘试片,试片经1.0 μm金刚石研磨膏抛光,在丙酮溶液中经超声波清洗后水平放置于真空室;纯净的Pb,Sn或Ag等试块(100 mg)经酸洗除去表面氧化膜后,在丙酮溶液中经超声波清洗后置于试片之上。真空室抽真空至2×10-4Pa,快速加热至设定温度,保温45 min后随炉冷却至室温。
由表14可知,仅靠单元素组分难以实现上述设计准则(见表13),故而,需通过多组分复配设计实现。
用金相法测量金属液滴在金属陶瓷衬底的润湿角。结果表明,温度在800 ℃以下时,Pb和Sn与金属陶瓷试片的润湿角均大于70°,可见其单质组分与金属陶瓷的润湿性较差。因此,通过多种软金属元素复配和优化,获得与金属陶瓷基体具有良好润湿性和润滑性能的复合润滑体是HTSSLC设计的重要内容。
4.2 复合润滑体合金的热膨胀系数及熔点设计
基于高温发汗自润滑工作原理,采用热膨胀系数较大的复合润滑体有利于润滑元素在摩擦热-应力良好作用的情况下析出至摩擦表面。由表14可知,Pb,Sn和Ag等的膨胀系数都较大,因此,当复合润滑体以Pb,Sn和Ag为主要组分进行组分设计时,其润滑体都具有比金属陶瓷基更高的热膨胀系数,可满足复合润滑体从汗腺微孔中析出至摩擦表面。
为了保证所制备的复合润滑体的热膨胀系数大于金属陶瓷基体的热膨胀系数,本研究团队采用DIL-402C热膨胀仪(Netzsch,德国)对组分为复合润滑体47Pb28Sn19Ag6Cu的热膨胀系数进行了测量。测量结果表明,复合润滑体47Pb28Sn19Ag6Cu的平均热膨胀系数为2.561 3×10-5,远大于金属陶瓷基体基体材料的平均热膨胀系数(1.003 1×10-5),故此,Pb-Ag-Sn三元复合润滑体有利于高温摩擦过程中润滑剂的析出。
一般认为,复合润滑体的熔点设计可基于软金属合金相图。图59为Pb-Ag-Sn三元合金相图,它反映了不同合金元素配比时的熔点。

图59 Pb-Ag-Sn三元系合金液相面投影图
复合润滑体合金的热膨胀系数及熔点设计,首先应参照图59设计出满足500 ℃温度范围的复合润滑体组分(见表15);再通过摩擦试验和湿润性研究,优化组分配比。

表15 复合润滑体组分配比
4.2.1 润湿性设计
润湿现象是指固体表面上气体被液体逐步取代的过程。当金属液滴和母材基板相互接触时,性质不同的金属液滴会在母材基板表面上形成一定形状的扁平液滴(见图60)。
当金属液滴和母材基板之间不存在物理互溶、渗透和任何化学反应,即仅以色散力(chromatic dispersion energy)相互作用时,存在如下关系
γsg=γsl+γlgcosθ
(110)
式中,γsg为气固表面张力;γsl为液固界面张力;γlg为气液表面张力;θ为金属液滴对母材的润湿角。
或

(111)
式(110)或式(111)反映出金属液滴对母材的润湿角与母材气固表面张力、气液表面张力及液固界面张力之间的关系符合杨氏方程(Young Equation)[40]。
润湿角θ表示金属液滴对母材基板的润湿程度,θ=0°表示完全润湿;θ=180°表示完全不润湿。由此,当γsg和γlg为某一定值时,γsl与θ有某种正比的关系——γsl愈小,θ也愈小——金属液滴与母材间的表面张力愈小,越容易润湿,故要促进金属液滴与母材之间的润湿,则需要使γsg增加,或使γlg和γsl下降。
实现式(110)或式(111)最常采用的技术手段是将第二相中介物质(如钎剂)覆盖在金属液与母材基板的表面间,使界面情况发生变化。此时存在
γsf-γsl=γlfcosθ
(112)
式中,γlf为金属液与第二相中介物质界面张力。
如果使用二相中介物质后可以使γsf>γsg或使γlf>γlg,则可大幅度地改善熔融体与母材之间的润湿性能。
研究表明[41],如果熔态合金与母材之间存在一定的反应性时,通常能够很好地润湿,反之则较难润湿。因此,要提高熔态复合润滑体合金对于基体的润湿性,就需要提高润滑体合金成分与基体主要成分的可反应性。
本研究中制备的HTSSLC基体为高速钢基陶瓷,其主要成分为M3高速钢,主要组元为Fe,因而,复合润滑体合金应与Fe元素具有良好的反应性。
由图61[41]可以看出,Pb和Ag等两种元素与Fe元素的互溶度很小,而且没有金属间化合物产生,这导致Pb或Ag对基体的润湿性很差,故需要通过在Pb-Ag合金中加入与Fe有较好反应性的第三种合金元素以提高润滑体合金对基体材料的润湿性。
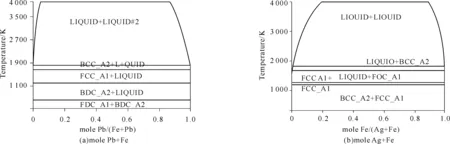
图61 Pb-Fe与Ag-Fe二元合金相图[41]
图62为Sn与Fe的合金相图[41]。由图62可知,在Sn-Fe合金中,Sn与Fe有金属间化合物产生,具有较好的反应性及润湿性,因而向Pb-Ag合金中加入Sn可以提高合金对基体材料的润湿性。Sn是较好的软金属润滑剂,具有较好的润滑性能。加入Sn还可以降低Pb-Ag合金的熔点,降低液态合金的表面张力,有利于复合熔渗过程;然而,Sn在高温下易氧化而生成SnO2,最终失去Sn的润滑性,故应控制其在复合润滑体中的比例。
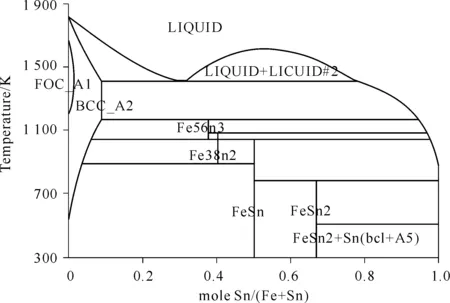
图62 Sn-Fe二元合金相图[41]
此外。Cu在高温下与Fe具有较大的互溶度。在1 200 ℃时,Cu能溶入近5%的Fe。因此,加入Cu也可以改善润滑体合金与基体材料的润湿性,但加入Cu会使润滑体合金熔点升高,不利于熔渗的进行,因而应控制其含量。基于以上分析,复合润滑体合金应以Pb和Ag为主要成分,加入一定量的Sn和Cu,提高润湿性。
图63为在试验温度为550 ℃时,采用钎剂102作为熔渗剂,不同组成比例的Pb-Ag合金在M3高速钢母材表面润湿角的变化情况。

[测量条件] 测试在真空感应加热炉中进行,母材为M3高速钢制φ58×8圆盘,表面磨削加工;测试温度550 ℃,保温时间2 min。
从图63可以看出,Pb对于M3高速钢母材的润湿性很差,在使用钎剂102的情况下,润湿角仍达到88°。在合金中加入少量Ag后,润湿性有所改善。随着Ag含量进一步增加,熔态合金与M3高速钢母材表面润湿角逐渐变大、铺展面积变小,润湿性变差。这是由于随着Ag含量的增加,合金熔点提高,在试验温度不变时,熔态合金粘度变大,与M3高速钢母材润湿性变差,润湿角逐渐增大。
图64为550 ℃时Pb与Ag比例为7∶3,在Pb-Ag-Sn合金中加入Sn时与M3高速钢基板润湿角的关系曲线。

图64 Pb-Ag-Sn合金Sn含量对润湿性影响
从图64可见,随着Sn含量的增加,Pb-Ag-Sn润湿角变小,润湿性提高。究其原因,虽然熔态Pb和Ag与母材在液态或固态下的润湿性差,但加入Sn后,由于Sn与Fe能在高温下反应生成金属间化合物,提高了其与母材的反应性,使Pb-Ag-Sn合金的润湿性得到改善。图64表明,Sn含量越高,润湿性越好。
图65为550 ℃条件下,当Pb,Sn和Ag比例为5∶3∶2时,在Pb-Ag-Sn-Cu合金中添加不同含量的Cu,对于M3高速钢基板润湿性影响的关系曲线。

图65 Pb-Ag-Sn-Cu合金Cu含量对润湿性影响
由图65可见,与Pb-Ag-Sn合金相比,加入Cu将使其润湿性改善更加明显,铺展面积显著增大(由于此时的润湿角很小,不便测量,只能对铺展面积进行测量)。显然,Cu在高温下与Fe的高互溶度,改善了润滑体的润湿性,但Cu含量过大时将造成合金熔点上升,影响润滑体在较低工作温度下的润湿性。
4.2.2 润滑性设计
软金属固体润滑剂剪切强度低。在发生摩擦时,软金属会在对偶材料表面形成转移膜,使摩擦发生在转移膜与软金属本身之间,从而降低摩擦因数,减少磨损,其中以Pb和Ag为其代表。
Pb是优良的固体润滑剂,但在高温工作时暴露于空气之中,将发生氧化,生成PbO。PbO是润滑性能很好的高温润滑剂,400 ℃以上时,其润滑性能比MoS2更好。370~480 ℃时,PbO氧化为Pb3O4,摩擦因数变大;超过480 ℃后,Pb3O4分解重又生成为PbO,且在480~850 ℃的连续范围内显示出很好高温润滑性能。
在高温摩擦过程中,WC-Ni-Mo-PbO中的Pb和PbO能与基体材料或对偶材料中的W反应生成具有良好高温润滑性能的PbWO4[42]。
Ag的熔点较高,在大气中的化学性质十分稳定,故而适用于大气高温环境下的润滑。同时,由于Ag具有良好的导热性能,在导热性差的陶瓷表面成膜时,可有效改善陶瓷的摩擦磨损性能[43-44]。在高温时,Ag和AgO与W和V反应,可进一步降低摩擦因数。作为软金属润滑剂,在较低温度条件下(<500 ℃),Pb和Ag能保证复合材料的自润滑性能;在高温条件下,Pb和Ag的氧化生成物将起主要润滑作用。可见,当Pb和Ag作为复合润滑体的主要成分时,将会获得较好的高温润滑性能。
图66展示出当润滑体合金中Sn和Ag的组分比例不变时,Pb含量在40wt%~85wt%变化时对摩擦因数的影响。

图66 Pb含量对复合润滑体润滑性的影响
由图66可见,当Pb含量为40wt%时,其摩擦摩擦因数较低;此后,摩擦因数随Pb含量的增加而增加。究其原因,当Pb含量较高时,合金中Sn的比例下降,合金对基体及对偶件的润湿性与粘合度降低,使摩擦表面形成的润滑膜易于脱落,造成基体与对偶件的表面接触,从而增大了摩擦因数。
图67为Pb含量为40wt%和85wt%时,摩擦后摩擦表面磨痕照片及相应的摩擦因数变化曲线。可以看出,当Pb含量为40wt%时(见图67(a)),对偶盘摩擦表面比较平整,而当Pb含量为85wt%时(见图67(b)),对偶盘摩擦表面有明显的粘着磨痕。

图67 Pb含量为40wt%及85wt%时对偶盘表面磨痕及摩擦因数
但当合金中的Pb含量为40wt%时,合金中Sn元素含量偏高,Sn在摩擦过程中会发生氧化,生成不具有润滑性能的SnO2,使润滑膜润滑性能变差,导致摩擦因数随着磨损时间增加而升高(见图67(c)),从而影响了摩擦过程的温度性。由此可见,润滑体的润滑性组分设计是非常复杂的过程,需要全面考虑影响因素。
4.3 多元固体润滑体真空熔渗工艺
多元固体润滑体对GLPS金属陶瓷的熔渗过程既是孔隙度被填充的过程,也是元素在烧结体中扩散的过程;其熔渗品质取决于压力、温度和时间等工艺参数。
图68报告了HTSSLC制备工艺原理流程,其中,虚线框内的工艺流程为汗腺式微孔烧结体制备过程。真空熔渗工艺(Vacuum Infiltrating Process,VIP)是指多元固体润滑体的二次复合过程。在VIP过程中,为了提高微孔填充率,采用了真空加压熔渗法(Vacuum Pressure Infiltration,VPI)。

图68 HTSSLC复合工艺流程
4.3.1 工艺参数对熔渗质量影响研究
4.3.1.1 熔渗试验设备
基于HTSSLC熔渗工艺对熔渗设备的要求,本研究团队成功研发了一套感应熔渗试验装置(Induction Heating Infiltration Equipment,IHIE)(见图69),可在不同气氛环境下,完成无压熔渗、加压熔渗,或者无压-加压复合熔渗等工艺过程,实现高温发汗自润滑层制备。

图69 感应熔渗试验装置
感应熔渗试验装置(IFIE)由以下5个部分构成。
【part1全固态感应加热设备】 将电磁能量转换为热能,加热基体材料与润滑体合金。
【part2熔渗发生炉】 在熔渗过程中,为构建工艺气氛环境提供密闭空间。
【part3温度、气氛输送控制线路】 在熔渗过程中,控制熔渗温度和环境气氛。
【part4真空泵】 在熔渗过程中,建立真空环境。
【part5惰性或还原性气体发生系统】 在熔渗过程中,提供惰性气氛保护环境或还原气氛环境。
4.3.1.2 熔渗工艺过程
在润滑层熔渗制备时,如果熔态润滑体合金对基体材料的润湿角小于90°,熔态合金可在毛细作用下自发渗入材料内部。为了增加润滑层深度,减小润滑层的残余孔隙度,本研究团队采用真空加压熔渗法(VPI),其熔渗制备步骤见图70。
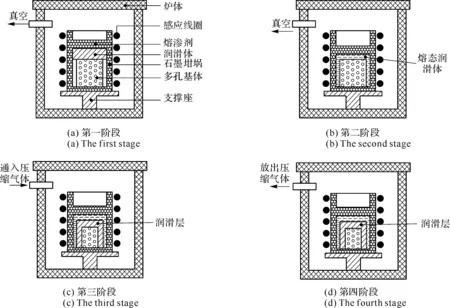
图70 HTSSLC真空熔渗工艺过程操作示意
【step1】 将多孔金属陶瓷基体、块状润滑体合金及熔渗剂依次装入熔渗炉内石墨坩埚中,打开真空泵(见图70(a));
【step2】 在真空条件下快速加热到熔渗温度,待润滑体合金熔液完全淹没多孔金属陶瓷基体,保温一段时间使基体微孔中的残存气体充分排出(见图70(b));
【step3】 通入高压氮气,保温保压一定时间,熔态润滑体合金在毛细作用及外加压力下进入基体微孔中形成润滑层(见图70(c));
【step4】 关闭加热开关,关闭高压气体进气阀,打开排气阀,待温度冷却至润滑体合金熔点以上100 ℃左右时打开炉子,从坩埚中取出试样(见图70(d))。
4.3.2 润滑层微观结构及润滑体元素分布
采用上述熔渗工艺制备的HTSSLC,其润滑体组分为47Pb28Sn19Ag6Cu。试验中各工艺参数如下:加热电流200~250 A,熔渗温度为700~800 ℃,真空下保持时间10~15 min,通入压缩气体压力为0.3~0.5 MPa,保压20~25 min。图71为HTSSLC熔渗前后试样照片。

图71 基体材料试样及熔渗后HTSSLC试样
从图71可以看出,熔渗前,基体试样存在微孔,表面粗糙(见图71(a));熔渗后试样表面由光亮的软金属复合润滑体包覆,润滑体与基体结合紧密(见图71(b))。说明该复合润滑体与基体材料具有良好的润湿性。
图72反映出不同元素在熔渗过程中达到的深度差别(例如,Pb熔深比Sn高)。图72(a)为图72试样剖开后,剖面上润滑层熔渗前沿部分微观结构照片,图中白色区域代表润滑体相,灰色区域为基体材料相。可见熔渗过程中,熔态润滑体在毛细力及外加压力的作用下进入到基体内部微孔中形成了高温发汗润滑层。从图72还可以看出,润滑层内只有部分孔隙被润滑体填充,还存在一些残余孔隙。图72(b)和图72(c)分别为Pb和Sn元素在相应区域的分布(同理可得到Ag,Cu元素的分布)。
显然地,这种差别除取决于被熔渗元素自身的物化性能外,也与被熔渗元素与金属陶瓷基体的润湿性有关。

图72 熔渗后润滑层微观结构及润滑剂元素分布
基于熔渗过程动力学(Dynamics Analysis of Infiltration Process)[45],可以推导出润滑层深度Lh与其润湿角之间的关系。
可以看出,润滑层的生成过程是熔态复合润滑体合金逐渐浸润多孔基体的动力学过程,其熔渗深度Lh与湿润角成正比。这表明,熔态复合润滑体与基体材料的润湿性越好,润湿角越小,同样条件下形成的润滑层深度越深。
4.3.3 熔渗率、残余孔隙度和相对密度表征
为了描述熔渗工艺对熔渗质量的影响,本研究团队就熔渗率、残余孔隙度和相对密度的表征方式进行定义。
【定义3熔渗率(InfiltrationPercentage)】 指熔渗到汗腺式微孔烧结体中的固体润滑剂质量占总质量的百分比。
【定义4残余孔隙度(ResidualPorosity)】 指熔渗后材料中残余孔隙的体积与材料总体积的比值。
【定义5相对密度(RelativeDensity)】 指熔渗后材料的实际密度与理论密度(汗腺微孔被固体润滑剂完全填充的密度)的比值。
熔渗率的高低是反映熔渗过程填充效果的指标之一。相对密度和残余孔隙度是反映材料制备工艺重要指标。熔渗率、残余孔隙度和相对密度采用液体静力平衡法测量[20],方法如下。
烧结体密度(Density of Sinter)
(113)
式中,ρdry为烧结体密度;mA为未熔渗固体润滑剂试样在空气中的质量,g;mB为熔渗固体润滑剂试样在空气中的质量,g;mC为熔渗固体润滑剂试样悬挂于水中的质量,g;mE为悬挂的丝与筐在水中的质量(皮重),g;ρW为在试验温度下蒸馏水的密度,g·cm-3。
复合材料密度(Density of Composite)
(114)
式中,ρwet为复合材料密度。
熔渗率(Infiltration Percentage)
(115)
相对密度(Relative Density)
(116)
式中,ψ0为汗腺式微孔烧结体的开口孔隙度,%;ρG为熔渗固体润滑剂的密度,g·cm-3;
残余孔隙度(Residual Porosity)
(117)
式中,mF为蒸馏水中煮沸2 h后熔渗固体润滑剂试样在空气中的质量,g。
4.3.4 熔渗压力对填充率的影响
在真空中向GLPS中熔渗固体润滑体时,可忽略孔隙中的气体受压缩而引起的反压力,因此,表面张力成为影响熔融固体润滑剂填充的主要因素。对于给定的熔融固体润滑剂和微孔烧结体而言,其表面张力γ和润湿角θ均为定值,此时,熔渗过程取决于烧结体中微孔的作用阻力,这一作用阻力可基于毛细管,由Young-Laplace方程确定[46]。
(118)
式中,FC为烧结体中微孔的作用阻力;γlg为液气界面张力,N·m-1;θ为熔融固体润滑剂与金属陶瓷间的润湿角,(°);r为等效孔隙半径,mm。
当θ<90°时,毛细管力为动力,FC>0,液相趋向于覆盖固相;当θ>90°时,FC<0,毛细管力为阻力,不利于熔渗。
显然,熔融固体润滑剂在真空条件下能否熔渗到微孔金属陶瓷烧结体孔隙之中,主要取决于所施加的熔渗压力是否大于熔渗过程中的毛细管阻力。
假设熔融固体润滑剂对微孔金属陶瓷烧结体的润湿过程是可逆的,润湿过程中无摩擦力存在,并忽略重力的影响,则熔渗过程完全取决于毛细管力大小,且毛细管力越大,则临界熔渗压力Flimit越大。因此,在工艺设计中,可基于熔渗压力预测熔渗过程能否顺利地进行。在不同熔渗温度下,γlg可根据Van Der Waals经验公式(Empirical formula)[47]计算。
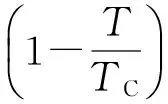
(119)
式中,γlg0为经验常数,N·m-1;T为熔渗温度,K;TC为熔融固体润滑剂临界温度,K;no为经验常数,常取no=1.2。
因此,只要知道被熔融固体润滑剂的临界温度,即可计算出γlg0,进而计算出微孔的作用阻力FC。只要熔渗压力大于FC,则熔渗可顺利地进行。
例如,Ag在1 273 K时,查得γlg=920 N·m-1[47],测得Ag与GLPS烧结体的润湿角为98°;当被熔渗的GLPS烧结体孔径为10 μm时,熔渗Ag时所需施加的理论压力应为0.3 MPa。而事实上,由于压力是等方向传递的,熔渗到烧结体孔隙中的熔融固体润滑剂的前沿方向随孔隙通道方向的变化而变换,因此,局部微观流动方向与宏观渗流方向并非始终一致,这对于具有内贯通微孔的烧结体而言,熔融固体润滑剂向微孔的浸渍将变得困难,使得烧结体孔隙不能被充分填充。为此,本研究团队在理论计算的基础上,通过试验修正理论熔渗压力(Infiltration Pressure)。
图73给出了Pb-Sn-10Ag-Re系固体润滑剂在800 ℃及不同熔渗压力下,真空熔渗GLPS金属陶瓷烧结体在保温保压60 min时的相对密度和残余孔隙度随熔渗压力变化的关系曲线。

图73 熔渗Pb-Sn-10Ag-Re复合润滑体时,熔渗压力对烧结体残余开口孔隙度和相对密度的影响
从图73可见,随着熔渗压力增加,复合材料的残余开口孔隙度急剧减小,相对密度显著提高;在熔渗压力增加到一定值后,残余孔隙度和相对密度的变化趋向稳定。显然,随着压力的增加,复合材料的残余孔隙度急剧减小,相对密度提高;毛细孔变小,作用阻力FC增大。由于在熔渗过程中,这种毛细孔尺度与作用阻力FC的增加是时间的函数,存在非线性关系。这种现象表明:
(1) 理论FC值只能作为熔渗压力的初始设计值,而在过程中,应通过试验确定其熔渗压力值;
(2) 在熔渗过程中,对于给定微孔结构特征的材料,其熔渗压力的极限决定了固体润滑体的填充率,超过该极限压力后,即使施加很高的压力也很难改善其填充效果。
4.3.5 熔渗温度对熔渗效果的影响
熔渗温度(Infiltration Temperature)是GLPS金属陶瓷烧结体熔渗过程的主要影响因素之一。熔渗温度过低,熔融固体润滑剂很难熔渗到烧结体孔隙之中;熔渗温度过高,则有可能使固体润滑剂挥发,甚至烧损。
图74给出了Pb-Sn-10Ag-0.3RE系固体润滑剂在5.0 MPa压力下,熔渗温度对GLPS金属陶瓷烧结体相对密度和残余孔隙度的影响。

图74 熔渗Pb-Sn-Ag-Re复合润滑体时,熔渗温度对烧结体残余开口孔隙度和相对密度的影响
由图74可以看出,随着熔渗温度的升高,复合材料的残余开口孔隙度急剧减小,相对密度显著提高。当熔渗温度升高至700~800 ℃时,复合材料的残余开口孔隙度和相对密度变化缓慢,而当熔渗温度高于800 ℃时,复合材料的残余孔隙度减小和相对密度随着熔渗温度升高均呈现相反的变化规律。
根据以上实验,本研究团队发现,熔渗温度对熔渗行为有着重要的影响。随着熔渗温度升高,熔融固体润滑剂的表面张力降低,流动性提高;同时,随着温度升高,熔融固体润滑剂与烧结体孔隙壁之间润湿角减小,润湿性增加,有助于熔渗。因此,随着熔渗温度升高,复合材料的残余孔隙度急剧减小,相对密度显著提高。但是,过高的熔渗温度,一方面会导致固体润滑剂组成元素部分氧化,使界面反应加剧,形成过多的界面反应产物,对熔渗过程产生不利影响;另一方面,随着熔渗温度的升高,熔融固体润滑剂蒸气压升高,挥发速度加快。
Pb-Sn-Ag-Re系固体润滑剂各组元的蒸气压随温度的变化值见表16[48-49]。而蒸汽压是与物质的熔点和沸点紧密相关的材料物性参量,决定了一定压力下元素挥发的速度,蒸气压越高,元素挥发的速度越快。

表16 不同温度下Pb,Sn和Ag的蒸气压值对应的温度值
由表16可以看出,当熔渗温度达832 ℃时,Pb的蒸气压达到0.1 Torr,而Sn和Ag的蒸气压仍然较低,因此,熔融固体润滑剂中部分Pb将挥发成铅蒸气,在熔融固体润滑剂中形成气泡,熔渗冷却后部分气泡未排除而残留在复合材料中,从而增加复合材料的残余孔隙度,降低复合材料的相对密度。为此,Pb-Sn-Ag-Re系固体润滑剂在真空压力下熔渗GLPS烧结体时,熔渗温度不超过800 ℃为宜。
4.3.6 熔渗时间对填充效果的影响
熔渗时间(Infiltration Time)主要影响汗腺式微孔烧结体的渗透深度和残余孔隙度。熔渗时间对于烧结体的熔渗深度和残余孔隙度的影响,不仅会导致固体润滑剂含量减少,而且会使残余孔隙区产生应力集中,降低材料的承载能力。
已有的研究表明[45],孔隙材料在熔渗过程中的熔渗深度与时间和被熔物质和孔隙半径有关。
(120)
式中,Lh为烧结体的熔渗深度;t为时间;θ为熔融固体润滑剂与金属陶瓷间的润湿角,(°);r为等效孔隙半径,mm;η0为熔融固体润滑剂的动力粘度,Pa·s。
当熔渗温度T值确定时,当γlg和θ和η0也为定值时,可计算出Lhmax;此时,若适当地延长熔渗时间,则可改善被熔物质的均匀化,减小残余孔隙度,提高烧结体中的润滑剂含量。
为了控制熔渗速率(Infiltration Velocity),可将式(120)对时间求导,得出熔渗速率与熔渗时间的关系模型。
(121)
式中,vin(t)为熔渗速率。
根据式(121),在一定熔渗温度下,选定最小熔渗速率vin(t)min,即可估算所需的熔渗时间。
图75给出了Pb-Sn-10Ag-Re系固体润滑剂在800 ℃及50 MPa压力下,真空压力熔渗GLPS金属陶瓷烧结体时,相对密度和残余孔隙度随熔渗时间变化的关系曲线。
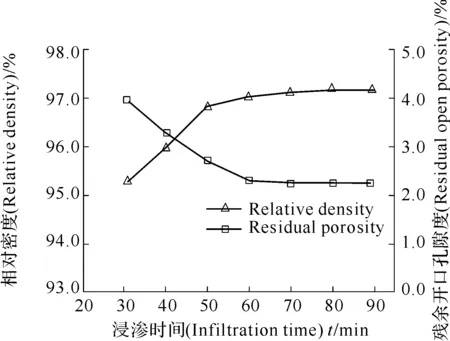
图75 熔渗Pb-Sn-10Ag-Re复合润滑体时,时间对烧结体残余开口孔隙度和相对密度的影响
从图75可以看出,随着熔渗时间延长,复合材料的残余孔隙度快速减小,相对密度急剧提高。在熔渗时间延长到50 min后,复合材料的残余孔隙度和相对密度随熔渗时间变化渐趋缓慢,至60 min后,变化曲线趋于直线。
由熔渗速率与熔渗时间的关系模型(见式(121)),熔渗速率与熔渗时间的平方根成反比,理论上熔渗时间t无最大值。熔渗开始时,熔渗速率最大,随着熔渗时间延长,熔渗速率先是快速减小,而后逐渐减缓,当熔渗时间达到一定值后,熔渗速率为一趋于零的值;同时,熔渗时间与熔渗速率的关系必须在一定的温度和压力下才能成立,较高的熔渗温度和较高的熔渗压力都有利于缩短时间。
因此,从经济性和生产效率角度观察,综合考虑熔渗温度、熔渗压力及熔渗时间对复合材料相对密度和残余孔隙度的影响,在本研究中,选择熔渗时间为60 min。
4.4 多元固体润滑体组分对填充效果的影响
由上述的熔渗工艺参数理论分析可以看出,被熔渗物质的物化性能将影响到熔渗效果,而在工程应用中,为了改善润滑性能,往往利用润滑剂的复合效应,因此,在复合过程中,多元复合润滑体组对熔渗效果的影响值得讨论。
4.4.1 Sn含量对压溃强度和残余孔隙度的影响
图76给出了Pb-Sn系固体润滑剂在600 ℃及5 MPa压力下,真空压力熔渗GLPS金属陶瓷烧结体,保温保压60 min时的压溃强度和残余孔隙度随Sn含量变化而变化的曲线。

图76 Sn(wt%)对熔渗Pb-Sn二元固体润滑剂的复合材料压溃强度和残余开口孔隙度的影响
由图76可以看出,随着Pb-Sn系固体润滑剂中Sn含量的增加,压溃强度逐渐增加,残余孔隙度逐渐减小,当Sn含量为38.1wt%时,残余孔隙度出现最小值(2.96%),同时压溃强度出现一个峰值。随着Sn含量持续增加,残余孔隙度先缓慢增加,至Sn含量为45wt%后又缓慢降低,而压溃强度逐渐减小,当Sn含量增加至Pb-Sn合金共晶成分(Pb-61.9%Sn)[50]时,残余孔隙度再次出现最小值(2.88%)。此后,随着Sn含量增加,复合材料的残余孔隙度逐渐升高,压溃强度逐渐降低。
Sn含量对压溃强度和残余孔隙度的这种影响主要来自于Sn含量对在Pb-Sn二元合金性能的影响。由Pb-Sn二元合金相图[50],随着Sn含量增加,Pb-Sn二元合金的熔点温度逐渐降低,至共晶温度183 ℃后,熔点温度又逐渐升高;600 ℃时,随着Sn含量增加,液态Pb-Sn二元合金的表面张力逐渐降低。当Sn含量达到38.1wt%时,Pb-Sn二元合金的表面张力呈现最小值(464 dyne·cm-1),随后,液态Pb-Sn二元合金的表面张力开始升高;当Sn含量达到60wt%时,呈现另一最小值(451 dyne·cm-1)。
这表明,通过控制液态Pb-Sn二元合金的表面张力,可影响其流动性;通过改变Sn含量,可调整液态Pb-Sn二元合金的表面张力,进而改变其流动性,提高汗腺式微孔材料的润滑体填充率,降低其残余孔隙度,改善熔渗质量。因此,就熔渗效率而言,选择Pb-38.1wt%Sn或Pb-61.9wt%Sn的二元合金比配比是可行的。
4.4.2 Ag对熔渗后材料的压溃强度和残余孔隙度影响
图77为Pb-Sn-Ag系润滑体在800 ℃及5 MPa压力下熔渗时,压溃强度和残余孔隙度随Ag含量变化的关系曲线。

图77 Ag质量百分含量对熔渗Pb-Sn-Ag润滑体的复合材料压溃强度和残余开口孔隙度的影响
由图77可以看出,随着Ag含量增加,熔渗后材料的残余孔隙度在Ag<2wt%前是逐渐减小,当Ag>2wt%后又逐渐增大;而压溃强度则随着Ag含量的增加逐渐增加,当Ag含量超过10wt%时,压溃强又度逐渐降低。Ag在Pb-Sn-Ag体系中对熔渗效果的这种现象与其熔点有关。
Ag在Pb和Sn中均无固溶度,但可与Sn形成Ag6Sn和Ag3Sn等两种金属间化合物。随着Ag含量的增加,Pb-Sn-Ag系固体润滑剂的熔点逐渐降低,但Pb-Sn-Ag三元体系中有一共晶点,其组成为1.35wt%Ag,36.26wt%Pb和62.39wt%Sn,共晶温度为178 ℃[51]。当Ag含量超过1.35wt%时,随着Ag含量的增加,Pb-Sn-Ag系固体润滑剂的熔点又逐渐升高。由于Ag与Pb-Sn-Ag系固体润滑剂中的Sn可以发生冶金反应,形成Ag-Sn金属间化合物,这些高熔点金属间化合物沉积在烧结体孔隙壁上,从而影响液态固体润滑剂向孔隙深度方向扩展;由于Ag的熔点比Pb和Sn高,因此,在Pb-Sn系加入Ag颗粒必然导致熔融固体润滑剂的粘度增大,降低其流动性;且增强颗粒含量越多,熔融固体润滑剂的粘度就越大,流动性越差。Ag在Ag-Sn化合物值中的上述影响也反映在本研究中。实验表明,Pb-Sn-Ag系复合润滑体中Ag含量对填充质量的影响分为以下3个区段:
(1) 当Ag<2wt%时,Ag对Pb-Sn-Ag系的润湿性影响不大[50],因此,随着Ag含量增加,熔融固体润滑剂的流动性因熔点降低而提高的程度大于因粘度增加而降低的程度,复合后的材料残余孔隙度变小;
(2) 当Ag>2wt%时,熔融Pb-Sn-Ag系固体润滑剂流动性因粘度增加而降低,复合后材料的残余孔隙度随Ag含量的增加而增加;
(3) 当Ag>10wt%时,由于过多的Ag6Sn和Ag3Sn相存在,这些固体小颗粒使得气泡逸出路线混乱,从而导致气泡逸出速度下降,使烧结体在熔渗冷却后仍有少量气泡残存于固体润滑相中,增加了材料的残余孔隙度,而使压溃强度逐渐降低。
4.4.3 Re含量对相对密度、压溃强度和残余孔隙度的影响
对于高温复合材料而言,提高多元润滑体的表面活性,不仅可改善其熔渗效率,而且可提高其在高温摩擦过程中扩散润滑性能。由于稀土及其氧化物为表面活性物质,具有较大的原子半径,在合金中的固溶度很小,而最大固溶度小的溶质在界面处被吸附的趋势大[52-53]。因此,稀土元素加入后易被吸附在晶界及界面处,起到净化界面的作用,从而降低界面能,减少了固体润滑剂晶粒长大的驱动力,可以明显细化晶粒,提高固体润滑剂相的强度;另一方面由于稀土元素的活性高,易与O和S化合,使固体润滑剂颗粒得到净化,改善元素间的润湿性,增加熔融固体润滑剂与烧结基体孔隙壁的润湿面积,促进更多的熔融固体润滑剂渗入到烧结体的孔隙中,增加复合材料的熔渗率和相对密度。
图78给出了Pb-Sn-Ag-Re系固体润滑剂在800 ℃及5 MPa压力下熔渗时,压溃强度、残余开口孔隙度和相对密度随Re含量变化的关系曲线。由图78可以看出,随着Re含量增加,熔渗后烧结体的残余开口孔隙度逐渐减小,其最小值为2.4%。但在Re含量增加到一定量后,残余孔隙度随着Re含量持续增加而逐渐增大;而压溃强度随着Re含量持续增加;相对密度也随Re含量的增加而升高,其最大值为97.1%,在Re含量增加到一定量后,相对密度随Re含量增加均降低。稀土含量对熔渗效率的这种影响,主要归结于稀土中存在的夹杂物,这些夹杂物不利于多元润滑体在熔融过程中的颗粒重排,且过多的氧化物吸附在界面处又会增加界面张力[52],反而降低熔融固体润滑剂与烧结体的润湿性,从而降低了其熔渗效率;使复合材料的残余开口孔隙度增加,熔渗率和相对密度降低。显然,稀土组分含量的设计应以试验为基础;在本研究中,综合考虑稀土氧化物对复合材料残余开口孔隙度、相对密度及压溃强度的影响,在Pb-Sn-10Ag系中加入一定量的Re较合适。

图78 Re质量百分含量对熔渗Pb-Sn-Ag润滑体的复合材料压溃强度、开口孔隙度及相对密度的影响
5 高温发汗自润滑胞体结构特征及其细观力学行为
高温发汗自润滑材料(HTSSLC)制备过程的典型工艺流程是在基体上制备出汗腺式微孔结构(GLPS),再将多元固体润滑剂填充在微孔之中,最终形成具有胞体结构特征的HTSSLC。在上述工艺流程中,GLPS是实现高温润滑功能的载体。因此,润滑胞体的功能控制机理研究有助于提高HTSSLC的性能,更可拓宽其工程应用领域。
笔者在高温发汗润滑胞体功能控制机理(Function Control Mechanicms of High Temperature Sweating Lubricating Cells,FCM-HTSSLC)细观力学分析基础上,构建起胞体材料等效弹性模量及热膨胀系数的计算模型;通过胞体形变的分析研究,探讨胞壁、胞核组分配比对胞体润滑功能的影响机理。
5.1 高温发汗自润滑胞体微观结构特征及其细观力学行为
5.1.1 高温发汗自润滑胞体微观结构特征
本研究团队制备的GLPS胞体的SEM形貌见图10。图10(a)为基体表面有序微孔,微孔的尺寸大小和分布形态取决于材料组分和制备工艺参数,其表征方法采用开口孔隙度评价;图10(b)为基体横截面形貌,其孔隙呈现出类似弯曲管的剖开形态,且互相贯通;图10(c)为剖开形态(见图10(b))的局部放大,呈现出纵横交错管状通道。这种内贯通孔和表面有序孔相交融的孔结构具有典型的人体汗腺结构特征,基于这种微孔结构可构建出具有仿生胞体形态的复合材料。
GLPS金属陶瓷烧结体汗腺式微孔中熔浸Pb-Sn多元固体润滑剂后,形成的HTSSLC横截面形貌及润滑层中润滑元素的梯度分布变化情况见图79。

图79 熔浸后材料横截面形貌(SEM×100)及Pb-Sn分布形态
由图79可以看出,HTSSLC的宏观结构由具有微孔结构的基体和具有润滑元素梯度分布的润滑层组成;由于物化特性及与基体材料界面特性不同,不同润滑元素在润滑层中具有不同的分布特性;润滑层微观结构具有简单重复的胞体材料结构特征。图80为HTSSLC润滑胞体的典型结构形态。图80中基体材料是高速钢基陶瓷,软金属润滑剂元素为Pb。

图80 复合Pb元素后的高速钢基陶瓷润滑胞体的相结构组成
由图80可以看出,在该胞体中,胞壁为Cr-Fe硬质相,胞核为Pb软质相,而胞管为耦合在软相中的Ti,W和V碳化物相。显然,这种特殊的胞体结构形态不仅使材料具有良好的耐磨功能和润滑功能,而且能通过调整胞核润滑元素与胞壁材料热膨胀系数,控制其润滑元素的析出量,从而实现其高温扩散自润滑功能,提高在极端高温环境中的摩擦副工作寿命和可靠性。
5.1.2 高温发汗自润滑胞体微观力学行为研究
基于图80的高温发汗自润滑胞体结构形态,其结构具有如下微观特征。
【特征1】 高温自润滑烧结体材料为连续孔复合体。
【特征2】 高温自润滑烧结体材料由不同组分的硬质相基体和软质相胞核组成。
【特征3】 硬质相基体为颗粒增强复合材料。
【特征4】 软质相胞核为多相金属组成的复合材料。
取图80中的任意一个润滑组元进行微胞热应力分析(Thermal Stress Analysis)。在热应力(摩擦温度)作用下,材料的组织结构将发生体积变化。受热时,材料中的各相均会膨胀,各相之间会产生内应力。软质相胞核将受到来自硬质相胞壁的压应力σM;同时,硬质相胞壁也同样受到了软质相胞核的压应力σTC。
当
σM=σTC
(122)
时,应力相互抵消,将引起整个体积的膨胀。
当
σM-σTC>τ
(123)
时,固体润滑剂将能够从中析出。式中,τ为固体润滑剂剪切应力。
图81为胞体结构微观示意,图中胞体结构材料由基体颗粒Ⅰ和胞核固体润滑剂颗粒Ⅱ组成,基体为金属基陶瓷相(例如,TiC-Fe-Cr-W-Mo-V)(也称为基体硬质相);胞核为由软金属组成的复合固体润滑剂(例如,Pb-Sn-Ag-Cu)(也称为胞核软质相)。

图81 胞体结构微观示意
【假定1】 该润滑胞体的硬质相和软质相均为均质材料。
则其弹性模量、膨胀系数等微观力学参数对HTSSLC在高温下的机械及润滑性能有着重要的影响。
5.2 HTSSLC等效弹性模量的计算
HTSSLC基体为颗粒增强型复合相,采用拉伸应力-应变试验(Tensile Stress Versus Strain Experiment)很难确定其弹性模量,特别是在摩擦接触过程中,其微塑性使材料的应力-应变曲线过早偏离弹性变形范围,故常采用等效弹性模量法则(Equivalent Elastic Modulus Principle,EEMP)进行计算。但EEMP对于同时具有应力和应变的多相胞体结构材料(Multi-Phase Cellular-Structure Material)的弹性模量计算非常复杂。
本研究团队设定复合材料中各相组分在等效弹性模量计算中的体积比例为αV,将αV引入Hirsch模型(Hirsch Model),推导出适应多相润滑胞体材料的弹性模量修正Hirsch模型(Modified Hirsch Model of Elastic Modulus,MHMEM)。
5.2.1 Hirsch模型
为了计算多相复合材料的弹性模量,Voigt和Reuss分别提出了等应变模型及等应力模型[54-55]。两相复合材料的等效弹性模量可表示为如下形式。
EV(ξ)=Eαξα+Eβξβ
(124)
(125)
式中,ξα为α相在复合材料中所占体积含量;ξβ为β相在复合材料中所占体积含量;Eα为α相弹性模量;Eβ为β相弹性模量;EV(ξ)为Voigt等应变模型的弹性模量;ER(ξ)为Reuss等应力模型的弹性模量。
多相复合材料的微观结构中不仅存在着Voigt等应变模型,也存在Reuss等应力模型,这两种方式的不同结合形式及比例就构成了实际复合材料的结构。在EV(ξ)和ER(ξ)的计算中(见式(124)和(125)),Voigt模型和Reuss模型分别给出了复合材料等效弹性模量值的上限和下限,产生了较大的误差。为此,研究人员提出了一种Hirsch模型[56],将两相间的应力与应变进行组合(见图82,箭头所示纵向作用力方向)。

图82 由等应力和等应变组合而成的Hirsch Model
这样,当模型应力方向为纵向时,复合材料的Hirsch模型的等效弹性模量
(126)
式中,αV为Voigt等应变模型在混合模型中所占的体积比例;V11为α相在Reuss模型中所占体积含量;V12为β相在Reuss模型中所占体积含量;V21为α相在Voigt模型中所占体积含量;V22为β相在Voigt模型中所占体积含量。
5.2.2 因子αV的计算
显然,合理选择比例因子αV,可有效地提高效弹性模量的计算精度。对于具有多相胞体结构HTSSLC,αV因子可表示为如下形式[57]:
(127)
式中,ξi为第i个样本α相的体积含量;φ1(ξi)为第i个样本Voigt模型与Reuss模型得到的等效弹性模量倒数之差;k(ξi)为复合材料等效弹性模量试验值的倒数;φ2(ξi)为第i个样本Reuss模型得到的等效弹性模量倒数;EV(ξi)为第i个样本基于等应变模型(Voigt模型[54])的两相(α相和β相)复合材料等效弹性模量;ER(ξi)为第i个样本等应力模型(Reuss模型[55])计算的两相(α相和β相)复合材料等效弹性模量。
式(126)为半经验公式,αV需要根据实验数据模拟得到,对实验测量依赖性较高,因此并不太容易用于实际预测当中。
基于此,本研究团队提出一种αV因子的改进算法。由于弹性模量计算仍以图82为基础,仅在算法上引入αV因子,因此,该弹性模量计算模型称之为修正Hirsch模型(MHMEM)。
5.2.3 弹性模量修正Hirsch模型(MHMEM)
假设微观无限大两相复合材料中的微元体是均匀和各向同性的。图83(a)为两相复合材料的简单模型,基体相和夹杂相的接触方式分为接触方式1、接触方式2和组合方式3(见图83(b)),其中组合方式3为接触方式1和接触方式2的组合。该微元体分别由一定比例满足等应力和等应变边界条件的相相界面所组成,因此可以按照统计规律将复合材料组合(见图83)。

图83 复合材料简单模型
对于各向异性材料,其等效弹性模量计算见式(126)。对于实际的颗粒增强复合材料,由于内部颗粒排列的随机性,其材料性质表现为各向同性。因此,本研究团队将从横向和纵向等两个方向考虑其等效弹性模量(见图84)。

图84 修正Hirsch方法
根据图84的约定
V11/V12=V21/V22=ξα/ξβ
(128)
当应力方向为水平方向(见图84)时,该方向上的等效弹性模量可表示如下。
E1=EV=ξαEα+ξβEβ
(129)
式中,Et为复合材料等效弹性模量;E1为由V11和V12组成的复合体的Voigt等应变模型的等效弹性模量;E2为由V21和V22组成复合体的Reuss等应力模型的等效弹性模量。
由式(129)可以得到两相复合材料的等效弹性模量计算模型。
(130)
对于颗粒增强复合材料,其材料性质在宏观上表现为各向同性,满足EH=Et。根据式(126)和式(130),可以得到αV的表达式。

ke=ER/EV
(131)
式中,ke为复合材料通过Reuss模型和Voigt模型计算得到的等效弹性模量比。
式(131)中,当ke=1时,由ER和EV的表达式可以推导出Eα=Eβ,即α相和β相为同一介质或两相具有相等弹性模量的介质,此时等效弹性模量与各相所占体积含量无关,因此αV与ke取值无关,可取0~1范围内任何值。
将式(131)引入Hirsch模型中,则颗粒增强复合材料的等效弹性模量
(132)
式(132)基于两相颗粒增强复合材料而得到。对于由多相组成的颗粒增强复合材料,其计算模型与式(132)相同,此时
EV=∑ξiEi
(133)
ER=∑ξi/Ei-1
(134)
式中,ξi为颗粒复合材料中第i相成分的体积含量;Ei为颗粒复合材料中第i相成分的弹性模量。
αV的物理意义为微元体中满足等应变边界条件的体积与微元体总体积的比值。对于各相体积含量一定的颗粒增强复合材料,各相的结合与排列方式在微观结构上随机分布,但颗粒增强复合材料材料性质在宏观上表现为各向同性。由式(131)可知,αV不但与颗粒复合材料中各相的弹性模量有关,而且与各相成分的体积含量有关,从而解决了复合材料计算中弹性模量与其相成分相关联的理论问题。
5.2.4 模型精度验证
为了验证本研究团队提出的修正Hirsch模型的精度,选用文献[58]中的试验数据进行比较性验证。
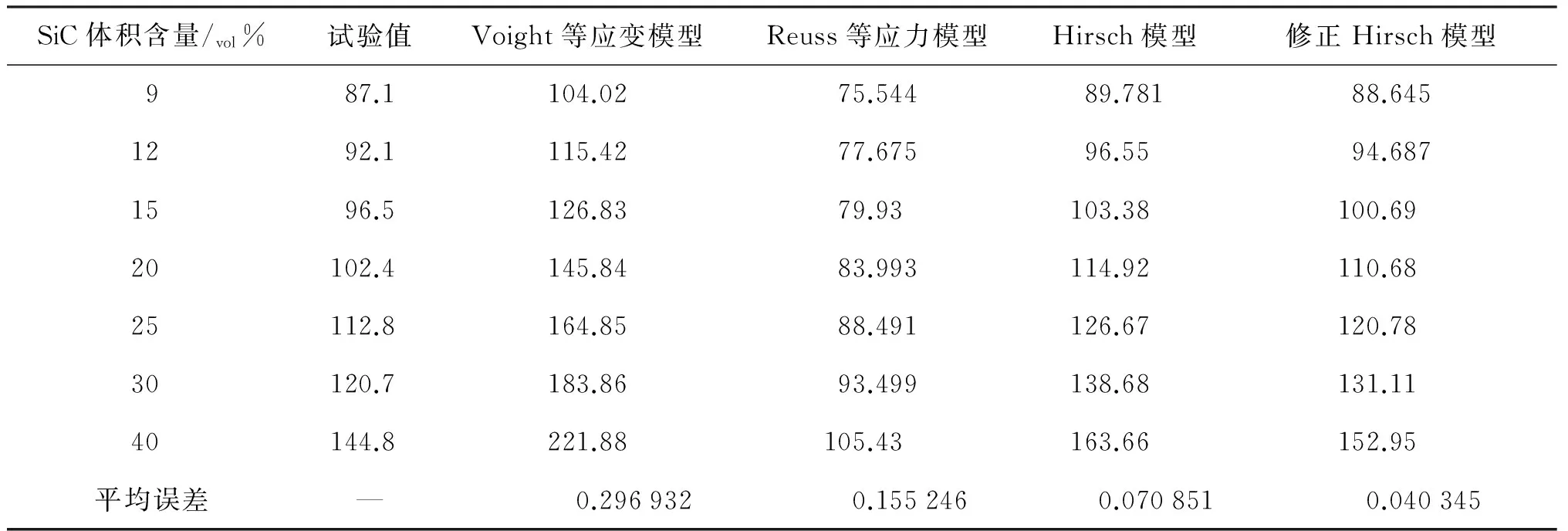
【算例1】 在文献[58]中的复合材料选用了6066合金及平均粒度为7~12.6 μm的SiC颗粒,选用喷射共沉积法(spray Co-deposition method)制备出颗粒增强6066/SiC铝基复合材料,利用动态模态测试仪测量出生成的复合材料弹性模量(见表17)。

表17 6066/SiC复合材料试验值与各种模型预测值/GPa[58]
续表
根据式(131)可以求得SiC成分不同体积含量下的αV,颗粒增强复合材料的等效弹性模量可以根据式(132)计算得到Voigt模型、Reuss模型和Hirsch模型的等效弹性模量(见表17和图85),其中Hirsch模型中的αV根据经验取值为0.4[54]。
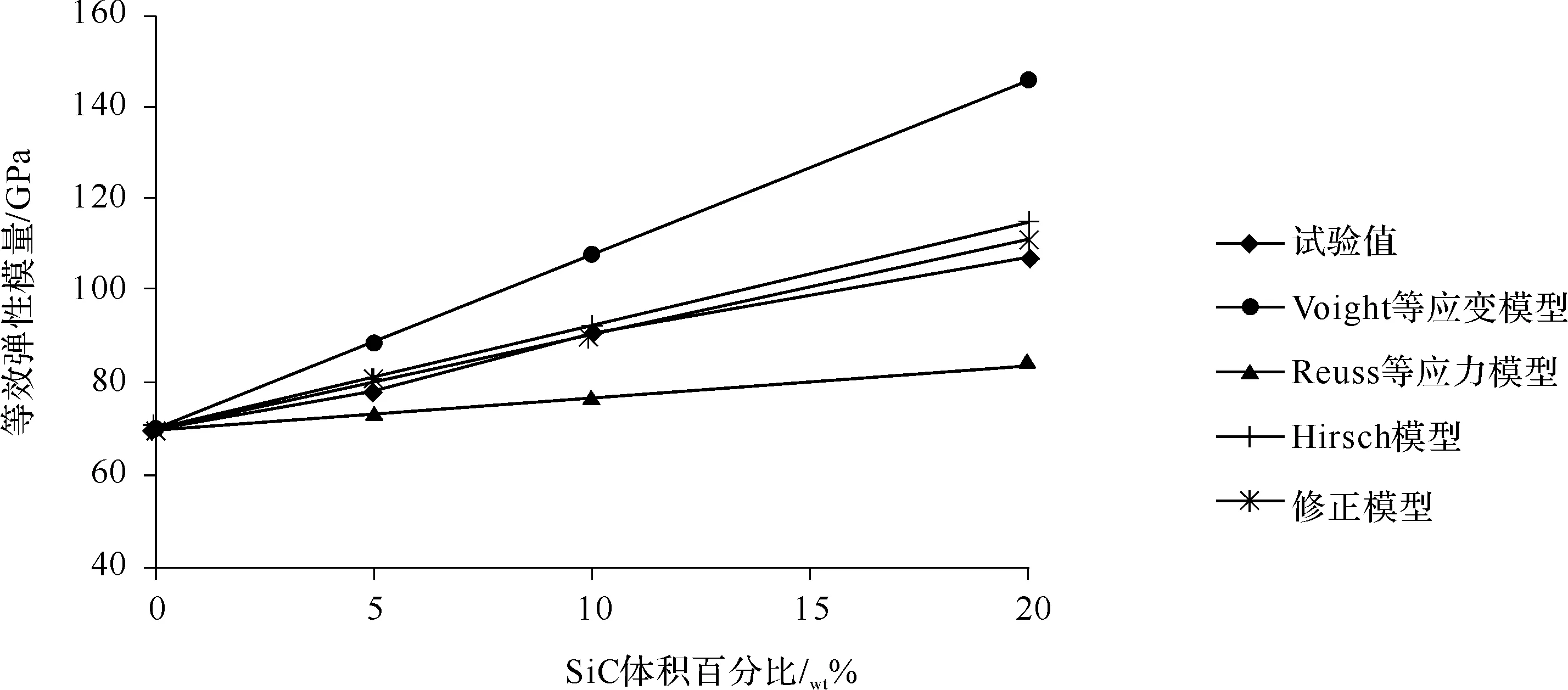
图85 SD法6066/SiC弹性模量的计算值与试验值比较
从表17和图85可知,修正Hirsch模型的计算结果处于Voigt等应变模型的上限值和Reuss等应力模型的下限值之间,较Hirsch模型更加接近试验值,并且理论计算值与试验值之间具有较好的一致性,特别是在SiC的体积含量较小时(≤15%),理论结果与试验结果几乎相同(相对误差<5%),当SiC的体积含量增大时(>15%),理论计算结果稍大于试验结果,这是由于实际的6066/SiC铝基复合材料浸渗不完全而造成的,在颗粒与颗粒接触的区域、颗粒的尖角处存在气孔,这与李进军等学者[59]的试验结果分析相一致——由于气孔的存在,造成了理论值高于试验值的状况。
【算例2】 采用Al/30nmSiC颗粒增强材料[59],其等效弹性模量试验值见表18。

表18 Al/30nm SiC颗粒增强材料弹性模量
利用基于αV因子算法,其等效弹性模量见表19。为进行比较,采用Voigt等应变模型,Reuss等应力模型,Hirsch模型和修正Hirsch模型分别计算不同SiC体积含量下的Al/30nmSiC的等效弹性模量,计算结果见表19。
由表19可知,修正Hirsch模型计算结果处于Voigt模型上限和Reuss模型下限之间;修正后,Hirsch模型的平均误差为1.5%,仅为传统Hirsch模型的50%。因此,修正Hirsch模型可有效地应用于复合材料微弹性模量计算。

表19 试验值与各种模型预测值
5.3 颗粒增强型均质复合材料热膨胀系数计算模型
复合材料中各相成分的力学性质各不相同,各相成分的力学性质将最终影响到复合材料的整体力学性质。基于HTSSLC的润滑机理,热膨胀系数是保证其润滑性的一个非常重要的设计参数[60]。为此,本研究团队讨论了HTSSLC硬质相和软质相的热膨胀系数,建立了一种不必区分增强相和基体相的简单算法,可精确预测多相均质复合材料的线性热膨胀系数(linear coefficient of thermal expansion)。
迄今为止,复合材料热膨胀系数计算模型(Model of Predicting the Thermal Expansion Coefficient of Composites,MPTECC)大多是基于线性混合法则(linear combination law)建立的。虽然线性混合法则认为复合材料的热膨胀系数与各相体积比及各相线性热膨胀系数相关,但其前提是忽略组元间的相互作用[61-62]。显然,基于线性混合法则建立的MPTECC不适用于胞壁和胞核材料性能具有明显差异的HTSSLC的热膨胀系数计算。
为此,本研究团队以多组分混合增强相为基础,建立了颗粒增强型均质复合材料热膨胀系数计算模型(Thermal Expansion Coefficient Model of Particle Reinforced Composites,TECMPRC)。为了便于分析,首先进行如下假设。
【假设9】 增强颗粒和基体粉末颗粒在复合材料中均匀分布,颗粒呈球形(见图86)。

图86 复合材料微结构假设示意
由图86可以看出,当任选一颗粒时,该颗粒处于基体颗粒与增强颗粒相之中,若考虑材料中增强相(基体)之间的相互影响,以及增强相对基体的作用,假设增强相和基体分别嵌于复合材料中,同时取其中一个颗粒和它周围的复合材料为研究对象,则可得到单胞模型(Homocentric Sphere Model,HSM)(见图87)。
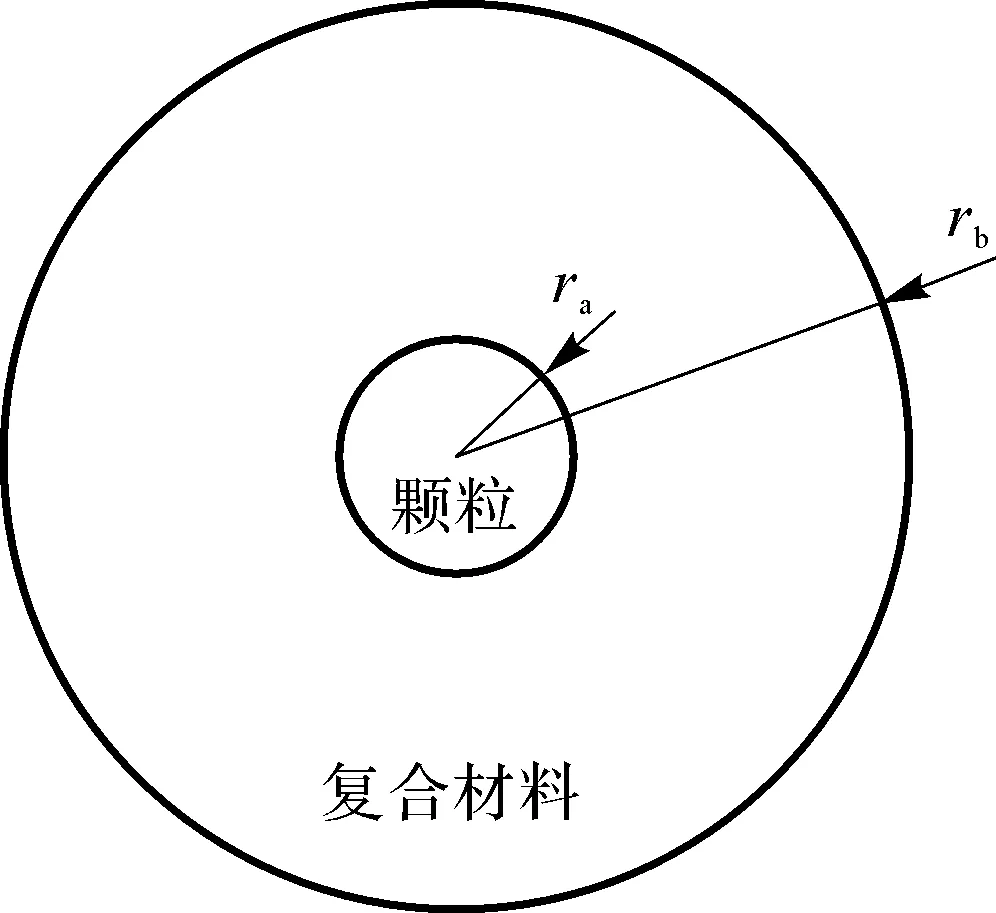
ra为颗粒半径,rb为复合材料的半径;ra≪rb
根据复合材料各相细观体积热膨胀量与宏观体积热膨胀量相等的原则,利用热弹性力学方法可推导出复合材料热膨胀系数。
5.3.1 细观热应力分析
一般地,复合材料的热膨胀系数和颗粒的热膨胀系数不相等。当复合材料的环境温度发生改变时,颗粒和复合材料的热胀冷缩产生的变形将会不一致,从而导致产生热应力;在热应力作用下,颗粒会出现相应的应变,因此,颗粒在复合材料中的约束热膨胀系数(thermal expansion coefficient under constraints)与颗粒本身的热膨胀系数是不一样的。本研究团队通过分析单个颗粒的热应力,求解颗粒在复合材料中的约束热膨胀系数。
【假设10】 颗粒、复合材料在讨论的温度区间内表现为各向同性弹性体,它们的本构关系分别满足广义胡克定律。
在由热膨胀差异形成的界面径向作用力作用下,复合材料在界面处满足位移和应力连续性条件如下
(135a)
(135b)
式中,urc为复合材料的径向位移;urp为颗粒的径向位移;p为由热膨胀差异形成的界面径向作用力;σrc为复合材料的径向应力;σrp为颗粒的径向应力。
由热弹性力学的相关知识[60],可以得到界面处颗粒的位移
(136)
式中,urp为颗粒径向位移;αp为颗粒的线膨胀系数;′T为复合材料相对于无内应力的初始温度的温差;Kp为颗粒的体积模量。
强颗粒内的平均应力
(137)
式中,σtp为颗粒切向应力。
强颗粒内的平均应变

(138)
复合材料在界面处的位移
(139)
式中,αc为颗粒的线膨胀系数;Gc为复合材料的剪切模量;ra为颗粒半径。
由连续性边界条件(见式(135)),可以解得
(140)
式中,αp为颗粒的线膨胀系数。
而颗粒的平均应力σp=-p,因此
(141)
5.3.2 颗粒的约束热膨胀系数
颗粒的平均应变由受热应力作用下的应变和热膨胀应变等两部分组成,将这两种应变等效为约束热膨胀应变,与之相对应的热膨胀系数就是约束热膨胀系数。将颗粒的平均应力(见式(137))代入到增强颗粒的平均应变模型(见式(138))中,可以得到
(142)

5.3.3 均质复合材料热膨胀系数计算模型
由上述分析知道,复合材料的平均应变εc=αcT′。若复合材料有n相,由细观力学[63]可知

(143)

由式(143),可以得到复合材料的热膨胀系数
(144)
式中,ξi为第i相组分的体积含量;i=1,2,…,n。
由式(142),可以得到
(145)
式中,Ki为第i相体积模量;i=1,2,…,n。
由式(144)和式(145),可得到复合材料的热膨胀系数
(146)
式中,Ec为复合材料的等效弹性模量;νc为复合材料的等效泊松比。
复合材料的弹性模量可采用的Hirsch模型的αV因子改进算法进行计算[64]。
(147)
可以看出,式(146)推导的复合材料热膨胀系数的最大特点是不必区分增强相和基体相,特别是在一些混合相为中等体积分数时,很难区分基体相和增强相,若取不同的材料为基体相时预测会出现不同结果,因此偏差较大,而本算式不必区别基体相和增强相。对于只有一种增强相的两相材料,只需令n=2即可。
5.3.4 TECMPRC的验证
为了验证TECMPRC的正确性,本研究团队选取两种复合材料进行验证。
【算例3】 第一种材料选取复合材料Sip/LD11[65];在Sip/LD11中,增强体为高纯Si颗粒,基体为LD11铝合金,采用挤压铸造法(squeeze casting method)制备出增强体含量分别为55%,60%和65%的复合材料,各相组元的力学参数和物理参数见表20。

表20 Sip/LD11、Diamond/Copper复合材料组元参数[66]
为了比较TECMPRC的预测精度,本研究团队分别计算了Kerner预测模型预测值[67]和Turner[68]预测模型预测值,并进行了比较,其中Turner预测模式如下。
(148)
式中,αm为第m相材料的热膨胀系数;Km为第m相材料的体积模量;Vm为第m相在复合材料中的体积含量;αp为第p相材料的热膨胀系数;Kp为第p相材料的体积模量;Vp为第p相在复合材料中的体积含量。
Kerner预测模型如下。
(149)
式中,Gm为第m相材料的剪切模量。
最终,TECMPRC的计算值、Turner预测模型的预测值、Kerner预测模型的预测值,以及实验值见图88。

图88 不同模型下的热膨胀系数预测值与实验值关系曲线
从图88可以看出,TECMPRC的计算值处于Turner预测模型的预测值和Kerner预测模型的预测值之间,与实验值之间的误差最小,能够较好的符合试验结果。
【算例4】 第二种材料选取铜合金为基、diamond混合粉末为增强颗粒,制备出了增强体含量为10%~40%的试样,两种材料组元的物理参数和力学性质见表21。

表21 Sip/LD11、Diamond/Copper复合材料组元参数[69]
图89为Diamond/Copper复合材料材料在不同预测模型下的热膨胀系数预测值与实验值的比较。从图89可以看出,TECMPRC的预测值处于Kerner预测模型和Turner预测模型的预测值之间,计算结果与实验结果也较符合。

图89 不同模型下的热膨胀系数预测值与实验值关系曲线
算例3和算例4的计算结果表明,本研究团队建立的TECMPRC预测值处于Turner模型和Kerner模型的预测值之间,能够较好的预测复合材料热膨胀系数,而且不需要区分基体相和增强相。这在预测一些基体相和增强相均具有中等体积分数因而很难加以区分的复合材料热膨胀系数时,保证了预测的准确性,为具有胞体结构的HTSSLC的润滑性能研究提供了理论基础。
5.4 胞体材料细观力学性能
5.4.1 胞壁材料细观力学性能
HTSSLC的基体由金属陶瓷相组成(基体硬质相)。TiC-Fe-Cr-W-Mo-V基体的弹性模量对HTSSLC的润滑相在摩擦过程中析出有重大影响。因此,建立均质复合材料等效弹性模量预测模型(Prediction Model of Equivalent Elastic Modulus,PMEEM),探讨硬质相中各材料组分(例如,TiC,Fe,Cr,W,Mo,V)对基体硬质相弹性模量的影响,可为GLPS材料的胞体应力应变分析提供理论基础。
GLPS材料的基体硬质相由金属陶瓷基复合材料组成,选用具有一定粒度配比的Fe-Cr-W-Mo-V合金和TiC陶瓷粉末基体。其中,TiC所占体积分数为20%,金属粉末中Cr,W,Mo,V,Fe按质量比组成,各组份的物理和机械性能见表22。
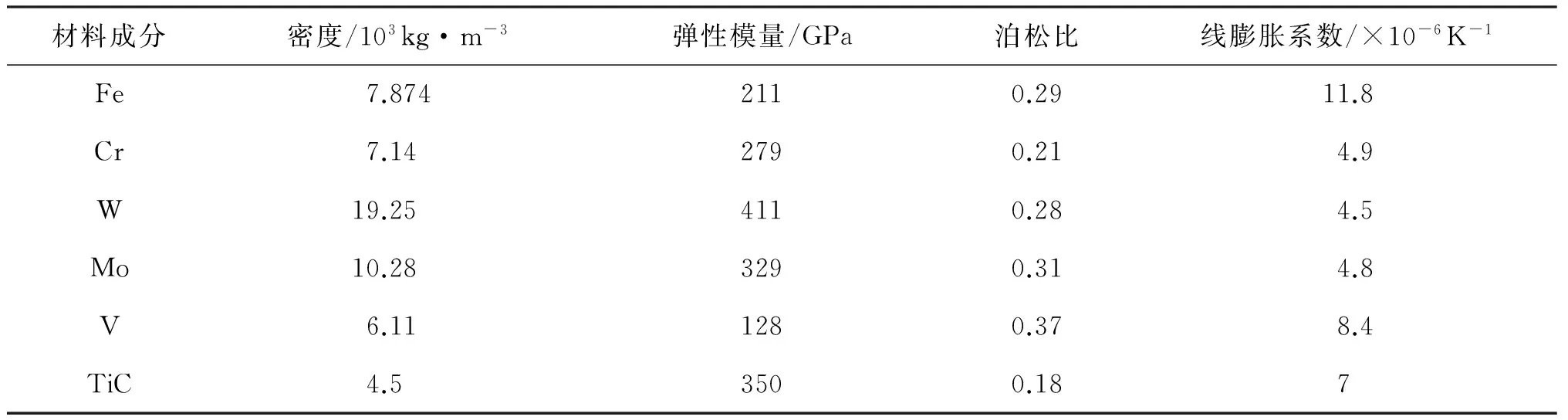
表22 金属陶瓷基复合材料各相物理机械性能[70]
根据表22提供的材料密度,可以计算得到各组成成分的体积比(见表23)。

表23 基体硬质相各组成成份的体积比
5.4.1.1 等效弹性模量计算
为了研究各组分体积含量对基体硬质相等效弹性模量的影响,分别改变某组分的体积含量(0vol%~100vol%),而其他各组分体积相对比例保持表23的所定比例。例如,当TiC的体积含量为60vol%时,Fe,Cr,W,Mo和V的体积含量分别为3.45vol%,6.65vol%,3.5vol%,8.6vol%,17.8vol%,其相对比值保持为6.9∶13.3∶7.0∶17.2∶35.6。根据修正Hirsch模型的等效弹性模量计算公式,可以求得基体中各组分不同体积含量下的等效弹性模量,其计算结果见表24和图90。
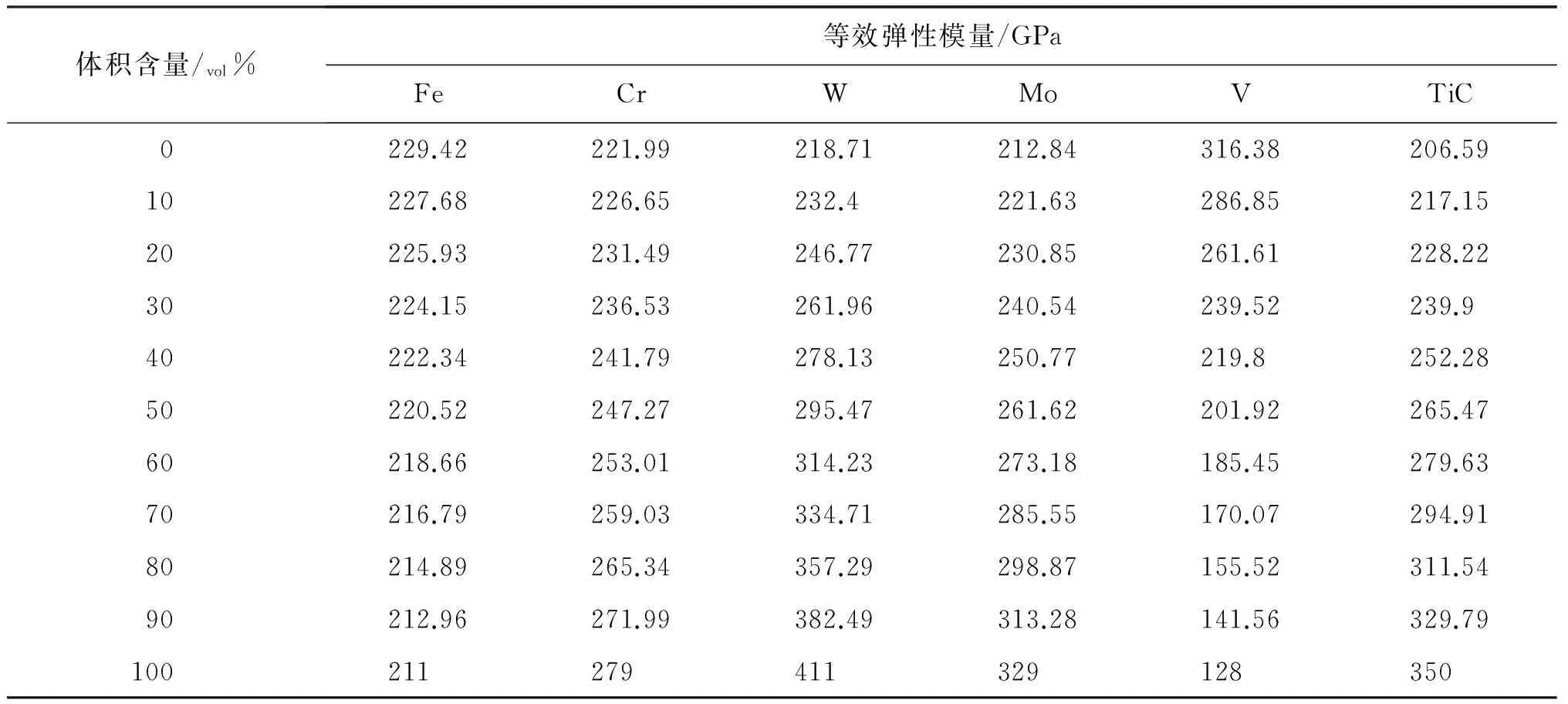
表24 基体各组分不同体积含量下的基体等效弹性模量

图90 基体硬质相中各组分不同体积含量时的基体等效弹性模量
从图90可以看到,随着Cr,W,Mo,Tic在基体硬质相中的体积含量的增加,基体硬质相的等效弹性模量呈现上升的趋势,而基体硬质相的等效弹性模量随着Fe和V在基体硬质相中的体积含量的增加而减少。根据等效弹性模量的计算模型公式可知,均质复合材料的等效弹性模量会随着复合材料中的弹性模量较大的组分的体积含量增加而增大,随着复合材料中的弹性模量较小的组分的体积含量增加而减小,如果基体硬质相中各组分按照原始比例配比,即TiC所占体积分数为20vol%,金属粉末中Cr,W,Mo,V,Fe按一定质量比组成,在此情况下,基体硬质相的等效弹性模量计算值为228 GPa,对比表24中的基体硬质相中各组分的物理属性和力学属性可知,Fe和V的弹性模量在各组分中是最小的,而且小于228 GPa,因此,随着Fe和V在基体硬质相中的体积含量的增加,基体硬质相的等效弹性模量将会减小;而Cr,W,Mo和Tic的弹性模量相对于Fe和V的弹性模量较大,并且大于228 GPa,因此,随着Cr,W,Mo和Tic在基体硬质相中的体积含量的增加,基体硬质相的等效弹性模量将会增加。
5.4.1.2 等效热膨胀系数计算
根据TECMPRC,可以得到HTSSLC的基体硬质相的等效膨胀系数(equivalent thermal expansion coefficient)(见表25和图91)。

表25 基体各组分不同体积含量下的基体等效线膨胀系数

图91 基体硬质相中各组分不同体积含量时的基体等效线膨胀系数
从图91可以知道,随着Fe,V和Tic在基体硬质相中的体积含量增加,基体硬质相的等效线膨胀系数呈现上升的趋势;而基体硬质相的等效线膨胀系数随着Cr,Mo和W在基体硬质相中的体积含量的增加而减少。根据等效线膨胀系数的计算模型,均质复合材料的等效线膨胀系数会随着复合材料中的线膨胀系数较大的组分的体积含量增大而增大,随着复合材料中的线膨胀系数较小的组分的体积含量增加而减小,如果基体硬质相中各组分按照原始比例配比,即TiC所占体积分数为20vol%,金属粉末中Cr,W,Mo,V,Fe按一定质量比组成,在此情况下基体硬质相的等效线膨胀系数计算值为6.91×10-6K-1,对比表25的基体硬质相中各组分的物理属性和力学属性,Cr,Mo和W的弹性模量在各组分中是较小的,并且其对应的线膨胀系数均小于原始比例配比的基体硬质相等效线膨胀系数(6.91×10-6K-1),因此,随着Cr,Mo和W在基体硬质相中体积含量的增加,基体硬质相的等效线膨胀系数将会减小;而Fe,V和TiC的线膨胀系数值较大,因此随着Fe,V和Tic在基体硬质相中体积含量的增加,基体硬质相的等效线膨胀系数将会增加。
5.4.2 胞核软质相材料细观力学性能
固体润滑剂选用Pb-Sn-Cu-Ag系浸渍型固体润滑剂,按质量比3∶20∶47∶30将粒度处于5~15 μm的Pb粉末,Sn粉末,粒度为6~8 μm的Cu颗粒,以及粒度为1~2 μm的Ag粉末通过机械混合30 min得到,各组成成分的物理机械性质见表26。
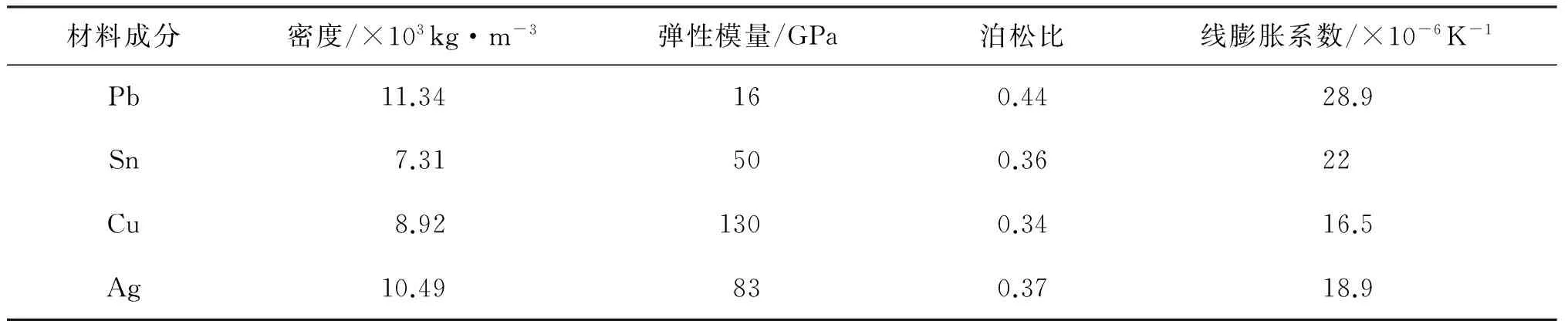
表26 固体润滑剂各组分物理机械性能[39]
固体润滑剂的弹性模量可以利用MHMEM得到,而固体润滑剂的热膨胀系数通过TECMPRC计算。
由各组分的密度,利用质量和体积计算公式可得到各组分的体积比(见表27)。

表27 固体润滑剂各组成成份的体积含量
5.4.2.1 软质相等效弹性模量计算
对于HTSSLC,可以得到其等效弹性模量(见表28和图92)。从图92可以知道,随着Cu在固体润滑相中的体积含量的增加,固体润滑相的等效线膨胀系数呈现上升趋势;而固体润滑相的等效弹性模量随着Sn和Pb在固体润滑相中的体积含量的增加而减少;随着Ag在固体润滑相中的体积含量的增加虽然有略微下降,几乎保持不变。

表28 固体润滑相各组分不同体积含量下的胞核等效弹性模量

图92 固体润滑相相中各组分不同体积含量时的胞核等效弹性模量
根据等效弹性模量计算模型可知,具有硬质相与软质相均质复合材料的等效弹性模量,随着复合材料中的弹性模量较大的组分的体积含量增大而增大,随着复合材料中的弹性模量较小的组分的体积含量增加而减小。如果固体润滑相中各组分按照原始比例配比,即固体润滑剂选用的Pb-Sn-Cu-Ag系浸渍型固体润滑剂,按质量比3∶20∶47∶30组成,在此情况下固体润滑相的等效弹性模量计算值为85.3 GPa,对比表28固体润滑相中各组分的物理属性和力学属性,Cu的弹性模量(130 GPa)在各组分中是最大的,并且只有其对应的弹性模量大于原始比例配比的固体润滑相的等效弹性模量(85.3 GPa)。因此,随着Cu在固体润滑相中的体积含量的增加,固体润滑相的等效弹性模量将变大;而Sn和Pb的弹性模量(Sn为50 GPa,Pb为16 GPa)较小,随着Sn和Pb在固体润滑相中的体积含量的增加,固体润滑相的等效弹性模量将会减小;对于组分中的Ag,其弹性模量(83 GPa)接近于由原始比例配比的固体润滑剂的等效弹性模量(85.3 GPa)。因此,随着其在固体润滑相中的体积含量的增加,固体润滑相的等效弹性模量几乎保持不变。
5.4.2.2 软质相等效膨胀系数计算
根据TECMPRC,可得到HTSSLC的基体和软质相的微膨胀系数(见表29和图93)。

表29 固体润滑相各组分不同体积含量下的胞核等效线膨胀系数

续表

图93 固体润滑相中不同组分体积比的胞核等效线膨胀系数
从图93可以看出,随着Pb和Sn在固体润滑相中体积含量的增加,固体润滑相的等效线膨胀系数呈现上升的趋势;固体润滑相的等效线膨胀系数随着Cu在固体润滑相中体积百分比的增加而减少;随着Ag在固体润滑相中的体积含量的增加虽然有略微上升,几乎保持不变。根据TECMPRC可知,具有硬质相与软质相均质复合材料的等效线膨胀系数会随着复合材料中的线膨胀系数较大组分的体积含量增大而增大,随着复合材料中的线膨胀系数较小的组分的体积含量增加而减小。如果固体润滑相中各组分按照原始比例配比,即Ag-Cu-Pb-Sn系浸渍型固体润滑剂按质量比30∶47∶3∶20组成,在此情况下固体润滑相的等效线膨胀系数计算值为18.46×10-6K-1,对比查看固体润滑相中各组分的物理和力学属性(见表29),Pb和Sn的线膨胀系数(Pb为28.9×10-6K-1,Sn为22×10-6K-1)在各组分中是最大的两个,并且大于原始比例配比的固体润滑相的等效线膨胀系数(18.46×10-6K-1),因此,随着Pb和Sn在固体润滑相中的体积百分比的增加,固体润滑相的等效线膨胀系数将变大。而Cu的线膨胀系数(16.5×10-6K-1)最小,并且小于原始比例配比的固体润滑相等效线膨胀系数(18.46×10-6K-1),因此随着Cu在固体润滑相中的体积含量的增加,固体润滑相的等效线膨胀系数将会减小;对于组分中的Ag,其线膨胀系数(18.9×10-6K-1)稍大于且非常接近由原始比例配比的固体润滑剂的等效线膨胀系数(18.46×10-6K-1),因此,随着其在固体润滑相中的体积含量的增加,固体润滑相的等效线膨胀系数虽有上升但是几乎保持不变。
上述研究表明,由于HTSSLC的特殊结构,其微观力学行为取决于相结构,当引入反映各相组分在效弹性模量中的因子αV后,能基于Hirsch模型很好地预测其等效弹性模量及相应的热膨胀系数。
5.5 HTSSLC组分元素析出特性
5.5.1 胞体形变分析模型
由TECMPRC的汗腺式微孔胞体结构出发,可简化润滑体析出分析模型(Analysis Model of Lubricant Output,AMLO)(见图94)。在AMLO中,胞壁由大小相同的球形硬质相(Fe-Cr-W-Mo-V合金和TiC陶瓷粉末基体)组成,软质相胞核由造孔剂和固体润滑剂(Ag-Cu-Pb-Sn)组成;软质相胞核被硬质相胞壁包覆,每个胞壁同时为相邻的6个软质相胞核所共有;胞壁间具有宽度为a′的距离;在高温摩擦过程中,胞核中的润滑元素在热-应力作用下沿此胞管析出。

图94 胞体微孔胞体结构尺寸示意
【假定2】 模型中球形胞壁的平均半径为Rc,若k=Rc/a′,则可得到胞核(固体润滑相)在胞体中所占的体积含量
(150)
若已知φ,则
(151)
为了提高润滑性能,选用Pb-Sn-Cu-Ag系复合组分设计,按质量比3∶20∶47∶30将粒度为5~15 μm的Pb和Sn粉末和粒度为6~8 μm的Cu颗粒及粒度为1~2 μm的Ag粉末通过机械混合30 min,再通过真空熔浸工艺复合在胞体微孔中。胞核及胞壁的弹性模量取决于各自的组分,胞核及胞壁的热膨胀系数也取决于各自的组分,其值由式(146)计算,计算时固体润滑相的各相物理及机械性能见表26,陶瓷基体相的各相物理及机械性能见表22。
表30列出了通过式(146)计算得到的胞体组元的润滑相胞核和硬质相胞壁的属性,其中润滑相和硬质相的热传导系数分别为54 W·(m·K)-1和35 W·(m·K)-1[71]。

表30 胞体组元(胞壁和胞核)的物理及机械性能
根据上述胞体结构形态及其设计参数,考虑其对称性和球形胞壁的共有特性,可建立胞体结构有限元分析模型(finite element model)(见图95)。胞体组元采用自底而上的建模方式进行网格划分,以确保网格的对称性与一致性。考虑到截面尺寸较小,为了方便运算采用plane55二维热实体单元,加载温度为200 ℃。温度场分析后通过单元转换为二维结构实体单元(plane42)进行热应力和应变分析。

图95 胞体组元网格划分及边界
基于该润滑胞体的结构特点及胞壁热膨胀系数小于胞核(约为1/3)的事实,分析时,限制胞壁外边界上节点的法向位移,而不限制其胞核的自由度(见图95),得胞元位移和等效应力(见图96和97)(材料参数见表30,孔隙度为25%)。

图96 胞元在200 ℃下的位移(mm)

图97 胞元在200 ℃下等效应力(Pa)
由图96和图97可知,胞元的最大位移都出现在胞核孔隙的外边界中心,说明胞体贯通孔结构有利于固体润滑剂的析出,胞元最大等效应力出现在胞壁的中心和胞核与胞壁的接触处,这是由于胞核和胞壁线膨胀系数存在较大差异,当温度升高时产生较大的热应力。胞核AB段节点的位移量见图98。

图98 胞核在y方向的变形(析出)位移量
由图98胞核变形量,可看出胞核沿宽度方向的变形量近似可看作二次曲线f(x),沿y方向(坐标向上)最大变形为U0。U0可以用来表征具有胞体结构微孔材料的润滑特性,在相同的温度上升条件下,如果U0越大,表示该材料的润滑能力越强,反之,润滑能力则越小。可以计算出胞核变形截面积——该二次曲线所包覆的面积。
(152)
假设温度上升后析出的胞核润滑剂能够均匀地覆盖于材料的表面(见图97的胞体底面),则在具有润滑胞体结构材料表面形成润滑膜厚度
(153)
可将润滑膜厚度t表示为孔隙度ψ的函数。
(154)
5.5.2 胞体组分及含量对胞核变形(润滑体析出)量的影响
为了研究胞核中各组分的体积含量对于胞核变形(润滑析体出)的影响,选取Pb,Sn,Cu和Ag作为组分元素。分别采用式(146)和式(154)计算不同润滑剂组分含量对胞核变形量及润滑膜铺展厚度的影响,其结果见图99和图100。

图99 胞核中润滑元素组分含量对胞核变形的影响

图100 胞核中润滑元素组分含量对润滑膜厚值的影响
由图99和图100可以看出,胞核中润滑元素组分及其含量极大地影响了其变形量及润滑膜厚度。
(1)对于Pb 胞核最大变形量和润滑膜厚度随Pb在胞核中的体积含量的上升而增加,这是由于Pb在胞核各组成成分中具有最大的线膨胀率,随着Pb在胞核中比例逐渐增加,胞核线膨胀率逐渐增加,从而润滑膜厚度也会相应地增加。
(2)对于Sn 元素Sn的线膨胀率仅次于Pb的线膨胀率,因此随着Sn在胞核中比例的逐渐增加,有利于润滑膜厚度的增加。
(3)对于Cu 胞核的最大变形量和润滑膜厚度随着Cu在胞核中的体积含量上升而减小,这是由于Cu在胞核各组成中具有最小的线膨胀率。随着Cu在胞核中比例的逐渐增加,胞核的线膨胀率逐渐降低,使得胞核的最大变形量下降,润滑膜厚度也相应地变薄。
(4)对于Ag 由于Ag在胞核各相中的线膨胀率较低,仅高于Cu的线膨胀率,因此随着Ag在胞核成分逐渐增加,胞核的最大变形量会相应减少。
显然,就润滑体最大变形量而言,有限元分析与理论分析所揭示的润滑元素对胞核心变形的变化规律是相吻合的。
5.5.3 胞壁组分及含量对胞核变形量(润滑体析出)的影响
为了研究胞壁中各组分的体积含量对胞核变形(润滑体析出)的影响,分别研究了硬质相组分Fe,Cr,W,Mo,V和TiC在胞壁中不同体积含量下的胞核最大变形量。其中,胞壁的物理性能和机械性能随组分体积含量变化值可按表达式(146)计算(计算时,胞核中Pb-Sn-Cu-Ag元素按质量比3∶20∶47∶30配比);而润滑膜厚度通过式(154)计算,胞壁(基体)中各组成成分对胞核最大变形量之影响规律见图101,而润滑膜厚度则通过式(154)计算,其结果见图102。
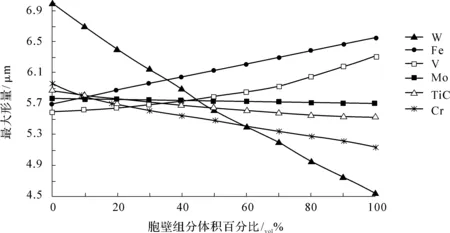
图101 胞壁组分及含量对胞核最大变形量的影响

图102 胞壁组分及含量对润滑膜厚度的影响
由图101和图102可以看出以下几点。
(1)对于Fe 胞核的最大变形量和润滑膜厚度随着Fe在基体中的体积含量的上升而增加,这是由于Fe在基体各组成成分中具有最大的线膨胀率,随着Fe在基体中比例的逐渐增加,基体的线膨胀率逐渐增加,因此,胞核的最大变形量会增加,从而润滑膜厚度也会相应地增加。
(2)对于Cr 由于Cr在胞壁各相中的线膨胀率较低(4.9×10-6K-1),与基体硬质相中具有最低的线膨胀率的W(4.5×10-6K-1)相近,因此随着Cr在胞壁成分逐渐增加,胞核的最大变形量会相应减少,从而润滑膜厚度也相应地减少。
(3)对于W和Mo 由于W和Mo在胞壁各相中的线膨胀率最低,因此其分析结果和Cr相似,即胞核的最大变形量随W和Mo的成分的体积含量增加而减少。
(4)对于V 由于V在基体各相中的线膨胀率较高,仅次于Fe的线膨胀率,因此随着V在基体成分逐渐增加,相同温升条件下,胞核的最大变形量会相应增加。
(5)对于TiC TiC在基体各相中的线膨胀率较Fe和V低,随着TiC在基体成分逐渐增加,胞核的最大变形量会相应减少。
6 高温发汗自润滑机理及其润滑控制设计
6.1 高温发汗自润滑机理
6.1.1 试验设备与条件
6.1.1.1 试验设备
摩擦学试验在XP-5销-盘数控高温摩擦磨损试验机上进行,其工作原理见图103。试验机的主要技术参数如下,试验载荷为0~1 000 N,试验温度为室温~1 200 ℃,试验转速为300~2 000 r·min-1。

1主轴;2加热元件;3电炉;4销试样;5摩擦盘;6试样托盘;7压力传感器;8摩擦力传感器;9炉体;10试验气氛
销试样4安装在与主轴1相连接的夹具上,摩擦盘5安装在试样托盘6上。试验时,销试样4与摩擦盘5之间的接触通过砝码加载;压力传感器7和摩擦力传感器8及相应的数据采集系统将自动测量和记录摩擦过程中的载荷和摩擦因数。环境温度控制由装有热电装置系统的电炉3中的加热元件2实现;炉内通入试验气氛10改变工作环境气氛;试验速度由调速系统通过电机控制主轴1实现无级调速。在试验过程中,载荷分布通过压力传感器7,摩擦力通过摩擦力传感器8实现实时测量,并通过计算机自动计算和纪录摩擦因数和载荷值,试验过程中的温度、转速、载荷、摩擦力及摩擦因数等试验曲线可同步显示。
6.1.1.2 试验试样
销试样为高温发汗自润滑材料(HTSSLC),参与摩擦的接触面为球冠端面(见图104a),粗糙度Ra为0.20~0.80 μm。

图104 销试样及磨损尺寸
摩擦盘为φ55 mm×8 mm的2Cr13金属盘或Al2O3陶瓷盘。2Cr13金属盘试样在热处理后的硬度HRC为40~45,粗糙度Ra为0.32 μm;在2Cr13金属盘表层喷涂的Ti-Al陶瓷涂层,硬度HRC为62~67,表面粗糙度Ra为0.20 μm。Al2O3陶瓷盘硬度HRC为67~70,粗糙度Ra为0.32 μm。
每次试验前,试样均应依次在蒸馏水及丙酮中超声波清洗5 min,烘干待用。
6.1.1.3 试验及测试
试验过程中,摩擦因数可通过试验机处理程序界面直接读取,磨损率则通过下式计算。
(155)
式中,K为磨损率,mm3·(N·m)-1;Vw为磨损体积;Dp为销试样相对于盘试样回转直径,m;nr为主轴转速,r·min-1;t0为摩擦磨损试验时间,min;P为试验载荷,N;Δw为磨损前后质量损失,g;ρ为盘试样的密度,g·cm-3。
磨损体积可在磨损前后通过光学显微镜测量销试样端部直径(见图104(b))后计算得到[72]。

(156)
式中,Vw为磨损体积;d1为销试样在磨损前的销球端面直径;d2为销试样在磨损后的销球端面直径;ro为销球半径。
在材料摩擦磨损试验后,用扫描电镜(SEM)分析试样试验后摩擦表面形貌特征及变化。能谱分析仪(EDS)进一步对摩擦表面成分及组成元素进行微观分析;盘表面润滑膜厚度通过表面轮廓仪测量。
6.1.2 HTSSLC的摩擦学特性研究
鉴于HTSSLC的胞体结构特征,可通过改变胞核材料性能降低其材料界面剪切力,或改变其基体组分提高其胞壁高温屈服强度,以实现高温减摩和改善材料磨损性能的效果,计算模型如下。
f=τ/σs
(157)
式中,f为摩擦因数;τ为材料界面剪切力;σs为材料屈服强度。
本研究以烧结高速钢陶瓷为基体,通过被熔浸材料组分设计,以降低其胞核润滑体剪切强度和增强扩散活性,改善其摩擦学性能。
图105为具有GLPS的烧结高速钢陶瓷基体(曲线A),以及在GLPS中分别熔浸Ag(曲线B)和Pb(曲线C)形成的复合材料,在800 ℃工况下的摩擦过程曲线。
由图105可以看出,每组曲线的摩擦因数都呈现出在摩擦进行40 min后随时间增加而降低的趋势,其中熔浸了Ag(曲线B)或Pb(曲线C)形成的复合材料,其摩擦因数降幅较大,且在60 min后都趋向平稳。在稳定阶段,熔浸了Ag或Pb所形成的HTSSLC,其摩擦因数仅为基体的35%~40%;且熔浸了Pb所形成的HTSSLC,其摩擦因数比熔浸了Ag所形成的HTSSLC要低,其原因是Pb的熔点比Ag低,且在430~850 ℃,Pb易被氧化,生成PbO。PbO具有良好的高温润滑性[39]。显然,熔浸元素的熔点及其高温性能是影响HTSSLC摩擦因数的重要因素。

图105 高速钢陶瓷基HTSSLC的摩擦过程曲线(试验载荷P=50 N(12 MPa),摩擦盘匹配副Al2O3)
图106(a)和图106(b)分别为曲线A和曲线B在磨损试验后的表面形貌。由图106可以看出,高速钢陶瓷基体表面呈现明显的粘着现象,而熔浸了Ag所形成的HTSSLC,其磨损表面呈现明显的熔融膜特征。

图106 磨损表面形貌(试验条件与图105相同)
为了获得理想的复合润滑体,通过大量的润滑组分设计,在润湿性、析出量和成膜特性研究基础上,选择出数种复合润滑体进行摩擦学试验。
图107为熔浸复合组分润滑体形成的HTSSLC的摩擦因数曲线,曲线A,曲线B,曲线C和曲线D所对应的复合润滑体组分分别为47Pb28Sn19Ag6Cu,50Pb30Sn20Ag,50Pb20Sn20Ag10Sb和52Pb13Au20Cu15Sn。

图107 熔渗不同组分复合润滑体的HTSSLC的摩擦因数
由图107可以看出,与其他润滑体组分相比,熔渗47Pb28Sn19Ag6Cu所形成的HTSSLC的润滑性能最好,摩擦因数下降到0.3以下,且从摩擦行程开始,其摩擦因数就呈现出低值(见图107中曲线A)。究其原因,是因为复合润滑体与基体的润湿性和互溶性较好,制备的润滑层深度较大,摩擦过程中析出了足够多的润滑体,使摩擦表面能形成完整的润滑膜。与此同时,由高润湿性和互溶性润滑体形成的表面膜也具有与基体结合强度高的性能,使其在摩擦过程中不易破裂而稳定了其摩擦过程。
为了研究HTSSLC润滑过程中的润滑膜现象,取在基体微孔胞体结构中熔浸了47Pb28Sn19Ag6Cu形成的HTSSLC进行摩擦过程试验(见图108)。

图108 高温发汗材料摩擦过程曲线(配副Al2O3,载荷P=50 N,速度V=0.1 m/s,温度T=600 ℃)
显然,图108中的曲线,其变化趋势与图105相似,但由于在润滑体设计时考虑了复合效应,因而,摩擦因数更低、摩擦过程更稳定,这表现在:在摩擦初期,摩擦因数由0.2左右迅速上升到0.3以上,随后逐渐下降,并稳定于0.21附近。
图109为图108的试验过程的微观分析与膜厚测试数据。图109(a)为磨损后的销试样表面形貌,图109(b)为试验后Al2O3陶瓷盘的转移膜成分。

图109 摩擦表面转移润滑膜及其厚度
由图109可以看出,转移膜成分中除了含有Fe和W等基体成分及摩擦盘的试样元素Al外,还含有丰富的Pb,Ag,Cu和Sn。显然,熔浸在基体中的润滑体在摩擦过程中从基体微孔中析出,并富集于摩擦表面,形成了润滑膜的组元。图109(c)为磨损试验后Al2O3陶瓷盘的宏观表面膜现象,反映出其表面膜的完整性(其膜组分的EDXA分析图谱见图109(b))。图109(d)为该表面膜在A-B截面(见图109(e))上的表面膜厚度测量结果。可以看出,与无转移膜形成的两端相比,在轨迹中部有转移膜形成区域,其形貌高度高出约20 μm。
由以上试验结果可知,HTSSLC的润滑过程,能在摩擦界面上形成完整的润滑膜,其润滑性能取决于被熔浸润滑体的组元设计。
6.1.3 润滑膜成膜条件及其润滑机理
基于胞核润滑元素析出理论,当HTSSLC胞核中复合润滑体的热膨胀系数大于材料基体的热膨胀系数时,在高温状态下,其润滑体将沿微孔析出并富集在摩擦表面。图110(a)为HTSSLC加热到600 ℃时,润滑体元素在其表面呈汗珠形态分布情况;图110(b)为该析出物的组分分析,其主要成分为Pb,Ag和Cu,这证实了胞核润滑元素析出理论的正确性。

图110 HTSSLC加热后的表面析出物形态
图111(a)给出了熔浸Ag后的HTSSLC在高温工况下(试验温度600 ℃;载荷90 MPa;滑动速度0.139 m·s-1;磨损时间120 min)的磨损表面SEM形貌,图111(b)为图111(a)表面的元素分布。

图111 熔浸Ag的HTSSLC在高温摩擦后的表面形态
比较图111(a)和图111(b),可以看出,在严重擦伤部位,由于高温-摩擦热-应力的联合作用,Ag扩散并富集在严重擦伤部位。显然,严重擦伤部位的摩擦阻力大,引起的微接触区摩擦热也增高,增大了基体中润滑元素沿有序微孔通道扩散(或泄出)的驱动力,从而诱发了高摩擦阻力(或擦伤)区的润滑元素富集现象(图111(a)为润滑元素Ag在严重擦伤部位富集情况),实现了高温动态择优自润滑。这表明,HTSSLC解决了极端高温重载工况下的高温自润滑问题。
图112(a)为图105中的曲线B在试验完成后的磨损表面膜形态,图112(b)为Ag的分布。图112的典型特征是,从微孔中析出的Ag在摩擦表面形成了一层膜,且微孔周围的Ag明显地高于其它部位。这种现象一方面反映出在高温发汗润滑过程中的高温熔融与摩擦力对润滑膜成膜的影响,另一方面也反映出胞核中的润滑体从微孔中析出及其扩散过程。

图112 熔浸Ag的HTSSLC磨损表面膜及其Ag分布
6.1.4 工况参数及润滑组分对高温发汗润滑的交互影响
基于胞核润滑元素析出理论,HTSSLC中的润滑体析出不仅与润滑体组分、微孔结构参数及基体特性有关,而且还与工况参量有关。
图113为GLPS的基体为高速钢基陶瓷,在微孔中分别熔浸不同组分的Pb-Sn-Ag-Re复合润滑体时,从室温~800 ℃进行摩擦磨损试验的摩擦因数曲线。
由图113可以看出,摩擦因数在试验温度为300 ℃时下降明显,此后趋向于稳定;且Pb-Sn含量越高,摩擦因数越低稳定性也越好。

图113 熔浸Pb-Sn-Ag-Re复合润滑体后的HTSSLC摩擦因数随温度变化曲线
图114为图113相对应的磨损曲线。

图114 熔浸Pb-Sn-Ag-Re复合润滑体后的HTSSLC磨损率随温度变化曲线
由图114可以看出,在300 ℃后,磨损率则随温度的升高而升高,且磨损率较高的不是Pb-Sn含量最高的元素组,而是15%Pb-Sn-10-0.7Re元素组。
上述的试验结果表明,在HTSSLC中,润滑体组分对材料摩擦磨损性能的改善是明显的,且其摩擦因数能维持在较宽的温度范围。润滑体组分及合金温度对磨损也有影响,但其变化幅度不太大,如能设计其润滑体组分含量,则可消除这种影响,并使得材料在宽广的温度范围内具有良好的摩擦和磨损性能。
图115给出了GLPS的金属陶瓷烧结基体(曲线A)、熔浸Pb-Sn-0.3Re(曲线B)及Pb-Sn-10Ag-0.3Re(曲线C)复合润滑体的HTSSLC,在不同载荷下与Ti-Al陶瓷涂层配对(试验温度600 ℃,滑动速度0.139 m·s-1)时的摩擦因数与载荷间的关系曲线。
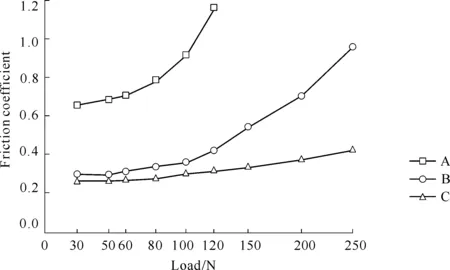
图115 GLPS金属陶瓷基体及熔浸了Pb-Sn-Ag-Re的HTSSLC摩擦因数随载荷变化趋势
由图115可以看出,与基体相比,在较宽广的载荷范围内,熔浸了复合润滑体Pb-Sn-0.3Re或Pb-Sn-10Ag-0.3Re的HTSSLC,其摩擦因数都较低;但在试验载荷达到90 N后,随着试验载荷持续增加,熔浸Pb-Sn-0.3Re的HTSSLC的摩擦因数急剧升高;而熔浸Pb-Sn-10Ag-0.3Re的HTSSLC的摩擦因数虽然也有所升高,但其上升幅度远比熔浸Pb-Sn-0.3Re的HTSSLC的摩擦因数要小。显然,这与膜的承载能力有关。
为了进一步探讨高温发汗润滑过程中软金属熔融膜的承载能力,以Pb为润滑体填充到中,在800 ℃温度下进行载荷比较试验。图116分别为载荷50 N和100 N时的摩擦过程曲线。比较曲线A和曲线B,可以看出,熔融膜的形成时间为40 min左右。熔融膜形成后的摩擦因数取决于载荷,由于熔融膜具有液态特征,液态膜的承载能力有限,只有当外载荷低于膜的承载能力时,这种液态减摩效果才比较显著,而在重载情况下,液态膜仍以边界膜形态呈现。

图116 熔浸Pb的HTSSLC在800 ℃下的摩擦因数随时间变化趋势
图117为图116中曲线A磨损后的表面磨损表面SEM形貌及其Pb分布。比较图117(a)和图117(b),可以看出,Pb富集于表面严重擦伤之部位,这与图112所显示的润滑机理完全一致,仅仅是由于Pb的熔点及扩散系数与Ag有异而导致的分布形态差别。

图117 熔浸Pb的HTSSLC在高温摩擦后表面形态
上述研究表明,工况参数及润滑组分对HTSSLC的交互影响主要体现在润滑膜的工况适应性及减摩性能方面,并不影响润滑体的析出机理及其在摩擦表面富集过程。因此不影响材料实现高温动态择优自补偿润滑功能,但通过润滑体的组分优化设计将可进一步改善其润滑特性,这将是HTSSLC能够解决极端高温重载工况下的高温自润滑问题的重要内容。
6.2 高温发汗自润滑控制设计
高温发汗自润滑过程是润滑体在摩擦热-应力作用下从基体孔隙中析出,并在摩擦表面富集及润滑膜形成与破坏的动态过程,该过程决定了其润滑性能。由于该过程是在高温下进行的,同时受到摩擦表面形貌、表面接触应力、温度场等因素的影响,难以实现其过程的动态观察和测量。基于润滑元素析出、润滑膜生成与破裂的随机特点和离散特性,本研究团队采用元胞自动机(automata)模拟仿真其动态过程,进而实现高温发汗自润滑控制设计(design of lubricating control)。
6.2.1 高温发汗自润滑动态演化过程
元胞自动机是定义在一个具有离散、有限状态元胞组成的空间上,并按照一定局部规则,在离散的时间长度上演化的动力学系统[73]。基于元胞自动机处理离散及复杂系统时空演化过程的独特优势,建立HTSSLC的摩擦表面动态演化模型(Dynamic Evolution Model of the Worn Surface,DEMWS),研究高温发汗自润滑过程及其动摩擦因数(dynamic friction coefficient)、摩擦表面形貌(morphology of the worn surface)及润滑体分布状态(distribution of solid lubricants)。
在高温摩擦过程中,润滑体由材料微孔中析出,在摩擦表面呈颗粒微元状,并在摩擦力作用下通过拖敷和挤压形成润滑膜。流动过程中部分润滑微元粒子在磨损严重的低凹区域形成富集,其过程可归纳为“润滑体析出→微元粒子流动→润滑膜形成→润滑膜破坏”的动态循环过程(见图118)。

图118 HTSSLC表面膜形成与失效机理
为了发挥HTSSLC的高温自润滑功能,在工程中,通常是在环境温度上升到给定的工作温度时才驱动轴承。
在加热过程中,基体中的润滑体已析出到摩擦表面(见图118(a)),在摩擦初始阶段,由于摩擦表面还没有形成润滑膜,相互接触的微凸体间由于高摩擦因数而产生摩擦热-应力,这促使更多润滑体从接触区微孔中析出,同时在接触区也将有微凸体发生磨损有形成磨损粒子,磨损粒子与润滑体一同在对偶摩擦副的切向力作用下铺开到摩擦表面(为方便讨论,将润滑体与磨损粒子统称为润滑粒子体(lubricating particle))。
部分润滑粒子体在流动过程中富集在局部区域,在对偶面的拖敷及挤压作用下形成润滑膜(见图118(b)),其余部分润滑粒子体则在离开摩擦表面形成实质上的磨损粒子,但此时已形成润滑膜的区域摩擦因数降低,摩擦热-应力也降低,表面润滑元素浓度达到平衡,润滑元素不再从微孔中析出,表面磨损可忽略不计。
经过一段时间后,该区域相对于其他微凸体又显凸出,而又导致其摩擦热-应力上升,增加了润滑膜的破裂倾向,直至润滑膜破裂(见图118(c)),并转化为润滑粒子体流走(见图118(d)),导致摩擦系统中的润滑粒子体密度上升→富集→生成润滑膜→润滑膜破裂。
如此循环的本质是摩擦副在一定的外加载荷下,形成“摩擦生热→应力产生→润滑体析出→润滑膜形成→润滑膜破裂→磨损粒子形成→表面形貌改变”等相互作用和耦合的动态平衡系统,其相互关系见图119。在该动态平衡系统中,当外加载荷发生改变时,引起系统内润滑膜、磨损、摩擦热及表面形貌等因素发生改变,进而影响各因素之间的相互关系,使系统处于新的平衡状态。

图119 摩擦系统影响因素关系分析
本研究团队基于这种系统再平衡规律建立元胞自动机模型,可实现高温发汗自润滑动态过程的演算。
6.2.2 动态演变过程计算的基础表征模型
6.2.2.1 计算时的粗糙表面表征模型
粗糙表面形貌的表征方法通常有正向建模(forward modeling)和逆向建模(reverse modeling)等两种。逆向建模是指应用三维数字化测量仪等表面形貌测试仪器测量实际粗糙表面轮廓坐标值,然后基于测量值构建数字表面模型。正向建模是指采用数学方法产生虚拟表面。
基于高温发汗自润滑过程的不可测量性,本研究团队采用正向建模以连续不可微分且具有自仿射分形特征的W-M分形函数产生原始摩擦粗糙表面[74]。
(158)
式中,z(x,y)为表面上平面直角坐标为(x,y)处的高度;Lo为取样长度;Gh为高度比例参数(分形粗糙度);D为表面的分形维数,2
6.2.2.2 计算时表面接触状态表征模型
设摩擦表面任一微凸体i,若其相对于基准水平面高度为z,受压缩后产生的变形量为Δhi,则在摩擦过程中,粗糙表面的接触是一个混合的弹塑性系统。根据弹塑性接触理论,可针对弹性变形、弹塑性变形和完全塑性变形等情况,建立以下形式的表面接触状态表征模型[32]。
(1) 当发生弹性变形(elastic deformation)时,发生接触的微凸体产生的接触应力
(159)

Ai=πΔhiRz
(160)
式中,Ai为微凸体接触面积。
(2) 当发生弹塑性变形(elastic-plasticity deformation)时,发生接触的微凸体上产生的接触应力
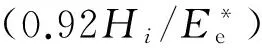
(161)
Δh02=54Δh01
式中,Hi为较软微凸体材料的硬度,其大小受温度的影响;Δhi为微凸体开始发生弹塑性变形时对应的变形量。
微凸体的接触面积
(162)
(3) 当发生完全塑性变形(plastic deformation)时,发生接触的微凸体上产生的接触应力
pi=Hi
(163)
微凸体的接触面积
Ai=2πΔhiRz
(164)
在摩擦过程,其随摩擦表面形貌发生改变而改变。因此,平均曲率半径是关于时间的变量。对于已知粗糙表面,平均曲率半径可以通过下面方法计算[75]。
设取样长度为Lh,在以长度为LS的离散间隔中抽查微凸体高度zi。如果zi-1,zi和zi+1为相邻的3个微凸体高度,则微凸体i处的曲率
(165)
式中,κi为微凸体i处的曲率。
在取样平面内,微凸体均方根曲率平方
(166)
式中,nz为微凸体样本数目;σκ为取样平面均方根曲率。
(167)
所有微凸体上法向载荷pi之和应与总法向载荷P相等,即
(168)
6.2.2.3 计算时的摩擦力表征模型
设摩擦因数为f,摩擦力为F,法向载荷为P,由经典摩擦理论[76],可得
F=fP
(169)
基于高温发汗自润滑机理,在摩擦过程中,接触表面微凸体的润滑膜覆率是随机的,即润滑膜对微凸体的覆盖存在完全覆盖(full covering)、部分覆盖(partial covering)和表面膜未形成(no covering)等3种情况。此时,在摩擦系统内的摩擦力表现形式
(170)
式中,nz为微凸体数目;fi为微凸体i上的摩擦因数。
由于所有微凸体上法向载荷之和与摩擦面上总的载荷相等,即
(171)
则摩擦表面整体摩擦因数
(172)
6.2.2.4 计算时的摩擦温度场表征模型
在高温摩擦环境中,摩擦热与环境温度耦合导致接触区温度上升,加剧微凸体磨损,同时导致局部润滑体析出速度及润滑状态发生改变。若把每一个接触微凸体i看作一个点热源,在时间上离散后,其滑动速度vt的时间间隔Δt内产生的摩擦热
Qi=fipiAivtΔt
(173)
则,HTSSLC的传入热量
Qi1=ζ1ρ2c2Qi/(ζ1ρ2c2+ζ2ρ1c1)
(174)
式中,ζ1和ζ2为两种材料的导热系数;ρ1和ρ2为两种材料的密度;c1和c2为两种材料的热容量;下标1和下标2为HTSSLC与对偶材料的摩擦面。
根据热传导理论,半空间无限体上点热源在某一时刻,发出热量Qi1全部传入半空间无限体内,通过在时间间隔Δt后在相对位置(x,y,z)处引起的温升[77],即可计算摩擦表面的温度分布。
(175)
式中,α为材料散热系数。
在Mx×Ny个单元的模型空间,从0~to时间长度分为Nt个时步Δt,式(175)在空间和时间尺度上求和,在k时步,模型网格单元(i,j)温升离散表达形式
(176)
式中,Ci,j,k为温升影响系数。
(177)
式中,(xij,yij,zij)为计算温升位置相对于点热源的坐标。
6.2.2.5 计算时的表面磨损模型
基于高温磨损过程是以塑性变形进而产生粘着的磨损形态,可将Archard计算模型[76]应用在元胞自动机的微凸体磨损中,则在时间间隔Δt内微凸体在其高度方向的磨损
(178)
式中,Ki为接触区磨损率;pi为接触应力;Ls为滑动距离,在模型中为单元的尺度;Hi为接触区局部硬度。
在高温摩擦时,由于摩擦表面温度分布不均,其局部硬度和磨损率都不是常数。研究发现高温模具材料磨损量与局部硬度、磨损率及温度的函数有如下关系[78]。
(179)
式中,T为温度。
在模型中,微凸体的磨损以产生的磨损粒子来表示,每个磨损粒子代表一定的微凸体厚度,由式(178)所得的磨损量在模型中换算为产生磨损粒子的几率。
6.3 高温发汗自润滑动态演化模型
6.3.1高温发汗自润滑动态演化模型及其离散化
为了表征摩擦表面形貌高度在摩擦过程中的演化,本研究采取在二维模型基础上对每一个元胞引入一个高度变量来实现,使其计算时可直接输入测量或模拟产生的摩擦表面高度变量数据。
高温发汗自润滑的摩擦表面主要由硬质基体及其在硬质基体孔隙中嵌入软质润滑体等两相结构组成。对于硬质基体构成的微凸体,在摩擦过程中可分为无润滑膜或覆有润滑膜等两种情况。
当与有润滑膜覆盖的微凸体发生接触时,由于有润滑膜保护,磨损可以忽略不计;当与无润滑膜的微凸体发生接触时,由于无润滑膜保护,接触面摩擦因数大,且往往会发生粘着磨损。因此,模型中的元胞可分为润滑体元胞(lubricant cell)(见图120(a)之1)、基体元胞(matrix cell)(见图120(a)之2)和润滑膜元胞(lubricating cell)(见图120(a)之3)等3种类型,其中,基体元胞和润滑膜元胞等两种元胞间可以互相转化。图120(b)为部分元胞自动机模型,图中白色网格代表基体元胞,灰色网格代表润滑膜元胞,黑色网格代表润滑体元胞。

图120 高温发汗润滑动态演化模型
【假设11】 基体微孔中润滑层在不同深度上的孔隙度不变,则在给定的时间长度内,材料的磨损厚度相对于孔隙深度较小,使润滑体元胞的位置状态保持不变。
取HTSSLC之中1 mm×1 mm的摩擦面积为研究对象,其表面形貌按式(156)生成。对其进行离散化,并建立相应的元胞网格。
由于HTSSLC基体中微孔直径主要分布范围为10~20 μm[22],取包含100×100个元胞(每个元胞的大小为10×10 μm2)的整个模型。
6.3.2 摩擦表面润滑过程演化规则
6.3.2.1 润滑粒子运动规则
高温发汗自润滑性能取决于摩擦表面润滑膜的生成及分布。润滑膜的形成和破坏与润滑粒子、摩擦表面温度及接触应力分布有关。在模型中,润滑膜由一定数目的润滑粒子转化而成,由于润滑膜和润滑粒子都代表一定量的润滑体,润滑膜的生成与破坏、磨损粒子的产生都会引起元胞高度的变化,计算时通过元胞高度增加或减去润滑膜厚度(或润滑粒子厚度)来表示。
润滑膜厚度(thickness of the lubricating film)(或润滑粒子厚度)是指润滑膜(或润滑粒子)代表的润滑体平铺在元胞上的厚度。
摩擦表面上润滑体粒子体分布(distribution of lubricating particles)用润滑体粒子密度(density of lubricating particles)表示。某时刻某一元胞上的润滑粒子密度指此时该元胞上润滑粒子体数目。
(1)润滑粒子的产生HTSSLC进入高温环境工作时,环境温度发生改变,基体微孔(即润滑体元胞)中的一部分固体润滑体粒子在温度应力作用下析出摩擦表面,为初始润滑状态的建立创造了条件。在摩擦过程中,发生接触的元胞摩擦产生热量,使附近元胞温度上升,促使附近微孔(润滑体元胞)中的润滑体粒子析出摩擦表面。发生接触的基体元胞磨损产生磨损粒子,元胞高度减去产生的磨损粒子厚度,该元胞上润滑粒子密度加上产生的磨损粒子数目。
(2)润滑粒子的流动在摩擦过程中,润滑粒子随着对偶摩擦件一起流动。粒子的流动过程取决于受载后摩擦表面高度轮廓的分布状态。在图121中,元胞1中的润滑粒子在下一时刻移动到下一邻居元胞(2,3,4)的条件是元胞1的高度加上润滑粒子厚度大于目标元胞的高度值。如果条件满足,该粒子以一定几率向下一元胞移动。

图121 润滑粒子的移动
6.3.2.2 摩擦表面润滑膜演化规则
在进行元胞状态计算时元胞的邻居采用冯·诺依曼邻居(Von Neumann Neighborhood),即中心元胞上下左右4个元胞为其邻居。在某一时刻,若某一基体元胞处的润滑粒子密度足够大,同时该元胞发生接触产生接触应力,则该元胞上的润滑粒子以一定几率转化为润滑膜,该元胞由基体元胞转变为润滑膜元胞,润滑粒子密度减去转化为润滑膜的润滑粒子数,元胞高度加上润滑膜厚度。
如果某一时刻某元胞为润滑膜元胞,则该元胞以一定几率发生破裂,转化为基体元胞。元胞高度减去润滑膜厚度,同时产生相应数目的润滑粒子。转化几率受该元胞此时接触应力及元胞温度大小的影响。
润滑膜元胞生成的几率受其邻居元胞状态的影响,邻居元胞为润滑膜元胞的数目越多,其几率越大。润滑膜元胞产生破坏的几率与其邻居上一时步润滑膜元胞是否产生破坏有关,若有状态为润滑膜的邻居元胞发生破坏,该中心元胞产生破坏的几率增大,产生破坏的元胞越多,几率越大。
6.3.2.3 摩擦表面受力及形貌演化规则
摩擦表面磨损涉及摩擦表面形貌、外加载荷、元胞状态、接触应力和摩擦热(用温度表示)等因素之间的关系。
从某一时刻的表面形貌开始(见图122(a)),在对偶平面所加载荷P作用下计算各个元胞发生的变形量Δhi。根据粗糙表面弹塑性接触理论,由各个元胞产生的变形量,计算出相应的接触应力分布及在载荷作用下的新的表面形貌高度轮廓分布。应当指出的是,由于润滑体元胞中的润滑体在高温下硬度很小,甚至处于熔融状态,因此,并不是所有与对偶摩擦面发生接触并产生变形的元胞都具有接触应力,部分润滑元胞上的支撑力为零(见图122(a)中润滑体元胞17);此时,润滑膜元胞上的接触应力主要靠润滑膜下基体承担,计算时可忽略其对接触力的影响。所有接触元胞上产生的支撑力总和与外加载荷P相等,这一过程通过迭代计算来完成。
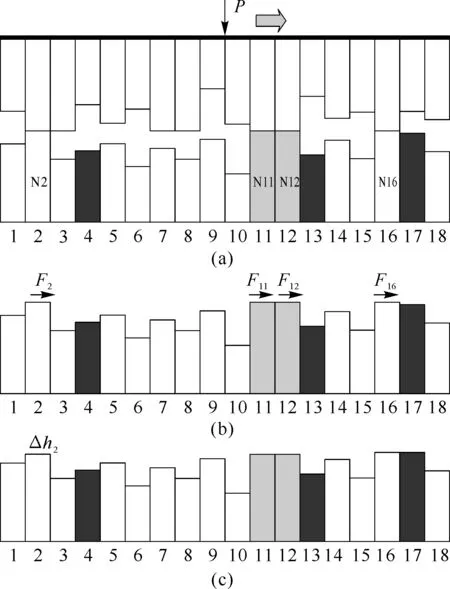
图122 摩擦表面形态演变模型
由计算得到的接触应力分布及此时的元胞分布状态计算在相应元胞上产生的摩擦力Fi及热量见图122(b)。由每个元胞产生的热量根据传热学原理计算得出各个元胞上的温升,在模型时间和空间上进行叠加,得到整个元胞自动机模型所有元胞上的温度分布。在摩擦过程中,润滑膜元胞由于摩擦因数远小于基体元胞,所以产生的热量很小。润滑体元胞上接触应力为零,不产生热量,在热传导过程中吸收邻居元胞传递的热量使其温度发生改变。
由以上两个时步得到的接触应力分布及温度场分布,可计算接触基体元胞上产生磨损粒子的概率,继而得出相应接触基体元胞上产生的磨损粒子数。由于每个磨损粒子代表一定的元胞厚度,在对应的元胞上减去相应磨损粒子厚度得到新的表面高度轮廓,作为下一时步的输入。由于接触元胞是以一定几率产生磨损粒子,所以并不是所有的接触基体元胞都会有磨损粒子产生(例如,图122(c)中元胞16没有磨损粒子产生,高度不变,而元胞2有磨损粒子产生,元胞高度减去磨损粒子高度形成新的元胞高度)。这样做便于把磨损量与产生的磨损粒子联系起来,同时还有利于与宏观磨损试验数据相比较,这种处理方法与粘着磨损理论(adhesion wear theory)相符合。
由于受润滑膜保护的元胞不发生磨损,经过一段时间后,其高度将比其他元胞高些,成为新的凸峰,开始新的计算循环(计算流程见图123)。

图123 计算模型流程
6.4 HTSSLC的摩擦动态演变过程分析
为了利用所建模型对HTSSLC的摩擦动态演化过程进行仿真分析,选择计算参数如下:销试样HTSSLC基体,其孔隙度为0.15,微孔中分别熔浸Ag或Pb作为润滑体;盘试样为Al2O3陶瓷,模型中载荷为12 MPa,滑动速度为0.1 m·s-1;计算时,销试样和盘试样的材料属性见表31。

表31 模型计算采用的材料属性
6.4.1 接触应力、温度场及磨损率仿真分析
在摩擦过程中,HTSSLC摩擦表面上的载荷及耐磨性主要由基体承担。同时,由于润滑体材质较软,摩擦表面的形貌主要取决于基体微凸体高度的演化。图124为在不同载荷下摩擦表面应力与温度场分布情况。
图124 载荷对摩擦表面应力及温度场的影响
由图124可见,在载荷较小时,摩擦表面上发生接触的微凸体较少,接触应力也较小,此时温度场幅值较小(见图124(a)和图124(b))。随着载荷增大,发生接触的微凸体增多,接触应力增大,有更多的微凸体发生塑性变形甚至粘着而造成摩擦热增加,摩擦温度场的幅值也增大(见图124(c)和图124(d))。
图125为在不同时步(time step)(1~400time step,401~800time step和801~1 200time step)内,摩擦系统在不同载荷下所产生的以磨损粒子数表征的磨损量。

图125 载荷对磨损的影响
从图125可以看出,磨损量随载荷的增加而增大。显然,这种磨损随载荷变化的规律可反映出Archard计算模型及工程磨损试验的变化趋势。
6.4.2 动态摩擦过程曲线仿真分析
图126(a)和图126(b)为HTSSLC摩擦因数的仿真模拟曲线及其摩擦试验曲线。对比图126(a)和图126(b),可以看出,两者的变化趋势非常相近,且都反映了其摩擦过程,在摩擦阶段刚开始时摩擦因数较大,波动也较剧烈(这是由于在初始阶段接触面积较小,接触处接触应力较大,局部微凸体粘着,润滑膜容易破裂,因而导致摩擦因数较大);在经过一段时间后,摩擦因数逐渐减小并且趋向稳定。

图126 HTSSLC摩擦因数仿真模拟及试验摩擦因数变化曲线
6.4.3 表面形貌及润滑体分布
图127(a)和图127(b)为HTSSLC的摩擦表面形貌轮廓及摩擦表面润滑体分布的模拟仿真结果,图127(c)为在800 ℃高温摩擦试验后的磨损表面润滑体的分布情况,

图127 模拟及试验摩擦表面的润滑体分布
由图127(a)可以看出,经过一段时间摩擦后,从HTSSLC内部析出的润滑体在摩擦表面发生磨损的区域形成了连续的润滑膜。由图127(b)可以看出,在摩擦表面局部凹陷区域,出现了润滑体富积现象。
比较图127(b)和图127(c),可以看出,模拟计算结果与摩擦试验后的表面润滑体的分布情况完全符合。这表明,该元胞自动机模型可有效地用于分析HTSSLC的动态摩擦过程,预测组分设计或工况条件对其润滑性能的影响,以指导其材料制备与寿命预测。
6.5 高温发汗自润滑控制机理研究
6.5.1 高温发汗自润滑状态演化机理
HTSSLC的摩擦学特性主要取决于两个方面,一是润滑层的组分及基体微孔结构形态,在给定的多孔金属陶瓷基体条件下,其摩擦学特性主要取决于复合润滑体的组分及其在润滑层孔隙中的分布;二是在摩擦过程中,复合润滑体向摩擦表面的析出量及其在摩擦表面的流动及润滑膜的形成与破坏过程,这一过程与摩擦工况密切相关。显然,仿真模拟高温摩擦动态过程,可揭示其润滑机理,进而通过润滑体组分或摩擦工况设计实现其润滑控制。
由于在高温摩擦过程中,基体微孔中的润滑体是在摩擦热-应力作用下沿有序孔向摩擦表面析出,因此,表面润滑膜的形成与润滑体元素扩散率及摩擦表面粗糙度有关[10]。图128为HTSSLC润滑状态演化模型。
在预热阶段,由于微孔中的润滑体未析出到摩擦表面,因而摩擦副处于干摩擦状态(见图128(a))。随着环境温度升高或摩擦热作用,润滑体在热应力作用下析出到摩擦表面,分布在粗糙表面的凹谷中,当析出的润滑体不足以隔离摩擦表面时,润滑体只在摩擦面部分区域形成边界润滑膜(见图128(b)),从而使摩擦副处于边界润滑状态。当温度进一步升高使析出润滑体足够量时,在摩擦表面形成完整的润滑膜,产生摩擦的表面间被完全隔离,摩擦副处于全膜润滑状态(见图128(c))。因此,HTSSLC的摩擦学性能取决于摩擦表面润滑膜的覆盖情况,润滑膜覆盖的比例越大,润滑性能越好。由此可见,HTSSLC基体中润滑层结构、润滑体特性及摩擦表面形貌特征都会对润滑边界膜分布及其在摩擦表面的覆盖率产生影响。

图128 HTSSLC润滑状态演化模型
工程中,从干摩擦到全膜润滑的转变过程(即边界润滑过程)是HTSSLC常处于的工况状态,也是其性能最不稳定的状态。因此,在此状态下对润滑膜覆盖率的控制可直接影响到对润滑性能的控制。在边界润滑过程中(见图128(b)),润滑膜存在于摩擦界面部分区域。
基于现代粘着理论,可以建立以下摩擦力模型。
F=τfAa+τbAb
(180)

则,摩擦表面总压力
P=σc(Aa+Ab)
(181)
式中,σc为接触部分平均压应力。
则,边界润滑膜覆盖率
ξf=Alu/A0
(182)
式中,Alu为润滑膜覆盖区域面积;A0为摩擦副名义接触面积。
若边界润滑膜覆盖区域接触部分与润滑膜覆盖区域的总面积成比例,则边界润滑状态下摩擦副之间的摩擦因数
Aa=kaAlu=ξfkaA0
(183)
Ab=(1-ξf)kaA0
式中,ka为比例系数。
式(183)表明,HTSSLC摩擦因数是润滑膜覆盖率的函数,且由于润滑膜剪切强度τf较基体材料剪切强度τb小,摩擦因数f随润滑膜覆盖率ξf的增大而减小。
6.5.2 高温发汗润滑膜覆盖率计算模型
6.5.2.1 模型
为了计算发汗润滑膜覆盖率ξf,将图128(b)的边界润滑状态简化为等效粗糙度表面与光滑刚性表面相接触(见图129)。

图129 高温发汗润滑膜覆盖率计算模型
由于接触部分总面积相对于名义接触面积来说比例很小,可忽略载荷对摩擦表面形貌的影响。假定析出摩擦表面的润滑体从表面形貌最低凹处依次开始填充,在表面微单元z(x,y)处填充的润滑体量
(184)
式中,ho为润滑体填充面的水平高度;A(x,y)为该表面微单元的面积。
在某些状况下,HTSSLC只占摩擦副总面积的一部分(例如,销-盘试验时,销为HTSSLC)。部分润滑体在热应力作用下从原来的孔隙中析出,其中一半析出到摩擦表面,润滑体总量
(185)
式中,ψ0为熔渗孔隙度;Δα为基体材料和润滑体热膨胀系数差值;Lh为润滑层厚度;β为HTSSLC摩擦表面面积占摩擦副总面积的比例,β≤1;ΔT为当因环境温度改变或摩擦导致HTSSLC温度上升;A0为摩擦副名义接触面积。
在摩擦表面分布的润滑体的总量应与HTSSLC析出润滑体的总量相等。
(186)
式中,mx为在取样表面长度方向的微单元数目;ny在取样表面宽度方向的微单元数目。
则,润滑膜的覆盖率
(187)
由式(184)~式(187)联立,可以计算基于摩擦表面形貌、润滑体特性、熔渗参数及材料孔隙结构的润滑膜覆盖率。
6.5.2.2 计算结果与验证
图130(a)和图130(b)为摩擦学试验后摩擦表面的SEM照片及润滑体Pb的分布。基于试验中摩擦表面形貌参数由式(156)生成具有相当表面粗糙度值的表面形貌见图130(c)。将试验条件代入式(184)及式(187),可以计算出覆盖率为33.46%,其分布情况见图130(d)。
计算时采用的材料及试验参数见表32~表34。基于表32~表34所提供的参数,当使润滑体在销与盘摩擦表面充分铺展时,通过分析,可得出图130(b)中Pb润滑膜在摩擦表面覆盖率为31.28%。可见,本研究团队建立的润滑膜覆盖率计算模型可有效预测HTSSLC润滑膜覆盖率。

表32 销试样试验参量

表33 盘试样试验参量

表34 实验条件
6.5.3 润滑层参数及工况条件对润滑膜覆盖率的影响
6.5.3.1 摩擦表面粗糙度对覆盖率的影响
图131为利用式(184)及式(187)计算出的具有不同粗糙度Ra值的表面及其滑膜覆盖率变化规律。

图131 表面粗糙度Ra值对润滑膜覆盖率的影响
从图131可以见到,润滑膜覆盖率大小受摩擦表面粗糙度的影响较大。当其他条件参数一定时,随着摩擦表面粗糙度Ra值减小,润滑膜覆盖率迅速上升。同时,摩擦表面粗糙度减小还可以降低摩擦表面接触应力幅值,减小边界润滑膜破裂及基体材料直接接触微凸体的粘着倾向。
由以上分析可知,在摩擦副制造过程中,通过采用合适的工艺参数适当减小摩擦副表面粗糙度Ra值可以有效提高摩擦表面边界润滑膜的覆盖率,改善摩擦副的摩擦磨损性能。
6.5.3.2 熔渗孔隙度的影响
【定义6熔渗孔隙度(infiltrationporosity)】 材料中熔渗有润滑体的孔隙体积与润滑层整体体积的比率。
在相同润滑层深度情况下,熔渗孔隙度越大,润滑层中所含的润滑体的量越大。但熔渗孔隙度受基体材料孔隙度限制。图132为在同样条件下,不同熔渗孔隙度的自润滑材料产生的润滑膜覆盖率曲线。

图132 熔渗孔隙度对润滑膜盖率的影响
从图132可以看出,随着熔渗孔隙度的提高,边界固体润滑膜的覆盖率增大。因此,适当提高材料的熔渗孔隙度,能够有效提高自润滑材料摩擦副的自润滑性能。
6.5.3.3 热膨胀系数差的影响
【定义7热膨胀系数差(differenceinthermalexpansioncoefficient)】 自润滑材料基体材料的热膨胀系数与润滑体材料热膨胀系数的差值。
HTSSLC工作时,由于润滑体的热膨胀系数大于基体材料,在环境温度提高或摩擦热作用下,润滑体在由于体积膨胀产生热应力作用下析出到摩擦表面。因此,当其他条件相同时,热膨胀系数差越大,析出摩擦表面的润滑体越多。
图133反映了热膨胀系数差对于润滑膜覆盖率的影响。可以看出,随着基体材料和润滑体热膨胀系数差值变大,覆盖率也不断变大。

图133 热膨胀系数差对润滑膜覆盖率的影响
6.5.3.4 润滑层深度对润滑膜覆盖率的影响
在制备HTSSLC时,润滑体通过熔浸工艺加入到基体材料中,在材料表层形成一定深度的润滑层。
【定义8润滑层深度(thicknessoflubricatinglayer)】 由材料表面到润滑体熔渗前沿的深度。
材料熔渗孔隙度一定时,润滑层深度决定了自润滑材料中润滑体的量。润滑层深度越大,自润滑材料中润滑体的量越多。
图134为不同润滑层深度下,摩擦表面润滑膜覆盖率的变化情况,可以看出,随润滑层深度增加,覆盖率不断增大。
由上述分析可知,通过选用合适的材料、改变制备工艺等手段可以有效提高摩擦副表面边界润滑膜的覆盖率,可以提高HTSSLC的自润滑性能。

图134 润滑层深度对润滑膜覆盖率影响
6.5.3.5 环境温度的影响
图135为摩擦环境温度对HTSSLC摩擦表面润滑膜覆盖率的影响曲线。
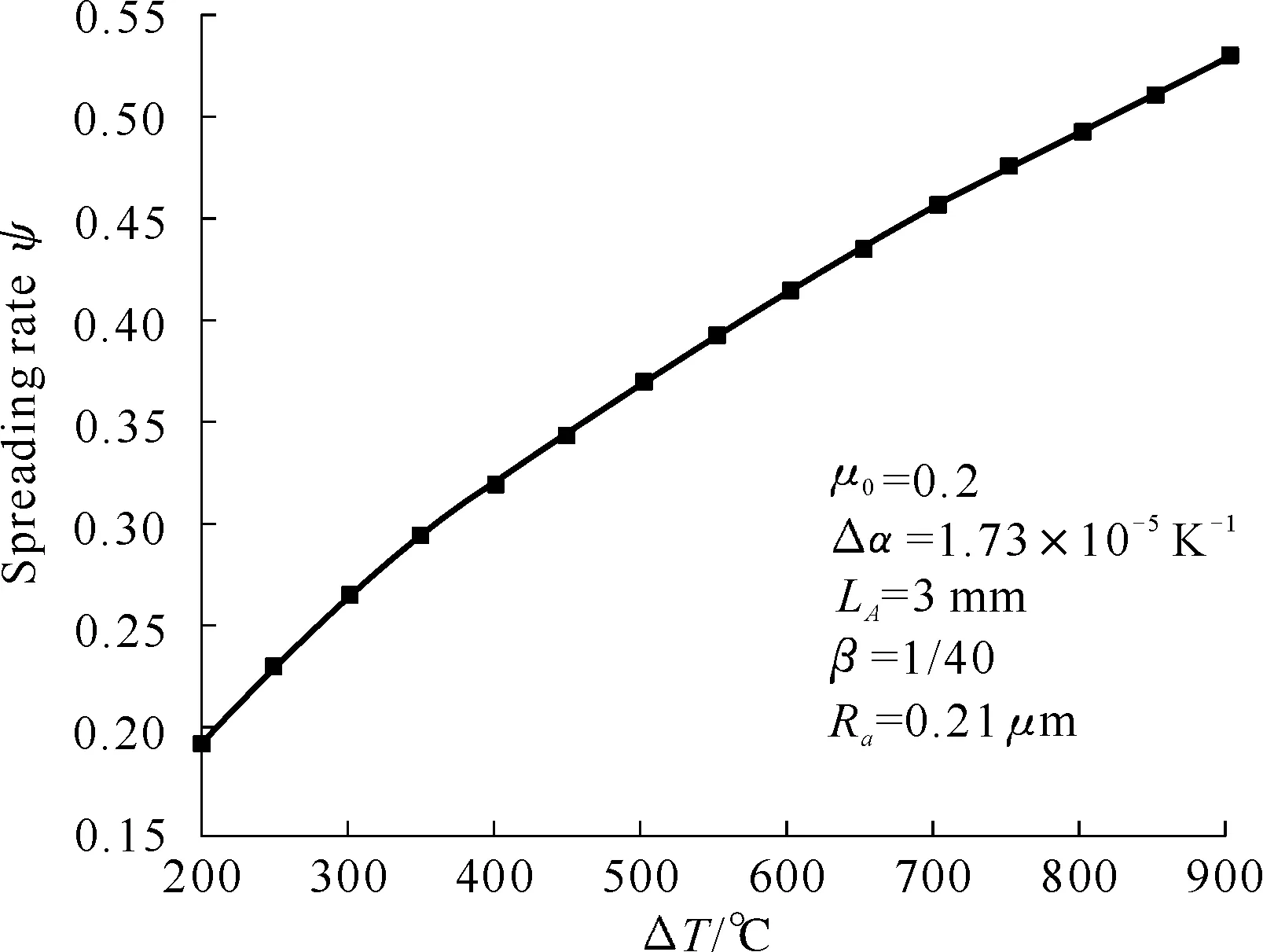
图135 环境温度对润滑膜覆盖率影响
从图135可以看出,随着环境温度的提高,润滑膜覆盖率随之增大。由于润滑体润滑性能受温度影响,具有一定的适用温度范围,同时提高摩擦副环境温度还会增加直接接触基体材料微凸体的粘着倾向。因此,环境温度对HTSSLC自润滑性能的影响需要进行综合考虑。
7 结论与讨论
7.1 结论
基于人体汗腺结构(SG)特征和发汗机理,以TiC陶瓷粉末和FeCrWMoV合金粉末为基体,以TiH2+CaCO3复合体为复合造孔剂,辅以Al2O3惰性弥散质点,制备出具有有序汗腺式微孔结构的金属陶瓷基体;采用真空压力熔渗法(Vacuum Pressure Infiltration,VPI)在汗腺式微孔中融入Pb-Sn-Ag-RE多元复合润滑体,制备出具有汗腺式微孔胞体结构的高温发汗自润滑材料(HTSSLC)。
基于汗腺式微孔胞体结构的HTSSLC,本研究团队开展了自补偿润滑机理、摩擦学特性、微观力学行为、接触强度等理论与试验研究,拓宽了该材料的应用范围。其主要研究成果与科学结论如下。
(1) 以TiH2+CaCO3复合体为造孔剂,以Al2O3为惰性弥散质点,以稀土氧化物Y2O3为硬质相界面净化剂,采用二次造孔法(Double Stage Pore-Forming Technique,DSP-FT),制备出表层孔隙形状规则有序、孔径分布均匀、互相贯通的网络状汗腺式结构金属陶瓷基体。
【结论1】 本研究团队制备的汗腺式胞体基体实现了高接触强度及固体润滑体填充空间的设计要求;当其孔隙度在15%以内时,其微观力学行为可作为连续介质处理。
(2) 基于人体汗腺结构和发汗机理,推导出汗腺式微孔分布表征模型(Pore Size Distribution Model,PSDM),并通过实验,验证了PSDM的理论值与实验值具有一致性。
(188)
【结论2】 本研究团队基于人体汗腺结构形态,构建出仿生汗腺结构材料体系及其数学模型,试验验证了仿生汗腺式微孔结构材料的可重构性。
(3) 基于HTSSLC基体厚壁均质有序的孔结构特征,引入λ特征值,建立了可表征各种孔结构形态的有序孔结构几何表征模型(Ordered Porous Structure Geometric Model,OPSGM),导出其相对密度广义表达式(Generalized Expression of Relative Density,GERD)和孔隙度广义表达式(Generalized Expression of Porosity,GEP)。
GERD和GEP拓宽了Gibson和Ashby表达式,使其不仅可用于多孔材料的强度计算,而且更能有效地反映出厚壁均质有序孔材料的孔隙度与压溃强度之间的关系。
【结论3】 当λ<0.4时,多胞体材料的相对密度和孔隙度不随λ值线性变化,此时,可将其视为连续介质体,材料具有较高强度。
(4) 建立了厚壁单胞体接触力学模型(Contact Mechanics Model of Thick-Wall Cellular Structure,CMMTWCS),并提出通过采用胞壁等效曲梁计算方法(Effective Curved Beam Computational Method,ECBCM)求解厚壁胞体的接触力学问题。
ECBCM不但可以将Hertz接触理论作为特例包含在内,而且避免了当量弹性模量法(equivalent modulus of elasticity)求解超越方程的困难,解决了混合理论法(mixed theory)无法求解孔洞周围局部应力分布的难题。
【结论4】 胞体孔隙度对其接触压力分布影响不大,但对胞壁弯曲变形和局部应力分布影响很大;故此,厚壁胞体接触压缩强度的影响因素不是接触变形,而是胞壁弯曲变形引起的胞体内部,尤其是孔口应力分布变化。
(5) 研究了汗腺式微孔胞体的胞孔结构及其分布形态对于多孔厚壁胞体接触稳定性的影响规律,特别是混合孔结构及其分布形态对于接触稳定性的影响规律,揭示出在接触条件下,胞体材料中正三角形、正四边形和正六边形微孔所占比例对于接触强度的影响规律;在此基础上,探讨了厚壁多孔厚壁胞体接触过载时裂纹萌生的位置及其扩展顺序。这一研究将为HTSSLC的工况适应性及其摩擦副载荷设计提供理论基础。
【结论5】 汗腺式微孔胞体孔结构及其分布形态直接影响到其孔结构的接触稳定性及其裂纹扩展方式。在孔隙度不变情况下,降低孔径和增大孔数,有助于提高厚壁胞体的接触强度;在所讨论的正三角形、正四边形和正六边形微孔结构形态系统中,正三角形孔对其接触强度影响最大。
(6) 建立了在切向力和法向力耦合作用下的厚壁胞体接触力学有限元分析模型,探讨了切向摩擦力对胞体接触表面应力、孔口应力及接触稳定性的影响。
【结论6】 切向力的存在将导致厚壁胞体接触强度下降,其裂纹萌生与扩展方向与切向力大小及其方向有关。
(7) 基于相图理论,设计制备了具有良好润滑特性和熔渗工艺性的复合润滑体。
【结论7】 自补偿润滑体熔融点及微孔基体润湿性对表面膜的形成及润滑性能影响较大,其理想的润滑体组分设计可基于相图理论及摩擦学试验数据获得。选用Ag-Pb-Ag-Cu-Re复合组分及合理配比,可设计出具有良好润湿性、扩散活性及润滑性能的复合自补偿润滑体。
(8) 提出了一种关于α因子混合律模型的预测模型,为了使α因子混合律模型适用工程要求,基于Hirsch模型,以α为参变量,建立了面向颗粒增强型复合材料的弹性模量修正Hirsch模型(Modified Hirsch Model of Elastic Modulus,MHMEM);研究了α与材料中各相成分体积百分比和弹性模量的函数关系。
【结论8】 理论结果与试验结果的一致性证明,本研究团队建立的SEEMEM精度高,避免了对试验数据的依赖,可有效地拓宽到均匀复合材料的弹性模量计算中。
(9) 推导出无需区分基体相和增强相的颗粒增强型均质复合材料热膨胀系数计算模型(Thermal Expansion Coefficient Model of Particel Reinforced Composites,TECMPRC),并将其与Kerner模型及实验值进行比较。
【结论9】 TECMPRC与实验值及Kerner模型具有良好的符合度,可有效地用以描述均质复合材料热膨胀特性。
(10) 研究了自补偿润滑胞体孔隙度与胞核变形量之间的相关性,工作温度对胞核变形量的影响,以及胞核组分对润滑体析出量的影响。
【结论10】 孔隙度及工作温度对胞核变形量有较大影响,而胞核组分及变形量又影响其润滑元素析出量;这种互耦性在很大程度上取决于胞体的组分设计其热参数性能。
(11) 在高温摩擦过程中,摩擦表面存在润滑体析出、富集及润滑膜形成与破坏的动态循环过程。
【结论11】 摩擦系数、摩擦表面形貌及润滑体分布的仿真模拟与摩擦学试验结果高度一致,证明元胞自动机模型(Automata Model,AM)可有效地模拟TECMPRC的动态摩擦过程,从而揭示出胞核润滑体的析出机理及其在摩擦表面的分布形态。
(12) 基于高温发汗润滑表面膜覆盖率与润滑性能之间的耦合关系,建立了高温发汗润滑膜覆盖率计算模型(Cover Rate Model of the Lubricating Film of the Gland Self-Lubricating Composite,CRMLFGSLC);揭示了摩擦副表面形貌、润滑层结构及材料参数、环境温度对润滑膜覆盖率的影响规律。
【结论12】 润滑膜覆盖率随材料基体孔隙度、润滑层深度和环境温度增加而增大;减小摩擦表面粗糙度,可以提高摩擦表面边界润滑膜的覆盖率。
(13) 作为一种新的材料结构,HTSSLC具有的高强内贯通有序微孔基体可作为摩擦学功能材料的理想载体,该载体中可浸渍具有不同性能的润滑体而组成特定润滑功能的发汗润滑功能体。
【结论13】 以BN-C-硅油复合胶体为润滑液,考察了应用原理与效果,在300 ℃的高温下,BN-C-油胶体的摩擦系数(约为0.13)远远低于纯硅油和BN-硅油胶体的摩擦系数。
以上研究表明,高温发汗自润滑材料(HTSSLC)有其独特的自润滑功能,特别是本研究团队所开发的高强度汗腺式微孔基体,不仅可利用材料基体强度,使其能够应用于高温重载工况环境的工程润滑;而且利用汗腺式微孔结构形态与尺度优势,存储具有不同特性的复合润滑粒子体,解决了特殊工况领域的自补偿润滑问题;更重要的是,由于HTSSLC中胞核润滑体是在摩擦热-应力驱动作用下沿基体(胞壁)中有序微孔(胞管)扩散至摩擦表面形成润滑膜;而摩擦愈严重的部位,往往其摩擦热-应力愈高,所导致其向表面扩散的驱动力愈大,从而实现了择优自补偿润滑;由此,本研究团队所开发的HTSSLC具有独特的抗磨与自补偿润滑的摩擦学功能。
7.2 高温发汗自润滑技术应用展望
7.2.1 工程应用性研究
本研究团队在高温复合自补偿润滑技术及其理论研究中开发出的高强度内贯通有序微孔金属陶瓷基体及具有良好润滑性的复合软金属润滑体,经二次复合后成为HTSSLC而制备出各种高温自润滑摩擦副。
目前,本研究团队已成功制备出高温自润滑球面轴承(Self-lubricating spherical bearings)(见图136(a))和高温自补偿润滑滑动轴承(Self-lubricating sliding bearings)(见图136(b)),并将其应用在冶炼高温热风炉及高温烧结炉。

图136 本研究团队开发的高温自润滑轴承
为了扩展其工业应用范围,本研究团队正基于热机设备的相关润滑特点,开发不同的高温润滑工程部件,例如汽轮机高温异形研磨板、高速发动机轴承及连铸机高温轴承产品,等等,已取得了良好的工程效果。
7.2.2 高温发汗润滑液的研究
由于高温固体润滑体的效能发挥环境温度相对地高,因而,开发出宽温域范围的润滑液是本研究团队的工作目标之一,其典型研究是BN-C-硅油复合润滑胶体的研究[79]。
BN和C具有相似的物理特性和晶体结构,基于经验电子理论(empirical electron theory,EET)对BN及BN-C复合物的价电子结构的分析表明,BN-C复合物的层间键能(lamellar bonds energy)(0.256 733 74 kJ·mol-1)小于BN的层间键能(0.331 294 92 kJ·mol-1),因而BN-C复合物更易发生层间滑移,导致摩擦系数更小。
基于上述发现,本研究团队制备出可作为高温润滑液填充到发汗材料基体之中的BN-C-硅油胶体,以拓宽润滑温度范围,目标是实现从室温~300 ℃范围的发汗润滑功能。
图137为以二甲基硅油为研磨介质制备出的BN-C-硅油复合胶体,其中纳米态BN-C复合颗粒均匀分散于硅油之中;图138为胶粒能谱。可以看出,在胶粒成分谱线中除含有B,C,N等3种元素的峰值外,还含有Si和O等两种元素的峰值;Si元素来自硅油分子,而O元素一部分来自硅油分子,另一部分来自样品所受氧化污染。虽然在测试前已对胶粒进行了分离除油,但能谱分析仍能发现明显存在O元素,可见硅油对胶粒的包覆比较紧密。由于表面张力较低的硅油对BN-C复合颗粒的强包覆,避免了BN-C复合颗粒的团聚,起到辅助表面活性剂分散的作用,使其不易发生二次团聚,使其易于浸渍于汗腺微孔中作为发汗润滑液。

图137 BN-C-硅油胶体的微粒分布形态

图138 复合胶粒成分能谱
图139为浸渍在金属陶瓷基微孔中作为润滑胞核的BN-C复合胶体分布形态,图140为浸渍BN-C复合胶体后材料在300 ℃工况下摩擦表面膜形态,图141为BN-C-硅油复合胶体与其基础润滑油在不同温度下的摩擦系数。可以看出,从100 ℃~300 ℃的较宽温度范围内,BN-C-硅油胶体的润滑性比BN-硅油胶体和纯硅油的润滑性都好,尤其是在300 ℃高温下,BN-C-硅油胶体的摩擦系数(约为0.13)远远低于纯硅油和BN-硅油胶体的摩擦系数。

图139 BN-C-硅油胶体的金属陶瓷微孔中的分布形态

图140 浸渍BN-C-硅油胶体后的磨损表面润滑膜

图141 在不同温度下的纯硅油与两种胶体摩擦系数
另一研究是利用高强度内贯通汗腺式微孔金属陶瓷基体为载体,研究磁流润滑液与微磁场互耦作用下的微循环润滑功能,创新出摩擦学复合功能体,以满足特殊工况设备的润滑与密封双功能要求。目前,该内容正在中国国家自然科学基金资助下开展研究。
以上研究表明,由于HTSSLC基体具有高接触强度、有序微孔结构形态及其尺度优势,因此,可作为摩擦学功能体的载体,通过存储具有不同特性的复合润滑粒子体,以仿生原理解决不同工况领域的润滑自补偿及其控制问题。
[1] Rayleigh L.Notes on the Theory of Lubrication.Philosophical Magazine,1918,35(6):1-12.
[2] Panzera T H,Rubio J C,Bowen C R,et al.Microstructural Design of Materials for Aerostatic Bearings.Cement & Concrete Composites,2008(30):649-660.
[3] 雷源忠,黎 明.21世纪的制造科学.中国机械工程,1999,10(6):689-691.
Lei Yuanzhong,Li Ming.Manufacture Science in 21th Century.China Mechanical Engineering,1999,10(6):689-691.
[4] 邓宝清,任露泉,苏 岩,等.模拟活塞缸套摩擦副的仿生非光滑表面的摩擦学研究.吉林大学学报(工学版),2004,34(1):79-84.
Deng Baoqing,Ren Luquan,Su Yan,et al.Tribological Study on Bionically Unsmoothed Surface Modeling Piston-Cylinder Friction Pair.Journal of Jilin University of Technology(Engineering Edition),2004,34(1):79-84.
[5] 金卓仁,程继贵,夏永红,等.梯度自润滑滑动轴承的研制.机械工程学报,2001,37(3):81-84.
Jin Zhuoren,Cheng Jigui,Xia Yonghong,et al.Study on the Gradient self- Lubfricating Slidinng Bearings.Chinese Journal of Mechanical Engineering,2001,37(3):81-84.
[6] 张建华,陶德华,付尚发,等.新型人工关节仿生润滑系统设计及滑液摩擦学特性研究.摩擦学学报,2003,23(6):500-503.
Zhang Jianhua,Tao Dehua,Fu Shangfa,et al.Design of Bionic Lubrication System of Artificial Joints and Study on the Tribological Performance of a Synthetic Synovial Fluid.Tribology,2003,23(6):500-503.
[7] 张建华,陶德华.仿生润滑技术研究及其应用探讨.润滑与密封,2004(6):99-100.
Zhang Jianhua,Tao Dehua.Discussion on Bionic Lubrication Technology and its Applications.Lubrication Engineering,2004(6):99-100.
[8] 刘国敏.蚯蚓体表减粘降阻功能耦合仿生研究[博士学位论文].长春:吉林大学,2009.
Liu Guomin.Coupling Bionic Research on the Adhesion and Resistance Reduction of the Earthworm Surface[Ph. D Thesis].Changchun:Jilin University,2009.
[9] 王绍敏.仿生结构化船体表面减阻性能分析.舰船科学技术,2010,32(5):11-13.
Wang Shaomin.Biomimetic Structure of the Hull Surface Drag Reduction Performance Analysis.Ship Science and Technology,2010,32(5):11-13.
[10] Liu Z M.Elevated Temperature Diffusion self-Lubricating Mechanisms of a Novel Cermet Sinter with Orderly Micro-Pores.Wear,2007(262):600-606.
[11] Dowson D,Wright V.Bio-Tribology//Proceedings of the Conference on the Rheology of Lubrication Organised by the Institute of Petroleum,1973:81-88.
[12] Chen Jie,Lu Xiyun.Numerical Investigation of the non-Newtonian Blood Flow in a Bifurcation Model with a non-Planar Branch.Journal of Biomechanics,2004(37):1899-1911.
[13] 龚中良,谭建平.人体血液及其润滑性能研究的现状与展望.润滑与密封,2007,32(10):123-127.
Gong Zhongliang,Tan Jianping.Present Situation and Prospects of the Research on Human Blood and its Lubricity.Lubrication Engineering,2007,32(10):123-127.
[14] Tanaka E,Michael S D,Kotaro T,et al.Lubrication of the Temporomandibular Joint.Annals of Biomedical Engineering,2008,36(1):14-29.
[15] Mattheck C,Burkhardt S.A new Method of Structure Shape Optimization based on Biological Growth.International Journal of Fatigue,1990,12(3):185-190.
[16] 李安琪,任露泉,陈秉聪,等.蚯蚓体表液的组成及其减粘脱土机理分析.农业工程学报,1990,6(3):8-14.
Li Anqi,Ren Luquan,Chen Bingcong,et al.Constitution and Mechanism Analysis of Reducing Soil Adhesion for the Body Surface Liquid of Earthworms.Transactions of the Chinese Society of Agricultural Engineering,1990,6(3):8-14.
[17] 许亚婷,李建桥,孙久荣,等.蚯蚓体表形貌及润湿性的研究.华中农业大学学报,2005(10):40-43.
Xu Yating,Li Jianqiao,Sun Jiurong,et al.Research on the Surface Feature of Earthworm and its Wettability.Journal of Huazhong Agricultural University,2005(10):40-43.
[18] Gravish N,Wilkinson M,Sponberg S,et al.Rate-Dependent Frictional Adhesion in Natural and Synthetic Gecko Setae.Journal of the Royal Society Interface,2010,7(43):259-269.
[19] Ryshkewitch E.Compression Strength of Porous Sintered Alumina and Zirconia.Journal of the American Ceramic Society,1953,36(2):65-68.
[20] 韩风麟.美国MPIF标准35“粉末冶金自润滑轴承材料标准”1998年修订简介.粉末冶金工业,2000,10(3):36-46.
Han Fenglin.Introduction of MPIF Standard 35(US)‘Materials Standards for PM self-Lubricating Bearing’ Revised in 1998.Powder Metallurgy Industry,2000,10(3):36-46.
[21] Kuczynski G C.Sintering and Related Phenomena.Materiala Science Research,1973(6):217-217.
[22] 王砚军.高温发汗自润滑金属陶瓷的制备、表征及摩擦学特性研究[博士学位论文].武汉:武汉理工大学,2008.
Wang Yanjun.Study on Fabrication,Characterization and Tribological Properties of high Temperature self-Lubrication Metal Ceramics with Sweat Gland Structure[Ph. D Thesis].Wuhan:Wuhan University of Technology,2008.
[23] Zener C.Imperfections in Nearly Perfect Crystals.New York:John Wiley and Sons Inc.,1952:289-290.
[24] 崔国文.缺陷扩散与烧结.北京:清华大学出版社,1990:182-188.
Cui Guowen.Defect Diffusion and Sintering.Beijing:Tsinghua University Press,1990:182-188.
[25] 施剑林.固相烧结(Ⅱ)——粗化与致密化关系及物质传输途径.硅酸盐学报,1997,25(6):657-667.
Shi Jianlin.Solid State Sintering(Ⅱ)——Relation Between Coarsening and Densification and Mass Transport Path. Journal of the Chinese Ceramic Society,1997,25(6):657-667.
[26] 果世驹.粉末烧结理论.北京:冶金工业出版社,1998:248-256.
Guo Shiju.Powder Sintering Theory.Beijing:Metallurgical Industry Press,1998:248-256.
[27] 宝鸡有色金属研究所编著.粉末冶金多孔材料(上).北京:冶金工业出版社,1978:105-106.
Baoji Nonferrous Metal Research Institute Ed.Powder Metallurgic Porous Material(Ⅰ).Beijing:Metallurgical Industry Press,1978:105-106.
[28] 薛明俊,刘智恩,沈 凯.钛酸铝多孔陶瓷的研制.中国陶瓷,1995,31(2):17-20.
Xue Mingjun,Liu Zhien,Shen Kai.Study of Porous Aluminum Titanate Ceramics.China Ceramics,1995,31(2):17-20.
[29] 周益春.材料固体力学.北京:科学出版社,2005.
Zhou Yichun.Solid Mechanics in Materials.Beijing:Science Press,2005.
[30] Gibson L J,Ashby M F.Cellular Solids:Structures and Mroperties(2nd ed).Cambridge:Cambridge University Press,1997.
[31] Bedford A,Drumheller D S.Theories of Immiscible and Structured Mixtures.International Journal of Engineering Science,1983,21(8):863-960.
[32] Johnson K L.Contact Mechanics.Cambridge:Cambridge University Press,1985.
[33] 李春胜,黄德彬.机械工程材料手册.北京:电子工业出版社,2007.
Li Chunsheng,Huang Debin.Handbook of Materials for Mechanical Engineering.Beijing:Electronic Industry Press,2007.
[34] 张后全,唐春安,宋 力,等.布孔方式对孔洞材料宏观力学性能影响的研究.应用力学学报,2006,23(1):62-67.
Zhang Houquan,Tang Chunan,Song Li,et al.Influence of Hole Distribution on Macroscopic Mechanical Behavior of Perforated Materials.Chinese Journal of Applied Mechanics,2006,23(1):62-67.
[35] 解 芳,刘佐民.厚壁胞体多孔结构接触强度研究.固体力学学报,2010,31(3):296-301.
Xie Fang,Liu Zuomin.Study on Contact Strength of Thick-Walled Cellular Structures.Chinese Journal of Solid Mechanics,2010,31(3):296-301.
[36] 段进超,唐春安,常 旭,等.单轴压缩下含孔脆性材料的力学行为研究.岩土力学,2006,27(8):1416-1420.
Duan Jinchao,Tang Chunan,Chang Xu,et al.Study on Mechanics Behavior of Containing Holes in Brittle Material Subjected to Uniaxial Compression.Rock and Soil Mechanics,2006,27(8):1416-1420.
[37] 解 芳.高温发汗润滑胞体的接触稳定性研究[博士学位论文].武汉:武汉理工大学,2011.
Xie Fang.Study on Contact Stability of high Temperature Sweating and Lubricating Cellular Solids[Ph. D Thesis].Wuhan:Wuhan University of Technology,2011.
[38] 罗 虹,刘家浚.空心圆柱滚动体接触状况的分析研究.摩擦学学报,1997,3(17):253-259.
Luo Hong,Liu Jiajun.Analysis of Contact Status on Hollow Cylindrical Roller.Tribology,1997,3(17):253-259.
[39] 颜志光.新型润滑材料与润滑技术实用手册.北京:国防工业出版社,1999.
Yan Zhiguang.Manual of new Lubricating Material and Technology.Beijing:National Defence Industry Press,1999.
[40] 袁章福,柯家骏,李 晶.金属及合金的表面张力.北京:科学出版社,2006.
Yuan Zhangfu,Ke Jiajun,Li Jing.Surface Tension of Metal and Alloy.Beijing:Science Press,2006.
[41] 张启运,庄鸿寿.钎焊手册.北京:机械工业出版社,1999.
Zhang Qiyun,Zhuang Hongshou.Brazing and Soldering Manual.Beijing:China Machine Press,1999.
[42] 王静波,孟秀坤,黄业中,等.钨酸铅高温润滑特性的研究.摩擦学学报,1992,12(1):81-87.
Wang Jingbo,Meng Xiukun,Huang Yezhong,et al.Study on the high Temperature Lubricating Properties of the Lead Tungstate.Tribology,1992,12(1):81-87.
[43] Sliney H E,Spalvins T.The Effect of Ion-Plated Silver and Sliding Friction on Tensile Stress-Induced Cracking in Aluminum Oxide.Lub. Eng.,1992,49:153-159.
[44] Erdemir A,Fenske G R,Nichols F A,et al.Solid Lubrication of Ceramic Surfaces by IAD-Silver Coatings for Heat Engine Applications.Tribo Trans.,1990,33(4):511-518.
[45] 黄 金.融盐自发浸渗过程与微米级多孔陶瓷基复合相变储能材料研究[博士学位论文].广州:广东工业大学,2005.
Huang Jin.Study on Composite Phase Change Energy Storage Materials by Molten Salt Spontaneous Infiltrating Porous Ceramic Performs[Ph. D Thesis].Guangzhou:Guangdong University of Technology,2005.
[46] 徐志锋,余 欢,蔡长春,等.真空变压力浸渗法制备高体积分数SiCp/Al复合材料.中国有色金属学报,2006,16(9):1551-1556.
Xu Zhifeng,Yu Huan,Cai Changchun,et al.Preparation of high Volume Fraction SiCp/Al Composites by Vacuum-Adjustable Pressure Infiltration Process.Chinese Journal of Nonferrous Metals,2006,16(9):1551-1556.
[47] 顾惕人,朱涉瑶,李外郎,等.表面化学.北京:科学出版社,1994:1-33.
Gu Tiren,Zhu Sheyao,Li Wailang,et al.Surface Chemical.Beijing:Science Press,1994:1-33.
[48] Honig R E,Kramer D A.Vapour Pressure Data for the Solid and Liquid Elements.Reaction Kinetics and Catalysis Letters,1969,30(06):285-305.
[49] Margrave J.The Characterization of high-Temperature Vapors.New York:John Wiley and Sons. Inc.,1967:115-129.
[50] 方洪渊.简明钎焊工手册.北京:机械工业出版社,2001:51-65.
Fang Hongyuan.A Concise Manual on Brazing and Soldering.Beijing:China Machine Press,2001:51-65.
[51] 叶润清,罗 乐.Sn62Pb36Ag2焊料的微结构粗化.功能材料与器件学报,1999,5(4):327-331.
Ye Runqing,Luo Le.Microstructure Coarsening of Sn62Pb36Ag2 Solder.Journal of Functional Materials and Devices,1999,5(4):327-331.
[52] Wang L,Yu D Q,Zhao J,et al.Improvement of Wettability and Tensile Property in Sn-Ag-RE Lead-Free Solder Alloy.Materials Letters,2002,56(6):1039-1042.
[53] Yu D Q,Zhao J,Wang L.Improvement on the Microstructure Stability,Mechanical and Wetting Properties of Sn-Ag-Cu Lead-Free Solder with the Addition of Rare Earth Elements.Journal of Alloys and Compounds,2004,376(1-2):170-175.
[54] Voigt W.Uber die Beziehung Zwischen den Beiden Elastizitatskonstanten Isotroper Korper.Wied Ann,1889(38):573-587.
[55] Reuss A.Berechnung Der Fliessgrenze von Mischkristallen auf Grund der Plastizitatstheorie.Mathematic and Mechanic,1929,9:49-58.
[56] G Kalaprasad,K Joseph,S Thomas,et al.Theoretical Modeling of Tensile Properties of Short Sisal Fibre-Reinforced Low-density Polyethylene Composites.Journal of Materials Science,1997,32(16) :4261-4267.
[57] 卢 平,刘佐民.基于α因子的复合材料弹性模量混合律模型.武汉理工大学学报,2008,30(9):19-23.
Lu Ping,Liu Zuomin.Mixed-Mode of Elastic Modulus Composites Based on the α Factor.Journal of Wuhan University of Technology,2008,30(9):19-23.
[58] 柏振海,黎文献,罗兵辉,等.一种复合材料弹性模量的计算方法.中南大学学报(自然科学版),2006,37(3):438-443.
Bai Zhenhai,Li Wenxian,Luo Binghui,et al.A Calculation Method of Elastic Modulus of Composites.Journal of Central South University(Science and Technology),2006,37(3):438-443.
[59] 李进军,于家康.SiC 颗粒增强Al 基复合材料的热膨胀性能.陕西科技大学学报,2007,25(2):74-78.
Li Jinjun,Yu Jiakang.Thermal Expansion Properties of Silicon Carbide Particle Reinforced Aluminum.Journal of Shanxi University of Science & Technology,2007,25(2):74-78.
[60] Hale D K.Physical-Properties of Composite-Materials.Journal of Materials Science,1976,11(11):2105-2141.
[61] Eshelby J D.The Elastic Field Outside an Ellipsoidal Inclusion.Pro. Roy. Soc.,1959,252(1271):561-569.
[62] Eshelby J D.The Determination of the Elastic Field of an Ellipsoidal Inclusion,and Related Problems.Proc. Roy. Soc(A),1957,241(1226):376-396.
[63] 徐芝纶.弹性力学简明教程.北京:高等教育出版社,1983.
Xu Zhilun.A Concise Course on Elasticity.Beijing:Higher Education Press,1983.
[64] 卢 平,刘佐民.Hirsch模型的复合材料弹性模量的改进算法.中国机械工程,2008,19(23):2852-2859.
Lu Ping,Liu Zuomin.An Improved Method of Elastic Modulus of Composites Based on Hirsch Model.China Mechanical Engineering,2008,19(23):2852-2859.
[65] 修子扬,宋美慧,孙东立等.增强体含量对Sip/LD11复合材料热物理性能影响.材料科学与工艺,2005,13(2):170-174.
Xiu Ziyang,Song Meihui,Sun Dongli,et al.The Influence of the Volume Fraction of Reinforcements onThermo-Physical Properties of Sip/LD11 Composites.Material Science and Technology,2005,13(2):170-174.
[66] Fournier R,Fournier S.Sheet Metal Handbook.New York:HP Books,1989.
[67] Kerner E H.The Elastic and Thermo-Elastic Properties of Composite Media.Proc. Phys. Soc.(B),1956,69(8):808-813.
[68] Turner P S.Thermal-Expansion Stresses in Reinforced Plastics.Journal of Research National Bureau of Standards,1946,37(4):239-250.
[69] Dugdale D S.Yielding of Steel Sheets Containing Slits.J. Mech. Phy. Sol., 1960,8(2):100-104.
[70] James A M,Lord M P.Macmillan’s Chemical and Physical Data.London:UK,1992.
[71] 张一兵,燕松山,刘佐民.高温自润滑包覆体胞热驱模型的研究.武汉理工大学学报,2006,28(6):20-23.
Zhang Yibing,Yan Songshan,Liu Zuomin.Study on the Heat-Driving Mechanism of self-Lubricating Covered Model at Elevated Temperature.Journal of Wuhan University of Technology,2006,28(6):20-23.
[72] Shuaib M,Davies T J.Wear Behaviour of a REFEL SiC Containing Fluorides up to 900°C.Wear,2001,249(1-2):20-30.
[73] 祝玉学,赵学龙.物理系统的元胞自动机模拟.北京:清华大学出版社,2003.
Zhu Yuxue,Zhao Xuelong.Celluar Automata Modeling of Physical Systems.Beijing:Tsinghua University Press,2003.
[74] Komvopoulos K.Effects of Multi-Scale Roughness and Frictional Heating on Solid Body Contact Deformation.Mecanique C R,2008,336(1):149-162.
[75] Hassan Zahouani,François Sidoroff.Rough Surfaces and Elasto-Plastic Contacts.C. R. Acad. Sci.,2001,2(4):709-715.
[76] Halling J,著.上海交通大学摩擦学研究室,译.摩擦学原理.北京:机械工业出版社,1981.
Halling J.Tribology Research Center of Shanghai Jiaotong University(Tran.).Principle of Tribology.Beijing:China Machine Press,1981.
[77] 侯镇冰.固体热传导.上海:上海科学技术出版社,1984.
Hou Zhenbing.Heat Conduction in Solids.Shanghai:Shanghai Science and Technology Press,1984.
[78] J.H. Kang,I.W. Park,J.S. Jae,et al.A Study on a Die Wear Model Considering Thermal Softening(I):Construction of the Wear Model.Journal of Materials Processing Technology,1999,96(1-3):53-58.
[79] 郭 红.BN-C硅油高温润滑胶体制备及其性能研究[博士学位论文].武汉:武汉理工大学,2008.
Guo Hong.Study of the Preparation of BN-C-Silicone Oil Composite Colloid and Its Lubricating Properties at High Temperature[Ph. D Thesis].Wuhan:Wuhan University of Technology,2008.
