支持向量机方法在烟叶可用性预测中的应用

章平泉，杜秀敏，金岚峰，陈兆华，金殿明

（江苏中烟工业有限责任公司淮阴卷烟厂，江苏 淮安 223002）

不同的学者[1-2]对烟叶的可用性有不同的认识，一般认为可用性包括烟叶本身主观的特征和客观的要求，是可变的，是某种烟叶在特定的厂家的特定的卷烟制品中满足其配方需求的程度[3]。目前烟叶可用性问题主要表现在以下几个方面：烟叶香味风格尚不能完全满足中式卷烟对原料的需要；部分烟叶的化学成分不够协调；一些烟叶的外观质量和内在质量不一致；烟叶质量的稳定性较差。因此，如何提高和评价烟叶可用性是一项综合性的系统工程[4]。随着新理论、新技术的发展，人们提出了许多新模型和方法应用于烟叶可用性评价[5-9]，但这些方法都存在着评价指标适宜值及评价因子权重难于客观确定等不足。

支持向量机（Support Vector Machine，SVM）是建立在VC（Vapnik Chervonenkis）维理论和结构风险最小化准则基础上的一种新型机器学习方法[10]。与神经网络等传统机器学习方法相比，SVM具有小样本学习、泛化能力强等特点，能有效地避免过学习、局部极小点以及“维数灾难”等问题[11]。目前，并没有SVM应用于烟叶可用性预测的相关文献报道。因此，本研究尝试建立烟叶可用性SVM模型，并对模型的预测准确性进行验证，以便更好地进行烟叶可用性评价，为卷烟产品配方维护和烟叶分组加工提供参考。

1 SVM分类模型

1.1 两类分类

给定训练集

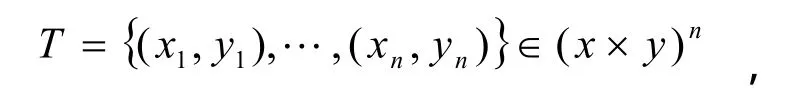
超平面w·x+b=0能将两类样本正确区分，并使分类间隔最大的优化问题可表示为：

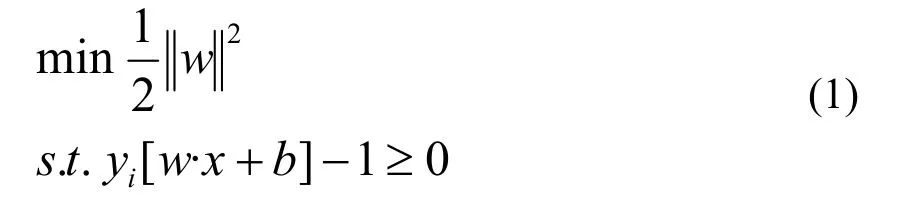
当训练集线性不可分时，任何超平面都必有划分错误的样本点。为此，引入松弛变量ξi≥0(i=1,…,n)，约束条件为yi[w·x+b]+ξi− 1≥0(i=1,2,…,n)，同时引进惩罚参数C作为对错分样本点的惩罚，此时优化函数为:

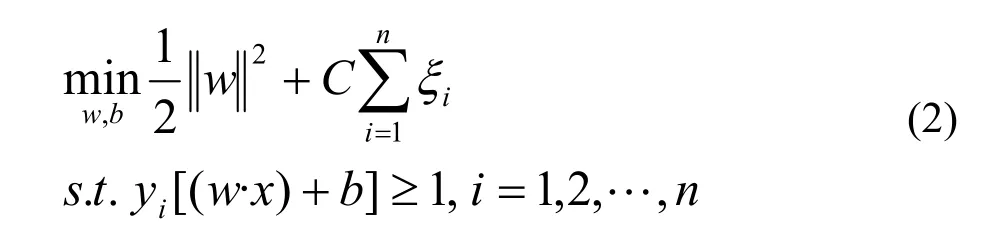
优化(2)式的对偶问题为：

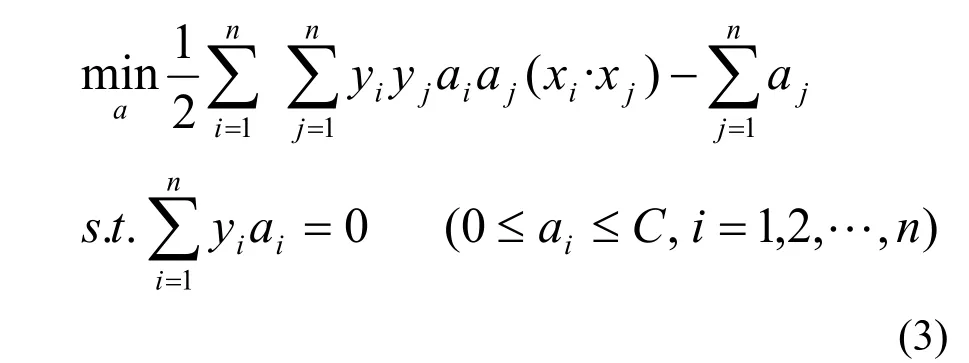
由Kuhn-Tucker定理可知，对偶变量与约束的乘积为0，即：

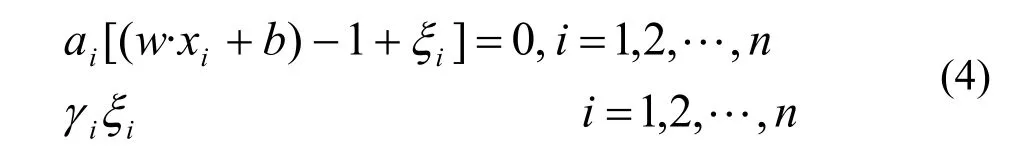
如果ai=0，样本xi称为非支持向量；若ai＞0样本xi称为支持向量，因此，最后得判别函数为：

对于非线性分类，使用非线性映射Ø把数据从原空间Rn映射到一个高维特征空间ω，在高维特征空间ω上建立优化平面。此时，在非线性情况下支持向量机对分类问题称为最大化函数：

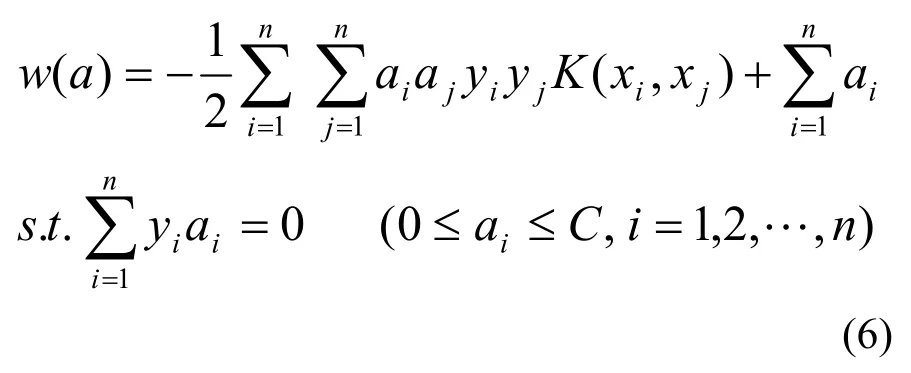
此时决策面为：

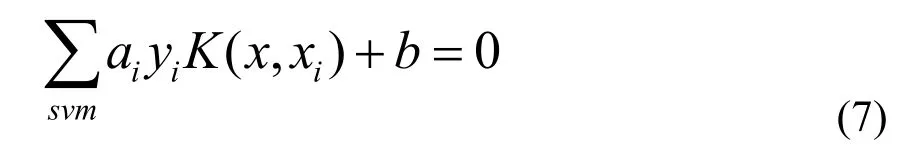
最后得决策函数为：

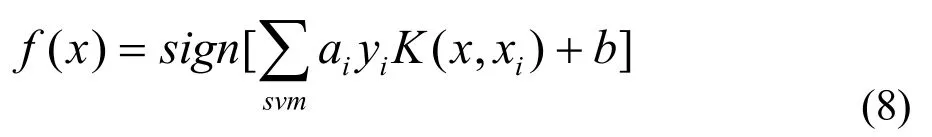
其中K(x,xi)为核函数，核函数的选取应使其成为特征空间的一个点积，即存在函数Ø，使得K(x,xi)=φ(x) φ(xi)，常用的核函数：

其中γ,r, 和d为核函数参数。

1.2 多类分类

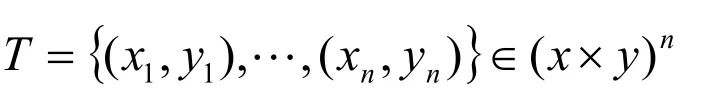
对于训练集中第i和j类，需要解决以下二分类问题：

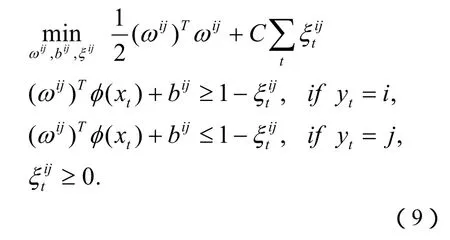
通过(6)式求出最终的决策函数为：

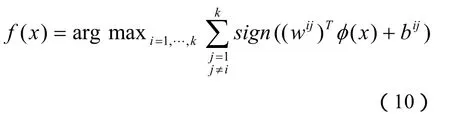
2 仿真实验

2.1 数据来源和预处理

刘国顺等[5]用化学成分（总氮、总糖、还原糖、施木克值、总植物碱和钾）和物理特性（单叶重、含梗率、叶质重、平衡含水率和填充力）作为分类参数，运用主成分分析和聚类分析方法，对 44个烟叶样本进行了分类，根据综合得分把所有烟叶样本分为5组。为了清晰区分样品的分类属性，根据文献[5]的烟叶可用性评价结果，去除8和9号样本，将剩余42个烟叶样本分为4类，即可用性差（记为第 1类，共 8个样本）、可用性较差（记为第 2类，共8个样本）、可用性较好（记为第3类，共14个样本）和可用性好（记为第4类，共12个样本）（表1）。

从第1类至第4类样品中分别随机选取2、2、3和3个共计10个样品组成预测集样本，将其余32个样品组成训练集样本建立烟叶可用性SVM预测模型，并对预测集样本分类属性进行预测。为了消除不同物理量纲的影响，对所有物理特性和化学指标按照x'=(x−min(x))/(max(x)−min(x))进行规范化处理，其中x'为某指标规范后的数值，min(x)=min(x1,x2,…xn);max(x)=max(x1,x2,…xn)。采用libsvm2.9软件[12]建立SVM预测模型。

2.2 结果

以文献[5]中32个原始数据为训练样本集，用Fisher法[13]作模式识别投影图。分别选取多项式函数、sigmoid函数以及RBF函数作为核函数建立SVM预测模型，采用k-折交叉验证法确定最优参数，并与Fisher法分析结果进行对比。结果如图1和表2。

从图1可以看出，Fisher法训练分类结果较好，但对预测集样本的预测准确率只有70%。从表2可以看出，SVM方法对预测集样本的预测准确率达到了80%～90%，明显优于前者，且以RBF为核函数建立的SVM模型预测结果最好，对训练集和预测集样本的预测准确率分别为84.38%和90%，表现出较强的泛化能力（建模参数为C=4，γ=0.25，ε=0.001），这可能是由于RBF可调参数少，在一般光滑性假设条件下具有良好的性能所致[14]。但另一方面，本研究建立的烟叶可用性SVM预测模型对训练集和预测集的预测准确性仍有较大的提升空间，其原因可能有以下几点：①试验所选取的物理特性和化学成分只是影响烟叶可用性的一部分，而不是全部；②模型选择影响SVM的性能；③预测准确性依赖于训练集和预测集样本的选取以及训练集样本的来源，数量及其代表性。

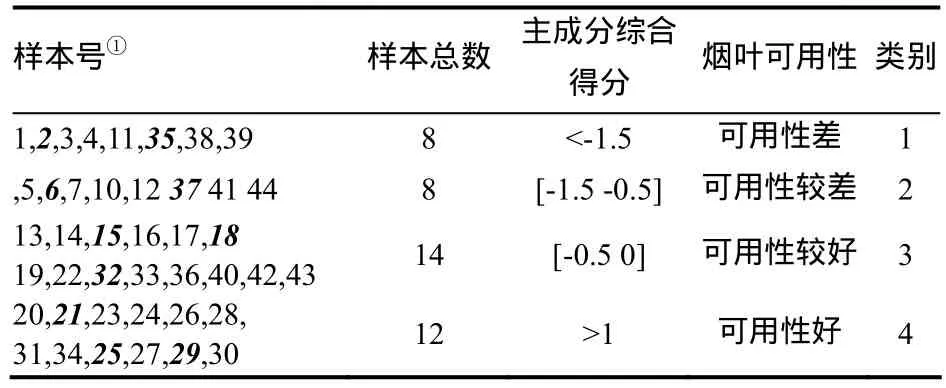
表1 烟叶可用性分组结果Table1 Grouping results of tobacco leaf usability

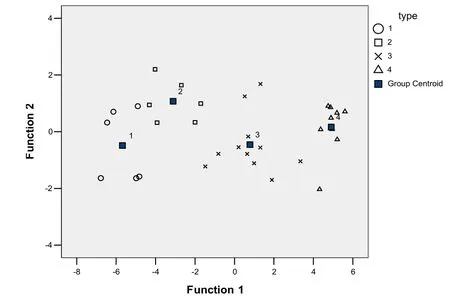
图1 烟叶可用性的Fisher法分类投影图Fig.1 The class projection chart of tobacco leaf usability forecast with Fisher method

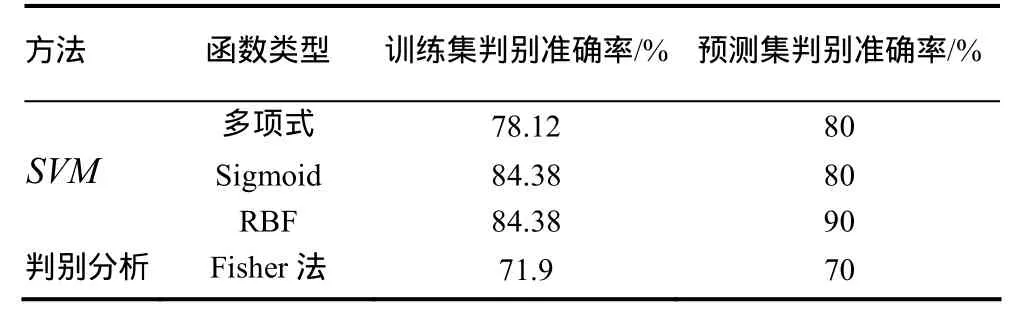
表2 不同方法对预测集样本预测结果的对比Table2 Comparison prediction results of forecast samples with different methods

3 小 结

运用不同的核函数建立烟叶可用性SVM预测模型，并与Fisher法分析结果进行对比。分析结果表明，烟叶可用性SVM预测模型比Fisher法分析结果均好，且以RBF为核函数建立的SVM分类预测模型能更佳地反映烟叶可用性与物理和化学指标之间的非线性关系。如何建立更好地评价烟叶可用性SVM分类预测模型，并准确地对烟叶可用性进行预测，还需综合训练集样本选择、评价指标的确定及SVM模型参数的选择才能进一步、合理地确定。

[1]左天觉．烟草的生产，生理和生物化学[M].朱尊权，等，译．上海：远东出版社，1993.

[2]朱尊权．烟叶的可用性与卷烟的安全性[J].烟草科技，2000（8）：3-6.

[3]唐远驹．关于烟叶的可用性问题[J].中国烟草科学，2007，28（1）：1-5.

[4]邓小华.湖南烤烟区域特征及质量评价指标间关系研究[D].长沙：湖南农业大学，2007：12.

[5]刘国顺，杨永锋，凌爱芬.应用主成分分析和聚类分析评价烤烟叶位间质量差异[C]//中国烟草学会 2006年学术年会论文集，2007.

[6]王欣.湖北烟区烤烟质量综合评价及与国内外优质烤烟的差异分析[D].郑州：河南农业大学，2008.

[7]薛超群，尹启生，王信民.模糊综合评判在化学成分评价烟叶可用性中的应用[J].烟草科技，2007（4）：62-64.

[8]丁云生，何悦，曹金丽.大理州烤烟主要化学成分特征及其可用性分析[J].中国烟草科学，2009，30（3）：13-18.

[9]张永安.提高上部烟叶可用性的化控技术研究[D].合肥：安徽农业大学，2004：6.

[10]Vapnik V．统计学习理论的本质[M].北京：清华大学出版社，2000．

[11]Vapnik V．An overview of statistical learning theory[J]．IEEE Transactions on Neural Netwoks，1999，10(5): 988-999．

[12]Chih Chung Chang, Chih Jen Lin.LIBSVM-a library for support vector machines [EB/OL]. [2010-1-10]http://www.csie.ntu.edu.tw/～cjlin/libsvm.

[13]张文彤.SPSS 11统计分析教程（高级篇）[M].北京：北京希望电子出版社，2002.

[14]田盛丰，黄厚宽.回归型支持向量机的简化算法[J].软件学报，2002，13（6）：1169-1172.