磁流体热疗中超顺磁性磁流体耗散功率

夏 丹, 何晓雄, 陈红丽

(1.合肥工业大学 电子科学与应用物理学院,安徽 合肥 230009;2.中国科学院 等离子体物理研究所,安徽 合肥 230031;3.中国科学技术大学 核科学技术学院,安徽合肥 230027)

磁流体热疗中超顺磁性磁流体耗散功率

夏 丹1, 何晓雄1, 陈红丽2,3

(1.合肥工业大学 电子科学与应用物理学院,安徽 合肥 230009;2.中国科学院 等离子体物理研究所,安徽 合肥 230031;3.中国科学技术大学 核科学技术学院,安徽合肥 230027)

用于磁流体热疗的磁流体多为超顺磁性,热涨落磁后效效应是其在交变磁场下产热的主要原因。文章以磁后效相关公式为基础,利用Shiliom is模型,对Fe3 O4磁流体耗散功率进行计算。理论分析结果表明:超顺磁性磁流体具有很高的产热效率,适合用于磁流体热疗;磁场的频率和强度与铁氧体微粒粒径对产热功率影响很大。

磁流体热疗;超顺磁性;磁后效;耗散功率

磁流体热疗是一种新型的癌症治疗方法,是目前医学研究的热点。磁流体热疗就是把磁流体注入肿瘤区域,然后置于交变磁场下加热至41～46℃之间并持续一段时间,利用癌细胞耐热性低于正常细胞的特性,达到杀死癌细胞而不损害正常细胞的目的。磁流体热疗是治疗癌症的一种新途径,它与传统的癌症治疗方法相比具有明显的优点[1]。目前,德国的Jordan课题组已经进入了人体试验阶段,并取得了较好的效果[2]。国内学者也正在研究这一课题,制造出了用于热疗实验的交变磁场装置,取得了一定的成果[3]。

研究磁流体热疗面临一个重要问题是如何在人体允许的磁场环境和较少磁流体剂量情况下,把病灶区域的温度均匀加热到热疗所需要的温度,并根据磁流体在交变磁场下的加热规律对其进行精确控制,使温度处于41～46℃之间。也就是说,在磁场强度较低且磁流体浓度较小的情况下,尽可能地提高产热效率。因此,研究超顺磁性磁流体在交变磁场下的产热规律对于磁流体热疗具有重要意义。

本文旨在对超顺磁性磁流体加热机制进行理论上的探究,通过理论分析和计算,对其产热机制和耗散功率计算进行了较为系统的阐述,且证明超顺磁性磁流体具有很高的产热效率,能达到热疗所需要的温度。

1 磁流体的超顺磁性

磁流体热疗所用的磁流体一般是由纳米级铁氧体(如Fe3O4)磁性微粒、表面活化剂(如油酸)以及基液组成。纳米铁氧体微粒主要是作为产热材料;表面活化剂则可以防止铁氧体微粒由于范德瓦尔斯力和磁相互作用发生凝聚,某些表面活化剂有利于特定癌细胞对磁流体微粒的吸附或吸收[4];基液一般是水,也可以是其它溶剂,主要作用是使得纳米磁微粒具有流动性,让包含表面活化剂的磁性微粒均匀弥散于基液中。

块状磁性材料在零磁场或弱磁场下,多处于多畴状态以降低静磁能。当磁性微粒的尺寸降低到一定程度,畴壁能大于颗粒退磁能时,整个颗粒成为一个单畴颗粒[5]。单畴微粒在任何外场作用下,都保持相同磁矩大小。单畴颗粒的尺寸减小到一个临界尺寸以下时,由于颗粒的热运动,在无外磁场情况下,磁矩方向不断地随时间改变。这样的颗粒组成的磁流体,呈现出一种所谓的“超顺磁性”,表现出和顺磁性物质类似的特性。此时,在零外磁场作用下,颗粒之间的相互作用可以忽略,颗粒磁矩方向随时间不断变化,总磁矩为零。在有外磁场作用情况下,表现出与外磁场方向一致的磁化现象,撤去外加磁场则磁化强度变为零,无剩磁,无矫顽力,朗之万定理对超顺磁性物质同样有效。

超顺磁性物质与顺磁性物质的唯一不同在于,超顺磁性微粒包含了超过105个原子,磁矩比顺磁性原子的磁矩大得多,因此磁化率也要大很多[6]。

超顺磁性临界尺寸的估算公式为:

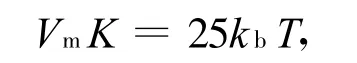
其中,V m为纳米微粒体积;K为磁各向异性常数;kb为玻尔兹曼常数;T为临界温度[7]。

磁流体热疗采用磁流体的微粒处于纳米级,在室温下,一般具有超顺磁性。

2 磁流体在交变磁场下的加热机制

用于磁流体热疗的交变磁场装置需要满足以下要求:

(1)热疗所采用的交变磁场装置频率一般在中低频(10～500 kH z),选择这一范围的原因是因为较低频率的交变磁场可能会刺激神经,容易在人体产生神经肌肉刺激症状,而较高的频率容易在人体内产生涡流加热,使得正常组织温度也升高[8]。

(2)医学上一般要求交变磁场强度幅值在30 kA/m以下,过高会产生涡流。磁场强度在空间上应尽量均匀,如果不均匀可能会引起加热不均,影响治疗效果。在磁流体热疗领域世界领先的德国Jordan课题组采用的交变磁场装置,其频率为 100 kH z,磁场强度幅值可变,最大为15 kA/m[9]。

综上所述,磁流体热疗所使用的磁场处于10～500 kH z之间,磁场强度幅值比较低,所以可以按低频弱场来讨论磁流体的加热机制问题。在低频弱场情形下,磁性材料主要有以下几种发热机制:磁滞效应、涡流效应、磁后效效应以及尺寸共振与磁力共振。

由于超顺磁性磁流体具有如下特性:无剩磁、矫顽力为零,微粒尺寸小,电阻很大,磁致伸缩效应小,这样,超顺磁性磁流体在交变磁场下主要产热机制是磁后效效应。磁后效又称磁黏滞,是指外磁场发生突变,材料的磁感应强度先是达到一个亚稳态,然后滞后地达到新的稳态,磁感应强度的变化落后于外磁场变化的现象,属于一种时间效应(弛豫过程)。对于纳米磁流体来说,主要存在2种弛豫机制:布朗(Brow nian)弛豫和尼尔(Neel)弛豫。布朗弛豫是微粒在液体内转动与液体分子碰撞引起的弛豫,尼尔弛豫是磁矩克服磁各项异性势垒引起的弛豫。实验证明,超顺磁流体在低频交变磁场下主要由热涨落引起的尼尔弛豫产热[10,11]。

在交变磁场下,单畴微粒由于体积很小,在外加磁场H=0 kA/m时的势垒(主要是磁各向异性)高度与k b T/2数量级相同,受到热涨落的影响,在外加交变磁场作用小于反转临界场的情况下,越过势垒反转到负方向。这样,磁化强度在热涨落的作用下,滞后地达到了新的稳态,这种弛豫机制是尼尔(Neel)先发现的。热疗中交变磁场下超顺磁性磁流体的损耗机制,实际上是一种热涨落的磁后效现象。在热涨落的“帮助”下,单畴微粒能越过各向异性势垒进行反转,超顺磁性磁流体不需要太大的外加磁场强度就可以达到很高的产热效率。

3 耗散功率计算

交变磁场下铁磁体的损耗公式同样适用于超顺磁流体[12],即

其中,f为交变磁场频率;H m为磁场强度;μ0为真空磁导率;μ″为磁化率的虚部。

布朗弛豫时间为:

其中,V H为超顺磁性微粒的体积;η为载液的黏度系数;kb为玻尔兹曼常数;T为温度。

尼尔弛豫时间为:

其中,K为磁各向异性常数;Vm为铁氧体微粒体积[13]。

有效弛豫时间为:

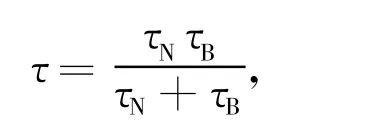
由于超顺磁流体在交变磁场下主要产热机制为尼尔弛豫,可以用单弛豫磁后效的相关公式进行计算。单弛豫磁后效计算公式[12]为:

此时,μ″达到峰值,取最大值,由(1)式可知,耗散功率与磁化率的虚部成正比,此时耗散功率最大。

由于主要的产热机制为尼尔弛豫,结合(5)式,由单弛豫时间磁后效耗散公式,单位体积磁性材料在交变磁场的损耗功率可转化为:

由(8)式、(9)式可知,除磁场的频率和强度以外,影响超顺磁性磁流体耗散功率的主要因素是铁氧体纳米磁性微粒的尺寸[15]。

现以文献[16]制备的Fe3O4磁流体作为计算对象:粒径d=8.6×10-9m,有效各项异性常数K eff=20.7×103J/m3,平均微粒磁矩 μm=290μB,c(Fe3O4)=0.07 mo l/L,Fe3O4的密度为ρ=5.18×10-3kg/m3,温度为 300 K 。

从上面的计算结果来看,对于磁流体热疗来说,SAR值太小,需采取一些改进。在ωτ≪1的情况下,耗散功率与H2m和 f2成正比。如果频率提高至500 kH z,磁场强度也提升至30 kA/m,耗散功率将提高约100倍,可达到约8×104W/m3,SAR值能达到5×104W/kg。

要达到更高的SAR值,可以适当地增大粒径。当 ωτ接近于 1时,通过(6)式进行估算,在500 kHz下,30 kA/m交变磁场下,粒径约为13 nm时,可以达到非常高的耗散功率,SAR值超过了1.5×106W/kg。经临界尺寸公式[7]估算,该尺寸的磁流体仍具超顺磁性。如果粒径过大,失去磁流体的超顺磁性,反而会降低耗散功率。

综上所述,耗散功率与磁流体的质量浓度、粒径大小、磁场频率和强度幅值相关。在磁场的强度幅值和频率不变的情况下,适当地增大粒径,能提高耗散功率,但是粒径过大,反而会使磁流体失去超顺磁性,在磁场强度较低的情况下会降低其耗散功率,因此存在一个产热功率最高的铁氧体微粒粒径。计算结果显示,超顺磁性磁流体在较低的磁场强度下,也有较高的产热效率,适合用于磁流体热疗。

4 结 论

通过计算发现,铁氧体微粒粒径对耗散功率的影响较大。对于相同材料的超顺磁性磁流体,除了磁场影响因素之外,主要与影响单畴微粒磁矩和尼尔弛豫时间的粒径相关,且在磁场频率和强度幅值不变的情况下,存在一个使得耗散功率最大的粒径。计算结果显示,超顺磁性磁流体具有很高的产热效率,适合用于磁流体热疗。因此,可以通过改变磁场频率、磁场强度、粒径等方式提高耗散功率和SAR值,从而达到磁流体热疗所需要的加热温度。

本文作者均为FDS团队成员,同时感谢FDS团队其它成员的支持。

[1] Jordan A,Scholz R,Wust P,et al.Magnetic fluid hyperthermia(MFH):cancer treatment w ith ACm agnetic field induced ex citation of biocom patiblesuperparamagnetic nanoparticles[J].Jou rnal of Mangetism and M agnetic Material,1999,201:413-419.

[2] Johan M,Gneveckow U,Jordan A,et al.Thermotherapy of prostate cancer using m agnetic[J].European U rology,2007,52(6):1653-1662.

[3] 吴 亚,孙剑飞,郭全忠,等.肿瘤热疗用交变磁场发生器的研制[J].东南大学学报:自然科学版,2004,34(6):794-796.

[4] Jordan A,Scholz R,Wust P,et al.Endocytosis of dextran and silancoated magnetite nanoparticles and the effect of intracellular hypertherm ia on human mamm ary carcinoma cells in vitro[J].Journal of Magnetism and M agneticM aterials,1999,194(1/3):185-196.

[5] 都有为.超细微粒的磁性[J].磁性材料及器件,1990,21(3):20-24.

[6] Bean C P,Livingston JD.Superparamagnetism[J].Jou rnal of Applied Physics,1959,30(4):S120-S129.

[7] 张立德.超微粉体制备与应用技术[M].北京:中国石化出版社,2001:41-51.

[8] 郭中华.交变磁场加热治疗肿瘤测控技术的研究进展[J].中国医疗器材杂志,2006,30(1):39-42.

[9] Johannsen M,Jordan A,Scholz R,et al.Evaluation of magnetic fluid hypertherm ia in a standard ratmodel of prostate cancer[J].Journal of Endou rology,2004,18(5):495-500.

[10] Rovers SA,H oogenboom R,Kemmere M F,et al.Relaxation processes of superparamagnetic iron oxide nanoparticles in liquid and incorprated in poly(methylmethacry late)[J].JPhy sChem C,2008,112(40):15643-15646.

[11] 王煦漫,古宏晨,杨正强,等.磁热疗用Fe3O4在交变磁场中的热效应[J].上海交通大学学报,2005,39(2):275-278.

[12] 戴道生,钱昆明.铁磁学:下册[M].北京:科学出版社,1987:1-89.

[13] Rosensw eig R E.Heating magnetic fluid w ith alternating m agnetic field[J].Jou rnal of Magnetism and Magnetic Materials,2002,252(1/3):370-374.

[14] Shliom is M.M agnetic fluids[J].Soviet Physics Uspekhi,1974,17(2):153-169.

[15] Jordan A,Rheinlander T,Scholz R,et al.In crease of the specific absorption rate(SAR)by magnetic fractionation of m agnetic fluids[J].Journal of Nanoparticle Research,2003,5(5/6):597-600.

[16] Lim a E,Brandl A L,A relaro A D,et al.Spin diso rder and m agnetic anisotropy in Fe3O4nanoparticles[J].Journal of A pplied Physics,2006,99(8):083908.

Power dissipation of superparamagnetic fluid in magnetic fluid hypertherm ia

XIA Dan1, HE Xiao-xiong1, CHEN Hong-li2,3

(1.School of Electronic Science and Applied Physics,H efei University of Technology,H efei 230009,China;2.Institute of Plasma Physics,Chinese Academy of Scien ces,H efei 230031,China;3.School of Nuclear Science and Technology,University of Science and Technology of China,H efei 230027,China)

Magnetic fluid used for hypertherm ia is mostly superparamagnetic.Magnetic aftereffect by thermal fluctuation is them ain reason for the heat production in alternatingm agnetic field.In view of the related formulasofm agnetic aftereffect,the Shiliomismodel is used to calculate power dissipation of the Fe3O4m agnetic fluid.Theoretical analysis show that the superparamagnetic fluid has high heat efficiency,which is suitable for themagnetic fluid hypertherm ia.The frequency and intensity ofmagnetic field and the size of ferrite particles have a great impact on the production of thermal pow er.

magnetic fluid hyperthermia;superparamagnetism;m agnetic aftereffect;power dissipation

O 441.6

A

1003-5060(2011)01-0058-04

10.3969/j.issn.1003-5060.2011.01.014

2009-12-14;

2010-12-30

安徽省自然科学基金资助项目(070413085);安徽省高校自然科学研究重点资助项目(KJ2009A 091)

夏 丹(1986-),男,湖南桃江人,合肥工业大学硕士生;

何晓雄(1956-),男,安徽宿松人,合肥工业大学教授,博士生导师;

陈红丽(1968-),女,安徽淮北人,博士,中国科学技术大学教授,硕士生导师.

(责任编辑 张秋娟)