基于波动方程的AVO模型数值模拟方法研究
吕姗姗,熊晓军,贺振华
(1.成都理工大学“油气藏地质及开发工程”国家重点实验室;2.成都理工大学地球物理学院)
0 引言
自Ostrander[1]采用反射系数随入射角的变化特征定性地识别“亮点”型含气砂岩以来,AVO技术目前已被广泛应用于油气储层的预测[2]。近年来,国内外许多学者对于AVO技术的研究主要集中在AVO 反演方面[3],即基于地震、测井、钻井等资料来反演各种AVO属性[4](如纵、横波速度反射率及反射系数等)并用于油气预测,但往往得不到理想效果,原因是忽略了AVO模型正演(数值模拟)的研究,即忽略了目的层是否存在明显的AVO异常特征的问题。在关于AVO模型数值模拟的研究方面,目前主要集中在提高反射(或透射)系数的计算精度和计算效率方面,即对常规的基于Zoeppritz方程[5]的方法进行改进[6-9]。这些研究成果对于研究单界面的AVO特征是有效的,但是对于实际的地层模型而言,地下某个深度的反射是上下相邻多个反射点综合作用的结果,所以还必须考虑由反射系数计算合成地震记录的问题。
常规的AVO模型数值模拟采用的是褶积方法,即将给定的地震子波与不同入射角的反射系数进行褶积,得到的合成地震记录具有计算简单、快速的优点,缺点是很难准确地设定地震子波参数(如子波类型、主频、延续度等)。如果子波参数选取不当,得到的模拟记录会与实际地震记录存在较大差异,从而得到错误的AVO特征,将直接影响后续AVO反演工作。
为有效提高AVO模型数值模拟的精度,笔者从地震数值模拟的角度出发,采用频率-波数域的声学波动方程代替褶积进行AVO模型数值模拟计算[10],其模拟记录的波场信息丰富,不仅包含了地震波的运动学特征和动力学特征[11],而且可通过采用点脉冲作为初始震源子波来模拟其在地下介质中的传播波场,从而获得与实际地震记录基本一致的模拟记录。
1 方法原理
1.1 Zoeppritz方程
根据弹性波波动理论,当地震波在传播过程中遇到弹性分界面时,将发生反射和透射,同时还会发生波形转换和能量的重新分配,即在弹性分界面上一个波变成多个波,如图1所示。
从图1可以看出,P1波到达弹性界面x时转换成反射P1P1波与P1S1波以及透射P1P2波与P1S2波,其能量的重新分配可以通过Zoeppritz方程进行表征,即

式中:α1和α2分别表示纵波的入射角(同反射角)、横波的反射角,β1和β2分别表示纵波和横波的透射角;vP1,vS1,ρ1分别为界面上层介质的纵、横波速度和密度,vP2,vS2,ρ2分别为界面下层介质的纵、横波速度和密度;RPP,RPS,TPP,TPS分别表示纵、横波反射系数和纵、横波透射系数。

图1 入射P波位移矢量图Fig.1 The displacement vector of incident P-wave
式(1)表示了反射纵波、反射横波、透射纵波和透射横波之间的能量分配关系,对于单个反射界面模型而言,如果已知地层模型(物性参数)及入射角,便可根据式(1)计算该反射界面上地震波的反射或透射系数。
1.2 频率-波数域波动方程数值模拟方法
利用波动方程进行地震波场数值模拟的核心是波场延拓。对于垂向变速介质,利用二维标量波动方程在频率-波数域可以得到各个深度间隔内的相位移延拓的正演和偏移公式[12]
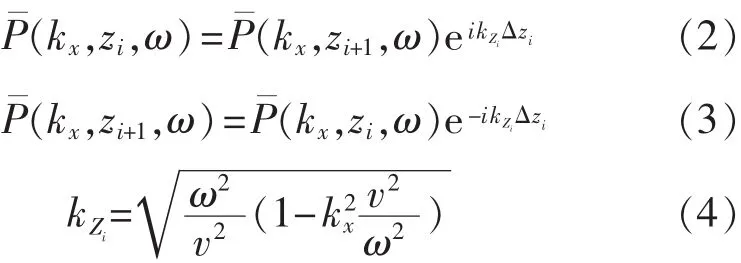
式中:kx表示x方向的波数;kZi表示深度间隔i内在z方向的波数;ω表示频率;Δz表示当前深度延拓的深度间隔。其中,式(2)为二维正演延拓公式,其延拓方向为由下至上延拓,式(3)为二维偏移延拓公式,其延拓方向为由地面向下延拓。
利用式(2)和式(3)进行波场延拓的假设条件是:在深度延拓间隔内地层的横向速度不变化,即横向为均匀介质。对AVO模型数值模拟而言,往往针对的是单井资料的数值模拟,即一维模型的数值模拟问题。为了利用式(2)进行波场延拓计算,笔者将一维模型外推至二维水平层状模型(模型的每个单道数据都与原始的一维模型一致),从而满足了相移法延拓的假设条件。相对于其他的波场延拓算法(如相位移加插值方法、分步傅里叶方法、广义屏方法)而言,相移法是计算效率最高且最准确(仅对于水平地层而言)的方法。
1.3 计算步骤
基于上述方法理论,笔者提出的基于波动方程的AVO模型数值模拟的计算步骤如下:
(1)构制一个地质模型,从钻井、测井以及岩石物理实验分析得到纵、横波速度和密度以及地层厚度等参数,通过Zoeppritz方程[式(1)]求出不同角度的反射系数。
(2)提取0°反射系数曲线,假定速度横向不变,并将其外推为二维的水平层状速度模型和反射系数模型(初始震源子波)。
(3)采用波动方程[式(2)]进行地震波场延拓与成像数值模拟。
(4)抽取中间道记录作为0°入射角的AVO模拟记录。
(5)提取1°反射系数曲线,重复以上步骤(2)~(4),每次加上1°的增量,直至提取到30°反射系数曲线,最后得到角道集。
2 实际资料试算
为了验证文中提出的基于波动方程的AVO模型数值模拟方法的有效性,笔者采用四川某区的碳酸盐岩鲕滩气藏进行了实例计算。图2所示的是该区L06井AVO计算实例,该井在5 953 m处钻遇气藏(对应图中的GAS_top层位段至GAS_bot层位段),其过井地震反射为强反射特征。图2(a)左起第1列为实际过井地震剖面,第2列为提取的过井地震道,第3列为将地震解释层位与井分层对齐后采用常规褶积法得到的合成地震记录。可以看出,合成记录与过井地震道在深度5 700~6 050 m处的相似度较差。图2(b)是采用本文提出的新方法得到的AVO模拟记录,其中的0°记录(左边第1道)对应叠后模拟记录,该图中5 950 m与6 000 m指示线所示的地震波形特征与图2(a)中的过井地震道相似度较高,如5 950 m处显示为强振幅,与实际地震道的强振幅相符,证明了新方法的有效性。在5 800 m蓝线所示处,波动方程AVO模拟记录的振幅特征虽与实际地震振幅特征存在一定的差别,但与褶积法相比,仍显示出较好的模拟效果。
提取图2中气层底界面处的AVO反射振幅曲线,得到与该图红色箭头处相对应的振幅变化曲线(图3)。由图3可以看出,该气层的AVO响应特征为:随着入射角度的增加,反射振幅值增加,呈现第3 类 AVO 反射特征[13]。
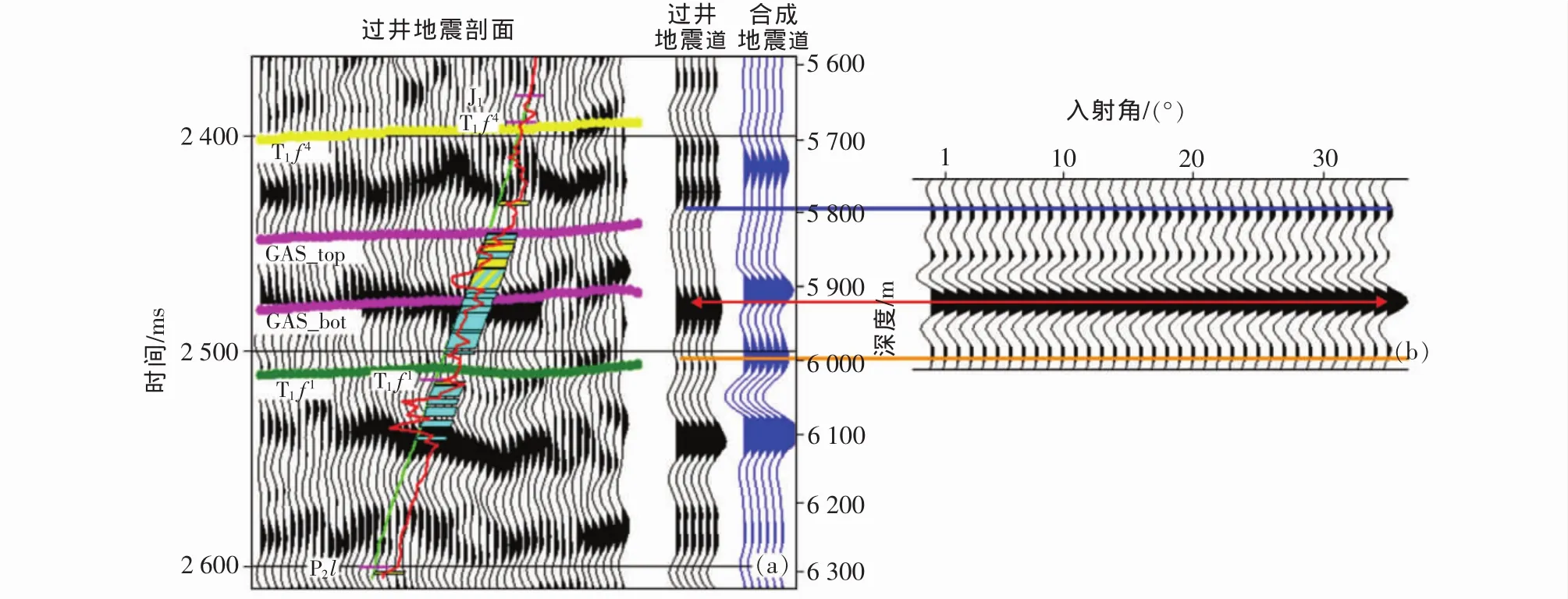
图2 四川某区L06井AVO计算实例Fig.2 The AVO calculation example for L06 well in some zone of Sichuan

图3 与图2红色箭头处相对应的振幅变化曲线Fig.3 The amplitude curve corresponding to the red line in Fig.2
3 结论
基于波动方程的AVO模型数值模拟有效地克服了基于褶积法AVO模型数值模拟中存在的子波参数设定带来的精度问题,虽然其计算量较大,但可以得到与地下实际情况基本一致的地震反射记录,且计算精度较高。
[1]Ostrander W J.Plane-wave reflection coefficients for gas sands at nonnormal angles of incidence[J].Geophysics,1984,49(10):1 637-1 648.
[2]王大兴,于波,张盟勃,等.地震叠前分析技术在子洲气田的研究与应用[J].岩性油气藏,2008,20(1):95-100.
[3]李艳玲.AVO叠前反演技术研究[J].大庆石油地质与开发,2006,25(5):103-106.
[4]梁劲,梁金强,王宏斌,等.AVO属性分析在天然气水合物地震解释中的应用[J].物探化探计算技术,2008,30(1):22-27.
[5]Zoeppritz K,Erdbebenwellen VIIIB.On the reflection and propagation of seismic waves[J].Gottinger Nachrichten,1919,1:66-84.
[6]Richards P G,Frasier C W.Scattering of elastic waves from depthdependent inhomogeneities[J].Geohysics,1976,41(3):441-458.
[7]Shuey R T.A simplification of the Zoeppritz equations[J].Geophysics,1985,50(4):609-614.
[8]Gray D,Goodway B,Chen Taiwen.B ridging the gap:using AVO to detect changes in fundamental elastic constants[J].SEG Expanded Abstracts,1999,18:852-855.
[9]杨绍国,周熙襄.Zoeppritz方程的级数表达式及近似[J].石油地球物理勘探,1994,29(4):399-412.
[10]刘定进,印兴耀,陆树勤,等.波动方程保幅叠前深度偏移与AVO响应[J].中国石油大学学报:自然科学版,2009,33(4):45-51.
[11]边立恩,贺振华,黄德济.饱含流体介质的地震波场特征及频率分布[J].岩性油气藏,2008,20(3):74-78.
[12]贺振华.反射地震资料偏移处理与反演方法[M].重庆:重庆大学出版社,1989:56-57.
[13]王浩,罗兵,李霆.弹性阻抗对比分析[J].岩性油气藏,2010,22(3):110-113.

