全程跟踪卫星或飞船的测控站数量模型
王积建,王晓红
(浙江工贸职业技术学院 a.基础部;b.图书馆,浙江 温州 325003)
全程跟踪卫星或飞船的测控站数量模型
王积建a,王晓红b
(浙江工贸职业技术学院 a.基础部;b.图书馆,浙江 温州 325003)
为了确定全程跟踪卫星或飞船的测控站数量,在不考虑地球自转影响和考虑地球自转影响的情况下,使用几何方法分别建立了对卫星或飞船进行全程测控时所需要的最少测控站数量模型,并针对“神舟七号”飞船给出了所需最少测控站数量,估算出“神舟七号”飞船所能测控的有效范围。
卫星测控;数学建模;神舟飞船
0 引 言
近年来,神舟系列飞船的成功发射显示了我国在航天领域取得的巨大成就,航天也成了人们普遍关注的热门话题。2009年全国大学生数学建模C题就是关于卫星或飞船的跟踪测控问题,给出以下三个问题:
(1)在所有测控站都与卫星或飞船的运行轨道共面的情况下至少应该建立多少个测控站才能对其进行全程跟踪测控?
(2)如果一个卫星或飞船的运行轨道与地球赤道平面有固定的夹角,且在离地面高度为H的球面S上运行。考虑到地球自转时该卫星或飞船在运行过程中相继两圈的经度有一些差异,至少应该建立多少个测控站才能对该卫星或飞船可能飞行的区域全部覆盖以达到全程跟踪测控的目的?
(3)收集我国一个卫星或飞船的运行资料和发射时测控站的分布信息,分析这些测控站对该卫星所能测控的范围。文献[1]只是给出了一个解决以上三个问题的基本思路,但缺乏完整性和可读性。本文在此基础上进行深入、详细的研究,完整地解决了卫星或飞船的全程跟踪测控问题。
1 问题1的解决
1.1 当卫星运行轨道为圆时
卫星运行轨道为圆时的剖面如图1所示。其中,设R为地球半径;H为卫星距离地面的高度;为卫星观测站的最低仰角;v为卫星的线速度。
在图1所示的三角形ODS中,利用正弦定理得:
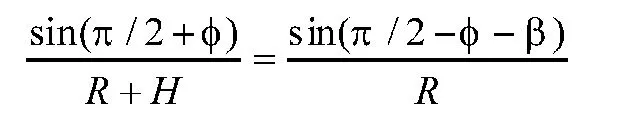

图1 卫星运行轨道为圆时的剖面
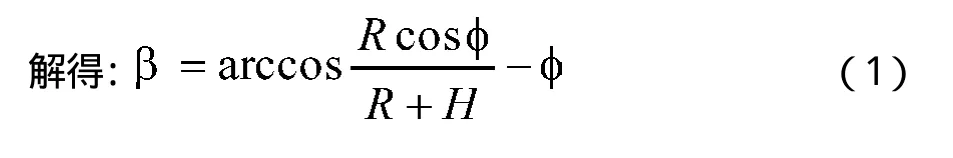
其中[]内取整数部分。
这表明卫星到地球表面的距离越大,一个测控站的观测范围越大,所需测控站的数目越少。

表1 卫星或飞船在不同高度下所需测控站数量
每个测控站所能测控的时间为:

对于“神舟七号”飞船,H=343km,所需测控站数量为n=[11.5177]+1=12个。由v=7.820km/s可得出每个测控站所能测控的时间为t=3.61m i n。
1.2 当卫星运行轨道为椭圆时

以地球中心为极点O,卫星运行轨道(椭圆)的左焦点F1在极点,射线F1F2为极轴,卫星运行轨道为椭圆时的剖面如图2所示。
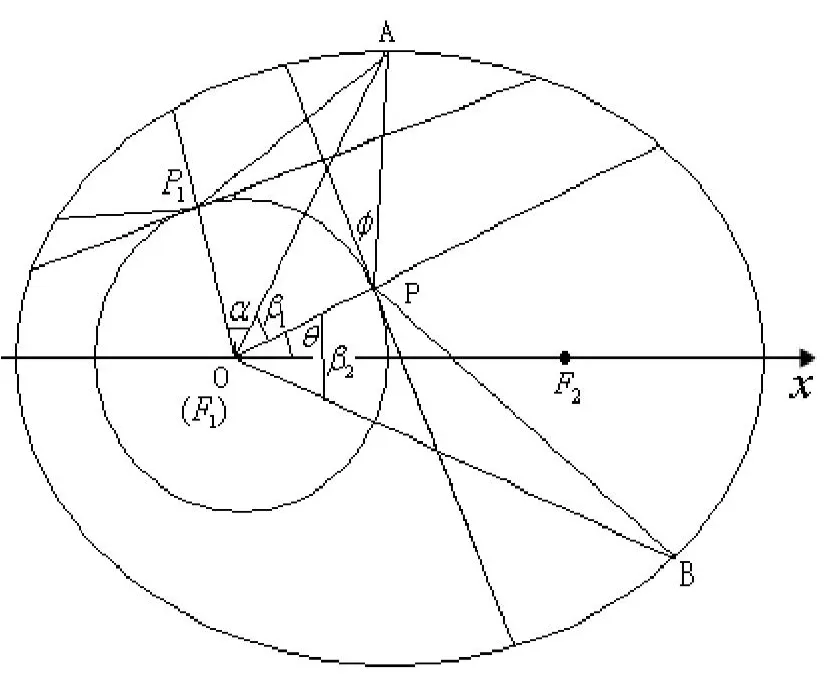
图2 卫星运行轨道为椭圆时的剖面


在图2所示的三角形OAP1中,利用正弦定理得:

逐步递推求解,直到 为止,此时确定的最后一个测控站为Pn。这样一共有n+1个测控站。
由(4)、(5)、(6)式可求出近地点d1和远地点d2在不同组合下所需测控站数量(见表2)。

表2 椭圆轨道下所需测控站数量
以“神州七号”飞船为例,其近地点为200 km,远地点为343 km,通过计算得出需要14个测控站就可实现全程测控的目的。“神州七号”飞船14个测控站的坐标(第一个测控站取)见表3。
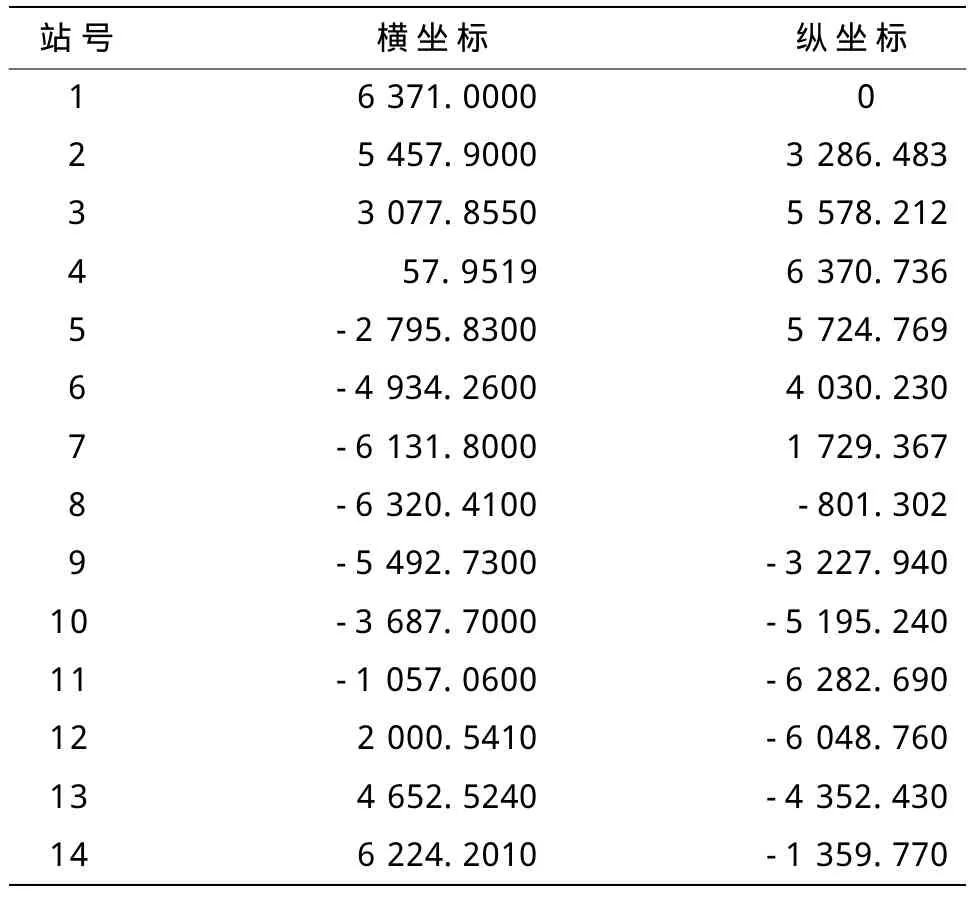
表3 “神州七号”飞船14个测控站的坐标
画出14个测控站点、地球表面曲线、飞船轨迹及每个测控站测控的范围,如图3所示。实线是地球表面曲线,五角星表示测控站,虚线表示飞船轨迹,圆点表示各个测控站测控的始点和终点,从每个测控站点出发的折线表示该测控站测控的范围。
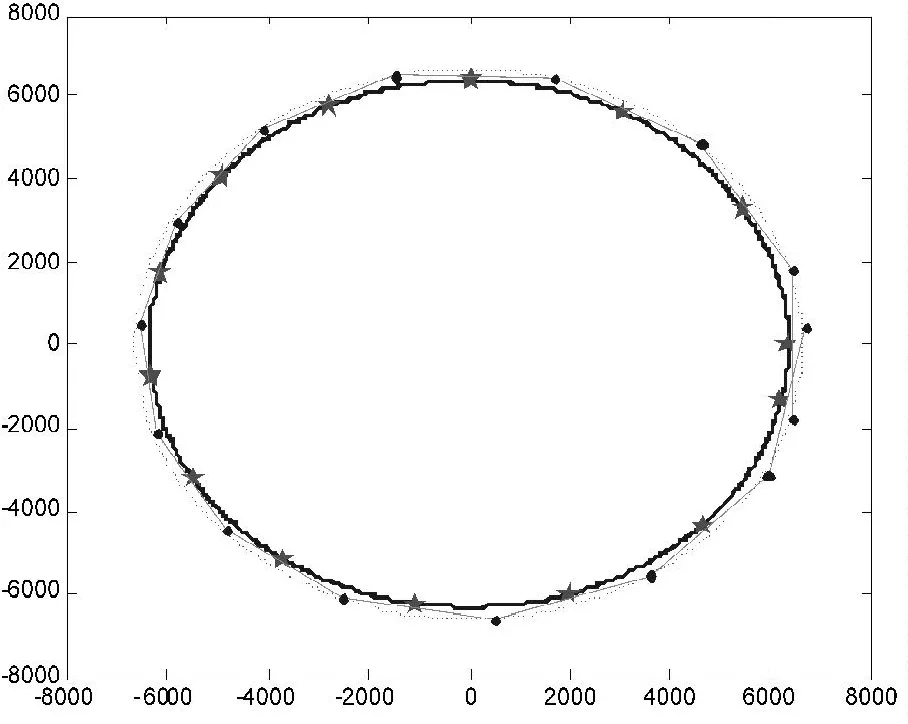
图3 “神州七号”飞船14个测控站的分布
以下推导各个测控站所能测控的时间范围。
该测控站所能测控的时间为:

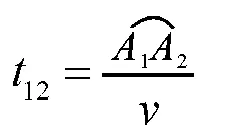
以“神州七号”飞船为例,通过计算得出14个测控站所能测控的时间(见表4)。
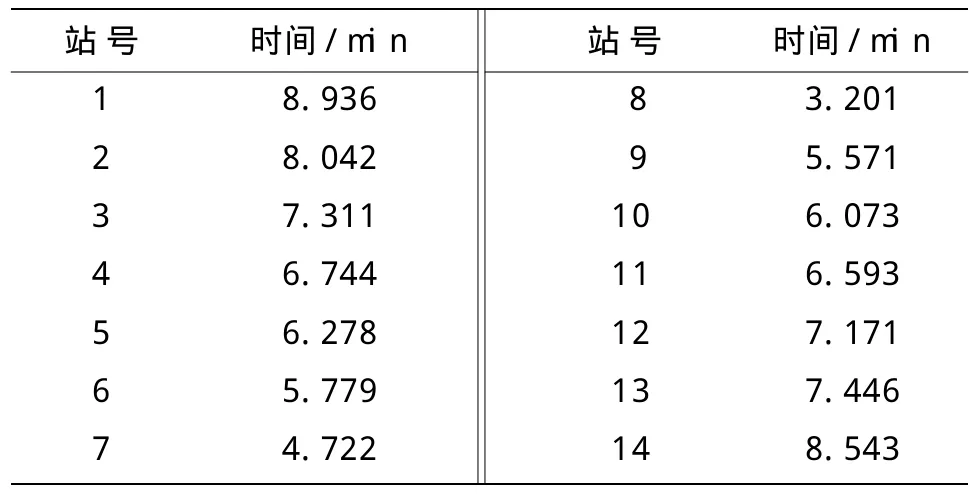
表4 “神州七号”飞船14个测控站所能测控的时间
2 问题2的解决
由于地球自转的影响,飞船在运行过程中的每一圈的星下线的位置都会向西偏移,如图4所示[2]。

图4 “神州七号”飞船星下线轨迹
任何一个地面上固定的测控站都无法观测飞船的某些圈的运行轨道段。根据飞船运行轨道与地球赤道平面有固定夹角这一情况,假设飞船在离地面高度为H的球面S上运行,此时飞船的运行区域落在一个赤道周围的球面的带形区域中。考虑到地球自转时该飞船在运行过程中的相继两圈的经度有一些差异,希望通过一些测控站覆盖区域以达到全程跟踪监测的目的。这需要计算所需覆盖的面积和一个测控站所能覆盖的区域面积,然后再计算这二者的比值。
2.1 一个测控站所能覆盖的区域面积
由于地面一个测控站的测控范围只考虑其与地平面夹角3°以上的空域,所以该测控站的测控范围形成一个以测控站为顶点的圆锥体,如图5所示。


图5 以测控站为顶点的圆锥体
2.2 飞船形成的球形带状区域面积
飞船运行的区域是球面上不包括南北两极所在的球冠的带状区域,如图6所示。
图6 飞船形成的球形带状区域

2.3 计算测控站所需数量
覆盖飞船运行区域测控站所需数量为:
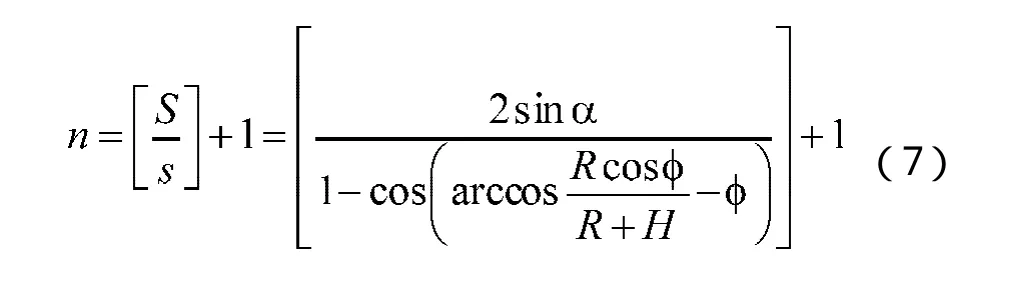
上面的计算只是一个非常粗略的估计,实际上每个测控站的测控区域免不了有些重合。可使用圆内接正六边形覆盖所涉及的区域,如图7所示。
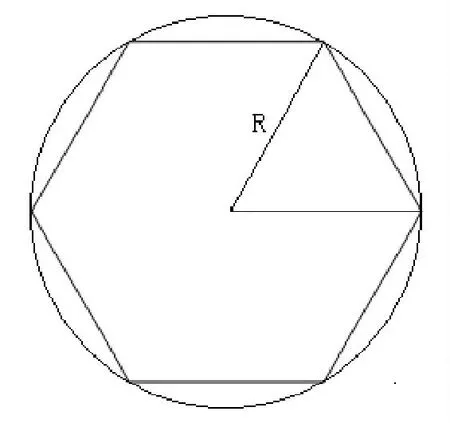
图7 圆内接正六边形区域

3 问题3的解决
“神舟七号”飞船在第583 s飞船与火箭分离,随后飞船正常进入预定轨道,飞船在近地点200 km、远地点343 km的椭圆轨道,入轨飞行速度7.820 km/s。实施变轨后,在距地球表面约343 km的近圆工作轨道运行,飞行一圈需要90 m i n[3]。“神舟七号”飞船测控通信系统,除了5艘远望号测量船外,在国内有主场站、喀什站、和田站、东风站、青岛站、渭南站、厦门站7个地面测控站;在国外也有卡拉奇站、马林迪站、圣地亚哥站、纳米比亚站4个地面测控站;还有远一站等5个测控站,以上16个测控站组成了一个“神舟七号”飞船的监控天网,时刻掌握着相关信息,并发送指令,全程保护安全[4]。“神舟七号”飞船16个测控站的经纬度见表5。
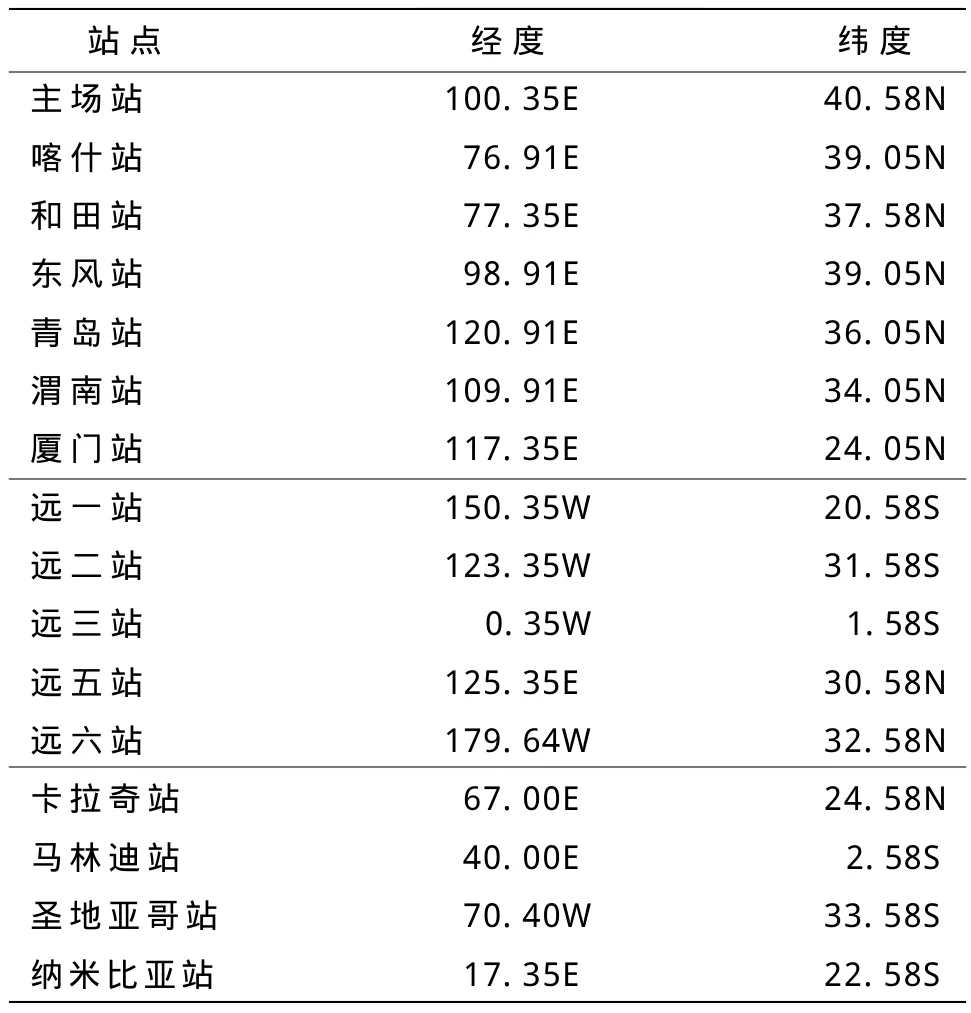
表5 “神舟七号”飞船16个测控站的经纬度
使用O r b i t r o n软件,在(局部)世界地图上动态描绘出“神舟七号”飞船的星下线轨迹,并根据各个测控站的经纬度利用网格法求测控覆盖率,如图8所示。需要说明的是,飞船运行区域的投影网格的长度是从西经180°到东经180°,宽度是从南纬42.2°到北纬42.2°。
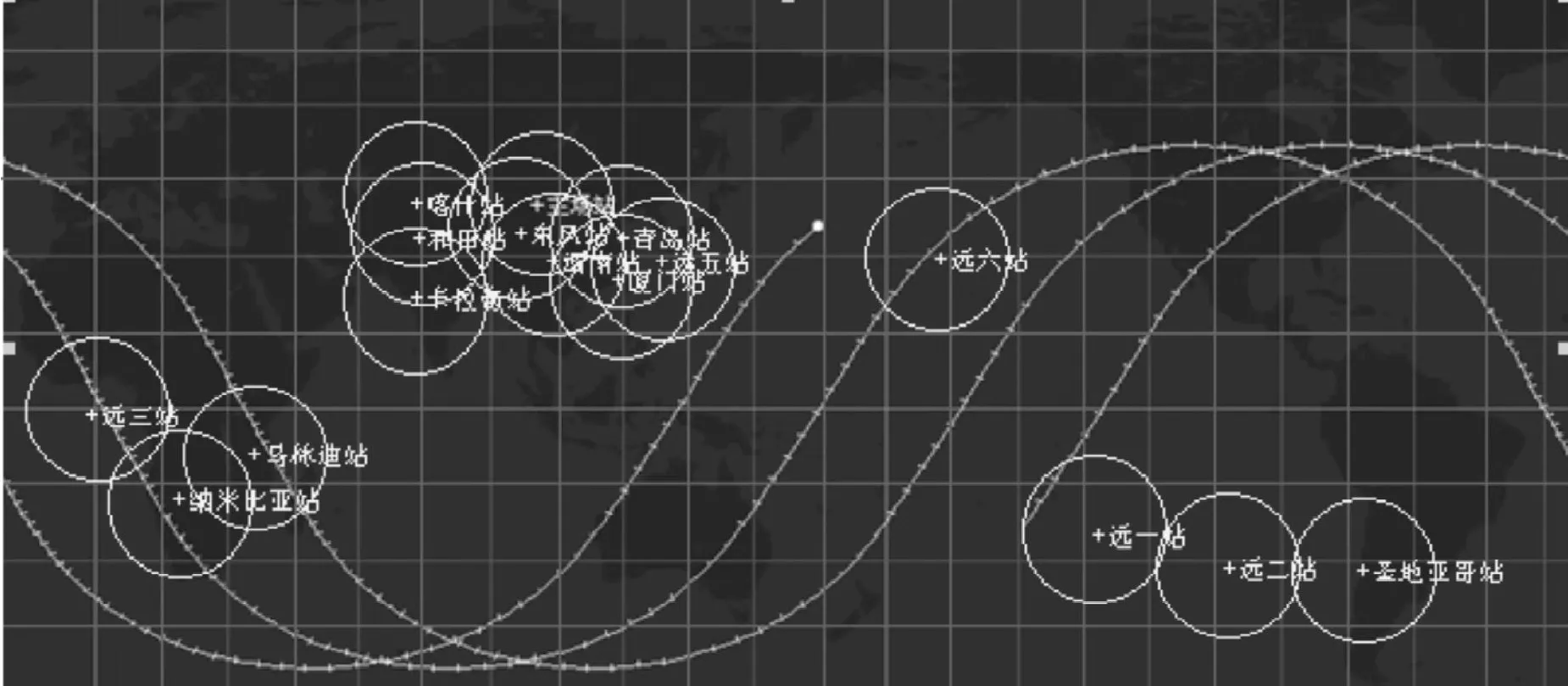
图8 网格法求测控覆盖率
利用网格法可估算“神舟七号”飞船的测控覆盖率[5]。将飞船运行的球形带状区域面积在地球表面上的投影展开成网格平面,画出每个测控站所能测控的范围(用圆面积表示),通过计算所有测控站所能测控的有效面积之和与飞船运行的区域面积的比值,就是测控覆盖率。
“神舟七号”飞船轨道剖面如图9所示。
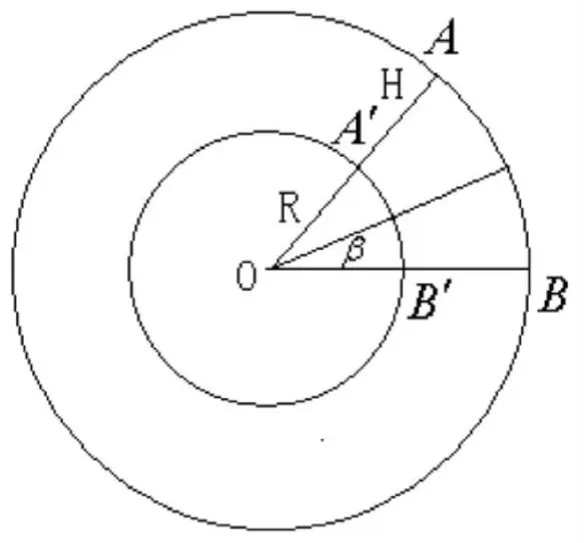
图9 “神舟七号”飞船轨道剖面


4 结束语
使用几何方法建立了对卫星或飞船进行全程测控时所需最少测控站数量模型,并针对“神舟七号”飞船给出了所需最少测控站数量,估算出“神舟七号”飞船所能测控的有效范围。因此,具有思路清晰、方法简捷、模型简单、结果准确的优点,尤其适合高职学生的知识基础和能力水平。
[1] 周义仓,谭永基. 卫星和飞船的跟踪测控问题的命题和评注[ J ] .工程数学学报,2009,26 (增刊二) :189-195.
[2] 查春明.神舟七号载人飞船运行轨迹图[EB/OL].(2008-09-26)[2011-01-18].http://news.qq.com/a/20080926/002700.htm.
[3] 神七飞行任务计划曝光:27 日下午6 时左右出舱[EB/OL].(2008-09-23)[2011-01-18].http://www.chinanews.com/gn/news/2008/09-23/1390490.shtml.
[4]5 艘巨轮加11 个地面站组成测控天网护神七[EB/OL].(2008-09-26)[2011-01-18].http://news.sohu.com/20080926/n259755655.shtml.
[5] 钟志平,郑思颖,罗凯. 航天测控网的数学模型[ J ] .工程数学学报,2009,26 (增刊二):177-178.
Quantitative Model on Monitoring and Control Stations of Traching Satellites or Spaceships
WANG Jijiana, WANG Xiaohongb(a. Basic Courses Department;b. Library, Zhejiang Industry and Trade Polytechnic, Wenzhou,325003, China)
To determine the number of on monitoring and control stations of tracking satellites or spaceships, in both the case of disregarding and regarding the influence of the rotation of the earth, a quantitative model of the fewest on monitoring and control stations of tracking satellites or spaceships by geometric methods is established. In addition, in view of "Shenzhou VII" manned spaceship, the fewest monitoring and control stations needed is presented and the effective range "Shenzhou VII" manned spaceship can cover is estimated.
Satellite monitoring and control; Mathematical modeling; Shenzhou VII manned spaceship
V556
A
1671-4326(2011)02-0042-06
2011-02-24
王积建(1966—),男,甘肃景泰人,浙江工贸职业技术学院基础部副教授,硕士;王晓红(1965—),女,辽宁辽阳人,浙江工贸职业技术学院图书馆馆员.
王玮明]

