基于前景理论的区间数多准则决策方法

胡军华，许 琦

（中南大学 商学院，湖南 长沙 410083）

基于前景理论的区间数多准则决策方法

胡军华，许 琦

（中南大学 商学院，湖南 长沙 410083）

针对准则偏好值为区间数的不确定性决策问题，提出了一种基于前景理论的多准则决策方法。该方法将准则值看作给定区间内N个等差随机数，利用正态分布的分布函数来表示区间内准则值的分布规律，在给定各准则参考点的基础上，通过价值函数和决策权重函数计算方案在各准则下的前景值，并通过加权平均得到各方案的总前景值；根据前景值的大小对所有方案排序并得到最优方案。该方案的可行性通过一个简单实例得到了论证。

多准则决策；区间数；前景理论；正态分布

一、引 言

多准则决策（Multiple Criteria Decision Making，简称MCDM）是从有限个备选方案集中经过综合权衡各个准则（或指标）后，对方案集排序并选出最满意方案。它是决策理论与方法研究中十分重要的内容，具有广泛的应用背景。由于客观世界的复杂性和人们主观决策的不确定性，经常会导致决策信息的不确定性和不完备性，所以在实际的多准则决策问题中，决策者对于某些准则的评价很难赋予一个确定的数值，很多情况下只能给出它的一个取值范围，这使得准则值通常是以区间数的形式出现的。目前一些文献研究了准则值变量在区间内的分布规律，如均匀分布和正态分布，其中周光明和刘树人利用区间数服从均匀分布解决区间数的排序问题［1］，张全、樊治平、潘德惠给出两区间数比较的可能度公式，即研究了准则值在评价区间内服从正态分布的多准则决策问题［2］。

基于区间数的多准则决策问题实际上是不确定条件下的决策问题，对于不确定条件下的决策问题，很多学者提出了各种不同的理论，其中最有影响的是Von Neumann和Morgenstern于1944年提出的期望效用理论（Expected Utility Theory，EUT）［3］178－181。该理论的一个核心理论基础就是假定所有的决策者都是“完全理性人”，认为在备选方案既定的情况下，若以效用来描述各备选方案的吸引程度的话，决策者会选择期望效用最高的备选方案，即期望效用最大化。但实际上人并不是纯粹的理性人，决策还受到人的复杂的心理机制的影响。因此，期望效用理论对人的风险决策的描述性效度一直受到怀疑。Kahneman和Tversky通过调查和试验，搜集了许多个体行为的研究成果，发现人们在不确定条件下的判断与决策行为常常会系统地偏离传统理性假设，而这些偏差具有一定的规律性。于是在1979年提出了前景理论（Prospect Theory，PT）［4］，后来发展成为累积前景理论（Cumulative Prospect Theory，CPT）［5］，其对不确定条件下的决策具有很好的解释力。

Kahneman和Tversky提出的前景理论为判断和决策的跨科学研究做出了开创性的贡献，主要应用于经济学（尤其是行为经济学）、管理学、金融投资学等领域。例如，孙伟等以前景理论为基础研究了行为决策下的证券市场异象［6］，张波涛等基于前景理论研究了资本结构决策中财务保守行为的重要原因［7］，David等尝试用前景理论解释了股票回报对分析者预测行为的影响［8］。前景理论在其他领域也有一些应用研究，如王正武等利用前景理论建立了不确定条件下出行者的多目标选择模型［9］，Goda和Hong研究了累积前景理论在地震设计中的参数默认设置问题［10］。不过，这些应用研究基本上局限于单准则决策问题中的应用，而对于基于前景理论的多准则决策问题研究还较少，如Zank等研究了基于累积前景理论的多属性效用理论［11－13］，胡军华等利用前景理论对以语言评价为准则值的多准则问题进行了研究［14］。

本文研究准则偏好为区间数的多准则决策问题，通过构造一个服从正态分布的区间数概率分布函数，在前景理论的基础上，提出了一种基于区间数和前景理论的多准则决策方法。

二、前景理论

前景（Prospect）表示不确定事件。S＝ ｛1，…，n｝，其中n≥3表示自然状态有限集，自然状态si∈S；X代表可能结果有限集，可能结果x i∈X。在自然状态集S和可能结果集X之间存在着函数f，每个自然状态si∈S对应可能结果集X中的一个结果x i，表达如下：f∶S→X，这里f代表不确定前景，将自然状态集S的子集A i称为事件（Event），事件Ai发生时会产生结果x i，x i＞x j当且仅当i＞j。各种可能前景结果x i按递增顺序排列，即x1≤x2≤…≤x h≤x h＋1≤…≤x n，其中前景结果依赖参考点x h的取值，当x h＝0时，表示中性状态，x h＞0时表示获得，x h＜0时表示失去。

前景的整体价值是由可能结果的价值函数v和不确定事件的累积概率权重函数（或称决策权重函数）π决定的。整体价值函数用大写V表示如下：

Tversky和Kahneman给出了价值函数v的一种形式［5］。因为这种形式的价值函数能很好满足决策者在面临收益时趋向风险规避和面临损失时趋向于风险追求的偏好特性，所以它得到了广泛的应用，其具体表达式是：

其中x是表面价值的得失，得为正，失为负；α和β为风险态度系数，0＜α＜1，0＜β＜1，α和β越大表明决策者越倾向于冒险，α＝β＝1时，决策者被视为风险中立者；λ为损失规避系数，若λ＞1，则决策者对损失更加敏感；v为决策价值，很明显，v（0）＝0。

累积前景理论（Cumulative Prospect Theory，CPT）的决策权重函数采取累积形式，并且采取不同的决策权重对待损失和盈利。把不确定权重转换为概率形式，Tversky和Kahneman定义的获得和失去的决策权重分别为［5］：

其中x h为参考点，w＋和w－分别是获得和失去的决策权重函数，π＋n＝w＋（p n），π－1＝w－（p1）。针对风险前景为两个或两个以上结果的情况，Prelec D.给出的w＋和w－函数分别是［15］67－92：

其中γ＋，γ－和φ是模型的参数，γ＋＞0，γ－＞0，φ＞0。

三、区间数的概率函数及区间数多准则决策问题描述

（一）区间数的概率函数

定义1 设R为实数域，称珘a＝［a L，aU］＝｛a｜a L≤a≤aU，a L，aU，a∈R｝为闭区间数。若0＜a L≤aU，则称珘a＝［a L，aU］为正闭区间数。若a L＝a U，该区间数退化为普通的实数［16］。

（二）区间数多准则决策问题的描述

（三）区间数的处理

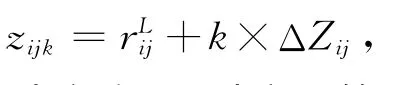
四、基于前景理论的多准则决策方法

基于前景理论进行的多准则决策步骤如下：

步骤2 将区间数转化为N个离散数据集，计算出各方案的离散准则值zijk。

步骤3 选定各准则的参考点，zj0表示准则Aj的参考点，j∈ ｛1，2，…，n｝；根据方案在准则中的取值及参考点，计算各方案在各准则下的结果。依据前景理论，可能存在的获得和损失结果集为X，x ijk∈X表示可能的收益或者损失。x ijk＝zijk－zj0，zijk∈Zij，0＜k＜N。

步骤4 根据式（7）计算出矩阵珟A各准则值所对应的概率值。

步骤5 方案Di在准则a j下的前景值

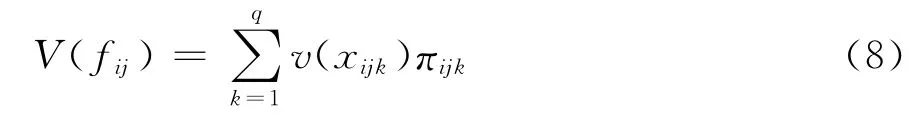
其中，根据式（2）得到价值函数

再根据式（3）～（6）得到决策权重函数

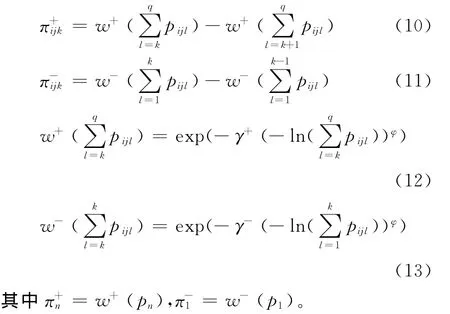
根据式（8）～（13），计算各方案在各准则下的前景值。V（f ij）表示方案Di在准则A j下前景值，i∈ ｛1，2，…，m｝，j∈ ｛1，2，…，n｝。

步骤7 根据前景值对各方案进行排序，选择前景值最大的方案为最优方案。

五、算例分析

有3个基础设施建设项目，分别为方案D1、方案D2和方案D3。现在对这三个项目的融资风险进行评价，评价各方案的主要依据是三个决策准则，即债务覆盖率（A1）、债务承受率（A2）、资源覆盖率（A3），这里三个准则都属于效益型指标，对应的权重为［0.36，0.41，0.23］。这些指标会在未来的一段时间、一定区间内波动，对于每个指标，建设项目都有一个底线，公司根据这个底线来对方案的多个指标进行综合的考量，最终选择出风险最小的项目进行开发。而这个底线实际上就是基础设施建设项目融资风险评价的参考点。表1是该决策问题的区间数多准则决策矩阵。每个方案在各准则下的取值都是一个区间数，即方案收益在该准则值下未来可能的波动区间。为简单起见，表1中的准则值都是经过标准化处理后的数据，在［0，1］范围以内。

假定项目融资风险设定的各准则参考点如表2所示。根据准则参考点的取值和各准则前景值的计算方法，将区间数看成是N个离散数据的集合，N取值100，计算方案在各准则下的前景值，如表3所示，其中正值表示获得，负值表示损失。对于式（9）中计算价值函数的参数α、β和λ的取值，这里采用曾建敏的建议，即α＝1.21，β＝1.02；λ＝2.25［19］。而对于式（12）～ （13）中计算权重函数的参数γ＋，γ－和φ，根据Prelec的建议值，取γ＋＝0.8，γ－＝0.8，φ＝1.0［15］。

表1 区间数决策矩阵表

表2 决策准则参考点表

表3 N＝100时方案在准则下的前景值表

方案在各准则下的前景值乘以准则的权重，得到方案总的前景值，如表4所示。可以看出，3个方案的排序结果为D1＞D3＞D2。

从表5～8中可以看出，在N的取值足够大的情况下，根据前景理论所得出的方案总前景值的排序结果均为D1＞D3＞D2。

表4 N＝100时方案的前景值表

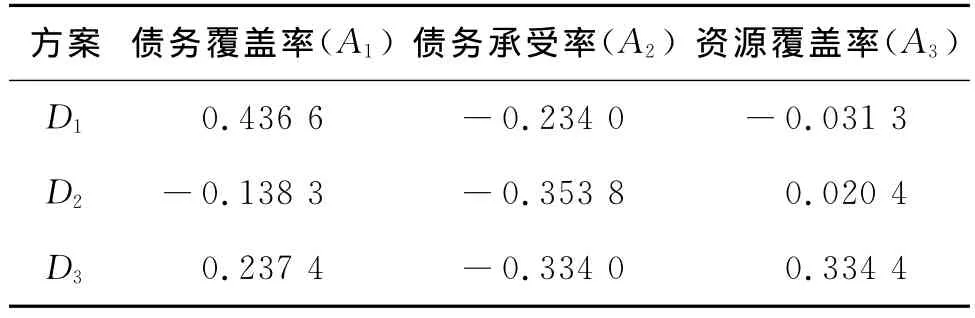
表5 N＝50时方案在准则下的前景值表

表6 N＝50时方案的前景值表

表7 N＝500时方案在准则下的前景值表

表8 N＝500时方案的前景值表

六、结 论

针对准则值是区间数的多准则决策问题，本文提出了一种基于前景理论的多准则决策方法，把原来只在单准则决策问题中应用的前景理论推广应用到多准则决策问题。通过准则值在区间内服从正态分布这一特点，利用正态分布的分布函数来表示区间内准则值的分布规律。由于无法对区间内所有实数进行操作，故采取将区间数用一个含有N项的等差数列来代替的方法。通过对N的不同取值情况下的研究表明，N的取值只要足够大，不同值的N不影响最终决策结果。

［1］ 周光明，刘树人.不确定多属性决策中区间数的一种新排序法［J］.系统工程，2006（4）.

［2］ 张全，樊治平，潘德惠.区间数多属性决策中一种带有可能度的排序方法［J］.控制与决策，1999（6）.

［3］ Von Neumann J，Morgenstern O.The Theory of Games and Economic Behavior［M］.Princeton：Princeton University Press，1944.

［4］ Kahneman D，Tversky A.Prospect Theory：An Analysis of Decision under Risk［J］.Econometric，1979（2）.

［5］ Tversky A，Kahneman D.Advances in Prospect Theory：Cumulative Representation of Uncertainty［J］.Journal of Risk and Uncertainty，1992（4）.

［6］ 孙伟，王久胜，扈文秀.行为决策下的证券市场异象研究［J］.统计与决策，2008（10）.

［7］ 张波涛，李延喜，栾庆伟.认知偏差、财务困境成本与财务保守行为［J］.运筹与管理，2008（2）.

［8］ David K D，Charlie C，Raymond S.Prospect Theory，Aanalyst Forecasts，and Stock Returns［J］.Journal of Multinational Financial Management，2004（4／5）.

［9］ 王正武，罗大庸，黄中祥，王一军.不确定条件下的多目标多路径选择［J］.系统工程学报，2009（3）.

［10］Goda K，Hong H P.Application of Cumulative Prospect Theory：Implied Seismic Design Preference［J］.Structural Safety，2008（6）.

［11］Zank H.Cumulative Prospect Theory for Parametric and Multiattribute Utilities［J］.Mathematics of Operations Research，2001（1）.

［12］Han B，John M.A Characterization of Quality－adjusted Life－years under Cumulative Prospect Theory［J］.Mathematics of Operations Research，2003（1）.

［13］Han B，Ulrich S，Horst Z.Additive Utility in Prospect Theory［J］.Management Science，2009（5）.

［14］胡军华，陈晓红，刘咏梅.基于语言评价和前景理论的多准则决策方法［J］.控制与决策，2009（10）.

［15］Prelec D.Compound Invariant Weighting Functions in Prospect Theory［C］.Choices，Values，and Frames.Cambridge：Cambridge University Press，2000.

［16］Sengupta A，Pal T K.On Comparing Interval Numbers［J］.European Journal of Operational Research，2000（127）.

［17］复旦大学.概率论（第一册）［M］.北京：人民教育出版社，1979.

［18］王中兴，鲁成国，何燕华.区间数多属性决策的一种优化分析方法［J］.黄冈师范学院学报，2005（3）.

［19］曾建敏.实验检验累积前景理论［J］.暨南大学学报：自然科学版，2007（1）.

Multi－criteria Decision Making Method with Interval Number Based on Prospect Theory

HU Jun-hua，XU Qi

（School of Business，Central South University，Changsha 410083，China）

With respect to decision making problems whose criteria values are interval numbers，a multi－criteria decision making method under prospect theory is proposed.This method firstly regardes the criteria value as N arithmetic random numbers in the given interval，and the regularities of criteria value distribution for the interval is expressed by the normal distribution function.Then，on the basis of the given reference points of criteria，the prospect value of criteria for every alternative is calculated by value function and decision weight function，and the prospect value of alternative is acquired by weighted average method.At last，all the alternatives are sorted and the optimal one is chosen according to the prospect values.Feasibility of the method is demonstrated by a simple illustrative example.

multi－criteria decision making；interval number；prospect theory；normal distribution

（责任编辑：崔国平）

C934

A

1007－3116（2011）09－0023－05

2011－04－20

国家创新研究群体科学基金项目《复杂环境下不确定性决策的理论与应用研究》（70921001）；国家自然科学基金项目《报童问题中的决策偏差研究》（71071164）；中南大学中央高校基本科研业务费专项资金资助项目《基于不确定模糊偏好判断矩阵的群决策方法研究》（2010QN25）

胡军华，男，江西高安人，工学博士，副教授，研究方向：决策理论与方法，商务智能；

许 琦，女，甘肃兰州人，管理学硕士，研究方向：决策理论与方法。

【统计应用研究】