＊ 矩阵乘积之迹的不等式

冯秀红,杨主旺

(南京信息工程大学数理学院数学系,江苏南京 210044)

＊矩阵乘积之迹的不等式

冯秀红,杨主旺

(南京信息工程大学数理学院数学系,江苏南京 210044)

研究若干复矩阵乘积之迹的不等式,并利用得到的不等式推出两个 Hermite半正定矩阵乘积的任意次幂之迹的不等式,利用矩阵的分解给出一个 Hermite半正定矩阵任意次幂之迹的不等式,推广了相关结果.

Hermite矩阵;迹;不等式

0 引言与引理

矩阵的迹作为矩阵的一个重要数字特征在计算数学、数值估计、随机控制及其计量经济理论等方面有重要应用.国内外学者对此研究相当活跃[1-11].本文运用矩阵特征值与奇异值不等式的性质,获得m个复矩阵乘积以及 Hermite半正定矩阵任意次幂之迹的不等式,推广了 Yang在文献[7]中的结果.

本文所用记号如下:我们用 I表示单位矩阵,O表示零矩阵,tr(A)表示矩阵A的迹,即矩阵A的主对角线之和或所有特征值之和,λi(A)与σi(A)(i=1,…,n)分别表示n阶矩阵A的特征值与奇异值;|λ1(A)|≥…≥|λn(A)|≥0表示n阶复矩阵A的特征值的递降排序,σ1(A)≥…≥σn(A)≥0表示n阶复矩阵A的奇异值的递降排序.特别地,当A是n阶 Hermite半正定矩阵时,λ1(A)≥…≥λn(A)≥0,且σi(A)=λi(A)(i=1,…,n).如果λi(A)≤λi(B)(i=1,…,n),则记 A≤B,或 B≥A.特别地,当λi(A)≥0时,记 A≥O.A+表示矩阵A的Moore-Penrose逆.

首先介绍本文需要的引理.

引理1[1-2]设A与B是 Hermite半正定矩阵,则

其次,设 B是 Hermite半正定矩阵,则∀ε＞0,B+εI＞O,于是由上面所证λi(A(B+εI))≥0,因为特征值是矩阵元素的连续函数[1],故令ε→0即得所证.

1 主要结果

定理1 设A1,A2,…,Am是m个n阶复矩阵,则

甚至tr(A1A2…Am)有可能是复数.

由引理4可知,当A与B都是n阶 Hermite半正定矩阵时,λi(AB)≥0,(i=1,…,n),则tr(AB)≥0.

定理2 设矩阵A与B都是n阶 Hermite半正定矩阵,k为任意正整数,则

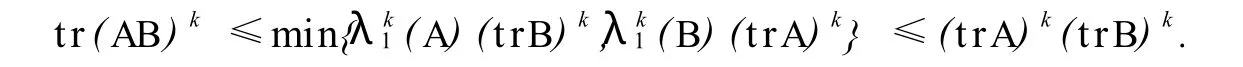
证明 当k=1时,因为 A与B都是n阶 Hermite半正定矩阵,所以σ1(A)=λ1(A),σ1(B)=λ1(B),故由引理4与定理1有

同理,tr(AB)≤λ1(B)tr(A),因而 tr(AB)≤min{λ1(A)tr(B),λ1(B)tr(A)}≤tr(A}tr(B).对于一般情形,由于BAB…AB以及AB…ABA都是 Hermite半正定矩阵,故有

注记4 如果将定理2的条件中B是n阶 Hermite半正定矩阵减弱为B是n阶 Hermite矩阵,此时取k,s为正偶数,m=k+s,则定理3的结论仍然成立.

事实上,因为k,s为正偶数,故可设k=2~k,s=2~s,则m=2~k+2~s,且 B2是n阶 Hermite半正定矩阵,于是由定理2,我们有

[1] Ho rn R A,Johnson C R.Topics in Matrix Analysis[M].Cambridge:Cambridge University Press,1991.

[2] 王松桂,吴密霞,贾忠贞.矩阵不等式[M].2版.北京:科学出版社,2006.

[3] 杨兴东.关于斜 Hermite矩阵乘积之迹的不等式[J].南京师范大学学报:自然科学版,2001,24(1):37-39.

[4] 杨兴东.关于 Hermite矩阵迹的不等式[J].南京气象学院学报,2000,23(1):130-132.

[5] Marshall A W,Olkin I.Inequalities:Theory of Majoration and Its Applications[M].New York:Academic Press,1979.

[6] Wang Bo-ying,Gong Ming-peng.Some Eigenvalue Inequalities for Positive Semi-Definite Matrix Power Products[J].L inear Algebra and Its Applications,1993,184:249-260.

[7] Yang X J.NOTE:A Matrix Trace Inequality[J].Journal of Mathematical Analysis and Applications,2000,250:372-374.

[8] 杨兴东.矩阵之和的特征值与奇异值估计[J].数学杂志,2004,24(3):263-266.

[9] Furuichi Shigeru,Kuriyama Ken,Yanagi Kenjiro.Trace Inequalities for Products of Matrices[J].Linear Algebra and Its Applications,2009,430:2271-2276.

[10] Furuichi Shigeru,Lin Ming-hua.A Matrix Trace Inequality and Its Application[J].Linear Algebra and Its Applications,2010,433:1324-1328.

[11] Komaroff N.Enhancements to the Von Neumann Trace Inequality[J].Linear Algebra and Its Applications,2008,428:738-741.

Trace Inequalities of Product of Matrices

FENG Xiu-hong,YANG Zhu-wang
(College of Mathematics&Physics,N anjing University of Information Science&Technology,Nanjing210044,China)

Some trace inequalities of the product of some comp lex matrices,and derive a trace inequality of the power of product of two positive semidefinite Hermite matrices by using the obtained results.Moreover,we get a trace inequality of the power of a positive semidefinite Hermite matrix by using matrix decomposition,in the mean time,we extend correlative results.

Hermite matrix;trace;inequality

O151.21

A

0253-2395(2011)01-0010-04＊

2010-08-15;

2010-09-30

国家自然科学基金(10871138);南京信息工程大学资助项目(20100076)

冯秀红(1978-),女,山西运城人,副教授,博士研究生,主要从事矩阵的研究和教学.E-mail:fengxh78@163.com