舷侧阵CBF和OBF的阵增益比较

何云峰，宋高顺，焦君圣

(1.南京理工大学机械工程学院精密仪器系，江苏 南京210094；2.杭州应用声学研究所，浙江 杭州310012)

舷侧阵CBF和OBF的阵增益比较

何云峰1，宋高顺1，焦君圣2

(1.南京理工大学机械工程学院精密仪器系，江苏 南京210094；2.杭州应用声学研究所，浙江 杭州310012)

以舷侧阵作为研究对象，首先介绍了常规波束形成器（CBF）和最佳波束形成器（OBF）的波束输出信号模型，然后推导了信号＋噪声场合下的阵增益表达式，比较了在不同信号频率和不同信号源方向角下，CBF和OBF的阵增益，最后在增加了有指向性的CW干扰后，分析了此场合下的阵增益，并比较了不同的信号频率下，干扰源方向角的变化对两类波束形成器阵增益的影响。

常规波束形成；最佳波束形成；阵增益；舷侧阵

舷侧阵是在运动载体比较平直的旁侧安装的均匀线型被动声纳基阵，这样可以获得较大的孔径，降低声纳的工作频率，提高频带宽度。舷侧阵可以增加探测距离，又不影响主载体的机动性。由于固定舷侧阵的载体可能是舰艇、鱼雷等自带动力的高速运动体，使得舷侧阵受到海洋环境噪声影响外，还要受到三类较强噪声源的影响：振动噪声、流噪声和螺旋桨噪声。为了提高舷侧阵的远程微弱信号的检测能力，除了在时域上进行一系列的预处理之外，还必须在空域进行处理。波束成形技术（Beamforming）就是从传感器阵列重构源信号，通过增加期望信源的贡献或抑制干扰源实现信号的分离，提高输出信号的信噪比，抑制有指向性的强干扰。

波束形成器的种类较多，并且他们的宽容性和灵敏度也相差较大，为了选出比较适合舷侧阵的波束形成器，有必要首先对波束形成器阵增益特性进行比较，为此本文对常规波束形成器 （CBF）和基于最大输出SNR的最佳波束形成器（OBF）的阵增益进行了比较。最初的波束形成技术只是通过对传感器阵列在时域上的延时累加或者在频域上的移相相加获得空间增益从而获得目标方位信息，这就是所谓的常规波束形成技术(CBF)[1]；后来人们在常规波束形成技术的基础上提出了各种改进方法，其中一种改进原则就是使期望信号分量功率与噪声分量功率之比为最大，也就是基于最大输出SNR的最佳波束形成器（OBF）。

1 波束输出信号模型

设舷侧阵有M个阵元，阵元间距为d，位于一个各向同性空间均匀的噪声场中，信号源的方向角为φ，频率为f。干扰源在φi方向角产生CW信号序列i（n），干扰、有用信号、噪声互不相关。

1.1 常规波束形成

各阵元接收到的离散信号序列为[2]：

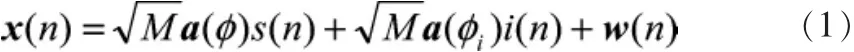
式中：x（n）=[x1（n） x2（n）…xM（n）]T为各阵元接收到的离散信号序列；s（n）为信号源的信号序列；a（φ）为基阵响应向量；w（n）=[w1（n），w2（n）…wM（n）]T为各个阵元上的噪声。

对于波束指向角为θ的波束，其波束输出为:

式中：c（θ）为波束形成器权值向量，对于均匀直线行舷侧阵，有 c（θ）=a（θ）。

1.2 最佳波束形成

当波束指向角为θ时，最佳波束形成器的权向量为[3-5]：

式中：Ri+w为干扰加噪声信号的协方差矩阵。

则波束输出为：

2 信号+噪声场合下的空间阵增益

首先以理想的海洋环境为研究对象，不考虑方向性干扰的影响，因此令上述信号模型中的干扰分量i（n）等于零，即可得到无干扰时的阵元输出信号和波束输出。

2.1 常规波束形成的阵增益

由阵元输出模型，得各阵元接收信号信噪比为[6]：

式中：s(n)，wm(n)分别表示信号和噪声；σ2s，σ2w分别为信号和噪声的功率。

波束形成器的输出信号由信号分量和噪声分量组成，故

式中：Rw为阵元输出噪声信号的协方差矩阵，在各向同性空间均匀的噪声场中，Rw中各元素ρ的大小由信号频率f和阵元间距d决定，具体如下：

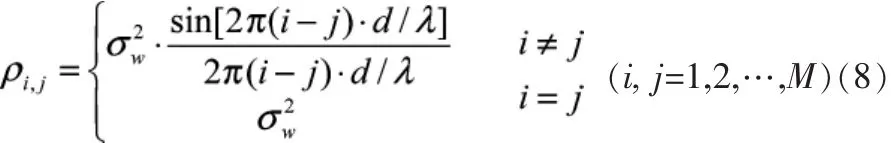
因此波束输出信号的信噪比为:

采用常规波束形成的鱼雷舷侧阵的阵增益为：

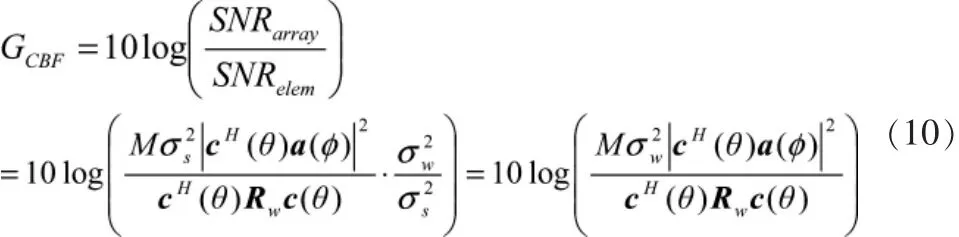
2.2 最佳波束形成的阵增益

最佳波束形成器输出信号中有用信号和噪声成份的功率分别为：

利用式（5）和式（13）可得最佳波束形成的阵增益：

2.3 计算机仿真

式中：Rw为阵元输出噪声信号的协方差矩阵，矩阵中的各元素值可用式（8）计算。

假设均匀线阵有32个阵元，阵元间距d=0.075 m，线阵的水听器没有指向性，设水声的传播速度c＝1 500 m/s。我们将考虑在有用信号的不同频率f下，两种波束形成器的阵增益G随着频率f和信号源方向角（也等于波束指向角θ）变化的规律，如图1和图2所示。在计算Rw-1时，为了减少Rw的特征值分散程度，采用了对角加载方法。从图中看出，随着频率的增加，两类波束形成器的阵增益均增加；在远离正横方向，最佳增益和常规增益都更大，但在f=10 000 Hz时均降至10log(M)dB。

图1 常规波束形成的阵增益

图2 最佳波束形成的阵增益

为了直观比较，分别比较信号频率为5 000 Hz和9 500 Hz时在0～180°方向上的阵增益，如图3和图4所示；以及不同信号频率在方向角为90°和180°方向的阵增益，如图5和图6所示。从图上可以看出，在正横方向附近的空间，随着频率的增加，他们的阵增益也在增大，并且他们的阵增益越来越接近，直到在10 000 Hz时不同的信号源方向角上的阵增益完全相等，均等于10log(M)dB。在远离正横方向的绝大多数频率下，最佳波束形成器的阵增益要比常规波束形成器大，信号源方向越偏离正横方向，阵增益相差越大。

图3 f=5 000 Hz时的阵增益

图4 f=9 500 Hz时的阵增益

图5 信号方向角为90°时的阵增益

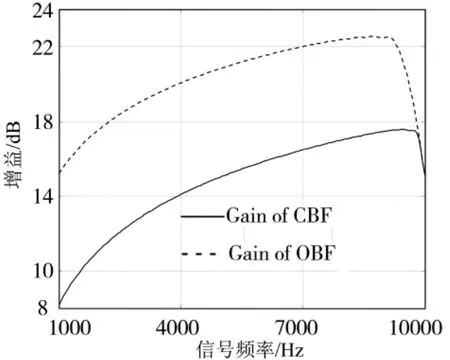
图6 信号方向角为180°时的阵增益

3 信号＋干扰＋噪声场合下空间增益

3.1 常规波束形成的阵增益

若考虑方向性干扰的影响，简单起见，假设干扰信号和有用信号都属于同一窄频带的不相关信号，则

常规波束输出信号的信噪比为：

因此，存在干扰源时的阵增益为：

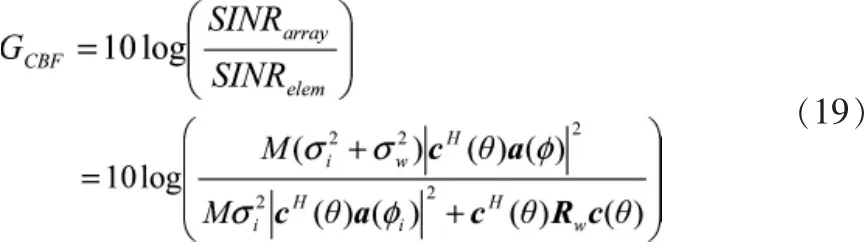
3.2 最佳波束形成的阵增益

参考存在干扰源时常规波束形成的阵增益求法，可得到最佳波束形成的阵增益为：

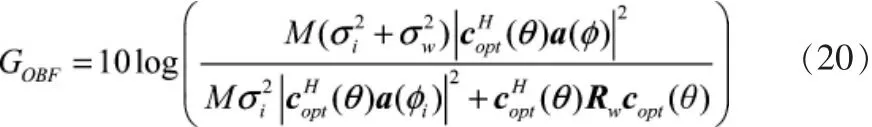
3.3 计算机仿真

令信号源的方向角φ等于波束指向角θ，由于|cH（θ）a（φ）|2=1 和|cHopt（θ）a（φ）|2=1，常规波束形成和最佳波束形成的阵增益分别为：

他们的阵增益与阵元个数、阵元的间距、有用信号的频率、波束指向角和干扰源方向角等有关。如图7和图8所示，图中假设θ=φ=90°，INR＝5 dB，干扰信号和有用信号都属于同一窄频带的不相关信号。从图7和图8仅能看出两种波束形成器在不同的干扰方向角φi和有用信号频率下的阵增益趋势，并比较有用信号频率f=10 000 Hz时，他们阵增益大小，如图9所示。从图上可以看出，OBF的阵增益曲线比CBF的阵增益曲线平坦，且波谷更加陡峭，这表明只有当干扰源非常接近信号源方向角时，OBF的阵增益才会降低；OBF的阵增益对存在于其它方向的干扰源不敏感。

图7 θ=φ=90°时，CBF 的阵增益

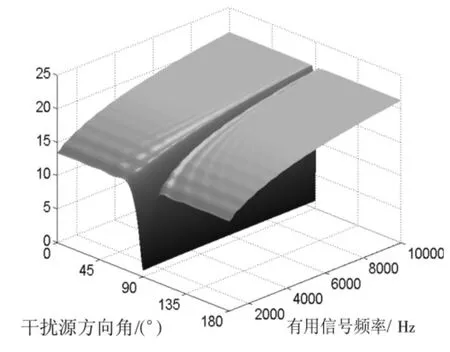
图8 θ=φ=90°时 OBF的阵增益

图9 f=10 000 Hz时 CBF和OBF的阵增益

4 结论

通过以上CBF和OBF的阵增益比较，OBF空间处理增益要比CBF更好，对干扰源的敏感程度也较低。但是在实际工程中，由于有用信号、噪声和干扰是混叠在一起，往往很难将干扰和噪声分别单独分离，因此也就无法利用最佳波束形成。但研究基于最大输出信噪比的最佳波束形成算法，对如何选择适合舷侧阵的其它波束形成算法有一定的理论指导意义。

[1]李启虎.数字式声纳设计原理[M].合肥：安徽教育出版社，2002.

[2]田坦，刘国枝，孙大军.声纳技术[M].哈尔滨：哈尔滨工程大学出版社，2000：63-87.

[3]Rappaport T S,Ed.Smart antennas-adaptive arrays,algorithms and wireless position location[J].Prentice Hall,Englewood Cliffs,1999.

[4]Richard O.Nielsen.Sonar Signal Processing[M].Interstate Electronics Corporation,Anaheim,California.1991：59-65.

[5] 龚耀寰.自适应滤波[M]（第二版）.北京：电子工业出版社，2003：200-203.

[6]Gray D A.Formulation of the maximum signal-to-noise ratio array processor in beam space[J].The Journal of the Acoustical Society of America,1982,72（4）：1195-1201.

Comparison of Flank Array Gain between CBF and OBF

HE Yun-feng1,SONG Gao-shun1,JIAO Jun-sheng2
(1.Department of Precise Instrument,Nanjing University of Sci.&Tech.,Nanjing Jiangsu 210094,China;2.Hangzhou Application Acoustics Institute,Hangzhou Zhejiang 310012,China)

The beam output signal models of conventional beamformer(CBF)and optimum beamformer(OBF)are introduced.The formulation of array gain is deduced in the case of signal plus noise.The array gains of CBF and OBF are compared at different signal frequency bands and different source azimuth angles.Finally,the CW interference is added to the flank array to analyze the array gain.The influences of two kinds of beamfomers on the array gains are compared when the interference azimuth is changing at different signal frequencies.

conventional beamformer;optimum beamformer;array gain;flank array

TB565

A

1003-2029（2011）03-0064-04

2010-09-19

江苏省南京理工大学紫金之星基金资助项目（0907901-50）

何云峰（1974-），男，重庆人，副教授，博士学位，主要研究水下探测与发射技术。