基于分数阶PIλ控制器的单容水箱液位控制

蔡国娟，王德进，刘振全

(天津科技大学电子信息与自动化学院，天津 300222)

基于分数阶PIλ控制器的单容水箱液位控制

蔡国娟，王德进，刘振全

(天津科技大学电子信息与自动化学院，天津 300222)

讨论分数阶 PIλ控制器在单容水箱液位控制中的应用问题，给出了一种基于图解稳定性准则的 PIλ控制器的设计方法.研究了 PIλ控制器的参数稳定域，然后在稳定域内进行系统性能的设计，并提出具体的设计算法.通过Matlab仿真和水箱液位控制系统的实际操作实验，对分数阶PIλ控制器、整数阶PI控制器和常规Ziegler-Nichols参数整定方法进行比较，说明了本文设计方法的有效性和分数阶PIλ控制器的优越性.

分数阶PIλ控制器；水箱液位控制系统；图解稳定性准则

对分数阶控制系统的研究越来越受到人们的重视.一方面，分数阶模型是对一类实际被控对象的更精确的数学模型描述[1]；另一方面，分数阶控制器可以取得比整数阶控制器更好的控制效果[2]，无论是对整数阶被控对象还是对分数阶被控对象.目前，分数阶控制器有 4种类型，即 TID控制器[3]、CRONE控制器[4]、PIλDμ控制器[5]及分数阶相位超前/滞后补偿器[6].文献[7]采用 D-分解法研究了分数阶 PI和 PID控制器的参数稳定域和性能设计问题.文献[8–10]根据各种性能指标约束，通过解析法求解分数阶 PIλ和PDμ控制器的参数，实现参数整定.

本文以单容水箱液位控制系统为工程背景，利用一种可应用于分数阶时滞系统的图解稳定性准则研究分数阶PIλ控制器的参数稳定域和积分阶次λ对参数稳定域的影响，进而在参数稳定域内进行相角裕度性能设计.文中给出 PIλ控制器的一种图解参数整定方法，并与常规的Ziegler-Nichols参数整定方法[11]进行比较.通过计算机仿真和水箱液位控制实验操作，验证了本文方法的有效性和优越性，实现了分数阶PIλ控制器在液位控制系统中的实际应用.

1 单容水箱的建模

众所周知，单容水箱的数学模型可以表示为

式中：k为稳态增益；T为时间常数；L为滞后时间，一般是由液体的长管路传输产生.实验装置中水箱液位的量程为 0～50 cm.首先将出水阀门固定于某一开度，然后采用阶跃响应法[12]，连续做 3次同样的实验，取被测参数的 3组实验数据，求其平均值，得一阶加滞后模型(1)的参数为

2 参数稳定域

考虑单容水箱液位控制系统，如图1所示.

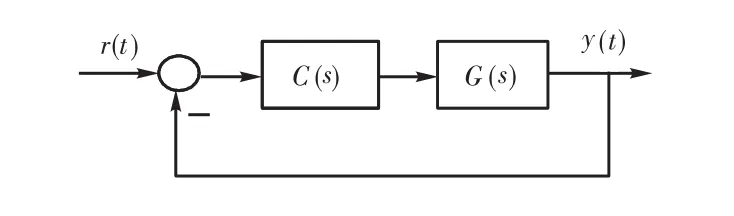
图1 单位反馈控制系统Fig.1 Unity feedback control systems

其中G(s)由式(1)给定，C(s)为分数阶 PIλ,控制器.

式中：kP和kI分别为比例增益和积分增益；λ∈(0,2)为积分阶次.如果取λ=1，就得到常规(整数阶)PI控制器.图1所示系统的闭环拟多项式为

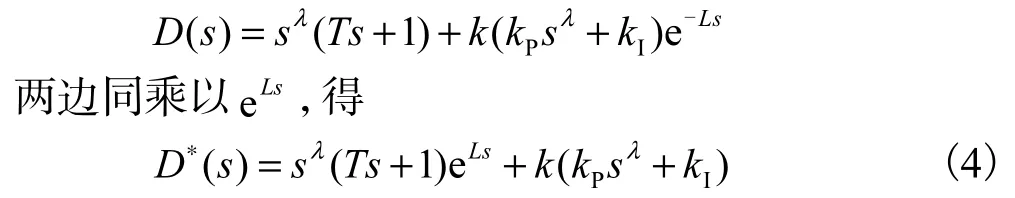
本节的目的是，对固定的积分阶次λ∈ (0,2)，在kP−kI平面，基于一个图解稳定性准则，确定参数稳定域.为此，令s=jω，代入式(4)，得

即虚轴上存在根.由隐函数存在定理可知，如果雅可比(Jacobi)矩阵

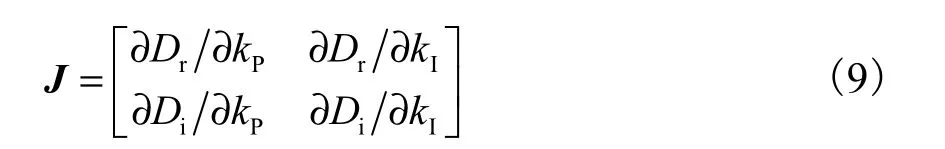
非奇异，则由式(6)和(7)可解得局部唯一连续解曲线(kP(ω) ,kI(ω) ).进一步，有如下命题：

命题1[13]在 kP−kI参数平面上，沿ω增加的方向，当detJ＜0时，参数曲线 (kP(ω),kI(ω) )右侧为稳定的参数区域；而当detJ＞0时，左侧为稳定的参数区域.其中J为式(9)定义的雅可比矩阵.

由式(6)、式(7)和式(9)可以得到

另一方面，以λ和ω为参变量，解方程组(8)得

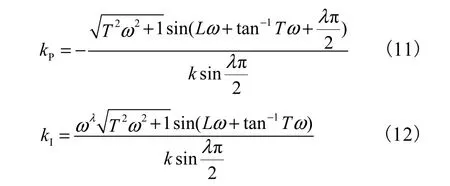
由于特征方程(5)和时滞因子L均为实数，如果jω是式(5)的根，则其复共轭也是式(5)的根，所以只需考虑ω∈ [0,+ ∞ )，对应于两种情况：ω=0和ω∈ (0,+ ∞ ).当ω=0时，令 D∗(0)= 0，得临界稳定边界线

而当ω∈ (0,+ ∞ )时，式(11)和式(12)在 kP−kI平面给出临界稳定边界线的另外一部分，根据命题 1，可以确定该曲线的哪一侧为稳定的参数区域.

3 稳定裕度设计

有了参数稳定域，就可以在稳定域内进行相角裕度(PM)和幅值裕度(GM)的设计.由于相角裕度直接与动态响应的超调量相关，这里只讨论 PM 的设计.设期望的PM为mφ，由PM的定义，开环传递函数应满足式(14).

其中，cω为截止频率.为了获得满意的动态响应，mφ应介于30°～60°.根据式(14)可以定义如下函数：

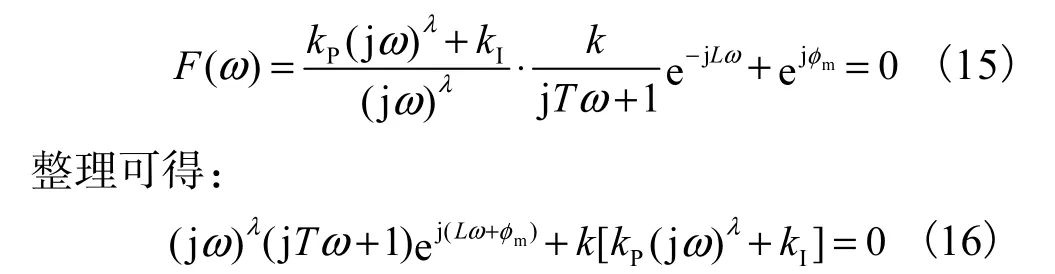
比较式(5)和式(16)，可以看出两式的唯一差别仅在于式(16)多一个因子φm.因此，对给定的PM=φm，上节关于确定参数稳定域的方法完全可以扩展到PM的情形.类似于式(11)和式(12)的推导，有

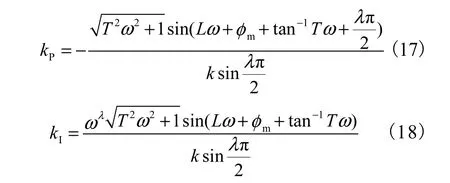
对固定的积分阶次λ，式(17)和式(18)在 kP−kI平面上的稳定域内确定一条满足给定的PM的曲线.

根据上面的讨论，可以提出如下分数阶 PIλ控制器的设计算法.

算法1 给定相角裕度，设计PIλ控制.

(1)选取λ∈ (0,2)，并取足够大的ω，由式(11)和式(12)，在 kP−kI平面上绘制临界稳定参数曲线(kP(ω) ,kI(ω) ).根据式(10)中detJ的符号，由命题 1可判断参数曲线的右侧为稳定域，并结合式(13)得到封闭的参数稳定域.

(2)给定期望的相角裕度φm，由式(17)和(18)，在稳定域内绘制相角裕度曲线.根据命题 1可判断，该曲线的右侧为相角裕度大于φm的参数区域.

(3)沿相角裕度曲线，根据期望闭环系统带宽的要求选择截止频率ωc，并计算出(kP(ωc),kI(ωc)).对于幅值裕度，相对稳定裕度的情形可类似讨论.

4 仿真与实验

对所建立的单容水箱模型(2)，应用算法 1进行分数阶PIλ控制器的设计，并做Matlab仿真与实际液位控制实验.

4.1 确定参数稳定域

对单容水箱模型(2)，应用公式(11)和(12)，在kP−kI平面上，选取不同的分数阶次λ∈ (0,2)，绘制PIλ控制器的参数稳定域，如图2所示.图中箭头为ω增加方向.随λ的减小，参数稳定域变大，为系统性能设计提供了更大的空间.

图2 不同的λ对应的参数稳定域Fig.2 Stability regions for differentλ

本文仅从分数阶 PIλ控制器能有效改善阶跃响应的瞬态性能的角度，讨论了 PIλ的设计问题.λ取0.9，超调量明显减小.λ再小，超调量会更小.但实际上，分数阶 PIλ控制器的另一个特点是能显著改善系统对被控对象增益变化的鲁棒性[9–10].从改善鲁棒性的角度出发，积分阶次λ应相对大一些.这样，动态响应与鲁棒性之间是相互矛盾的，应折衷考虑.所以，仿真与实验中，没有选取过小的λ，而是取λ＝0.9.

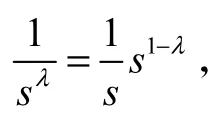
4.2 绘制相角裕度曲线

取λ=0.9和λ=1(整数阶 PI控制器)，给定期望的相角裕度mφ=45°.由式(17)和式(18)，在参数稳定域内绘制相角裕度曲线，如图3所示.

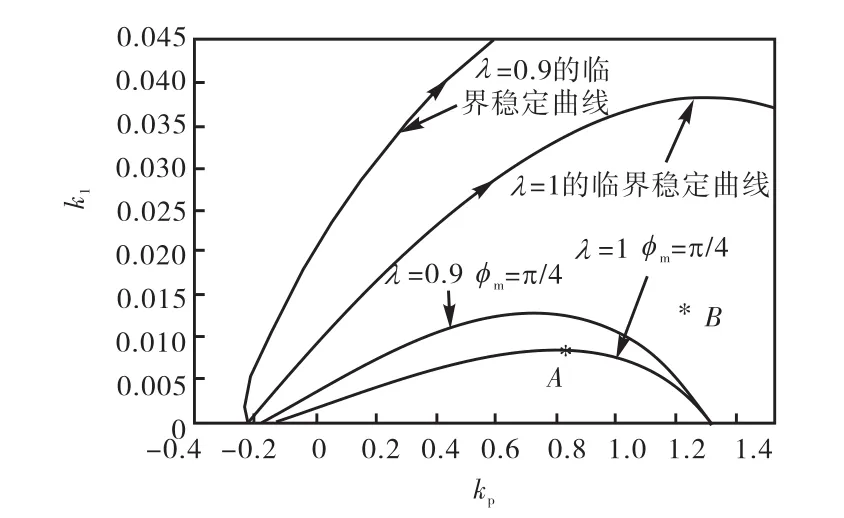
图3 λ=0.9和λ=1的相角裕度曲线Fig.3 Phase margins for λ=0.9 and λ=1

4.3 选择截止频率

根据闭环带宽要求选取截止频率ωc，如图3中A点，其控制器参数为 kP= 0.84,kI= 0.0088.由于A点位于λ=0.9时的相角裕度曲线之内，对于λ=0.9的分数阶 PIλ控制器来说，所达到的相角裕度大于45°，对应的阶跃响应的超调量明显减小，如图 4中点划线所示.

为了比较，图 3中还给出了利用常规 Ziegler-Nichols整数阶PI控制器整定公式算出的参数点B，其控制器参数为 kP= 1.216,kI= 0.0146.相应的阶跃响应曲线如图 4中实线所示.取后，利用 MCGS组态软件编程，在实际液位控制实验装置上进行液位控制实验，测得的3种情况下的阶跃响应曲线如图5所示，与Matlab仿真结果基本一致.

图4 不同参数下的阶跃响应曲线Fig.4 Step responses for different parameters

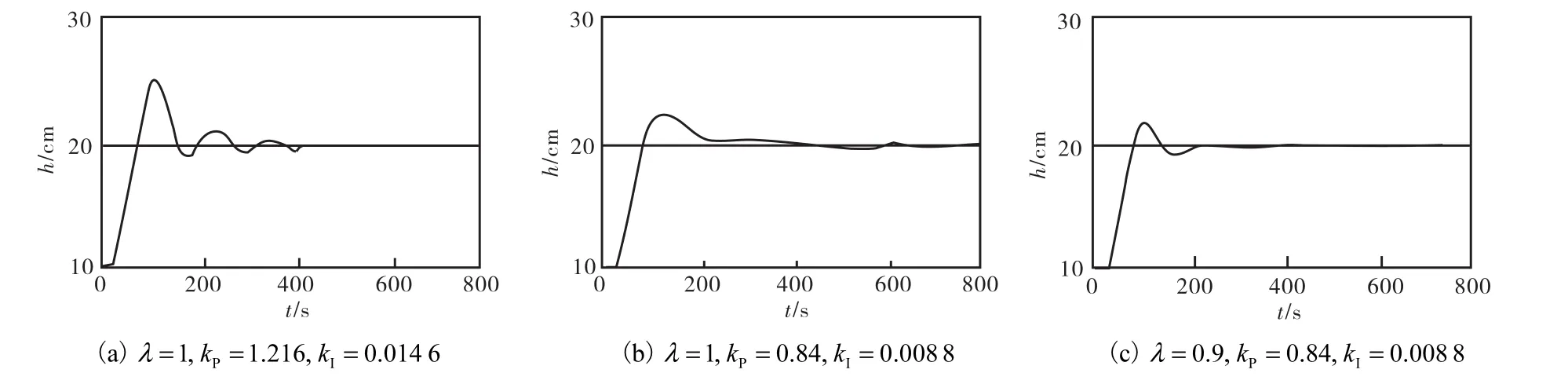
图5 不同参数下的实际液位阶跃响应曲线Fig.5 Actual level step responses for different parameters

5 结 语

本文以单容水箱液位控制系统为工程背景，给出了分数阶 PIλ控制器设计的一种方法.将 Ziegler-Nichols参数整定方法和本文的 PI和PIλ参数整定方法进行了比较，说明了本文方法的有效性，特别是采用 PIλ控制器能有效改善动态响应品质.仿真和实验都说明，分数阶PIλ控制器完全可以取代常规PI控制器，具有广阔的应用前景.

［1］Podlubny I. Fractional Differential Equations[M]. London，UK：Academic Press，1999.

［2］薛定宇，赵春娜. 分数阶系统的分数阶 PID 控制器设计[J]. 控制理论与应用，2007，24(5)：771–776.

［3］Lurie B J. Three-parameter tunable tilt-integral-derivative(TID)controller：US，5371670[P]. 1994–12–06.

［4］Oustaloup A，Mathien B，Lanusse P. The CRONE control of resonant plants：Application to a flexible transmission[J]. European Journal of Control，1995，1：113–121.

［5］Podlubny I. Fractional-order systems and PIλDμcontrollers[J]. IEEE Transactions on Automatic Control，1999，44：208–214.

［6］Monje C A，Calderon A J，Vigagre BM，et al. The Fractional order lead compensator[C]// Proceedings of Second IEEE International Conference on Computational Cybernetics. Vienna，Austria：IEEE，2004：347–352.

［7］Hamamci S E. Stabilization using fractional-order PI and PID controller[J]. Nonlinear Dynamic，2008，51：329–343.

［8］Maione G，Lino P. New tuning rules for fractional PIλcontrollers[J]. Nonlinear Dynamics，2007，49：251–257.

［9］Monje C A，Calderon A J，Vinagre B M，et al. On fractional PIλcontrollers：Some tuning rules for robustness to plant uncertainties[J]. Nonlinear Dynamics，2004，38：369–381.

［10］Luo Y，Chen Y Q. Fractional order [Proportional derivative] controller for a class of fractional order systems[J].Automatica，2009，45(10)：2446–2450.

［11］Ziegler J G，Nichols N B. Optimum setting for automatic controllers[J]. Transaction of the ASME，1942，64：759-768

［12］潘永湘，杨延西，赵跃. 过程控制与自动化仪表[M]. 2版. 北京：机械工业出版社，2007.

［13］Diekmann O，van Gils S A，Verduyn Lunel S M. Delay Equations：Fractional-，Complex- and Nonlinear Analysis[M]. New York：Springer-verlag，1995.

Level Control of Single Water Tank Based on Fractional-Order PIλControllers

CAI Guo-juan，WANG De-jin，LIU Zhen-quan
(College of Electronic Information and Automation，Tianjin University of Science & Technology，Tianjin 300222，China)

The application problem of fractional-order PIλcontroller in the level control of single water tank was discussed，and a design method of PIλcontroller was given based on a graphical stability criterion. The parameters stability region of PI controller was first determined，then，the performances of the closed-loop system were considered in the stability region，and a practical design algorithm was proposed also. Via Matlab simulation and the practical control test in the level control of water tank device，the control effects of fractional-order PIλcontrol，the conventional PI control and the Ziegler-Nichols tuning rule was compared. The results show the effectiveness of the design approach proposed and the superiority of fractionalorder PIλcontrol over the conventional PI control.

fractional-order PIλcontroller；level control systems of water tank；graphical stability criterion

TP273

A

1672-6510(2011)04-0057-04

2011–03–29；

2011–04–25

国家自然科学基金资助项目(60874028)

蔡国娟（1985—），女，吉林白城人，硕士研究生；通信作者：王德进，教授，wdejin56@sina.com.