带位势的耦合薜定谔方程组的基态解
禇心瑞 杨 帆 张亚静
(山西大学 数学科学学院,山西 太原 030006)
带位势的耦合薜定谔方程组的基态解
禇心瑞 杨 帆 张亚静
(山西大学 数学科学学院,山西 太原 030006)
考虑下面的带位势耦合薜定谔方程组,
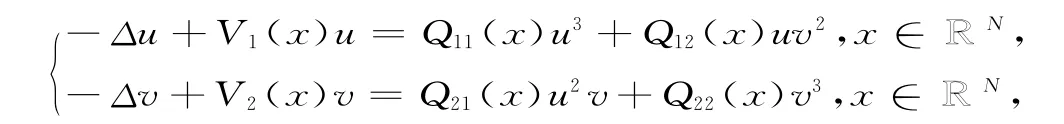
其中 N=1,2,3,Vi(x)和Qij(x)(1≤i,j≤2)是正的连续函数且满足Q12(x)=Q21(x).我们利用Nehari流形和Ekeland变分原理证明了一个半正基本态解的存在及其性质.
基本态;Nehari流形;Ekeland变分原理;能量泛函



[1] Akhmediev N,Ankiewicz A.Partially coherent solitons on a finite background[J].Phys Rev Lett,1999,82:2 661-2 664
[2] Christodoulides D N,Coskun T H,Mitchell M,et al.Theory of incoherent selffocusing in biased photorefractive media[J].Phys Rev Lett,1997,78:646-649
[3] Esry B D,Greene C H,Burke J P,et al.Hartree-fock theory for double condensates[J].Phys Rev Lett,1977,78:3 594-3 597
[4] Genkin G M,Modification of superfluidity in a resonantly strongly driven Bose-Einstein con-densate:American.035604[P].2002-07-03
[5] Hioe F T.Solitary waves for N coupled nonlinear Schrödinger equation[J].Phys Rev Lett,1999,82:1 152-1 155
[6] Ambrosetti A,Colorado E.Standing waves of some coupled nonlinear Schrödinger equations[J].J London Math Soc,2007,75:67-82
[7] Lin T C,Wei J C.Ground state of N coupled nonlinear Schrödinger equations in Rn,n ≤3[J].Comm Math Phys,2005,255:629-653
[8] Lin T C,Wei J C.Spikes in two coupled nonlinear Schrödinger equations[J].Ann Inst H PoincaréAnal Non Linéaire,2005,22:403-439
[9] Barsch T,Wang Z Q.Note on ground states of nonlinear Schrödinger systems[J].J Partial Differential Equations,2006,19:200-207
[10] Lieb E,Loss M.Graduate studies in mathematics[M].Providence:AMS,1997
Ground States of Coupled Nonlinear Schrödinger Systems with Potentials
Chu Xinrui Yang Fan Zhang Yajing
(School of Mathematical Sciences,Shanxi University,Taiyuan 030006,China)
To study the Schrödinger equations with potentials:
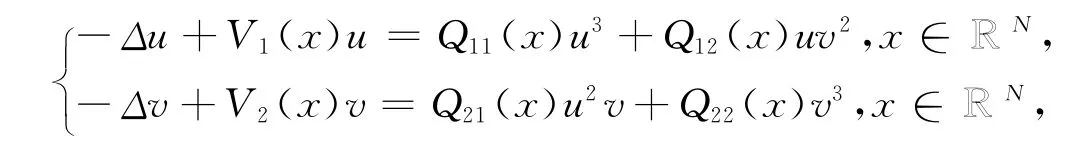
where N=1,2,3,Vi(x)with Qij(x)(1≤i,j≤2)are positive continuous functions satis fying Q12(x)=Q21(x).We use the Nehari manifold and Ekeland′s variational principle to proof the existing of a semi-positive ground state and it′s property.
ground state;Nehari manifold;Ekeland′s variational principle;energy functional
王映苗】
1672-2027(2011)04-0001-03
O177.91
A
2011-07-08
国家自然科学基金(10701051),山西省自然科学基金(2009011008)资助.
褚心瑞(1986-),女,山西侯马人,山西大学数学科学学院在读硕士研究生,主要从事非线性分析研究.

