基于MATLAB的直流调速系统参数研究

杨贺娟,马 骥

(沈阳大学信息工程学院,辽宁沈阳 110044)

基于MATLAB的直流调速系统参数研究

杨贺娟,马 骥

(沈阳大学信息工程学院,辽宁沈阳 110044)

首先介绍了用Simulink搭建转速反馈直流调速系统仿真模型的具体过程.对转速反馈的直流调速系统进行仿真,对系统参数整定,最终得出系统超调量满足5%≤σ≤10%的转速调节器ASR的参数范围.分析调节器参数变化对系统超调量的影响,并得出两者之间的关系.

直流调速;转速反馈;参数整定;仿真;MATLAB/Simulink

1 直流调速系统

直流调速系统以其静差率小、调速范围广、稳定性能好以及具有良好的动态性能等多方面的优点,应用范围十分广泛[1].本文重点介绍了转速反馈直流调速系统调节器的构成、其参数整定过程,并分析了其参数变化规律.

本文中的转速反馈直流调速系统的参数如下:给定输入电压U＊n=10 V,晶闸管放大倍数Ks=40,晶闸管的失控时间Ts=0.001 7 s,电磁时间常数Tl=0.03 s,机电时间常数Tm=0.18 s,电枢回路总电阻R=0.5Ω,电动势常数Ce= 0.132 V·min/r,转速反馈系数α=0.007.系统设计的要求为:系统的超调量满足5%≤σ≤10%.

转速反馈直流调速系统调节器分为比例调节器、微分调节器和积分调节器[2].串联校正系统中,比例调节器的作用是可以提高系统的开环增益,减小系统的稳态误差,提高系统的控制精度.但是会降低系统的相对稳定性,甚至会使闭环系统不稳定.积分调节器有利于系统稳态性能的提高,使相角滞后90°,对于系统的稳定性十分不利.综上,本文采用比例积分调节器完成该系统的参数调节及参数分析.转速反馈直流调速系统如图1所示.

图1 带有比例积分控制器的直流调速系统

图1中,Kp为控制器的放大倍数,τ为积分控制器的积分系数.Kp,τ为系统控制器的可调参数.

2 系统参数整定及临界值的确定

2.1 仿真模型的建立

用Simulink对转速反馈直流调速系统调节器进行参数整定,首先要利用Simulink工具箱搭建系统仿真模型,其具体过程如下:进入MATLAB,单击MATLAB命令窗口工具栏中的Simulink图标,打开Simulink模块浏览器窗口[3].

在模块浏览器窗口中选择所需子模块:按下鼠标左键选中所需模块,拖入模型编辑窗口.连接各个拖入的子模块,组成转速反馈直流调速系统仿真框图[4].

要对系统进行仿真,必须设置各模块的初始参数[5].以系统仿真框图中的Transfer Fcn子模块为例.用鼠标双击该模块,则出现如图2所示的参数设置窗口,按照本设计要求调整该窗口中的参数,最后单击“OK”键.这样就完成了初始参数的设置.按照相同的方法设置其他子模块的初始参数,得到如图3所示的符合设计要求的转速反馈直流调速系统仿真模型.

2.2 参数整定及临界值的确定

经理论计算,当Kp=1.17,τ=0.87时,系统的超调量小于10%.现以这两个数值为依据,对控制器的参数进行整定.对于这两个参数,先固定一个,改变另一个参数值,将不同的参数值分别对系统进行仿真分析,得出系统的最优值与临界值,而后用同样的方法对另一个参数进行设定[6].

单击启动仿真工具条的按钮或选择Simulation→Start菜单项,再双击示波器模块就可以显示仿真结果,这是启动仿真的过程.

图2 参数设置窗口

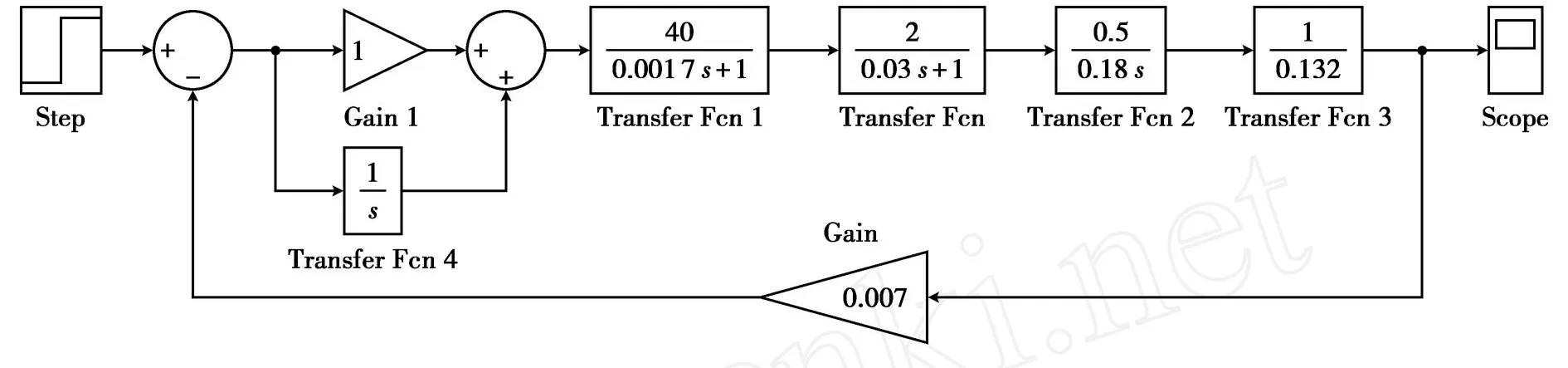
图3 系统参数设定后的仿真模型

如果从显示的仿真结果还不能对阶跃响应的过渡过程有一个清晰的了解,那么就需要对示波器的显示格式作修改.选中Simulink模型窗口的Simulink→Simulink parameters菜单项,打开对话框,对仿真参数进行设置.再一次启动仿真过程,然后启动Scope工具条中的按钮,显示自动刻度(Autoscale),按照图像的大小范围,设置为坐标的上、下限,从而得到清晰的仿真输出曲线.

(1)当Kp=1.17时,τ取不同值,系统的超调量变化如表1～表3所示.

根据系统要求超调量的范围,找出控制器参数的临界值,表2、表3将表1中的τ值细化,以便准确地找出临界值.表2是对确定参数下界的细化表,表3是对确定参数上界的细化表.

表1 τ取不同值时系统的超调量变化表(a)

表2 τ取不同值时系统的超调量变化表(b)

表3 τ取不同值时系统的超调量变化表(c)

根据表1～表3,可知系统当Kp=1.17时,参数τ的取值在0.47～0.77之间满足系统对超调量的要求.

(2)当τ=0.87时,Kp取不同值,系统的超调量变化如表4～表6所示.

根据表4～表6可知,当τ=0.87时,参数Kp在0.65～0.95和1.45～2.05这两个区间内满足系统对超调量的要求.

表4 Kp取不同值时系统的超调量变化表(a)

表5 Kp取不同值时系统的超调量变化表(b)

表6 Kp取不同值时系统的超调量变化表(c)

通过对仿真结果的分析可以得出,Kp= 1.17,τ=0.6和Kp=1.85,τ=0.87,符合设计要求的最优结果.两组参数的仿真结果如图4、图5所示.

图4 Kp=1.17,τ=0.6时的仿真结果

图5 Kp=1.85,τ=0.87时的仿真结果

将图4和图5相比较,图4的超调量σ= 8.4%,图5的超调量σ=8.53%,图5的超调量要大一些,但是图5的上升时间和调节时间要比图4中的小,所以图5的参数设计值使系统更优.

3 结 论

通过对转速直流调速系统的不同参数的仿真可知,在同一输入下,无论控制器参数怎样变化,系统输出稳定值均相同.对于应用比例积分控制器的转速反馈直流调速系统,当Kp取值相同时,随着τ值的降低,超调量σ不断增加;当τ取值相同时,随着Kp的增大,超调量σ先减少后增加,而且参数τ对超调量的影响要比参数Kp大13倍左右.

[1]陈伯时.电力拖动自动控制系统[M].北京:机械工业出版社,2003:35-40.

[2]胡寿松.自动控制原理[M].北京:科学出版社,2001:223 -226.

[3]薛定宇.控制系统仿真与计算机辅助设计[M].北京:机械工业出版社,2005:145-155.

[4]刘洋,范立南.基于MATLAB的直流调速系统仿真研究[J].沈阳大学学报,2010,22(5):11-14.

[5]沈玉吉,万福才,冯丽娜.转速反馈直流调速系统调节器参数整定[J].沈阳大学学报,2010,22(5):15-17.

[6]张晓明,王刚,陈夺,等.转速、直流双闭环直流调速系统仿真及参数整定[J].沈阳大学学报,2010,22(5):18-21.

Parameters Research of Direct Current Governor System Based on MATLAB

YAN G Hejuan,MA Ji
(School of Information Engineering,Shenyang University,Shenyang 110044,China)

The specific process of the simulated model build of speed feedback dc-speed control system with Simulink is introduced.Simulating the speed feedback dc-speed control system,then setting parameters, finally getting the range of the speed regular ASR’s parameters that make the system loop is more than 5%,less than 10%.Analyzing the effect between regular parameters change and the system loop is to get the relation of regular parameters and the system loop.

direct current governor;speed feedback;parameter setting;simulation;MATLAB/Simulink

TM 921.0

A

1008-9225(2011)06-0115-03

2011-06-07

杨贺娟(1988-),女,辽宁沈阳人,沈阳大学硕士研究生;马 骥(1953-),男,辽宁沈阳人,沈阳大学教授.

【责任编辑 刘乃义】