山东地区b值的统计分析

薛靖楠,李 想,张 波,王永旺

(山东大学数学与系统科学学院,济南 250014)

山东地区b值的统计分析

薛靖楠,李 想,张 波,王永旺

(山东大学数学与系统科学学院,济南 250014)

利用山东省内及其邻近海域(34°～39°N,114°～125°E),1996年1月至2009年5月的地震资料,通过最小二乘法及极大似然法对山东地区近年来的b值进行了求解及分析,给出了本区b值的计算结果,讨论了两种方法得到结果的差异,并对近年来b值时序变化的一些特点及其所反映的问题进行了讨论。

b值;最小二乘法;极大似然法;地震活动;统计分析

0 引言

反映地震频度与震级关系的古登堡-里克特公式:lgN=a-bM是地震学中非常重要的经验公式。这个关系表明,大小地震是按一定比例发生的。其中,M是震级,N表示一定时间段中所统计地区内发生的震级大于或等于M的地震个数。a、b是常数,在短时间内同一地区内可以近似认为是恒定的[1]。

b值(即频度-震级关系式中的斜率)具有明确的物理意义,反映大小地震间的比例关系。实验表明,其主要与区域应力水平和地壳结构的均匀程度有关[2]。当区域应力基本不变时,随着地壳结构的均匀程度增强或减弱,b值相应减小或增强;当介质结构基本不变时,随着区域应力水平的增强或减弱,b值相应减小或增大。在一般情况下,b值相对稳定,在1附近波动;其中,大地震前 b值会发生异常变化,通常表现为减小。所以,根据b值的动态变化我们可以预测大地震的发生[3]。其次,根据古登堡公式可以推测出未来一段时间内该地区发生最大地震的震级(即横坐标的截距)[4]。因而,我们可以说b值在整个地震学研究中具有举足轻重的地位。

1 方法与资料介绍

现在地震研究中,用来计算 b值的方法通常有2种:最小二乘法与极大似然法[5]。

1.1 最小二乘法

若我们假设 x和y之间的关系表示成y=a+bx,那么,在 x取 x1,x2,…,xn时,y的取值分别为a+bx1,a+bx2,…,a+bxn,而实际观测到的数据是

y1,y2,…,yn,因此提出目标量L(a,b)=(yi-(a+bxi))2,L(a,b)实际上就是 n对点的偏差平方和。我们要找 a,b,使L(a,b)达到最小。由:

1.2 极大似然法

设总体ζ服从参数为λ的指数分布,密度函数为f(x;λ)=λe-λx,λ >0,x>0。试求参数λ的极大似然估计量。

我们知道,λ的似然函数为

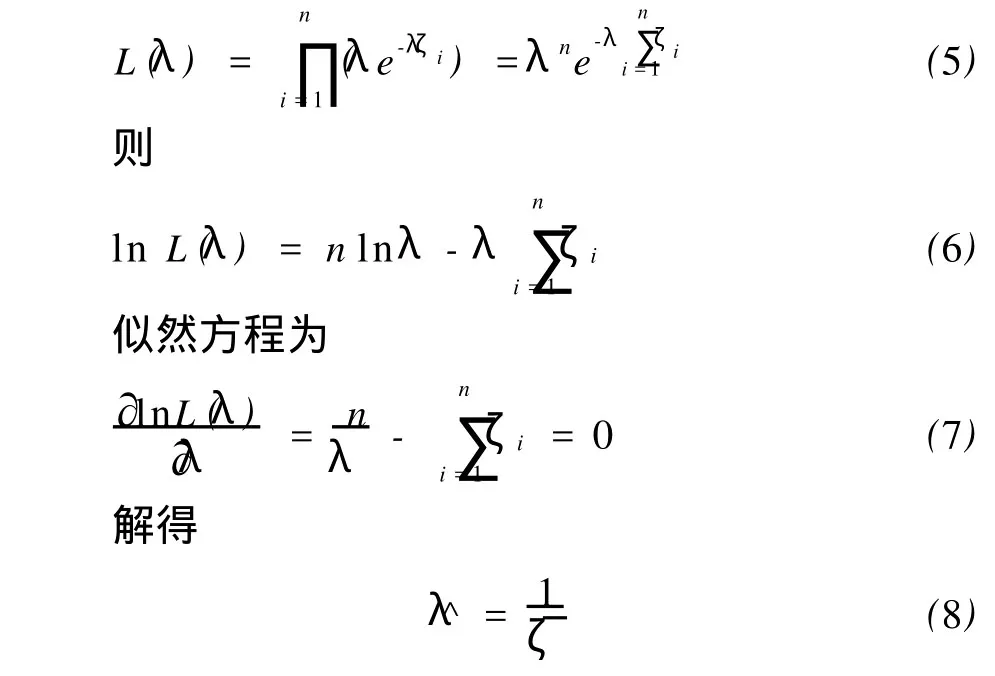
1.3 相关系数检验

在最小二乘法拟合中,最简单的一种检验是相关系数检验,相关系数的定义是

其中 r2越接近于1,说明吻合程度越好

1.4 研究区域简介

山东地区位于华北地震区东南部。本次研究的区域范围为 114°～125°E,34°～39°N。其主要涉及山东内陆及其附近海域。中国东部规模最大的北北东向郯庐断裂带纵贯山东省中部,北北东向聊考及沧东断裂带展布于鲁豫冀交界处,北西向燕山—渤海—威海断裂带穿越渤海直达胶东半岛北部,并与郯庐断裂带交汇在渤海中部。这些大型活动断裂带,也是地球物理异常带及深部地壳变异带。山东内陆及近海还分布着其它许多规模不等、方向不一的次级活动断裂(图1)。这样特定的地质构造背景,决定了山东内陆及近海是一个多震地区。自有历史地震记载以来,山东及附近海域共发生5级以上地震70余次(图2),其中7级以上地震7次,约占华北7级以上地震次数的γ3。其中公元1668年的郯城8.5级地震更是中国东部强度最大的地震,造成山崩地裂、房屋夷平、死亡5万余人,成为旷古奇灾。

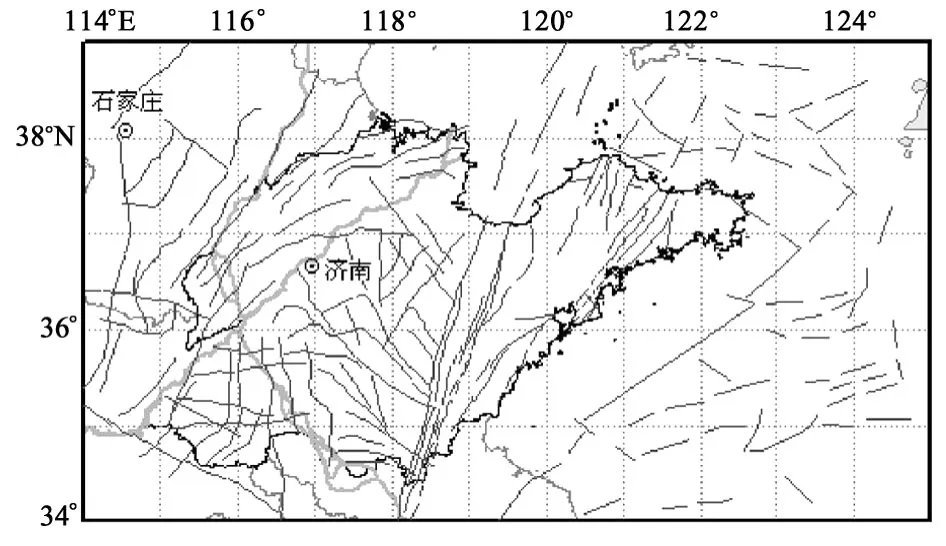
图1 山东地区构造分布图

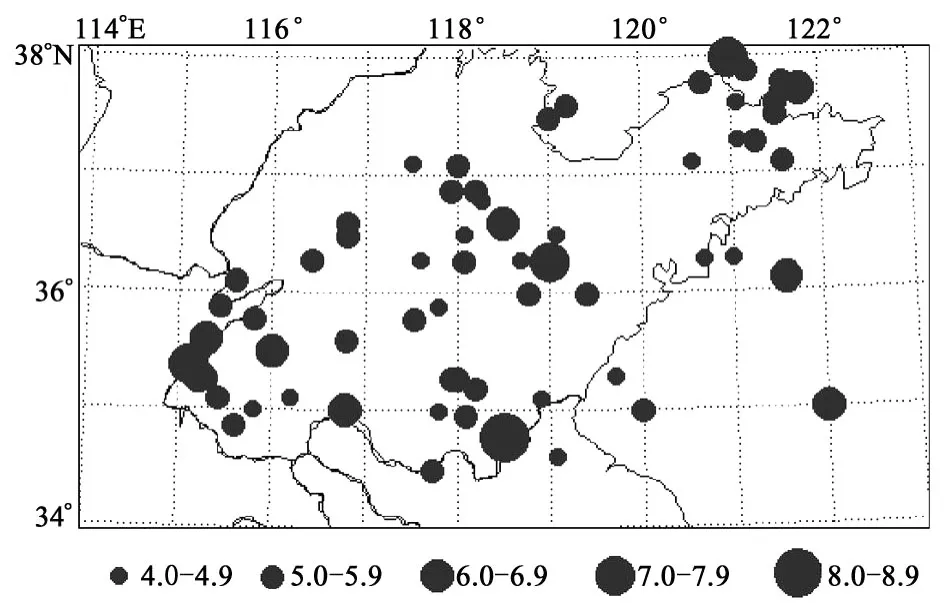
图2 山东地区 MS≥4 3/4地震分布图

2 通过最小二乘法和极大似然法计算b值及最大震级的估计

2.1 利用最小二乘法计算值

使用山东省内及其邻近海域(34°～39°N,114°～125°E)1996年1月至2009年5月期间的地震目录数据,通过最小二乘法进行了地震b值的计算,结果如图3。

货币是指任何一种可以执行交换媒介、价值尺度、延期支付标准和完全流动的财富储藏手段等功能的商品，货币是商品交换发展到一定阶段的产物。货币的本质就是一般等价物。货币可以分为现金、存款、央票、短期银行理财、货币基金等；

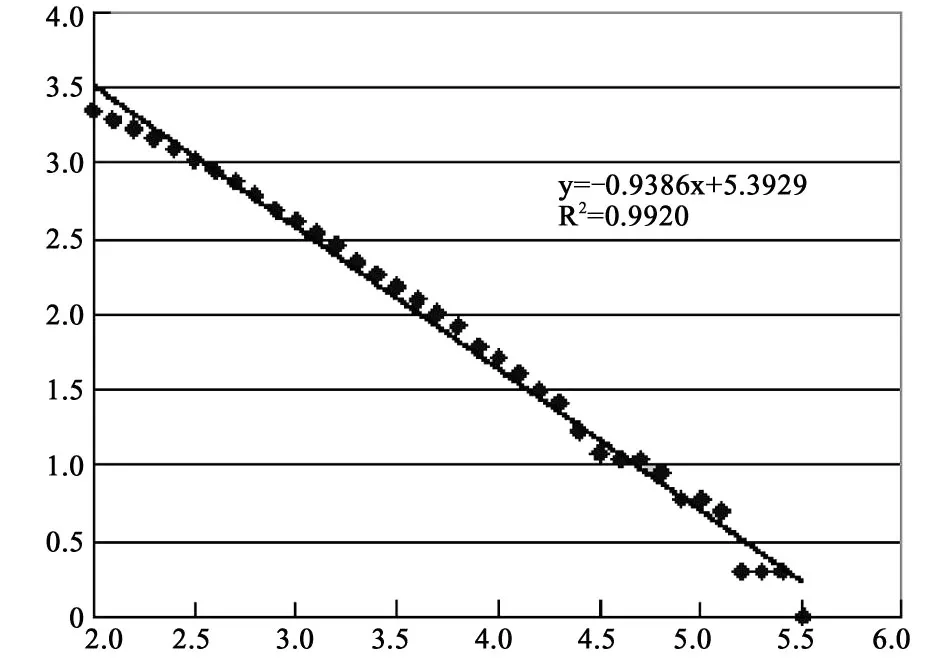
图3 1996年1月至2009年5月山东地区震级频度关系图

首先,我们分别统计了上述范围内大于山东地震台网可以监控的震级 Mi(Mi=2.0,2.1,……,5.5)的地震次数 Ni,然后以震级 M为横坐标,lgN为纵坐标画出散点图。如图3所示。通过图像我们可以非常清晰地看出散点几乎位于一条直线上,这表明了经验公式的准确性。

接着我们通过最小二乘法,综合上述数据,计算出了b值,结果为0.9386,这个b值可以视作山东省近年来b值的平均值或基准值,具体计算方法如下:

由1.1最小二乘法可直接推得古登堡公式lgN=a-bM中a,b的估计值

计算其相关系数的平方,约为0.9920,说明直线吻合得很好。

最后,通过延长直线到横轴,我们得到了其在横坐标上的截距,约为5.74。这即是未来山东地区所发生地震最大震级的估计值

2.2 计算b值的误差分析及克服方法

保证b值准确的条件是:资料准确,样本数足够,计算方法合理。但是通常情况下,这三方面都存在一定的问题,因而导致计算结果误差较大。为了能够在最大限度内减小误差,增强b值的计算准确度,我们采取了抛投法。

由于b值的具体数值与起算震级的选取有关系,因而选取合适的起算震级可以极大地减小误差。这里我们采取抛弃lgN值较小的点(即提高起算震级)来克服“掉头”现象[6](即在 X值较小时,散点常常偏离了直线,接近于曲线。通常认为导致这一现象的主要原因是小震漏记),当然,起算震级也不能选的太高,以免丢失信息。我们根据前人的经验,起算震级从1.5级开始,每隔0.1级做一次 b值计算,并计算出相关系数的平方。结果发现,相关系数从较小值逐渐增大,达到一极大值时又逐渐减小。其中,最大值集中在2.0附近,这与计算得到的台网监测能力基本一致,因而我们选取2.0作为起算震级。

2.3 利用极大似然法计算b值

由lgN = a-bM,我们可以推出 N =eln10(a-bM)(M>M0),从而震级M的概率密度:

通过观察可知,此式即为1.2中密度函数当 x=M-M0,λ=bln 10的特例,因而通过解似然方程可得:

代入数据(依然取起算震级=2.0),求得 b=0.790,这个b值可以视作山东省近年来以极大似然法计算得到的b值的平均值或基准值。

3 近年来b值的长期变化规律及其意义

研究的空间和时间范围仍与第一节相同。

取12个月为单位时间段,1个月为滑动步长,用每12个月的地震记录通过最小二乘法(起算震级仍取2.0)计算出一个 b值,总共得到了150个 b值数据,按时间顺序连成曲线,即图4。注意图中标明的时间是计算b值的终止时间(纵坐标为 b值,横坐标为时间t)。

为了更好地研究b值变化与较大地震的对应关系,我们在曲线图上标明了所有不小于4.5级地震的发生时间(地震参数见表1)。

表1 山东地区1996—2009年4.5级以上地震表

极大似然法的 b值计算结果见图5,由曲线变化形态看,与图4最小二乘法的结果存在一定差异。分析产生这种差异的原因,出现该差异的原因是由于所采用方法对离散数据所设置的偏离权重不同,最小二乘法以离散点到拟合直线的距离为权重,而极大似然法基于概率分布函数,当数据的概率分布函数是正态分布时,极大似然估计与最小二乘估计相同,但在实际应用中,常常会因为我们用于计算b值的数据并不满足正态分布,因而会出现二者计算结果的差异。谢华章通过数值模拟对极大似然法计算b值的条件进行了详细研究,认为震级范围和分档间隔以及参与统计的地震数都对计算结果存在影响,并且认为当参与统计的地震数目较少时,由于个别较大地震随机性的影响,用最小二乘法计算b值可能会产生相当大的系统偏差[7]。

图4 山东地区b值变化曲线图(1996年1月至2009年5月,M≥2.0级地震)

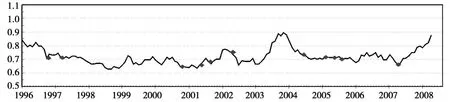
图5 山东地区极大似然法b值变化曲线图

从两种方法的b值曲线图上我们可以看出一些初步结果:

(1)4.5级以上的地震几乎全部集中在曲线的低b值区域,对应关系十分明显。如果按第1节中计算出的最小二乘法b值基准值0.9386,取参考值为0.9,那么可以从图4中看出,所有ML4.5级地震发生时,b值均在参考值之下。同样,在极大似然法的b值变化曲线中,该方法的 b值基准值0.790,取参考值为0.7,则从图5中也同样可以看出,几乎所有的ML4.5级以上地震也都发生在接近该参考值或发生在参考值以下。岩石破裂实验为根据b值动态变化预测地震提供了物理基础。肖尔茨最先从岩石破裂实验中得出,岩石处于高应力状态时,b值低[8],大量的震例研究中发现较大地震前 b值下降[9-10]。

实际上,这种现象并不难理解。我们知道,大地震发生之前一段时间内岩石会发生一些裂隙或微破裂,为大地震即将发生的前兆。起初,岩石破裂程度较小,所以常常只会引发一些较小的地震,小地震的数量增多会导致震级-频度关系图中直线下降更陡,即斜率更大,因而此时 b值较大;而后(即在大地震发生前较短时间内),岩石破裂程度增大,此时中等地震增多,这段时间内直线下降趋势势必变缓,即斜率变小,因而此时b值较小。这就说明了为什么大地震常常发生在低b值之后。

当然,这只是一个普遍情况。实际上,有时候大地震也会发生在高b值之后(例如本次调查中2008年3月的4.8级地震发生时对应的最小二乘法b值就处于相对较高的位置,但此时极大似然法的b值曲线位于极小值)。这种情况一般出现在与地震震级相比研究区范围较大,或地震发生在研究区边缘、外围。2002年4月22日的隆尧5.4级和2008年3月10日的兰考4.8级地震均属于这种情况。

4 结束语

G-R关系是迄今地震活动性研究中普适性最好的统计关系之一,b值物理意义明确,简单易求,现在被不少人用于地震预测研究,尤其在中国应用十分广泛。本文利用现有地震资料,通过最小二乘法及极大似然法对山东地区近年来的b值进行了求解及分析,确定了该区b值的基准值,结果表明山东地区1996年以来12次 ML4.5级以上地震都发生在b值基准值以下。该结果有助于在日常分析预报中确定选择合适的低b值作为异常指标。当然,由于可能存在一些小震的疏漏及方法本身固有的局限性,因而本次b值计算结果多少存在一些误差。同时由于资料的时间尺度短,和我们对震前b值变化机理的认识尚待深入,因此文中的分析和结论也有待进一步验证。最后,衷心希望本文的研究结果能对山东地区的地震预报和地震安全性评价工作有一定的参考价值。

致谢:感谢周翠英研究员和郑建常副研究员的指导和帮助。

[1] 李全林.地震频度-震级关系的时空扫描[M].北京:地震出版社,1979:1-102.

[2] 傅征祥,吕晓健,邵辉成,等.中国大陆及其分区余震序列b值的统计特征分析[J].地震,2008,28(3):1-7.

[3] 黄德瑜,张宇霞.b值时空扫描与地震预报[C]//地震监测与预报方法清理成果汇编(测震学分册).北京:地震出版社,1989:215-223.

[4] 吴开统,张智,焦远碧,等.用b值横截距法预报强余震震级的方法研究[C]//地震预报方法实用化研究文集(地震学专辑).北京:地震出版社,1989:183-193.

[5] 张建中,宋良玉.地震b值的估计方法及其标准误差[J].地震学报,1981,(3):292-301.

[6] 陈培善,白彤霞,李保昆.b值和地震复发周期[J].地球物理学报,2003,46(4):510-519.

[7] 谢华章.b值数字模拟的再研究[J].华北地震科学,1991,9(1):28-34.

[8] 韩渭宾.b值在地震预测中的三类应用及其物理基础与须注意的问题[J].四川地震,2003,(1):1-5.

[9] 边庆凯,李守忠.张北6.2级地震前地震活动性异常及序列特征研究[J].华北地震科学,1999,17(3):35-42.

[10] 陈绍绪,李淑莲.2000年6月25日唐山4.4级地震预测实践[J].华北地震科学,2000,18(4):53-57.

Statistical Analysis of B-values in Shandong Area

XUE Jing-nan,LI Xiang,ZHANGBo,WANG Yong-wang
(School of Mathematics&System Science Shandong University Jinan,Shandong 250014)

Based on small earthquakes data,this paper calculates and analyzes b-values from 1996Jan.to 2009May.in Shandong area using the least square method and maximum likelihood method and compares these two methods based on the results.Finally,we discuss the characteristics of b-values temporal variation in Shandong area and problems reflected by it.

b-value;least square method;maximum likelihood method;seismic activity;statistical analysis

P315.5

A

1003-1375(2011)01-0001-05

2010-09-01

薛靖楠(1990-),男(汉族),山东济南人,山东大学数学与系统科学学院在读学生,主要从事概率统计研究.E-mail:xjn1990@126.com.