递归神经网络原理及其动态补偿器的设计

冯 潇

(苏州大学)

递归神经网络原理及其动态补偿器的设计

冯 潇

(苏州大学)

从介绍动态补偿设计的意义出发，重点分析了递归神经网络原理及其动态补偿器的设计原理，最后用仿真实验证实了设计的可靠性.

智能控制;递归神经网络;传感器;误差;动态补偿

1 问题提出

1.1 智能控制系统现状分析

(1)分级控制系统

该系统又可以称之为:“分级递阶智能控制”，其运行最重要的是依赖于自组织控制和自适应控制等等前提条件.该控制系统在控制过程中涉及到:组织级、协调级和执行级3个方面，同时控制时，对于每个级都有着自己独立的作用.

(2)学习控制系统

这是对人脑的模拟，从人类大脑学习的角度考虑，学习表现出来的是智慧能力的高低.学习控制系统通常情况下，是首先对内部结构完成辨别、认知、调整等一系列活动后，凭借对信号的循环输入和对数据的综合分析与处理，进而确保有着一个良好的运行效果.大量理论研究和实践表明，该控制系统还可以结合很多非预知的信息完成自动控制.

(3)专家控制系统

如图1所示，该智能系统在运行中是把人的经验、知识和技能进行融合并以一种特定的形式表现在计算机系统之中.其控制上是以对应的程序指令为运行操作的依据的.在该系统中，通常情况下将很多理论知识囊括在其中，丰足的理论知识让智能系统处理实际问题时有更多的支撑面，直接体现为处理的结果具有诸多的高性能.

图1 专家系统结构框图

(4)神经网络系统

该系统也是目前运用最多的人工神经网络控制系统.该结构形式综合了神经细胞、人工神经元等等综合处理构成的该模式，具有非常高的前沿性，神经网络系统的主要功能是智能控制与模仿真人，是现代技术研究领域中的新课题内容.

1.2 动态补偿器设计的意义

质量参数信息的实时、在线、动态测试对于现代企业的生产来说尤为重要，是企业对生产实施质量控制的重要依据.理论研究和实践表明，对于随时间迅速发生变化的质量参数，要想利用传感器对其实施测量时，一般的传感器存在着一定的响应滞后，如此一来必然造成了与真值相比测量结果的动态误差比较大，造成检测精度的不足和质量控制准确性的缺失.实践研究表明，可以从以下两个方面着手来提高传感器的动态响应特性:

(1)改变传感器的结构、设计及其参数;

(2)对传感器的输出实施后续处理，设计动态补偿器.

伴随着计算机技术的进步和发展，目前就提高传感器的动态响应特性这一问题，第二种方法到了较为广泛的应用.

目前动态补偿器的设计常见的方法有零极点配置法、系统辨识法等.不过，笔者在研究中发现这些设计方法都必须在事前就选定好动态补偿器的结构，如果涉及的传感器特性属于高阶系统的情况，对应的动态补偿器结构设计相当的复杂.鉴于这个原因，笔者借助此文跟大家分享一种运用递归网络模型对传感器进行动态补偿设计.

2 递归神经网络的结构

递归神经网络(Reeurrent Neural Networks)是具有反馈的网络，是一种极具有选择潜力的动态网.如图2所示为内时延递归型反馈网络结构，从图形上可以看出该网络由输入层、输出层和隐层构成，不过只有隐层节点具有时延反馈.

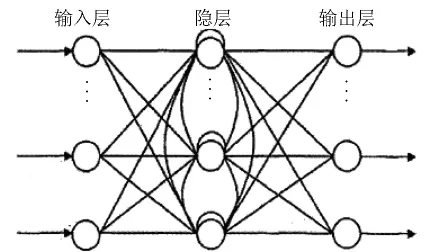
图2 内时延递归型反馈网络

如果将网络外部输入时间序列设为X(t)，将隐层输出设为O(t)，将网络输出设为Y(t)，那么可以对网络进行描述，得到:

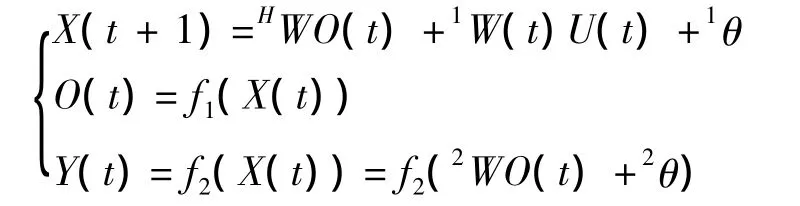
注:上式中，1W、2W和HW分别是输入层至隐层、隐层至输入层以及隐层节点之间(包括节点自身)的连接权值矩阵;其中的f1(·)和f2(·)是非线性作用函数.

3 动态补偿原理及其设计

3.1 动态补偿原理分析

可以借助非线性自回归滑动平均模型(NARMA)来表示一类广泛的离散时间非线性系统，NARMA模型结合自变量是输入、输出噪声的延迟信号的非线性函数实现非线性过程的表述.假设传感器的模型可以用如下的NARMA模型加以表示:

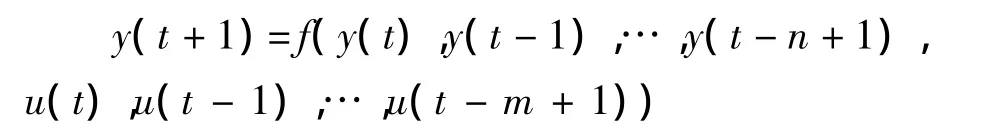
式子中，传感器的输入用u(t)表示，输出用y(t)表示;n和m是未知的，分别用来代表输出和输入的最大延时;f(·)是一种非常复杂的非线性函数关系，通常较难用某种统一的模型来表示.

如图3所示，假设传感器的输入u(t)，输出y(t)，那么这两者之间必然存在着一定的动态测试误差.

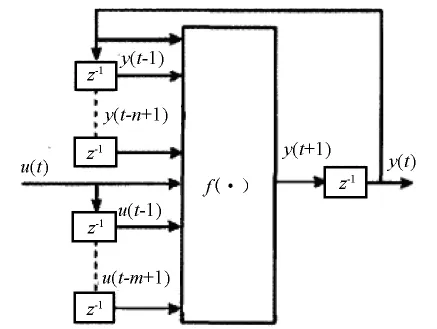
图3 传感器模型

从理论上分析，要想对动态测试误差实施补偿，可以将y(t)通过如下补偿环节:

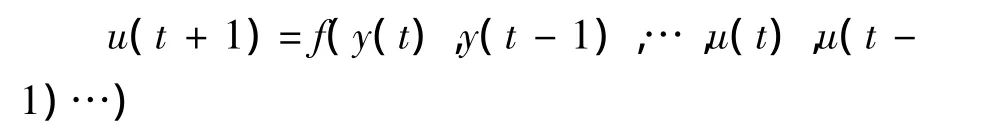
上式中f(·)是某种非线性函数关系，只需要把式子所表示的系统与测试系统进行串联，就能够对传感器实施动态补偿，当然由几个关系式可以得到，通过这种方式补偿后的传感器输入、输出特性与f(·)关系十分密切，会随着f(·)而发生变化.

3.2 动态补偿设计

如图4所示为基于递归神经网络模型的传感器动态补偿示意图.图4中y(t)表示为所期望的传感器特性的输出.可以借助某种训练算法把起关键性作用的递归神经网络的权值加以确定.

3.3 动态补偿的一般步骤

结合上面的理论分析，可以把应用递归神经网络对传感器进行动态补偿的步骤进行如下的归纳:

(1)结合传感器的特性，选定期望的传感器特性;选定递归神经网络的中间层节点数.

(2)获取有关的实验数据，运用RPE算法训练递归神经网络模型，最终得到权值收敛为止.

(3)将递归神经网络模型与传感器进行对接，对传感器进行动态补偿.

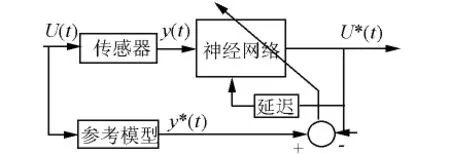
图4 基于递归神经网络的传感器动态补偿

4 仿真试验

笔者对热电偶的测量滞后运用上文中的原理进行了误差补偿的仿真试验.先将试验过程做如下介绍:

(1)选取参考模型具有较大的固有频率的二阶低通滤波器

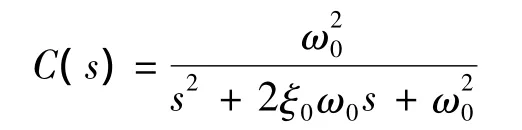
上式中，ξ0为阻尼(ξ0=0.8)，ω0为固有频率(ω0=2πrad/s，远大于热电偶的固有频率)，当然在选取时也不能那个选取得太大，过大的话会导致相当严重的高频噪声污染，甚至有淹没有用信号的可能，如此一来根本没有办法实施测量.

(2)逆模型补偿器的脉冲响应传递函数H(z－1)为:

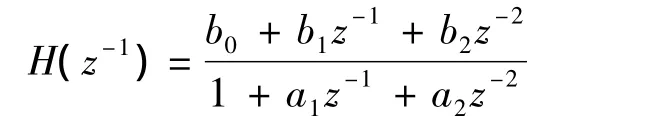
补偿器 G(z－1)的参数为(a1，a2，b0，b1，b2)，阶跃激励下的传感器输出作为补偿器的输出，参考模型输出作为希望输出.

(3)补偿结果分析，补偿结果如图5所示.

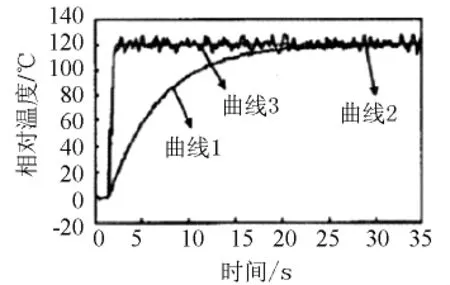
图5 热电偶阶跃响应曲线

在图5中，曲线1表示的是阶跃信号ΔT=120℃时，传感器的输出响应;曲线2表示的是通过动态补偿后，但是未曾消除噪声滤波处理的输出结果;曲线3表示的是经过通过动态补偿后，又经过消除噪声滤波处理后输出结果.

通过仿真实验，可以看出通过该种补偿处理后，动态性能指标有了明显的改善.

［1］于双和，强文义.无抖振离散准滑膜［J］.控制与决策，2001，16(5):32－36.

［2］刘刚，刘学仁.基于递归神经网络的加速传感器动态特性补偿［J］.传感器与微系统，2007，26(7):42－47.

［3］高为炳.变结构控制的理论及设计方法［M］.北京科学出版社，1998.

The Principle of Recurrent Neural Network and the Design of Dynamic Compensator

Feng Xiao
(Suzhou University)

In this paper，the principle of recurrent neural network and the design of dynamic compensator accompanied with presenting the significance of the dynamic compensation are analyzed.Furthermore，the simulation results show the reliability of design.

Intelligent control;Neural network;Sensor;Error;Dynamic compensation

2011－01－24

(责任编辑:李佳云)