地下结构对工程场地地震动场的影响1

朱小乔 楼梦麟 孔祥海

（同济大学土木工程防灾国家重点实验室，上海 200092）

地下结构对工程场地地震动场的影响1

朱小乔 楼梦麟 孔祥海

（同济大学土木工程防灾国家重点实验室，上海 200092）

本文以日本神户市地铁大开站为工程背景，应用大型通用有限元ANSYS软件，分别建立了自然条件下的工程场地土层和建有地下车站结构的土层的二维有限元分析模型。计算了基岩一致地震动输入模式下2个土层模型的动力反应。通过将2个土层模型的动力反应进行比较分析，讨论了地下结构对工程场地地震动场的影响。分析结果表明，日本神户地铁大开站的存在对其邻近区域土层的地震反应有影响，但影响有限。

地下结构 一致地震动输入 工程场地 地震动场

引言

近几十年来，地下结构在城市建设、交通运输、国防工程、水利工程等各个领域得到了越来越广泛的应用（钱七虎，1999；2000）。特别是在地铁已成为当今城市的主要交通工具后，地下结构工程的安全性更是引起了人们的广泛关注。在城市地铁中，地铁一般穿越的地区多为地面建筑密集区，特别是有多条地铁交汇车站的周边地区，更会建有大量的高层建筑。如1995年日本阪神地震中，神户市大开地铁站有一半以上的中柱完全坍塌，导致顶板坍塌破坏和上覆土层的沉降，最大沉降量达 2.5m（庄海洋等，2008）。为此，地下结构的地震反应问题引起了国内外学者的广泛重视，同时也进一步加强了对地下结构抗震减灾的研究。其中最主要的研究包括：地下结构地震反应的理论分析（匡志平等，2002）、数值模拟（Jun等，2002）和模型试验（杨林德等，2003）。

目前在重要工程的工程场地安全性评价中，一般按天然场地进行土层地震反应分析而不考虑地下结构的影响，当地震发生时，由于大型地铁车站的存在，会改变地震波在土层中的传播方式，这势必会影响地下结构周围的土层地震动场的分布状态。然而，目前对此问题的研究还不及对地下结构地震反应问题研究的深入。

本文以日本神户市大开地铁站为例，基于有限元软件 ANSYS，建立了自然条件下的工程场地土层和存在地下结构后的土层二维有限元计算模型，计算了2个模型在水平地震波一致输入下的线性地震反应。通过数值计算结果的对比分析，讨论了由于地下结构的存在对工程场地地震动场，特别是对场地地表、地下结构中心线和侧边轴线上的土层节点运动状态的影响。

1 计算模型

1.1 计算模型的参数

首先将神户大开地铁站所在工程场地土层的地震反应问题简化为二维平面应变问题，采用ANSYS程序计算。当采用有限元法进行土层地震反应分析时，将水平两侧边界无限远的土层有限化，即在土层两侧设置竖向人工边界。考虑到土介质的阻尼性质，当把竖向人工边界设置在离开土层计算近场区较远处时，人工边界对计算近场的地震反应的影响可以忽略，一般要求竖向人工边界设置在距离近场区5倍土层深度的远处（楼梦麟等，2003），具体模型的尺寸见图1（图中黑粗虚线部分为地下结构，其余部分为周围土层），地铁站截面见图2。土层采用Plane42单元进行模拟，地下结构部分采用Beam3单元进行模拟。在进行网格划分时，考虑以下原则：一方面是波动对网格划分的要求，如果单元尺寸过大，则波动的高频部分难以通过；另一方面是求解精度对有限元网格划分的要求，单元网格越细，自由度越多，计算精度越高，但计算所需时间和计算量也会增大。综合考虑后，单元各方向尺寸要小于地震波中高频部分波长的1/8，本文采用的有效高频为12Hz，具体有限元网格划分结果见图3（自然条件下的场地土层模型，共3069个自由度）和图4（建有地下结构的场地土层模型，共4058个自由度）。

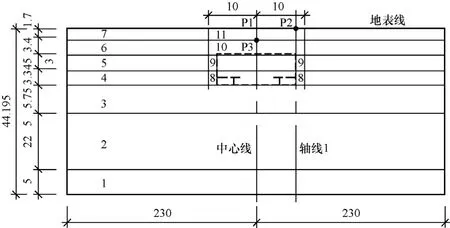
图1 几何模型（单位：m）Fig. 1 Geometric model(unit: m)

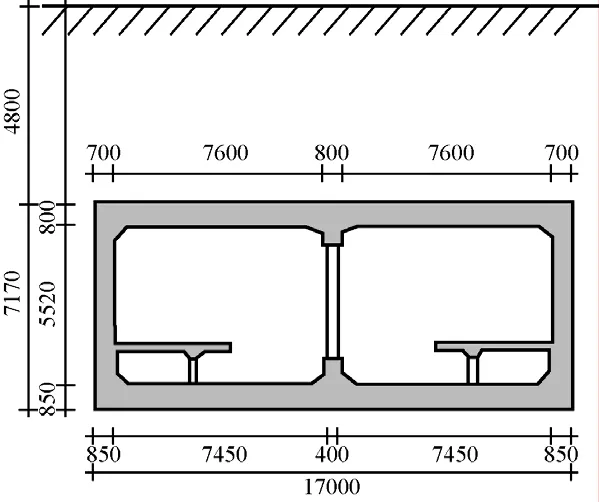
图2 地铁站截面图（单位：mm）Fig. 2 Cross-section diagram of subway station (unit: m)

图3 自然条件下的场地土层模型Fig. 3 Finite element model of the soil site in natural condition

图4 建有地下结构的场地土层模型Fig. 4 Finite element model of the soil site with underground structure

工程场地土层的主要分布为：表层为填土，下面为淤泥质粘土，N值小于10，其次为砂砾层及海相粘土，砂砾层的N值在30—35之间，海相粘土的N值为10左右，15m以下为N值大于50的更新世砾层。土层的物理参数见表1，表中土层编号如图1中所示。

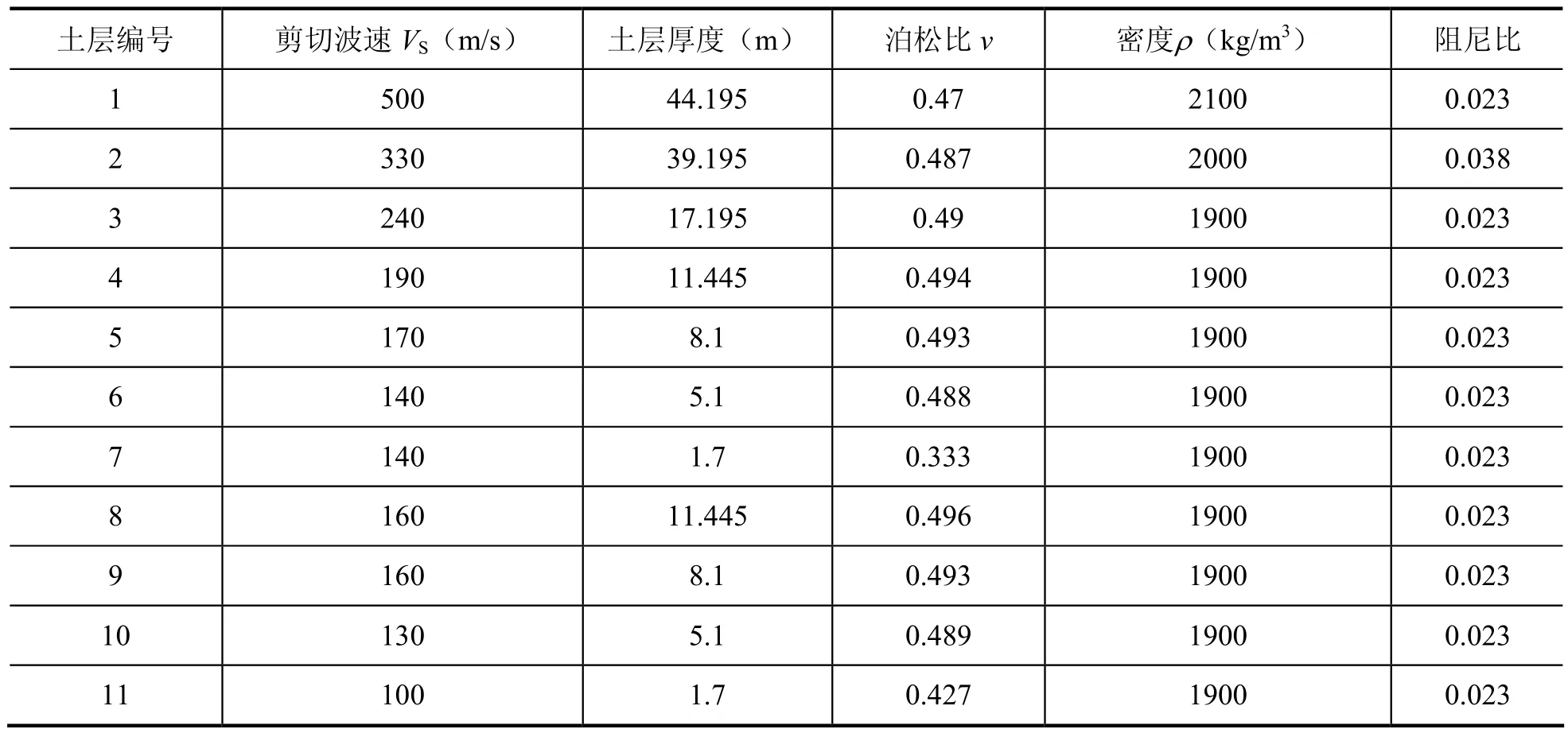
表1 神户地铁车站场地土层的物理参数Table 1 Physical parameters of soil at subway station in Kobe city

1.2 运动方程

经过有限元离散后，半无限土层体系转化为近似的有限自由度的计算体系，沿土层下卧基岩面输入水平地震波，有限自由度体系的地震反应分析方程为：

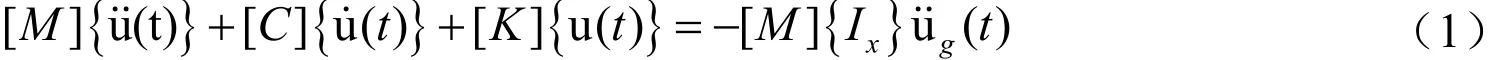
1.3 输入地震波

本文计算所采用的输入地震波为阪神地震中由神户市附近的观测站采集到的东西向地震波，基础加速度峰值调整为98.1cm/s2，地震波如图5所示。

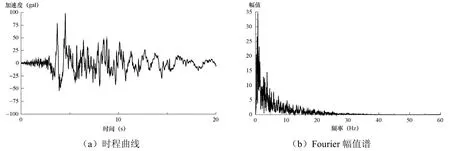
图5 地震波Fig. 5 Input seismic wave

2 场地地表运动状态的比较分析

为了考虑建有地下结构后对场地地震动场的影响，定义如下地下结构影响系数：

式中，Rd和R0分别为建有地下结构和自然状态下土层同一节点处的地震反应量的峰值。

土层在一致地震动输入下是对称结构在反对称作用下的动力反应问题，为了简化分析过程，取2个土层模型右半边的土层运动状态进行对比分析。为了使分析结果具有代表性而又不失一般性，选取图1所示的地表线、对称中心线和侧边轴线1上的土层节点的运动状态作为研究对象。

2.1 地下结构对地表运动状态的影响

在一致地震动作用下，地下结构对地表上的土层节点的水平位移峰值、速度峰值和加速度峰值的影响系数如图6所示，图中坐标原点为图1中的P1。

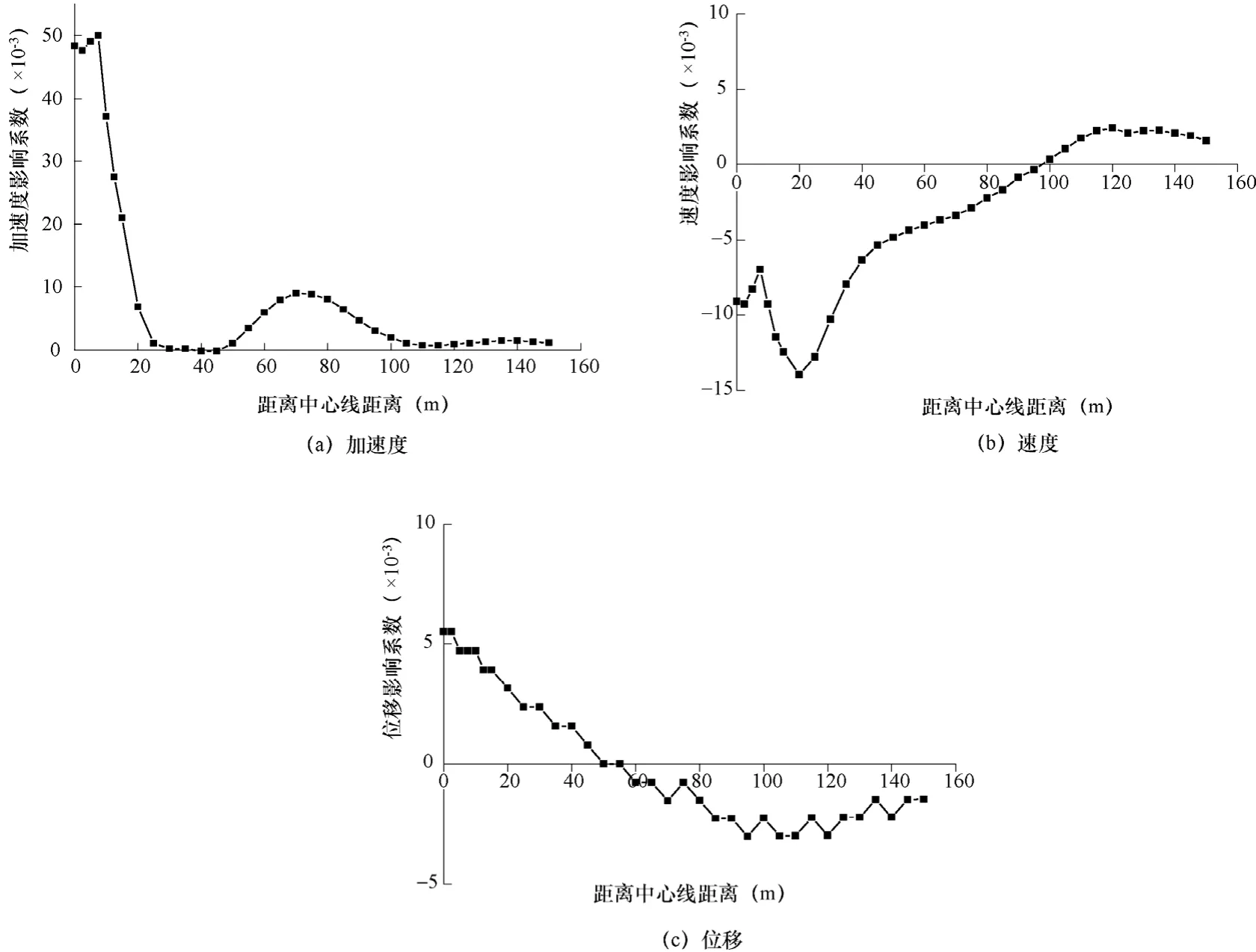
图6 地下结构对地表线运动状态的影响系数Fig. 6 Influence coefficient of underground structure to ground surface motion

从图6可以看出，地下结构的存在对地表的速度峰值和位移峰值影响很小，影响系数分别不足2%和1%；而对地表加速度峰值影响最大的是地下结构角点正上方的地表处及其邻近区域。与自然状态下相比，该区域加速度峰值的最大增幅为5.2%。随着离开地下结构外缘距离的增加，地下结构存在增大了地表加速度峰值的影响将逐渐减小。图7给出了节点P2处的运动状态时程，从图7可以看出：反应时程的波形几乎不变，主要是反应量大小有所差异。

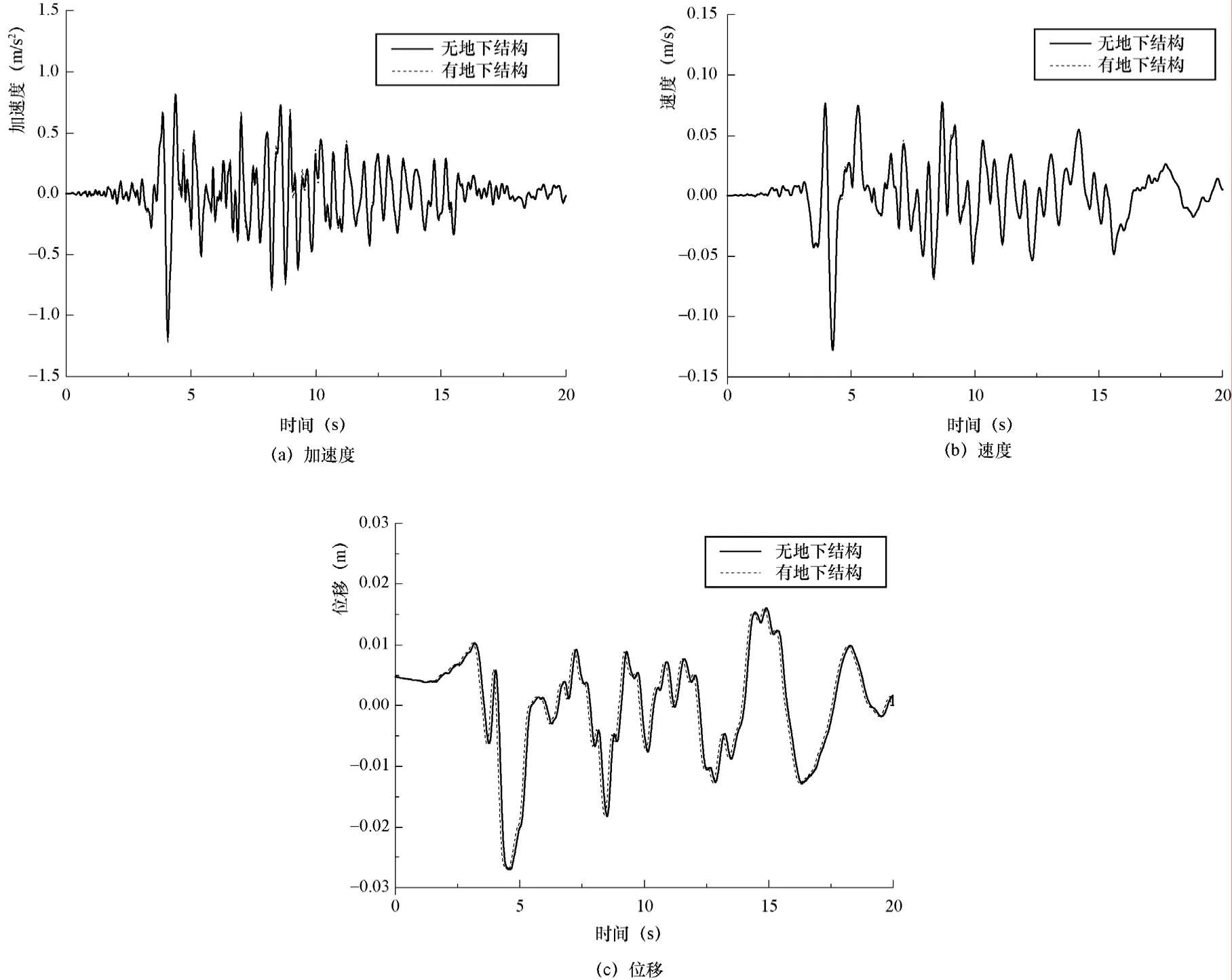
图7 节点P2处运动状态时程Fig. 7 Motion time history of node P2

2.2 地下结构对中心线上土层节点运动状态的影响

在一致地震动作用下，地下结构对中心线上土层节点的位移峰值、速度峰值和加速度峰值的影响系数如图8所示。

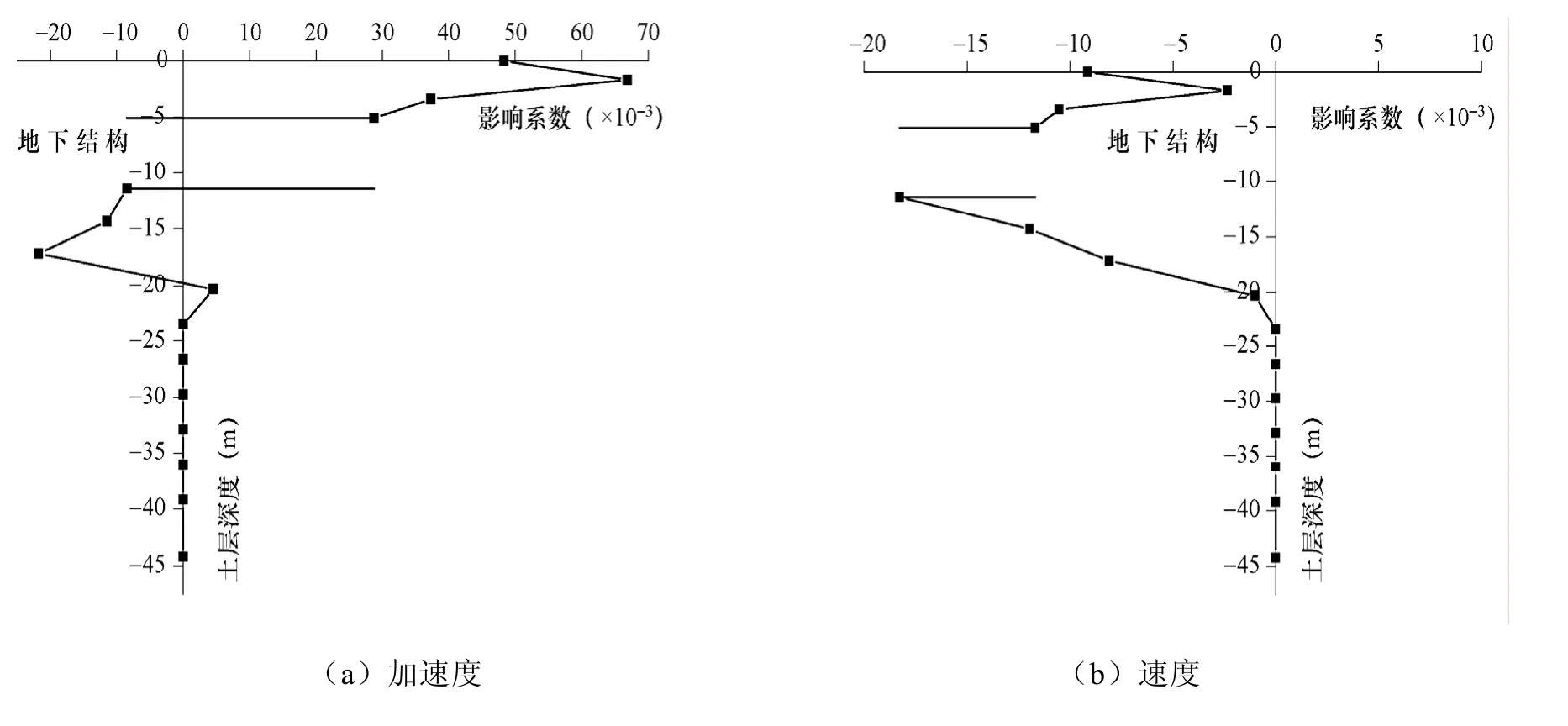
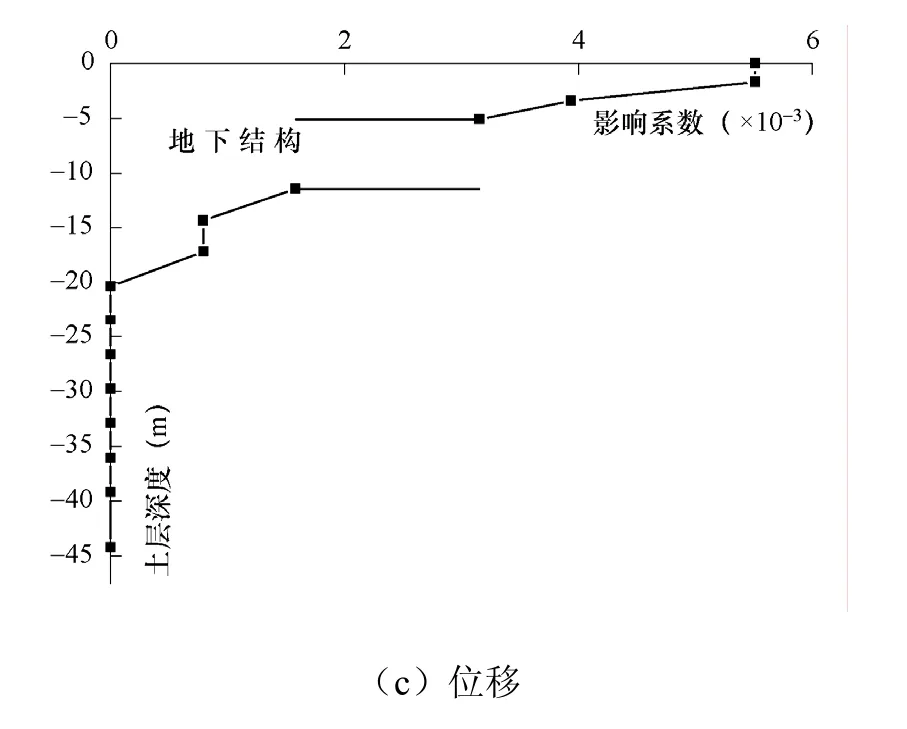
图8 地下结构对中心线上土层节点运动状态的影响系数Fig. 8 Influence coefficient of underground structure to the motion of nodes on central line

从图8可以看出，地下结构存在对中心线上土体节点的速度峰值和位移峰值的影响分别不足2%和1%，可不考虑地下结构的影响。总的来看，地下结构的存在增大了结构上部土层的加速度峰值，同时却减小了其下部土层的加速度峰值，最大增幅和最大减幅分别为6.7%和2.3%。在上部土层中，土体节点的加速度峰值随着土层深度的增大而先增大后减小，而土层节点P3处的加速度峰值所受影响最大，图9给出了节点P3的运动状态时程。

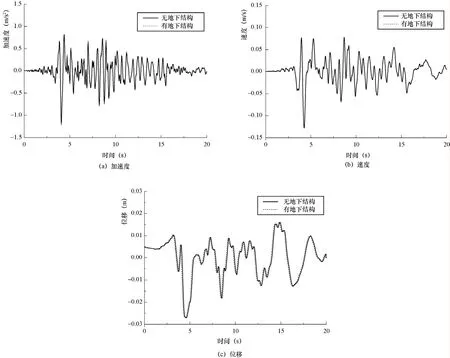
图9 节点P3处运动状态时程Fig. 9 Motion time history of node P3

2.3 地下结构对轴线1上土层节点运动状态的影响

在一致地震动作用下，地下结构对轴线1上土层节点的位移峰值、速度峰值和加速度峰值的影响系数如图10所示。

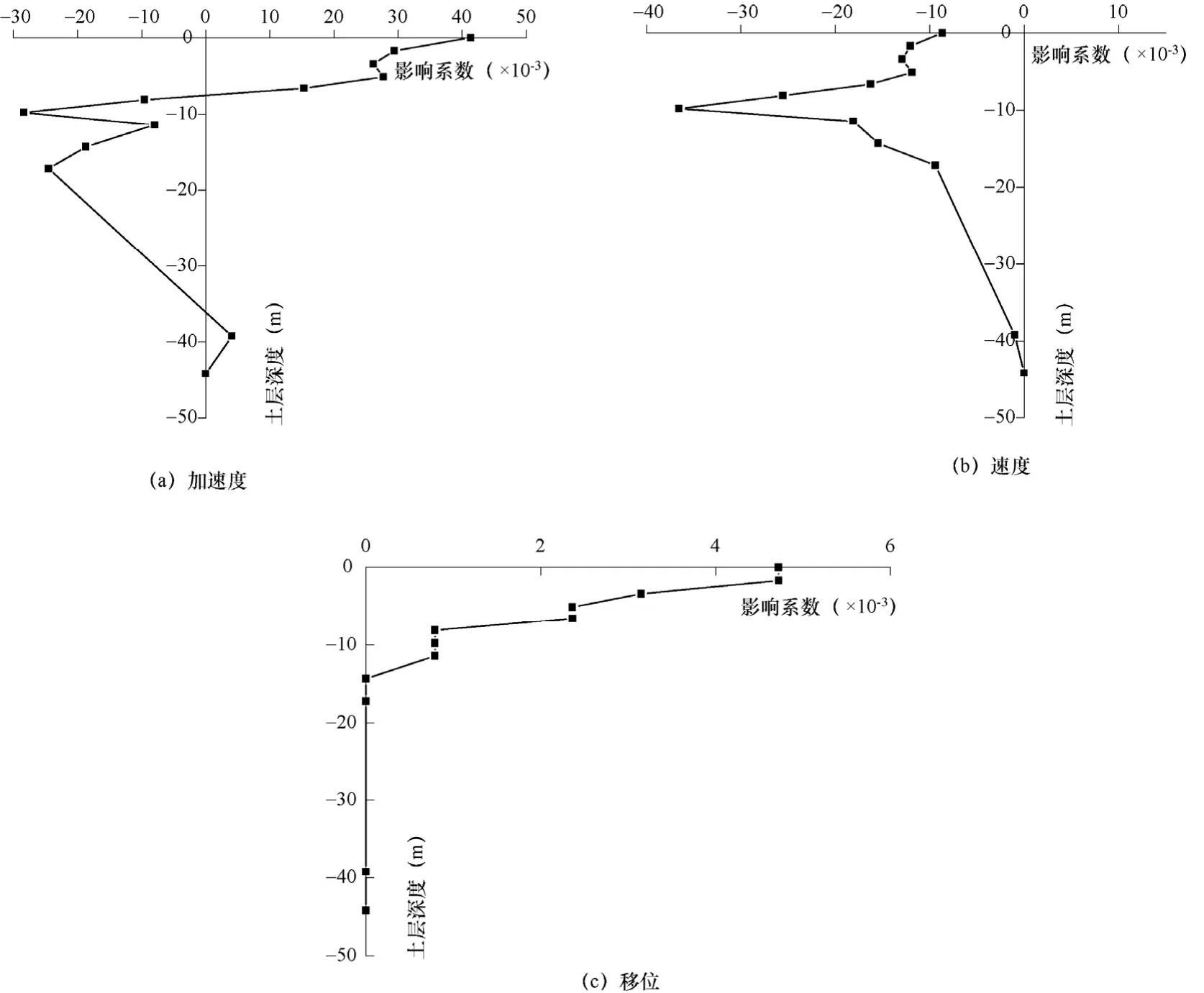
图10 地下结构对轴线1上土层节点运动状态的影响系数Fig. 10 Influence coefficient of underground structure to the motion of nodes on axial line 1

从图10可以看出，地下结构对轴线1（地下结构边缘处）上土层节点的加速度峰值和位移峰值的影响基本上是随着土层深度的增大而减小，而对速度峰值的影响则随着土层深度的增大而先增大后减小。地表的加速度峰值受到的影响最大，增大略大于4%。

3 土层厚度的影响

在其他条件不变的情况下，本文将神户地铁车站所在场地改为上海场地，由此探讨土层厚度对地下结构的影响。表2为上海场地土层的物理参数。

表2 上海场地土层的物理参数Table 2 Physical parameters of soil site in Shanghai

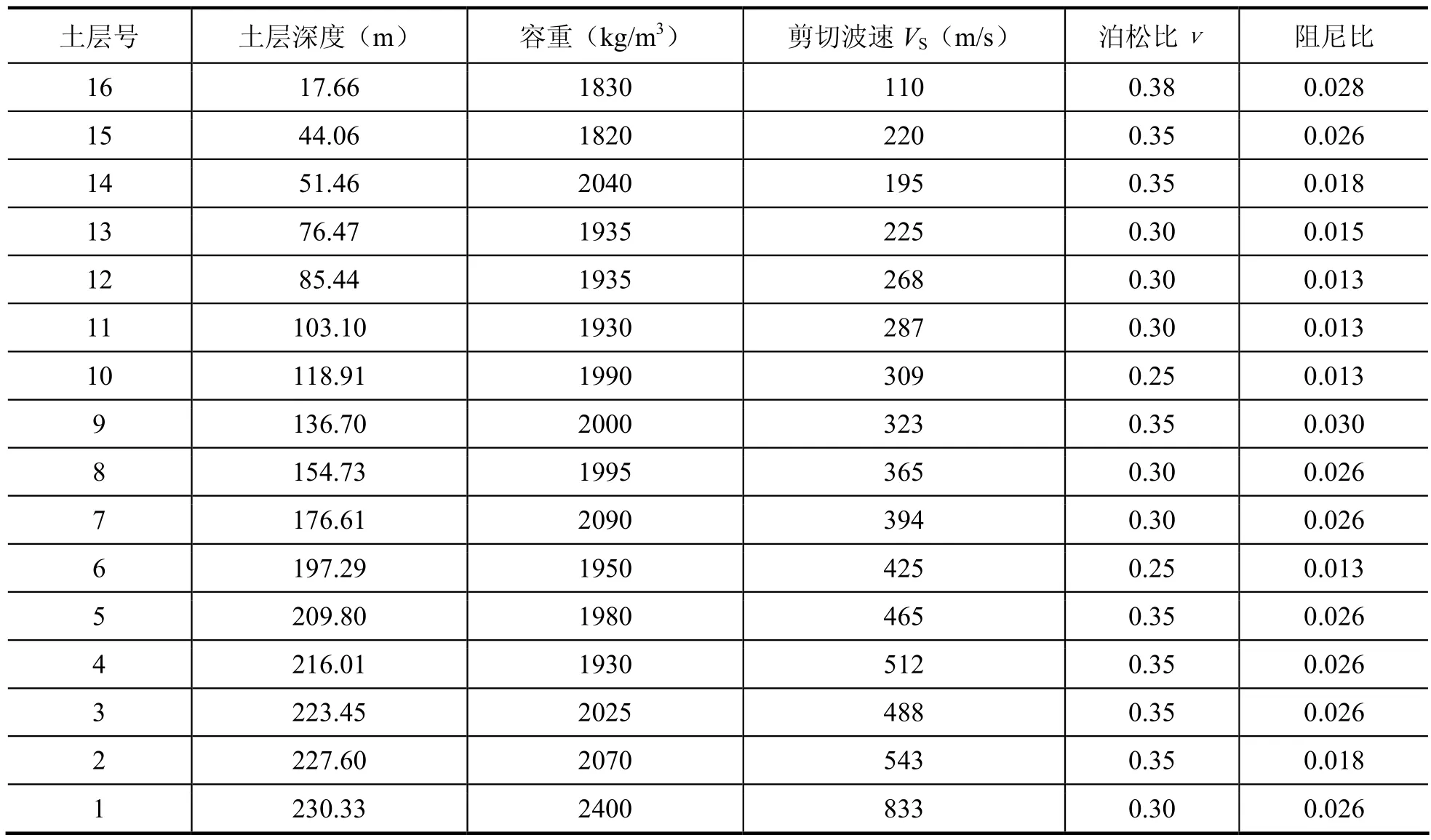
续表

在一致地震动作用下，地下结构对地表上的土层节点的水平位移峰值、速度峰值和加速度峰值的影响系数如图11所示。

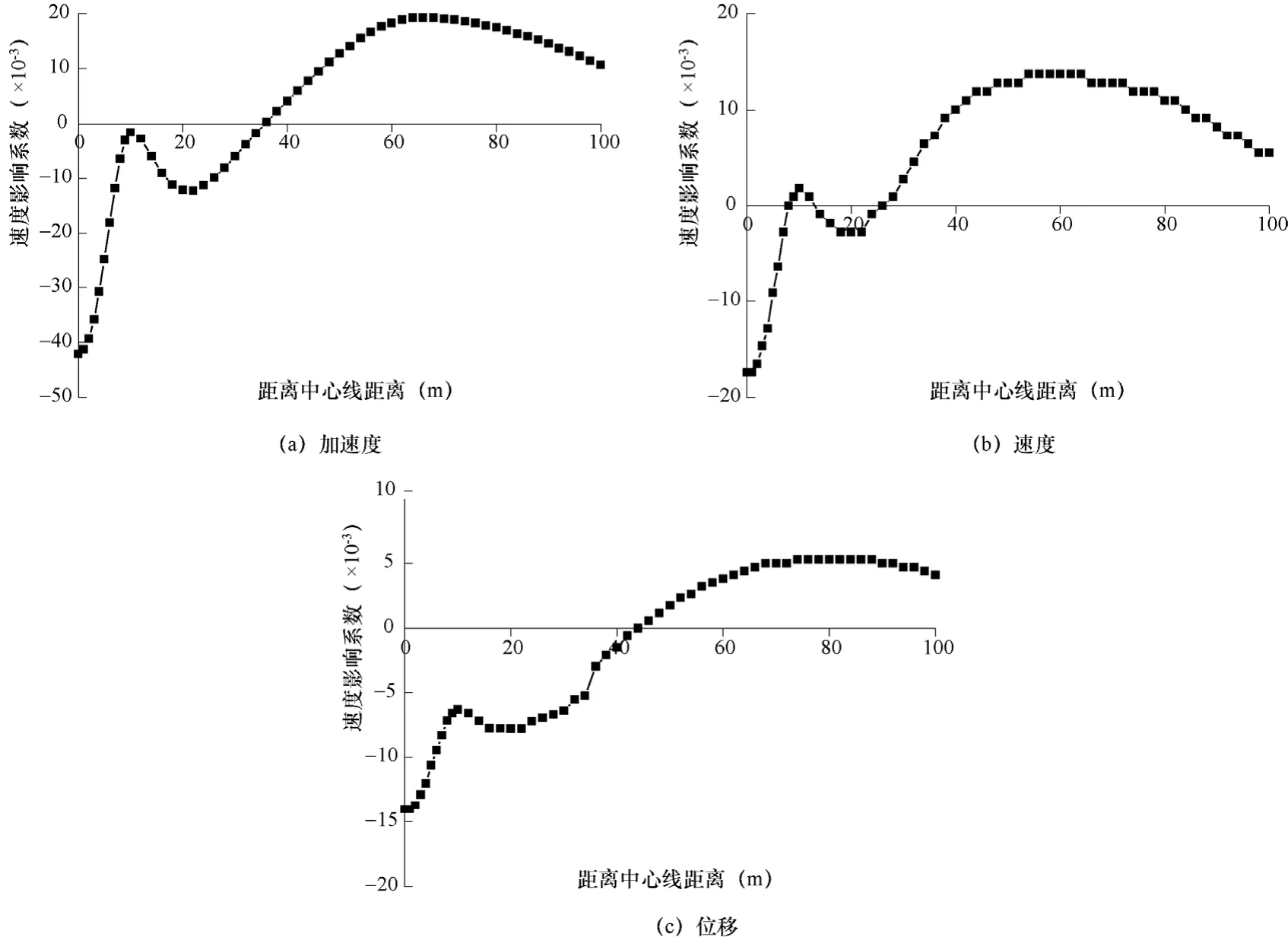
图11 地下结构对地表线运动状态的影响系数Fig. 11 Influence coefficient of underground structure to the motion of ground surface line

从图11可以看出，地下结构的存在对地表的速度峰值和位移峰值影响很小，影响系数分别不足2%和1%。总的看来，地下结构的存在减小了结构周围土体节点的加速度峰值，其中地下结构正上方的地表处减幅最大，为4.2%。随着离开地下结构中心线距离的增加，地下结构减小地表加速度峰值的影响逐渐减小，在距离中心线40m外，地下结构增大了地表的加速度峰值，最大增幅不足2%。

4 结论

（1）在一致地震动输入模式下，当场地土层厚度较小时，日本神户大开地铁站的存在增大了结构上方地表的加速度峰值，但是增大幅度较小，最大增幅为 5%左右；而当场地土层厚度较大时，地下结构的存在却减小了其上方地表的加速度峰值，但减小幅度不大，最大减幅为4%左右。

（2）在场地土层厚度不同但其他条件相同的情况下，地下结构的存在对工程场地地震动场的影响有较大的差别，具体影响大小与土层厚度关系还有待进一步研究。

匡志平，刘竹钊，曹国安，2002. 地下结构纵向随机地震响应和极值分析. 同济大学学报，34（8）：922—926.

楼梦麟，潘旦光，范立础，2003. 土层地震反应分析中侧向人工边界的影响. 同济大学学报，31（7）：757—761.

钱七虎，2000. 现代城市地下空间开发利用技术及其发展趋势. 铁道建筑技术，（5）：1—5.

钱七虎，1999. 岩土工程的第四次浪潮. 地下空间，19（4）：267—272.

杨林德，季倩倩，郑永来，2003. 软土地铁车站结构的振动台模型试验. 现代隧道技术，40（1）：7—11.

庄海洋，程绍革，陈国兴，2008. 阪神地震中大开地铁车站震害机制数值仿真分析. 岩土力学，29（1）：245—250.

Jun Seong Choi，Jong She Lee，2002. Nonlinear earthquake response analysis of 2-Dunderground structures with soil-structure interaction including separation and sliding at interface. See：15th ASCE Engineering Mechanics Conference. New York：Columbia University.

Influence of Underground Structures on Ground Motion Field of Engineering Site

Zhu Xiaoqiao, Lou Menglin and Kong Xianghai
(State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

Taking a subway station in Kobe city, Japan as the engineering example, we establish 2-dimensional finite element models of soil site in natural condition and with underground structure respectivelly. Then, seismic responses of two models were computed under excitations of uniform seismic wave. At last, by comparing difference between the dynamic responses of two models, influence of the underground structure on ground motion field of the site was discussed. The numerical results show that existence of Daikai subway station has influence on seismic responses of adjacent area of the soil to the underground structure, but such influence is limited.

Underground structure；Uniform excitation；Engineering site；Ground motion field

朱小乔，楼梦麟，孔祥海，2011. 地下结构对工程场地地震动场的影响. 震灾防御技术，6（1）：49—58.

上海市科委基础研究重点项目（编号：07JC14051）资助

2010-07-26

朱小乔，男，生于1985年。同济大学土木工程学院硕士生。主要研究方向：防灾减灾工程。E-mail：zhxiaoqiao@163.com

楼梦麟，男，生于1947年。同济大学教授，工学博士。主要研究方向：工程结构抗震与防灾。