基于曲线波隐马尔可夫模型的人脸检测*

王吉林，叶建隆，赵 力，邹采荣(1．盐城工学院，信息工程学院，江苏盐城4051;)．东南大学信息科学与工程学院，南京10096

人脸检测［1］是指对图像和视频中的人脸做出正确的定位，在自动人脸识别系统中，人脸检测是其第一个关键的步骤，因为人脸识别的精度与人脸检测的精度息息相关。近些年来，人脸检测技术已经成为人们研究的热点之一，是广大研究人员公认的难题。这一问题的难度主要表现在三个方面［2］:①虽然每张人脸都有眼睛、鼻子和嘴，且都按照一定的空间结构分布，但人与人之间的五官差异较大，导致反映在图像中纹理的不同;②人脸的一些非固定特征，如眼镜、胡子等，也使人脸检测变得复杂;③由于人脸是一个三维非刚性物体，所以光照条件的不同，也使得人脸图像千变万化。总之，人脸的千姿百态，使得人脸检测变得十分困难。

尽管如此，人们还是提出了许多有效的人脸检测方法［3－6］，Rowley等提出了基于多个神经网络综合决策的人脸检测方法［7］，该方法在理论上可以通过大量样本的训练来检测不同角度、不同遮挡、不同脸型的人脸，但其训练样本，尤其是非人脸样本的选择和神经网络的收敛都是非常困难的问题;Viola等提出了一种基于Adaboost的人脸检测算法［8］，有效地解决了检测速度问题，且具有较好的检测效果，但是存在着训练速度缓慢、检测结果过分依赖训练样本的现象;刘伟等提出了基于Gabor小波和神经网络的人脸检测方法［9］，一定程度上改善了检测效果，但由于Gabor小波的有限方向性及神经网络计算复杂性，并不适合实时处理;曹刚等提出了用小波变换域中的小波系数作为隐马尔克夫模型人脸检测的观察特征向量［10］，取得较好的实际效果，但是小波只能捕捉具有点奇异的函数，并不能很好地描述人脸面部及五官的边缘特征，即不是图像的“最稀疏”表示，对人脸检测结果产生了较大影响。

本文在曹刚等人的基础上，将人脸图像的曲线波变换系数作为观察特征向量，然后根据隐马尔可夫模型对人脸拓扑结构的约束以及曲线波变换的多尺度性和良好的方向性，采用曲线波隐马尔可夫模型(Curvelet Hidden Markov Model，CHMM)从粗尺度到细尺度的人脸检测，大大地提高了人脸检测的效果。实验结果表明，该方法相对于基于小波隐马尔可夫模型人脸检测，具有更高的检测速度、正确率和鲁棒性。

1 Curvelet变换的定义

小波是一个很好的函数分析工具，在二维或多维情况下，因为其有限的方向性(即个向同性)，由一维小波张成的可分离小波并不能“最优逼近”具有线或者面奇异的函数。对于一般的目标函数(如人脸图像)，边缘是面部轮廓及五官的不连续所在，通常情况下，边缘并不是点状和直线型的。对于一个具有曲线奇异性的目标函数来说，小波并不是最稀疏的表示方法。

Curvelet变换［11］正是为了克服小波的这一局限性而产生的。与小波变换不同，除了尺度和位移参数外，Curvelet还增加了一个方向参数，使之具有更好的方向辨识能力。因此，Curvelet对图像的边缘，如曲线、直线等几何特征的表达更加优于小波，使用Curvelet变换提取人脸特征是一条更有效的途径。2005年Candes等对第一代Curvelet算法进行改进，提出了更简单、更便于理解的快速Curvelet变换算法，即第二代Curvelet变换，大大降低了数据的冗余度。

第二代Curvelet变换有两种离散的实现方法，分别是基于非均匀采样的快速傅里叶变换(Unequally-Spaced Fast Fourier Transform，USFFT)以及基于特殊选择的傅里叶采样的卷绕(Wrapping of specially selected Fourier samples，Wrapping)。USFFT和Wrapping这两种方法的主要区别是每个尺度和每个方向上的网格选择方法的不同。

对∀f［m1，n1］∈R2，0m1，n1N，基于 USFFT的Curvelet算法描述如下

(1)将f(m1，n1)进行二维傅里叶变换，得到F(m2，n2)，－ N/2≤m2，n2N/2;

最后，成本管控采用方法落后、工作人员综合素质不足。受到传统思维观念的影响，现如今很多建筑施工企业在成本管控工作中采用的仍旧是传统的方法措施，很多企业甚至未设置专门的成本管控组织，而是用财务人员承担成本管控工作，须知成本管控和财务工作是两个不同的体系，财务人员对成本管控的了解必然存在不足。一部分企业及时建立了专门的成本管控队伍，但是队伍在专业素质上却存在问题，根本无法胜任新时期的成本管控工作。

(2)在 F(m2，n2)中对每一个尺度和角度(j，l)组合再取样(或插值)，得到新的取样函数 F(m2，n2－ m2tanθl)，(m2，n2)∈Pj;

(3)用窗口函数 Uj(m2，n2)乘以新的 F(m2，n2－m2tanθl)可得

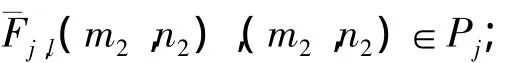
2 基于HMM的人脸建模

隐马尔可夫模型(Hidden Markov Model，HMM)是指用概率统计的方法来描述时变信号过程，最初在语音信号识别中得到了广泛的应用，通常记HMM模型为λ={A，B，π}，其中A为状态转移概率矩阵，B为观察概率矩阵，π为初始状态分布。

HMM是由两种机理构成的随机过程［12］，一个是内在有限状态的马尔可夫链，马尔可夫链按照状态转移概率矩阵改变状态。另一个是序列观察值的集合(或训练集)，其中每个观察值都与马尔可夫链中的一个状态相对应。在实际应用中，由于马尔可夫链中的状态不能直接观察到，只能通过观察序列来推断状态的存在及转移特征，即模型的状态掩盖在观察序列中，所以称之为隐马尔可夫模型［13］。HMM在模式识别应用中的原理是通过从各个类别的样本模板中提取的观察值序列训练其各自的参数λc，c=1，2，…，C，C 是待识别的类别个数，对于输入未知的观察值序列 O={O1，O2，…，OT}，T是观察值序列的向量个数，则该观察值序列的类别c*为:

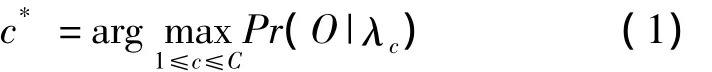
观察值序列O由模式识别中提取的特征值组成，Pr(O|λc)是观察序列O与HMM参数λc的匹配值。

如果是曲线波变换域中提取的特征(如Curvelet系数)组成的观察值序列来构造的HMM就称为曲线波隐马尔可夫模型。

2．1 人脸特征提取

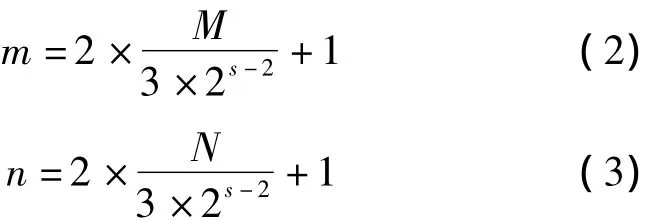
其中，m、n分别为行数和列数，s为Curvelet分解尺度的大小。与小波变换相类似，Curvelet分解层数的大小将直接影响图像特征提取的效果。若分解层数太小，则图像数据量没有很好地压缩，含有较多的冗余信息;若分解层数太大，则丢失了一些图像的基本特征。设原始人脸图像大小为M×N，一般定义Curvelet最大分解层数S为

通过实验可知，公式(4)得到的Curvelet分解层数大小能较好地满足特征提取的需要。对于大小为112×92的人脸图像，通过式(4)计算得到Curvelet分解层数值为4，由式(2)、(3)得到低频系数大小为19×15，由此可知压缩比超过36:1，有效地减少了特征空间的维数和运算量。分解后的高频系数反映图像各个方向的细节、纹理等重要信息。为了计算方便和实际需要，设定每层方向数为8的倍数，第一层8个方向，第二层16个方向。图1所示为人脸图像Curvelet分解过程示意图，图1(a)为原始人脸图像，图1(b)为分解后的低频子带系数，图1(c)为第二层16个方向的高频子带系数。

图1 人脸图像Curvelet分解示意图

2．2 人脸HMM向量的组成

HMM是一种刻画信号统计属性的建模方法，对于人脸这种二维图像而言如果建立二维HMM其计算量会太大［14］。考虑到计算的实时性，我们仍采用传统的一维HMM。人脸HMM的观察值就是从人脸图像的Curvelet变换域中提出的Curvelet系数。人脸图像可以进行不同尺度的Curvelet变换，分解为低频，第1，2…层高频系数，这里我们采用其中的低频系数作为观察值，则OjL={O1，…，Oi，Oi+1，…OT}构成了尺度j=1的低频观察值序列(其中Oi为低频向量)。

2．3 人脸的HMM参数模型及训练

aij表示t时刻从状态si转移到t+1时刻状态sj的概率，即为一阶HMM的状态数。一般来说，N越大HMM描述越精确，但其复杂度越高。考虑到人脸中的眼睛、鼻子和嘴的区域的特征较为稳定，并且为了提高检测速度，我们选取的人脸的N为3，即状态集合S={s1，s2，s3}={眼睛、鼻子、嘴}，如图2所示。

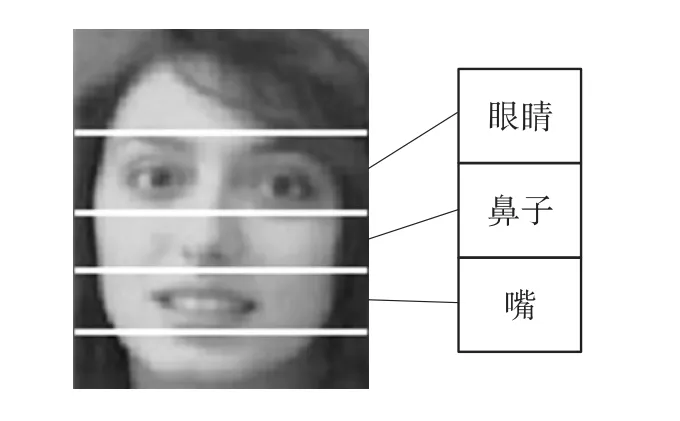
图2 HMM状态示意图

(2)观察值概率矩阵B={bj(k)}，设t时刻状态sj的观察值为 vk，即 bj(k)=Pr(ot=vk/qt=sj)，1≤k≤M，1≤j≤N，M和N分别观察数和状态数。bj(k)与时刻t无关，而只与当前的状态j有关，所有的bj(k)组成了大小为N×M的观察矩阵B。

(3)初始状态概率矩阵π，设HMM的起始时刻t=1，π1=Pr(q1=s1)表示t=1起始状态为s1的概率，则 π =(π1，π2，…，πN)表示起始时刻为各种可能状态S=(s1，s2，…，sN)的概率。由上述分析可知，，即初始状态只可能是所有状态的一种且所有可能的初始状态概率之和为1。

3 基于CHMM的人脸检测

人脸检测是指在输入图像中确定是否有人脸存在，如果有则确定其位置、大小的过程。本文提出的检测方法需要用人脸的标准模板CHMM参数进行检测，由于各个人脸样本的尺度和灰度分布各不相同，需先对他们进行尺度和灰度分布标准化，然后将所有样本取灰度平均并压缩到需要尺度作为标准模板。根据Curvelet变换的多尺度性，我们采用尺度从粗到细的搜索策略，在此先介绍基于单尺度的CHMM的人脸检测。

3．1 基于单尺度CHMM的人脸检测

基于单尺度的CHMM的人脸检测是用标准模板某个尺度为j的CHMM参数λjL分别在输入图像的Curvelet变换域对应尺度下的系数矩阵中进行匹配搜索。首先在每个检测点上取得以该点为左上角的矩形框，使该矩形框的大小与标准模板的Curvelet变换域中对应尺度的低频系数矩阵大小一致，再在矩形框中提取观察序列值}，然后用Viterbi算法计算该检测点，计算完该点对应的后，然后再将检测范围中再从上到下、从左到右以此逐点计算各个检测点对应的Pr。设在检测范围中检测的点数为M，则搜索完毕可得M个Pr(OjL［k］|λjw)，1≤k≤M。

若已知输入图像含有单个人脸，可以根据

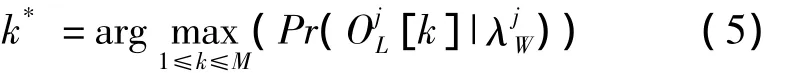
式中k*为所有监测点中为最大的检测点，即单个人脸对应的位置。若输入图像含有多个人脸，可以根据下式判定:

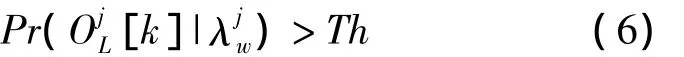
3．2 基于多尺度CHMM的人脸检测

为了进一步提高检测精度，根据Curvelet变换的多尺度特性，我们采取尺度从粗到细的搜索策略，即先用标准模板粗尺度Curvelet系数的CHMM参数在输入图像粗尺度的Curvelet域按3．1中的方法进行全局范围检测，取得人脸的大致位置，再根据人脸的大致位置，用CHMM标准模板作为细尺度上的Curvelet系数，将输入图像的细尺度系数在Curvelet域中用同样的方法进行局部检测，取得人脸的精确位置。

4 实验结果及分析

为了验证算法的有效性，本文实验采用的是一套BioID样本训练人脸库，该人脸库共有23个人共计1 521幅人脸图像，每幅图像为384×286的灰度像素，具备不同的光照条件、背景、表情、发型和有无眼镜等，并且人脸有一定的侧转角度。评价检测结果的有效性包括两个方面，检测率和检测速度。人脸检测率为给定图像中检测出来的人脸和人脸总数的比率，检测速度是检测人脸所需的时间。

实验采用Pentium 4 3．0 GHz，2 GB内存的计算机。为了验证算法的快速性以及对样本随机选取的鲁棒性，先在BioID人脸库中随机选择1 000幅人脸图像，像素统一调整到112×92，再有代表性地选取1 500幅非人脸图像，大小也为112×92，这2 500个图像样本形成初始的训练库。最后对500幅人脸图像进行检测，部分复杂检测图像的检测结果如图3所示，将本文的算法和基于小波隐马尔可夫模型方法结果进行比较，表1给出了两种方法对待检测人脸的检测正确率及检测速度。

图3 部分复杂检测图像的检测结果

表1 本文算法与小波隐马尔可夫方法的检测结果比较

表中WHMM为基于小波变换隐马尔可夫模型检测方法，CHMM为本文所提出的方法。由表1可以看出，本文算法在BioID人脸数据库上，检测的正确率达到95．42%。相比小波方法，本文算法具有较高的检测率，且特征维数少，检测速度快。无论是简单特征简单背景的人脸图像还是复杂表情复杂背景的人脸图像，本文提出的检测方法都有比较好的检测结果，且受光照和背景影响较小，证明了该方法的鲁棒性。但是本文所训练的参数集是基于Curvelet低频系数，会损失一部分细节和纹理信息，如果将低频子带系数和选择性加上高频子带系数，会带来更好的检测效果。

5 结束语

Curvelet变换由于能充分描述二维图像中的曲线或直线状边缘特征，为图像特征提取提供了一条新途径。该算法通过对人脸图像进行Curvelet变换得到对应的低频和高频分量，并根据各自分量的特点进行人脸特征提取，然后根据隐马尔可夫模型对人脸拓扑结构的约束，采用3状态的隐马尔可夫模型进行从粗到细的人脸检测。以BioID人脸库为实验数据，结果表明，本文方法特征提取合理，检测率较高，对于人脸光照、姿态以及表情变化具有良好的鲁棒性。下一步工作是将训练集由低频子带系数有选择性加一些高频子带系数，并考虑二维隐马尔可夫模型来进行参数集训练，以进一步提高检测率。

［1］ 吴暾华，周昌乐．平面旋转人脸检测与特征定位方法研究［J］．电子学报，2007，35(9):1715 －1718．

［2］ Sung Kah-Kay．Learning and Example Selection for Object and Pattern Detection．Ph．D．thesis，MIT AI Lab，January，1996．

［3］ 吴证，周越，杜春华，等．彩色图像人脸特征点定位算法研究［J］．电子学报，2006，36(2):309 －311．

［4］ Yang Mingshuan，Driegman David J．Detecting Faces in Images:A Survey［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24(1):34 －58．

［5］ Goldmann L，Monich U J，Sikora T．Components and Their Topology for Robust Face Detection in the Presence of Partial Occlusions［J］．IEEE Transactions on Information Forensics and Security，2007，3(2):559 －569．

［6］ Sznitman R，Jedynak．Active Testing for Face Detection and Localization［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32(10):1914 －1920．

［7］ Rowley H A，Baluja S，Kanade T．Neural Network Based Face Detection［J］．IEEE Trans Pattern Analysis and Machine Intelligence，1998，20(1):23 －38．

［8］ Viola P，Jones M．Robust Real-Time Face Detection［J］．International Journal of Computer Vision，2004，57(2):137 －154．

［9］ 刘伟，朱浩，刘吉邦，等．基于Gabor小波和神经网的人脸检测［J］．通信技术，2009，42(2):191 －193．

［10］曹刚，游志胜，刘直芳．基于小波隐性马尔可夫模型的人脸检测［J］．信号处理，2004，20(1):26 －29．

［11］ Candès E J，Donoho D L．Curvelets［D］．PaloAltoDepart-ment of Statics，Stanford University，1999．

［12］陈茂林，陈飞虎．自组织隐马尔可夫模型的人脸检测研究［J］．计算机学报，2002，25(11):1165 －1169．

［13］朱明，郭春生．隐马尔可夫模型及其最新应用与发展［J］．计算机系统应用，2010，19(7):255 －257．

［14］周顺先，林亚平，王耀南，等．基于二阶隐马尔可夫模型的文本信息抽取［J］，电子学报，2007，35(11):2226 －2231．