食饵—捕食者模型

李娟

(德州职业技术学院 计算机信息工程系，山东 德州 253034;)

0 引言

自然界中同一环境下的两个种群之间存在着几种不同的生存方式，比如相互竞争，即争夺同样的食物来源，造成一个种群趋于灭绝，而另一个趋向环境资源容许的最大容量;或者相互依存，即彼此提供部分食物资源，二者和平共处，趋于一种平衡状态;再有一种关系可称之为弱肉强食，即某个种群靠丰富的自然资源生存，称为食饵(prey)，而另一种群靠捕食食饵为生，称为捕食者(predator)，二者组成食饵——捕食者系统．海洋中的食用鱼和软骨鱼(鲨鱼等)，美洲兔和山猫，落叶松和蚜虫等都是这种生存方式的典型．食饵和捕食者的数量是如何演变的呢?近百年来许多数学家和生态学家对这一系统进行了深入的研究，建立了一系列数学模型，这里先介绍的是最初的，最简单的一个模型，它是意大利数学家volterra在上个世纪20年代建立的．

1 volterra模 型

用x(t)表示时刻t食饵(如食用鱼)的密度，即一定区域内的数量，y(t)表示捕食者(如鲨鱼)的密度．假设食饵独立生存时的(相对)增长率为常数而捕食者的存在使食饵的增长率减小，设减小量与捕食者密度成正比，比例系数为

捕食者离开食饵无法生存，设它读独自存在时死亡率为常数d＞0，即而食饵的存在为捕食者提供了食物，使捕食者的死亡率减小，设减小量与食饵密度成正比，比例系数为b＞0，则实际上，当 b ×x＞d时，捕食者密度将增长．×y．

给定食饵和捕食者密度的初始值x0，y0，由上可知x(t)，y(t)满足以下方程:

(1)的解x(t)，y(t)描述了食饵和捕食者密度随时间的演变过程．但是我们同样得不到x(t)，y(t)的解析解，需要用数值算法求解．

2 模型的稳定性测试

改变初值x0，y0，分析结果的改变状况，并画出对应相图比较．原shier．m文件不变，编程中其它不变，只将初值条件改变如下:

然后得结果数据，且有相对应的图，一为x(t)，y(t)图，一为y(x)图．如下:

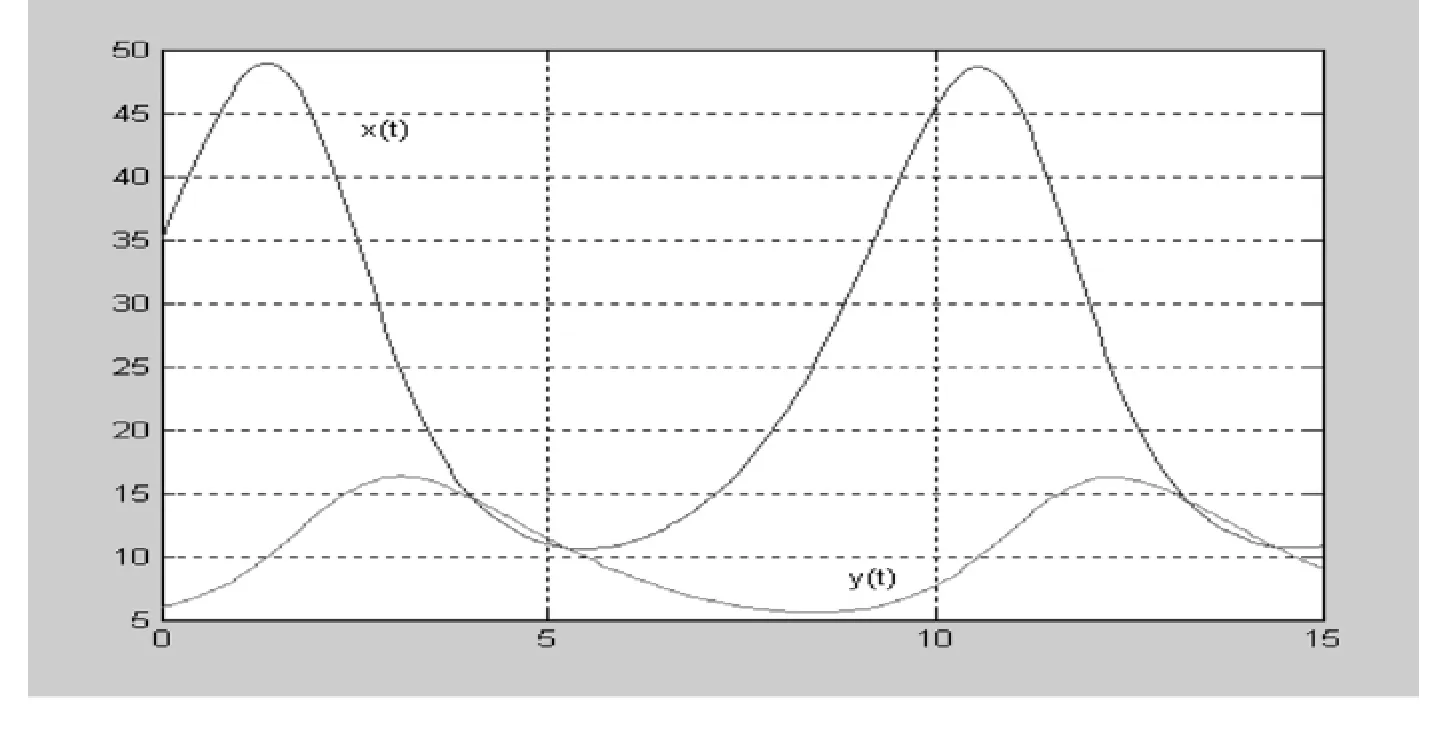
图1 x，y关于时间t的函数图像且初值已经改变Fig．1 x，y about time t function image and initial value has been changed

图2 y关于x的函数图像且初值已经改变Fig．2 Y about x function image and initial value has been changed

在仅改变初值的情况下，图形的整体走势没有多大改变，且周期性也保持着．这说明volterra模型设计较为合理，下面改变模型中系列参数的值，试看参数值对模型影响程度的大小．

首先建立shierpp．m文件，其编程为:

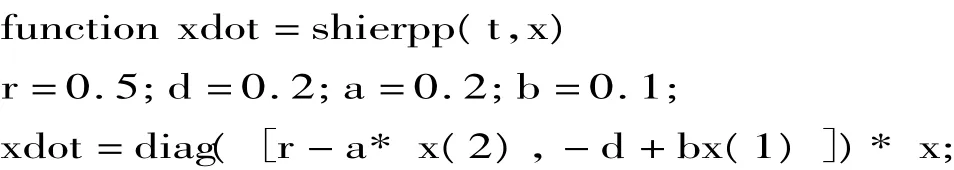
在运行程序中调用龙格——库塔公式时将shier．m文件名改为shierpp．m文件名:

然后得到结果对应的图:

图3 x，y关于时间t的函数图像且系列参数值已经改变Fig．3 x，y about time t function image and series parameter values have changed

图4 y关于x的函数图像且系列参数值已经改变Fig．4 y about x function image and series parameter values have changed

由上图与原图比较可看出，当参数值改变较大时，对volterra模型影响较大．其中最明显的一点就是:改变了食饵——捕食者系统的周期性．在这种破坏了周期性条件下的食饵——捕食者系统会出现某群种灭绝的情况，这是我们不愿看到的，于是我们必须在构造符合实际的数学模型时考虑合理参数值的选定．

3 常数投放并常数捕获且具功能反应食饵——捕食者系统模型

其中所含参数r，a，d，b与volterra模型中所代表含义一样，并添进参数k与h，其中k表示定期投放食饵的量，h表示定期捕获捕食者的量．以volterra模型为参考得下列方程:

先利用数值算法求解，其编程过程与建立volterra模型时相似．

3．1 模型的数值解

为进一步显示出此模型的优越性，我们选择参数值为r=0．5;d=0．2;a=0．2;b=0．1;编程步骤为:

首先建立shierpp．m文件:

然后在运行程序中调用龙格——库塔公式时将shier．m文件名改为shierppii．m文件名，并将ts最大值设为10，操作如下:

然后得到结果对应的图:

由上两图可知，虽在参数值不太合理的情况下，模型(2)依然体现出系统的周期性，而且值随时间的变化依然保持良好的连续性，所以此模型建立得较为成功．

4 模型的探讨

通过对模型(1)的初值、所含参数的改动以及在此基础上建立新的模型(2)，并相互比较稳定性、周期性的变化，从中我们可以得到一些经验:构造一个好的模型，第一点其要与实际相符，能真实的反应客观现象;其次就是变量的初始值要选择恰当，所含参数要尽量合乎情理;再次是再建立好一个认为比较合理的模型后，要思考并猜测每次测试结果与现实真值有所差异的原因，然后引进下一个参数或改变变量之间简单的关联公式．

图5 x，y关于时间t的函数图像且依据模型(2)得出Fig．5 x，y about time t function image and based on model(2)draw

图6 y关于x的函数图像且依据模型(2)得出Fig．6 Y about x function image and based on model(2)draw

［1］郭见军，贺昌政．竞争系统两种群捕获的生物经济最优控制问题［J］．西南工学院学报，2002，17．

［2］马知恩．种群生态学的数学建模与研究［M］．合肥:安徽教育出版社，1994．

［3］程荣福，蔡淑云．一类具功能反应的食饵—捕食者两种群模型的定性分析［J］，生物数学学报，2002，17．

［4］张芷芬，丁同仁，黄文灶等．微分方程定性理论［M］．北京:科学出版社，1985．

［5］张锦炎，冯贝叶．常微分方程几何理论与分支问题［M］．北京:北京大学出版社，2002．