白龟山水库洪水预报误差分布规律分析

田 力

（河南省白龟山水库灌溉工程管理局，河南 平顶山市 467031）

1 流域概况

白龟山水库位于淮河流域沙颍河水系沙河本干上。是一座大（Ⅱ）型水库，以防洪为主，兼顾灌溉、供水、养鱼等综合利用。控制流域面积2 740km2，它与上游昭平台水库形成梯级水库，区间流域面积1 310km2。水库下游有平顶山、漯河、周口等重要城市和京珠高速、京广铁路及107国道。漯河以下为豫皖平原，地理位置极为重要。

目前，水库洪水预报模型和方法的研究已经比较成熟，预报方案的精度评定也有相应规范，但对洪水预报误差分布特性的研究不多。已有的方法主要是采用正态分布或对数正态分布来描述，对于一次降雨径流过程，在不发生决堤等灾害的情况下，模型预报误差是随着降雨增大而逐渐趋于稳定，控制在一个有限的区域内。因为当流域下垫面达到饱和后，所有降雨全部产流，预报净雨量与实际净雨量基本相等。而正态分布的两端是趋于无穷大的，在实际洪水预报操作中发现直接用其描述洪水预报误差分布规律是欠合理的。为此，建立了基于极大熵洪水预报误差分布的模型，通过白龟山水库历史洪水的预报误差样本序列，分析其模型预报误差的分布规律。

2 洪水预报误差分布的极大熵模型建立

熵增原理在信息熵领域则叫做“极大熵原理”。按照极大熵准则，在不确定性问题的所有可行解中，应该选择在一定约束下使得熵（或条件熵）能达到极大化的一个解，即对数据的内插或外推采取最客观的态度。而熵最大就意味着获得的总信息量最少，即所添加的信息量最少，因为数据不足而做的人为假定也（人为添加信息）最小，从而所获得的解是最合乎自然、偏差最小的。

水文水资源学科从本质上看，是一门有关水信息（采集、传输、整理、分析、应用）的学科，其中存在着许多不确定性问题[1]，极大熵原理是一种有效的解决途径。国内外许多学者曾将极大熵原理应用到水文频率分析、径流对降雨的条件分布等[2～3]问题中，但在预报误差分布规律方面研究的不多。

对于洪水总量的预报误差，其分布特性是与已知误差信息有关的。由于无法通过概率论理论直接推导出误差变量的先验分布，误差数据又十分有限，因此是一个典型的不确定性问题。只能依据有限的历史洪水预报误差序列，推求一种概率分布，使它和已有历史洪水预报误差的信息基本一致，并且没有太大误差，极大熵准则正好可以有效地解决这个问题。

就一场洪水而言，洪水总量预报误差或正或负，对多次洪水，则可以将模型的预报误差限定在一个有限区域（-a，a）内。设预报误差变量为x，其概率密度函数为f（x），在区域（-a，a）内，误差分布应满足一般概率分布的约束式（2）。同时由于误差为确定数值，所以样本的各阶原点距也是存在的，即应当满足约束式（3）。则最终建立的误差分布极大熵模型为：

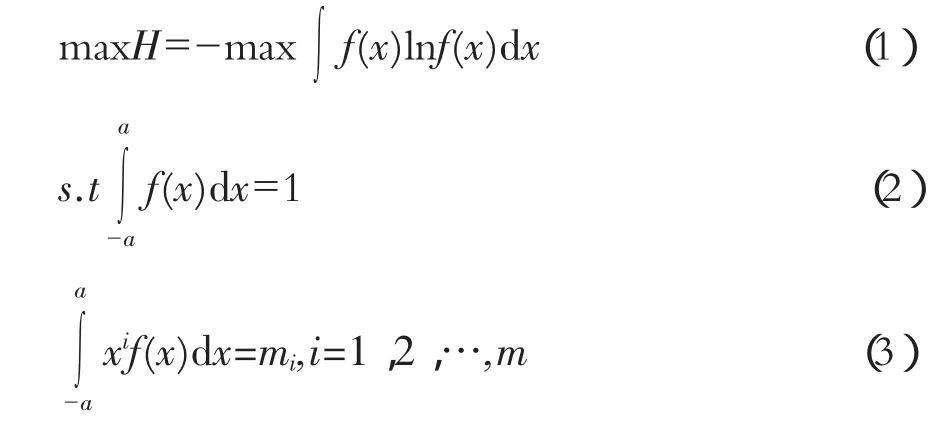
式中m为所用矩的阶数，为第i阶原点矩。

3 洪水预报误差分布的极大熵模型求解

上述模型的求解是一个泛函条件极值问题。为了求得f（x）的表达式，根据变分法引入拉格朗日乘子λ0，λ1，…，λm，设J为拉格朗日函数，R表示积分区域［-a，a］，则

要使函数J达到极值，令导数dJ/df（x）等于零，解之得

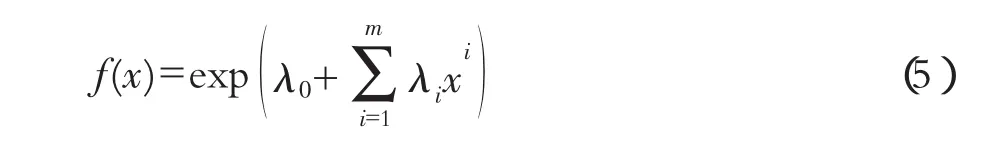
式（5）即为洪水总量预报误差的概率密度函数解析形式，只要确定其中的参数λ，就可以完全确定函数f（x），文献[4]也给出了参数λ的具体求解方法。将式（5）代入约束条件式（2），可解得

将式（6）代λi求导，得

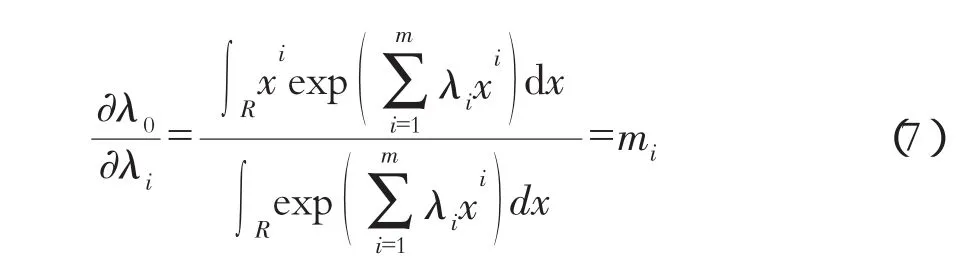
通过式（7）可建立求解λ1，λ2，…，λm的m个方程组，求出λ1，λ2，…，λm后，可根据式（6）求出λ0。但由于式（7）是一个二元非线性方程组，目前没有解析解法，而且存在多解现象，几何意义是几张曲面在空间相交的公共点。因此将式（7）转换为一个非线性优化问题，令

4 计算结果

根据表1的模拟预报结果，计算产流预报误差序列的1阶、2阶和3阶原点矩，分别为m1，m2，m3。将其带入式（8），得到3个残差方程

另外，极大熵分布与指数的理论分布（以指数分布为例）概率密度函数曲线，如图1所示，两者已基本重合。从图1中可以看出，极大熵分布已对理论分布做出了较好逼近。由此可以看出，根据样本数据，利用极大熵模型求解概率分布是可行的，精度也相对比较高。

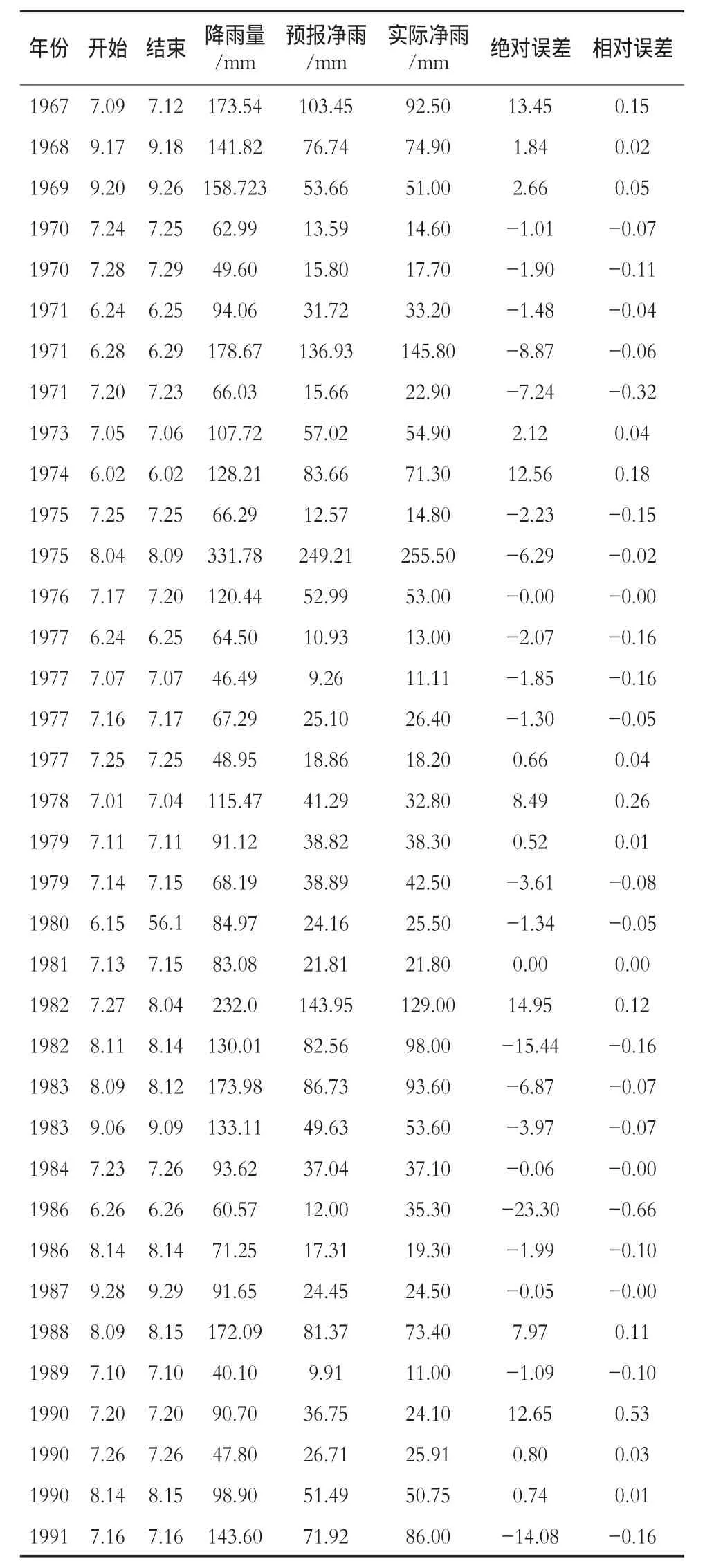
表1 白龟山水库场次洪水模拟结果

表2 白龟山水库不同预报误差上限对应结果

图1 指数分布与极大熵分布概率密度曲线图

研究结果表明：

（1）当误差上限达到一定值时，误差分布则基本保持不变。

（2）极限误差的大小与水库产流模型的预报精度和误差系列有关。预报精度越高，误差就会越小。

（3）白龟山水库的产流方案预报误差极限值为35mm。从表中还可以看出，残差平方和的量级已经很小，能够满足防洪调度的精度要求

上述预报误差分布规律是通过有限的历史洪水数据分析得到的，反映的是流域实际已发生洪水的预报误差分布规律，对应的基本都是中小洪水。对流域从未发生的设计校核等大洪水，当实际降雨量级达到此标准时可能会发生决堤等情况，此时预报误差在趋于稳定后会再增大。但这类洪水多缺乏实际观测资料，因此文中暂不考虑这类情况。

［1］王栋，朱元生.最大熵原理在水文水资源科学中的应用［J］.水科学进展，2001，12（3）：75-80.

［2］李元章，丛树铮.熵及其在水文频率计算中的应用［J］.水文，1985，（1）：22-26.

［3］Sonuga JO.Principle ofmaximum entropy in hydrologic frequency analysis［J］.JHydrol，1972，17：177-191.

［4］李继清，张玉山，王丽萍，纪昌明.应用最大熵原理分析水利工程经济效益的风险[J].水科学进展，2003，14（5）:626-630.