基于联系数a+bi理论的学生综合素质评价方法
王万军
(1.甘肃联合大学电子信息工程学院,甘肃兰州 730000;2.兰州大学信息工程学院,甘肃兰州730030)
基于联系数a+bi理论的学生综合素质评价方法
王万军1,2
(1.甘肃联合大学电子信息工程学院,甘肃兰州 730000;2.兰州大学信息工程学院,甘肃兰州730030)
在学生综合素质评价中,往往受人为主观因素和不确定因素的影响,使评价出现诸多弊端。运用联系数a+bi理论,提出了一种新的学生综合素质评价方法,并建立相应评价模型。该模型方法避免了其他评价方法的弊端,而且能够保证评价的客观、公正。最后通过实例验证了该方法的有效性和正确性。
a+bi理论;联系数;学生综合素质;评价方法
对学生在校的综合素质评价是关系学生毕业、就业、升学及其进一步衡量学生综合评价的一项重要决策,也是现代学校教学的重要内容之一,它对开展现代的正常教学而言是非常重要的。学生的综合素质评价是一项复杂的系统工程,但由于学生不同的家庭背景、民族习惯、年龄差异、身体状况、智力因素及受教育等情况的不同,呈现出很大的个别差异和多元性。对学生综合素质评价要客观、准确是一件不容易的事情,而在实际的评价中由于评价的方法不当及其评价中一些主观人为不确定性等因素的影响,使得对该评价的结果出现一些失真,从而使决策者的判断导致决策错误。目前,有很多学者提出利用诸如模糊数学法、灰色理论方法、数据包络分析方法、BP神经网络方法等评价方法[1],这些方法虽然各有千秋,可以克服部分人为因素干扰和影响,但仍然在一定程度上存在数据运算量大、隶属度或权系数不容易确定、确定的随机性等问题而使评价结果不太准确。为此,笔者试图利用新出现的联系数中a+bi理论[2-3],提出了一种基于联系数a+bi的学生综合素质评价方法,该方法克服了如上几种评价方法的缺陷和不足,并且相比之下,该方法计算简单、易于操作,评价结果客观、准确、可靠。
1 联系数 a+bi理论
联系数理论[2](connection number)是由赵克勤于1989年提出的一个数学分析工具,是一种不确定性理论方法,是把确定与不确定看成一个确定不确定系统,从事物之间联系与转化的同一度(同)、差异度(异)和对立度(反)3个方面刻画事物。其可以用联系数来表示,由联系数进行定量刻画确定不确定系统之间的关系。联系数的表达式如下:

式(1)为三元联系数表达式或同异反联系数表达式,其中a,b,c∈[0,1],a为同一度,b为差异度,c为对立度,i为差异度的系数,并规定其值为[-1,1]之间,因不同情况而定;j表示对立度的系数,规定其值取-1,也可根据情况作为表达式的标志,且a,b,c满足归一化条件,a+b+c=1。
有时根据需要可以进一步简化式(1)为如下表达式:

式(2),式(3),式(4)分别称为同异联系数、异反联系数和同反联系数表达式,它是式(1)的特殊表示,可以根据需要选择不同的联系数来表示。总之,这些都是从确定与不确定的定量方法来描述事物在认识上的不确定性。
在综合评价中,如果对问题本身不讨论同一性、差异性和对立性,而要将评价属性进行联系并分析它们之间的内在关系时,可以采用式(2),式(3),式(4)进行。但式(2)更能体现2个待评价对象之间的统一和同一性的关系。因此,在学生综合素质评价中笔者采用式(2)进行数据处理。
2 联系数a+bi理论的学生综合素质评价方法
联系数a+bi理论的学生综合素质评价的一般步骤和过程如下。
第1步:建立待评学生综合素质评价指标体系。
学生综合素质评价指标体系的建立是进行学生综合评价正确与否的关键,是进行评价的核心和基础。笔者在文献[4]和文献[5]的基础上,结合本校学生的实际情况,提出了如表1所示的学生综合素质评价指标体系。
第2步:建立学生综合素质评价的实际指标矩阵与理想指标矩阵。
将学生综合素质评价指标中第i个学生中第j个指标对应的权值或实际值uij建立实际指标矩阵A:
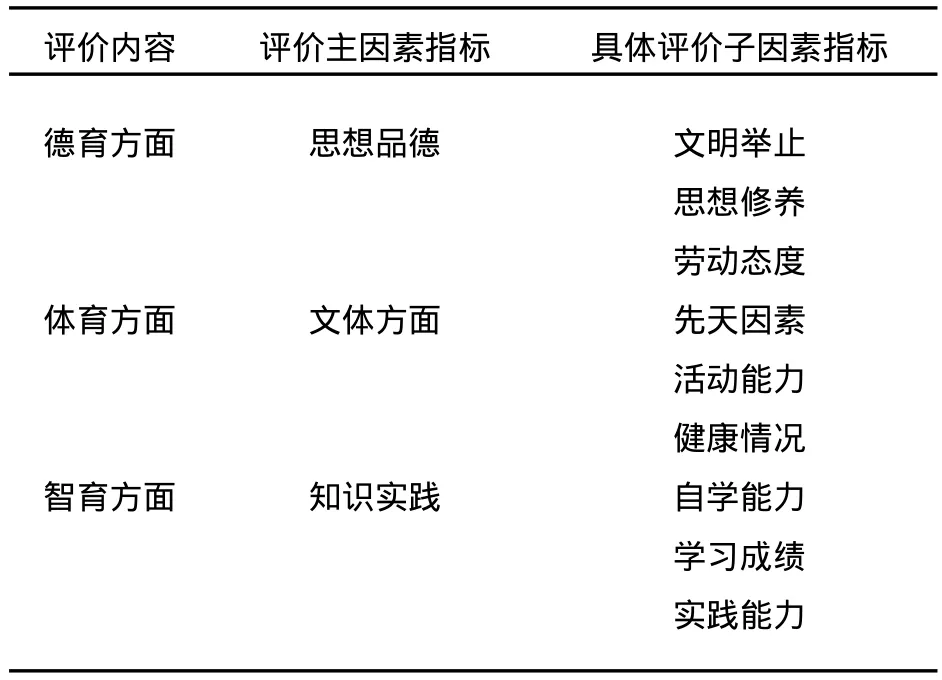
表1 学生综合素质评价指标体系Tab.1 Student comp rehensive quality evaluation system

理想指标矩阵B可以根据实际指标矩阵A进行构造。理想指标矩阵B=[b1,b2,…,bj]中,bj可以根据指标类型值的不同进行处理。通常有成本型和效益型两大类指标。成本型指标是指数值越小越好的指标;而效益型指标是指数值越大越好的指标,对于两类不同的指标,可以采用不同处理方法得到理想指标矩阵B中bj的值。具体计算如下。
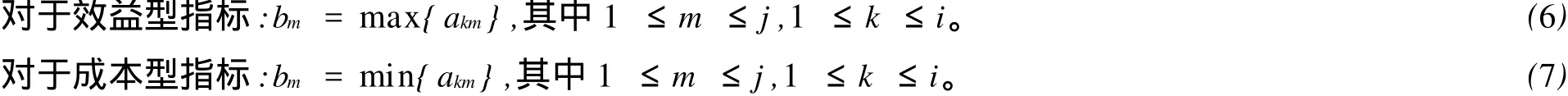
第3步:根据理想指标矩阵B和实际指标矩阵A构成集对(A,B),计算反映综合决策组成的集对(A,B)的联系数a+bi中的同一度系数aij,由同一度系数aij可得到同一度联系矩阵E。

第4步:确定学生综合评价指标的各权值系数矩阵w,常见的有赋权、模糊数学方法、A HP法、专家打分法、理想点方法等等[6-14],当然也有直接给出或确定的权系数。
第5步:确定学生综合评价指标的综合同一度矩阵 R。综合同一度矩阵 R的计算为R=Ew′。(9)
第6步:根据综合同一度矩阵R中各分量值的大小进行排序或择优,分量值越大越优,分量值越小越劣。
3 应用实例与结果比较
某班级现有5名学生进行综合素质测评,各学生的原始数据见表2,就此对5名学生进行综合素质测评并排序。

表2 某班5名学生的原始数据Tab.2 Original data for 5 students
在表2的9个指标中,全为效益型指标。由式(5),式(6)得到实际指标矩阵A和理想指标矩阵B的矩阵分别如下:

利用式(8)计算得到学生综合素质评价的联系数a+bi中a的同一度系数矩阵为

将式(12),式(13)代入式(9),从而计算得到该5名学生的综合素质测评同一度矩阵R中各分量值的大小。

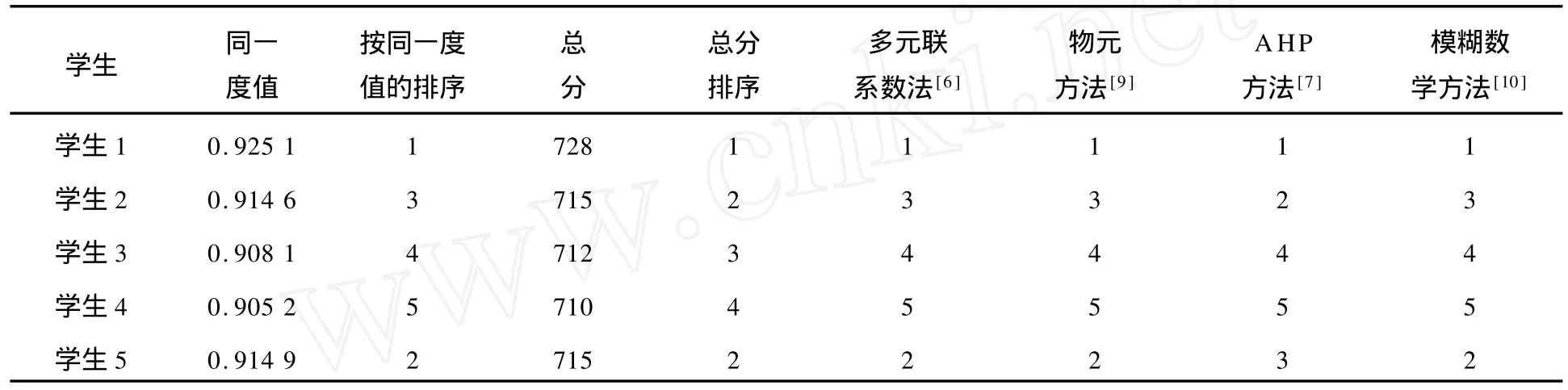
表3 评价排序结果与其他评价方法结果情况比较表Tab.3 Comparison of evaluation sequencing results w ith other evaluation results
从表3分析可知:笔者所提的评价方法与多元联系数法、物元方法、模糊数学方法等的排序结果是一致的,而与AHP方法相比较,学生5与学生2的排序不一致,排序结果不一致的原因是AHP方法在确定或建立决策判断矩阵时会出现主观人为因素的影响,这也就是两种方法排序时产生结果不一致的直接原因。从总分角度考虑,这两个学生的总分是一样的,学生5或学生2谁排前谁排后对决策者来说都是符合实际的,但这却反映不出学生综合素质的本质差距。
4 结 语
将联系数a+bi理论应用到学生综合素质评价决策中,建立了一种新的联系数a+bi评价决策模型,并与其他评价方法进行了比较,说明该方法的评价结果是客观的、有效的和准确的。当然用本文的方法排序比用传统的计算总和或平均值排序稍微复杂,但它却克服了传统方法中总和或平均值相同而无法比较大小的缺陷和不足。该方法能够对学生综合素质进行科学的评价,相对减少了人为因素的影响和干扰,提高了评价结果的客观性、真实性和准确性。
[1]叶义成,柯丽华,黄德育.系统综合评价技术及其应用[M].北京:冶金工业出版社,2006.
[2]赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术出版社,2000.
[3]沈定珠.体育用联系数学[M].北京:中国教育文化出版社,2007.
[4]陆纯宇,陆 云.基于模糊理论的电大学生综合素质评价[J].江苏广播电视大学学报(Journal of Jiangsu Radio and Television University),2006,17(6):51-53.
[5]王万军.区间数排序的一种联系数方法[J].计算机工程与设计(Computer Engineering and Design),2009,30(8):2 055-2 057.
[6]王万军.基于集对分析的学生综合评估及发展趋势预测[J].武汉工程大学学报(Journalof Wuhan Institute of Technology),2009,31(9):78-80.
[7]王万军.基于同异反AHP的综合评价模型研究[J].安徽科技工程学院学报(自然科学版)(Journal of Anhui University of Technology and Science(Natural Science Edition)),2005,20(3):46-49.
[8]王万军.基于同异反区间数排序及其应用[J].洛阳师范学院学报(Journal of Luoyang Normal University),2007,26(2):26-28.
[9]王万军.基于联系数的区间数及其排序[A].中国人工智能[C].北京:北京邮电大学出版社,2007.
[10]王万军.基于集对逻辑的推理[J].甘肃联合大学学报(自然科学版)(Journal of Gansu Education College(Natural Science Edition)),2005,19(3):15-16.
[11]王万军.不确定集对分析探索[J].河北理工大学学报(自然科学版)(Journal of Hebei Polytechnic University(Natural Science Edition)),2008,27(3):67-69.
[12]王万军.基于模糊语言的多属性联系数决策方法[J].数学的实践与认识(Mathematics in Practice and Theory),2008,38(21):54-56.
[13]张 斌,雍歧东,肖芳淳.模糊物元分析[M].北京:石油工业出版社,1997.
[14]肖辞源.工程模糊系统[M].北京:科学出版社,2006.
[15]杨奎河,赵玲玲,周万珍.用模糊数学理论对大学生素质进行科学评价[J].河北科技大学学报(Journal of Hebei University of Science and Technology),1999,20(2):29-32.
[16]陈军霞,刘小玮,杨会琴.模糊数学在人才综合素质评价中的应用[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2001,22(1):80-83.
Evaluation method of students comp rehensive attributes based on connection numbera+bitheory
WANGWan-jun1,2
(1.Electronic and Info rmation Engineering College,Gansu Lianhe University,Lanzhou Gansu 730000,China;2.Info rmation Engineering College,Lanzhou University,Lanzhou Gansu 730030,China)
There are many subjective and indefinite facto rs in evaluation of students comp rehensive attributes.This paper p roposes a new evaluation method based on connection numbera+bitheory and builds a app rop riate evaluation model.This method avoids the disadvantagesof other evaluation methods and guarantees the objectivity and justnessof the results.Finally an examp le p roves the feasibility and efficiency of the p roposed method.
a+bitheory;connection number;students comp rehensive attributes;evaluation method
O159
A
1008-1542(2010)06-0508-04
2010-06-30;责任编辑:陈书欣
王万军(1974-),男,甘肃天水人,讲师,硕士研究生,主要从事粗集理论、联系数理论、数据挖掘、知识发现等方面的研究。

