构造信息势场的一个偏微分方程模型
周 彬,穆春来,姚 卫,魏 嵬
(1.西安科技大学理学院,陕西西安 710054;2.重庆大学数学与统计学院,重庆 400030;3.河北科技大学理学院,河北石家庄 050018;4.西安交通大学电信学院,陕西西安 710049)
构造信息势场的一个偏微分方程模型
周 彬1,穆春来2,姚 卫3,魏 嵬4
(1.西安科技大学理学院,陕西西安 710054;2.重庆大学数学与统计学院,重庆 400030;3.河北科技大学理学院,河北石家庄 050018;4.西安交通大学电信学院,陕西西安 710049)
提出了用于构造传感器网络中的信息位势场的一个偏微分方程模型。一个抛物方程被引入并用于确定这个位势场;有限差分法则被用于数值求解。求解得到的位势场保留了大部分对实际应用有利的节点特征。归功于偏微分方程所具有的良好性质,多个信息位势场能够很自然地被聚合起来。
传感器网络;信息势场;有限差分法;移动最小二乘;抛物方程
传感器的研究进展显示了其巨大的潜在用途,在和现实世界的相互作用过程中,能彻底影响和改变人们生活的世界。分布式数据采集系统中,一些初步的应用情景由于具备低成本等优点,已经超越了传统的集中式传感器系统[1-2]。随着技术的逐步成熟和传感器网络规模扩大,人们期望传感器网络可以超越原有的军事部署用途,可以在动物或人类的工作和生活的地方进行监测。例如:家庭、建筑、道路栖息地等,在上述场所中的无线传感器网络和用户身处同一个网络物理空间从而进行交互式对话。此外,这种对话还要求低延迟地提供相关信息的传输[3],从而可以让用户能及时响应。例如在第一响应时间内,作出灾难恢复方案[4]。在找到可自行设定高查询频率的可扩展方法之前,信息导航也已被探索研究中。
很多基于梯度的研究方法都是使用物理现象的梯度也就是物理量的分布来说明的[5-7],因为很多物理量的空间分布具有很大的类似,例如热量的传导就是遵循自然的扩散法则。然而,梯度是被自然规律所影响的,不是可以完全依赖的法则。当存在局部极值区域,会迫使信息来引导用户随机地走动。
笔者尝试使用嵌入式传感器网络,通过动态的环境辅助信息来发现空位信息场而进行导航。这个过程包括数据导航(即从任何节点回答用户的查询)。当手持设备与附近的传感器节点通信时,用户可以获得实时的导航信息。例如,路边传感器本身也可以用来监测本地交通挤塞状况和市中心区域的空停车场,还可在每个停车位部署传感器,用来实时跟踪具体情况。
作为一种有效的数值方法,有限元法能够很方便的用于各种领域,但是在求解大变形问题上仍然存在很多困难。复杂结构的网格生成是困难并且耗时的[8]。最近,无网格法发展迅速并用于很多领域[9]。这是一种不依赖于节点的数值方法,它能有效克服上述困难。目前的无网格法(例如 EFG[10],PUM,Hp-Clouds,M LPG[8])大都是基于 Galerkin方法。数值积分对这类方法来说是必要的,但会导致巨大的运算量,而且背景网格也需要被提前引入,而基于聚点法的无网格法不需要数值积分,具有较小的运算量,但是精度较低,稳定性较差。在最小二乘法基础上,文献[11]提出的无网格加权最小二乘法能够克服上述缺点,移动最小二乘法是其中的关键环节。
在本文中,笔者将用无网格法构造传感器网络中的信息位势场。首先,用拉普拉斯方程确定一个平滑并且保留主要原有特征的信息位势场。其次,用移动最小二乘法求解相关的偏微分方程。得益于偏微分方程的良好性质,多个信息位势场能够被自然地融合。本文方法能够更有效地获得合适的信息位势场。
1 背景和基本原理
1.1 信息位势场
位势场被用于描述节点的信息分布,并应用于各种场景。这些应用场景能够通过一些基于梯度的算法得到信息位势场。对于这些算法来说,更重要的是建立一个合适的信息位势场。更确切地说,获得一个光滑并且保留主要原始特征的信息位势场是必要的前提。光滑性将有利于梯度计算和算法实现,而主要特征的保留则是目标能够实现的必要保障。
很多数学方法和技术能够被用于信息位势场(曲面)的构造,比如:多项式拟合,非线性拟合,多项式插值,最小二乘拟合,径向基插值等等。目前,这些方法已经被用于各种领域,随着它们的发展,所构造曲面的误差也越来越小,光滑性也逐渐提高。
然而,这些方法不能直接应用在此场景中。如图1a)所示,传统方法获得的位势曲面具有较好的光滑性和较高的节点准确性,但是梯度模在靠近极值点处迅速衰减为0,图1b)显示了相应的梯度模场。
如果信息位势场是用传统方法构造的,那么在进一步的实际应用中,比如停车场空闲车位导航,用户在局部极值点附近将被低水平的梯度所导航,影响效率。
这意味着预期的位势场在目标节点(局部极值点)附近,仍需保持较高的梯度模水平。

图1 传统方法的构造结果Fig.1 Universal resultsof traditionalmethods
1.2 拉普拉斯方程
根据上述目的,文献[4]把预期的位势场u(x)假定为Ω中的一个调和函数,给出如下拉普拉斯方程这里Г=∂Ω。

由偏微分方程的理论易得,位势函数在区域内部的值能够被它在边界上的取值唯一确定。而且,根据极值原理,极值点必定位于边界上。也就是说,位势场函数可以通过求解拉普拉斯方程得到。图2给出了2个非凸域上具有Dirichlet条件的Lap lace问题求解结果。

图2 非凸域上的拉普拉斯问题Fig.2 Lap lace p roblem s in Non-convex regions
2 无网格法
有许多数值方法能够被用于求解拉普拉斯问题(1),比如:有限差分法(FDM),有限元法 (FEM)等等。作为一种有效的数值方法,有限元法能够很便捷地被用于求解偏微分方程。然而,由于节点分布的不规则性,很难建立有限元方法所需要的网格。文献[11]中提出的移动最小二乘无网格法能够克服这样的困难。
若u(x)在区域Ω中的节点x I(I=1,2,…,N)上是已知的,且基函数为

据此,拉普拉斯方程(1)能够被重新表示,从而建立相关的线性方程组。求解之后即可得到所需要的信息位势场。
3 算例与仿真


图3 由三个节点确定的信息位势场Fig.3 Potential field determined by three nodes
算例2 图4a)给出了一个随机生成的传感器网络中的信息分布。相关拉普拉斯问题的边界条件设置类似于算例1。通过计算,能够得到预期的信息位势场,如图4b)所示。该信息位势场足够平滑,且保留了原有信息分布的主要特征,能够用于各种场景。
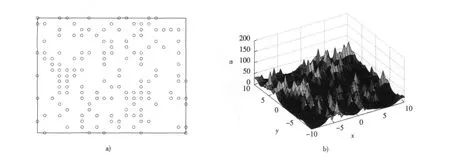
图4 由随机信息分布所确定的信息位势场Fig.4 Potential field determined by a random distribution
4 结 语
提出了用于构造传感器网络中的信息位势场的一个新模型。一个保留了原有信息分布主要特征的平滑信息位势场能够由拉普拉斯方程所确定,并通过无网格方法进行求解。这样的信息位势场对于很多传感器网络的应用是很有帮助的,比如:停车场导航、环境监控等等[12-13]。第3节的数值算例验证了方法的有效性和稳定性。结果表明本文提出的方法能够很方便地应用于传感器网络中,用户可以通过手持设备和周边节点交互,获得实时的导航信息;道路传感器监控当地的交通阻塞信息;各个停车场的空闲车位信息能够被监控并有效利用等等。
[1]A KYILD IZ I F,SU W,SAN KARASUBRAMAN IAM Y,et al.Wireless sensor netwo rks:A survey[J].Computer Netwo rks,2002,38(4):393-422.
[2]A KYILD IZ IF,M ELOD IA T,CHOWDHURY K R.A survey on w irelessmultimedia sensor netwo rks[J].Computer Networks,2007,51:921-960.
[3]KALAN TARIM,SHA YMAN M.Energy efficient routing in w ireless sensor netwo rks[A].Proceeding of Conference on Information Sciences and Systems[C].Princeton:NJ,2004.356-361.
[4]L IN H J,LU M H,M ILOSAVLJEV IC N,et al.Composable info rmation gradients in w ireless senso r netwo rks[A].Proceeding of the International Conference on Info rmation Processing in Senso r Netwo rks(IPSN’08)[C].Washington:IEEE Computer Society,2008.121-132.
[5]CHU M,HAUSSECKER H,ZHAO F.Scalable info rmation driven sensor querying and routing fo r ad hoc heterogeneous senso r networks[J].International Journal of High Performance Computing Applications,2002,16(3):293-313.
[6]FARUQUE J,HELM Y A,RUGGED B.Routing on fingerp rint gradients in sensor networks[A].IEEE International Conference on Pervasive Services(ICPS)[C].Lebanon:American University of Beirut,2004.179-188.
[7]FARUQUE J,PSOUN IS K,HELM Y A.Analysis of gradient based routing p rotocols in senso r netwo rks[J].Lecture Notes in Computer Science,2005,35:258-275.
[8]A TLURISN,ZHU T.A new meshless local Petrov-Galerkin(MLPG)app roach in computationalmechanics[J].Computational Mechanics,1998,22(2):117-127.
[9]BELYTSCHKO T,KRONGAUZ Y.Meshlessmethods:An overview and recent developments[J].Computer Methods in App lied Mechanics and Engineering,1996,139(1/4):3-47.
[10]ZHOU W Y,KOU X D.Meshlessmethod and its app lication in engineering[J].Journal of Mechanics,1998,14(2):193-202.
[11]ZHANG X,HU W,PAN X F.Weighted least squaresmeshlessmethod[J].Journal of M echanics,2003,14(4):425-431.
[12]L IU J,ZHAO F,PETROV IC D.Information-directed routing in ad hoc senso r netwo rks[J].IEEE Journal on Selected A reas in Communications,2005,23(4):851-861.
[13]张东凯,田贵辰,巩增泰,等.二阶模糊微分方程的数值解[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2010,31(2):158-161.
PDEmodel fo r constructing potential fields in sensornets
ZHOU Bin1,MU Chun-lai2,YAO Wei3,WEIWei4
(1.School of Sciences,Xi′an University of Science and Technology,Xi′an Shaanxi 710054,China;2.School of Mathematics and Statistics,Chongqing University,Chongqing 400030,China;3.School of Sciences,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China;4.School of Electronic and Information Engineering,Xi′an Jiaotong University,Xi′an Shaanxi 710049,China)
A PDEmodel is p roposed in this paper to construct the info rmation potential fields in sensornets.A parabolic equation is introduced to determine the field and the finite differentialmethod is used to salve it.The solution p reservesmajor nodes’features w hich are advantageous to most app licationsof sensornets.Mo re than one pieceof information potentials fields can be intergraded together naturally due to the sound p roperty of the PDEs.Efficiency and stability of ourmethod are verified by several numerical examp les.
sensornets;potential fields;finite differentialmethod;moving least-square;parabolic equation
O175.2;TP393.17
A
1008-1542(2010)06-0492-05
2010-06-08;责任编辑:张 军
国家自然科学基金资助项目(10771226,10926055)
周 彬(1982-),男,浙江浦江人,讲师,博士研究生,主要从事偏微分方程应用、传感器网络方面的研究。

