一种求解有限域 Fq上线性方程组的有效算法
周晓谊,马纪新,杜文才,陈明锐
(1.海南大学信息科学技术学院,海南海口 570228;2.格林威治大学计算与数学学院,英国伦敦 SE10 9LS)
一种求解有限域 Fq上线性方程组的有效算法
周晓谊1,2,马纪新2,杜文才1,陈明锐1
(1.海南大学信息科学技术学院,海南海口 570228;2.格林威治大学计算与数学学院,英国伦敦 SE10 9LS)
在对重线性化方法的研究中提出的一种对有限域 Fq上线性方程组的算法,利用有限域xq-1=1的性质,可以快速地对方程组进行高斯消元,从而求出方程通解.
有限域;线性方程组;高斯消元
有限域的起源可以追溯到 17和 18世纪,许多大数学家如费尔马 (P de Fermat)、勒让德 (A M Legendre)、欧拉 (L Euler)和高斯 (C F Gauss),他们在研究数论的一些性质时,得到了许多同余式的性质.这实质上也研究了有限域的许多性质,但是他们还没认识到“域”的概念.直到 19世纪韦伯 (H Weber)对伽罗华(E Galois)的工作给予抽象描述,才有了域的定义.韦伯提出域是群的推广形式,并且运用当时最一般的术语介绍了伽罗华理论,阐述了伽罗华理论不仅研究了方程的可解性问题,还研究了特殊的群与某种良好定义的域的相互作用问题.1930—1931年,威尔登 (B L Van derWaerden)出版了《近世代数学》一书,是代数学成为研究抽象代数结构的一门结构数学.至此,有限域的理论基本成熟.
有限域具有许多优美的特性,在组合设计、编码理论、信息安全、代数几何学、数论、群论、离散数学和通信系统等许多实际领域有着广泛的应用.特别是最近几十年,随着计算机技术的蓬勃发展,有限域的地位愈加重要,例如有限域的计算和算法分析对计算机代数和符号计算的影响,有限域上的离散对数问题.在密码算法和安全协议的设计等方面有着广泛的应用,以及近几年来密码学的研究热点——基于 MQ(Multivariate Quadratic,多元二次多项式)问题的公钥密码等.
实际上,许多工程计算问题和理论问题最终都可以归结为线性方程组的求解问题,如反演问题、优化问题、数据拟合问题、插值问题、纠错码设计、多元多次方程组的求解问题[1]等.鉴于线性方程组在实际中的重要应用,多年来在探求其求解的研究上也取得了许多有价值的成果,目前求线性方程组的方法主要有直接法和迭代法.某些多元二次方程组的求解也是基于这 2种方法,如重线性化 (Relinearization)方法.该方法于 1999年由 Kipnis和 Shamir首先提出[2],其基本思想是通过对方程数量小于变元数量之方程组的通解表示,构造出更高次的方程,从而使最终得到的高次方程的总数大于或等于新变元的数量,其次得到的高次方程中的新变元,也将视为互不联系的一次变元,即线性方程组所看待,最后通过解该高次方程组反推出原方程组的解.
笔者在用重线性化对有限域上多元二次方程组进行密码学分析时,发现利用有限域xq-1=1的性质,可以快速地对方程组进行高斯消元,从而求出方程通解.相比于整数域上的线性方程组所使用的高斯消元方法来说,该方法更加简单易行.
1 算法设计
有限域上线性方程组的定义
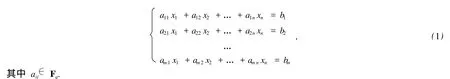
令方程组增广矩阵的秩为R(A),则关于方程组(1)的基础解系有以下结论:
1)R(A)>n时,方程组(1)没有解;
2)R(A)=n时,方程组(1)仅有零解,无基础解系;
3)R(A)=r 方程组(1)的通解可表示为 求解思路: 1)用行初等变换,将方程组 (1)的增广矩阵化为广义上三角形矩阵,且对角线元素均为 1; 2)新增行向量,将第 1)步得到的矩阵化为单位拓展矩阵; 3)将新增行向量中带 1的元素设为方程组的自由未知量,如xr+1,…,xn(r=R(A)); 4)从第R(A)行开始,一步步往上迭代,最终求得方程组的通解. 定义 1[3]设(F,+,×)是一个代数系统,+和 ×都是二元运算.F至少有 2个元素;+满足结合律、交换律,存在单位元 0,且对任意aF,存在逆元素 -a;×满足结合律、交换律,存在单位元素 1,且对任意a≠0,aF,均有逆元素a-1,并且 ×对 +满足分配律,则称(F,+,×)为域. 从以上定义可知,对于有限域F,每个元素a都存在a-1使得a×a-1=1. 因此,对于有限域上线性方程组的系数aij,总存在另一个元素bij=使得aijbij=1.利用这一性质可以对线性方程中的任意系数进行求逆设置,使其为 1. 另 Ab为线性方程组 (1)的增广矩阵.求解思路如流程图 1所示. 定义 3[4-5]设Am×n(m 求通解算法如下 定义 2[3]只含有限个元素的域称为有限域. 方程的解只由 Z表示,因此从最后一行开始,依次求得各未知数的值,将其存放到 Z:for i=1to r 将原方程 r-i+1行等式右边的值存放到 Z(r-i+1,M+1)中,即 Z(r-i+1,M+1)=Ab(r-i+1,C) 图1 有限域 Fq上高斯消元的流程图 时间复杂度:该算法主要由高斯消元和求通解 2个部分构成. 在高斯消元中,由图 1可知该过程有 2个循环语句,在最坏情况下,即对角线元素为 0,此时该程序所运行到的行需要和其下面的行进行比较交换,直到对角线元素不为 0或者比较到最后一行为止.假设每种情况的出现概率为p,则改算法平均时间复杂度为与输入方程组的方程个数m,以及方程的秩有关.即复杂度为 最差时间复杂度:O(R(A)3). 最优时间复杂度:O(R(A)),即对角线元素都不为 0,不用与其他行进行比较. 平均时间复杂度:O(R(A)3/m). 求通解的过程由 3条循环语句构成,与方程的秩R(A)和未知数的个数n有关,因此时间复杂度为R(A)×(n-R(A))×n(n-1)(n-2)/6. 空间复杂度:算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小,它包括为参数表中形参变量分配的存储空间和为在函数体中定义的局部变量分配的存储空间 2个部分[6].因此该算法的空间复杂度主要由方程组的未知数个数n、方程系数矩阵的秩R(A)以及方程个数m有关,因此有 从方法的计算原理、过程和算例结果来看,本文提出的算法对于计算有限域上的线性方程组具有算法简单、编程容易的特点.计算结果表明,此方法适用于任何线性方程组.但是算法的时间空间复杂度分析表明,在高斯消元过程中,判定对角线元素是否为 0并且进行行交换时耗费了较多时间,该方法可通过增设一个一维数组来记录某行元素特点适合交换到第几行,一旦交换后数组中与行数相对应的元素设为1,则表明该行之后不用再交换.本文算法作为一种求解有限域上线性方程组的方法,具有一定的理论意义和实用价值. [1]徐勤花,史文谱,陈瑞平,等.求解线性方程组的超几何球法[J].烟台大学学报:自然科学与工程版,2007,20(2):92-94. [2]KIPN ISA,SHAM IR A.Cryptanalysis of the HFE Public Key Cryptosystem byLinearization:ProceedingsAdvances in Cryptogoly-CRYPTO′99,19th Annual International Cryptology Conference,Santa Barbara,August 15-19,1999[C].London:Springer-Verlag,1999. [3]朱平天,李伯葓,邹园.近世代数[M].北京:科学出版社,2003. [4]王文贤.线性代数及其应用[M].大连:大连理工大学出版社,1993. [5]陈建莉.线性方程组解法新探[J].纺织高校基础科学学报,2008,21(2):238-241. [6]严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,2000. An Efficient Algorithm to Solve L inear Equations over F inite Field Fq ZHOU Xiao-yi1,2,MA Ji-xin2,DU Wen-cai1,CHEN Ming-rui1 (1.College of Information Science and Technology,Hainan University,Haikou 570228,China;2.School of Computing andMathematical Science,University of Greenwich,London,UK,SE10 9LS) In our report,an effective algorithm for linear equations over finite field Fqwas proposed,and with the property ofxq-1=1 over finite fields,the algorithm could conduct Gaussian elimination and obtain common solution. finite field;linear equation;Gaussian elimination O 241.6 < class="emphasis_bold">文献标志码:A A 1004-1729(2010)04-0306-05 2010-06-12 海南省高等学校科学研究项目 (Hjkj2010-10) 周晓谊 (1979-),女,海南海口人,海南大学信息科学技术学院讲师. 陈明锐 (1960-),男,海南大学信息科学技术学院教授.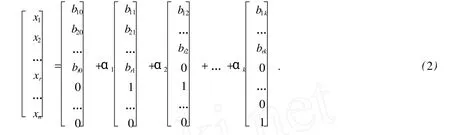
1.1 高斯消元
1.2 求通解


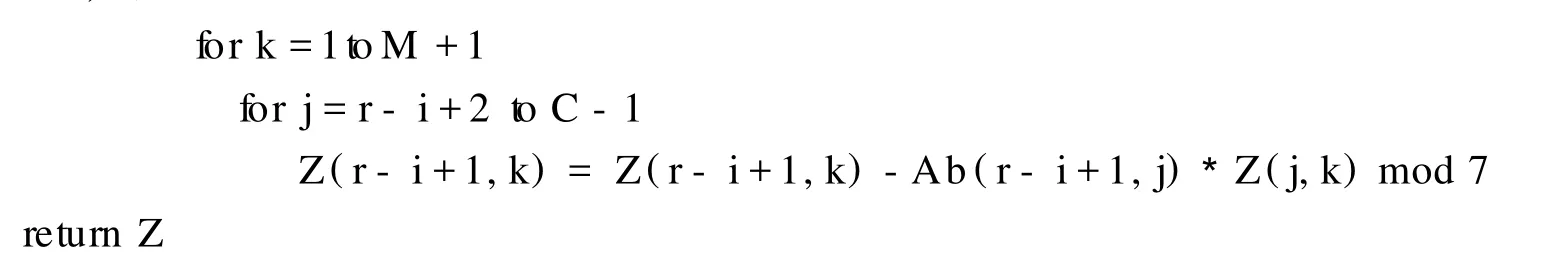
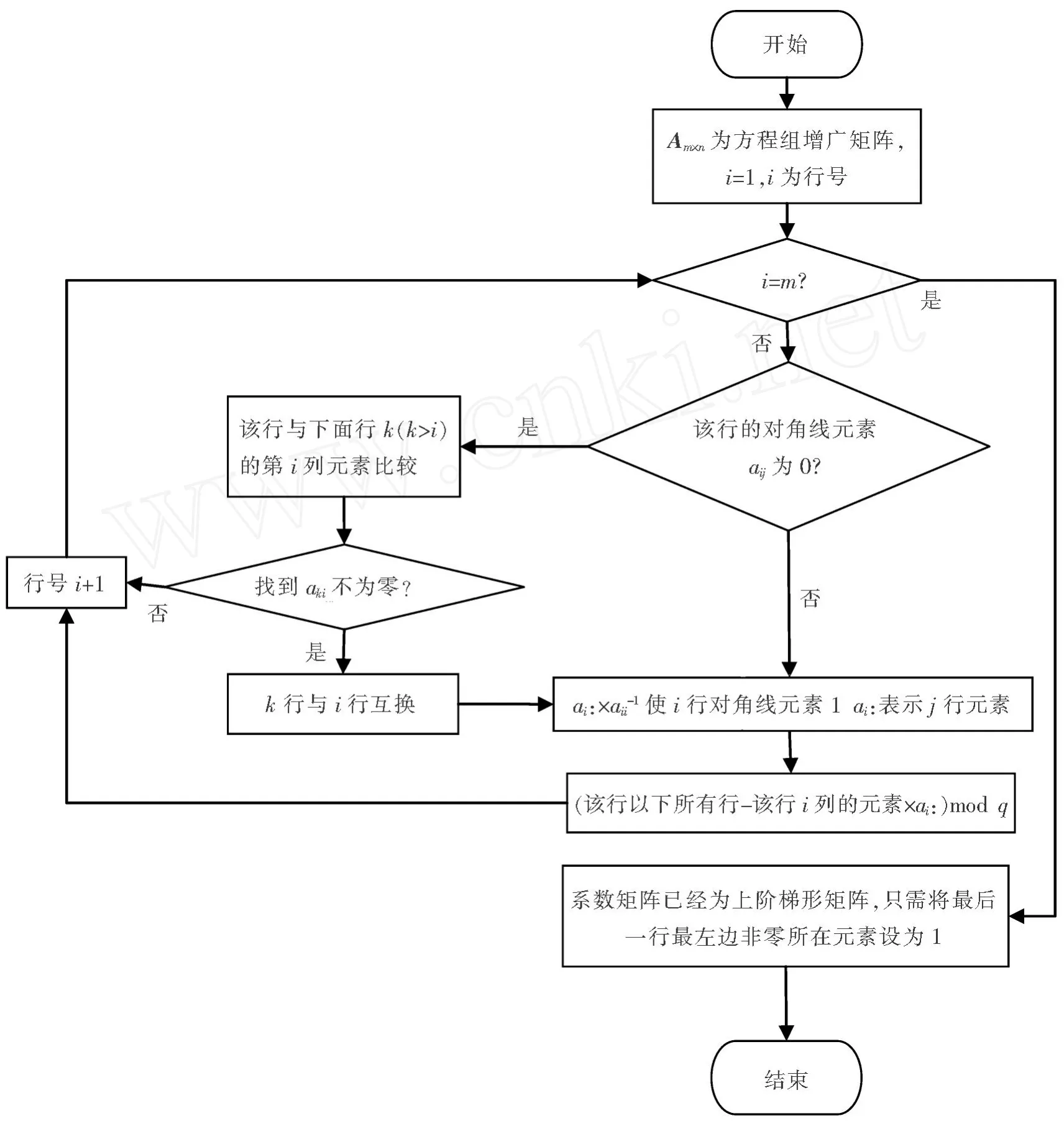
1.3 算法复杂度分析
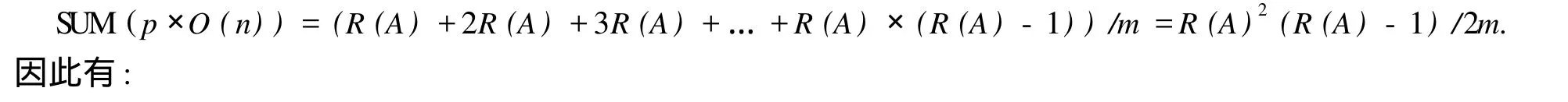
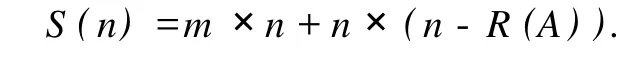
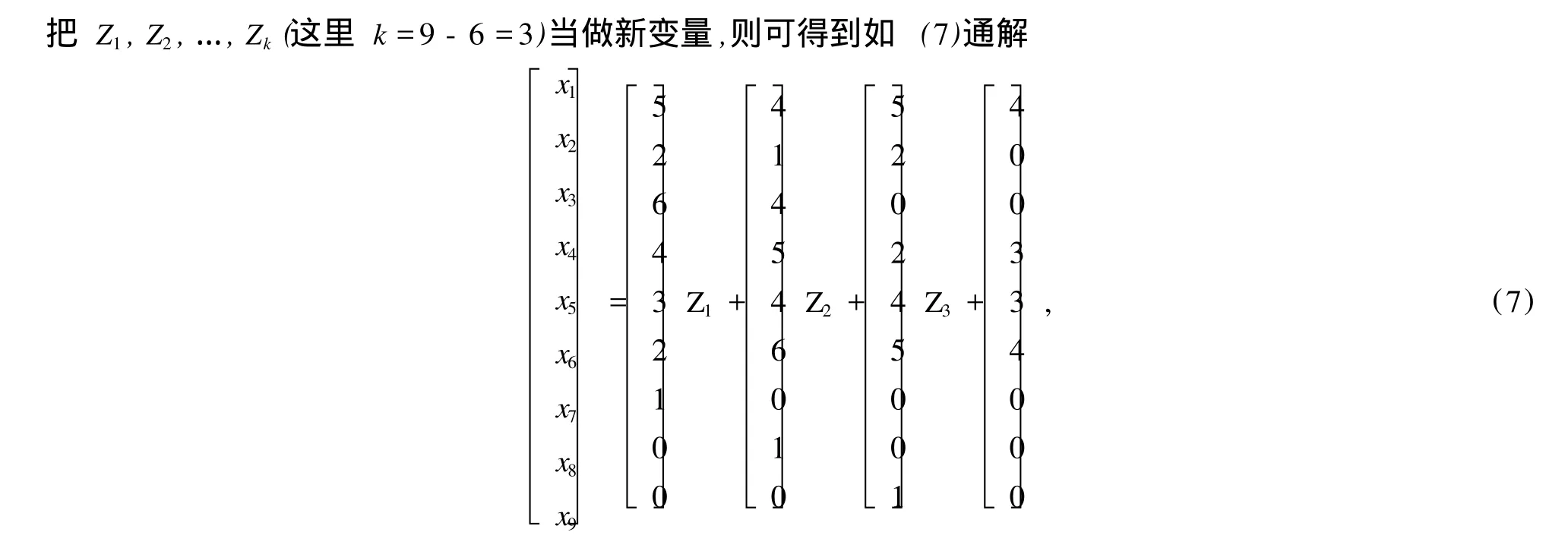
2 应用实例

3 小 结

