矿井围岩与支护系统复杂性研究

孙广义

(黑龙江科技学院 资源与环境学院,哈尔滨 150027)

矿井围岩与支护系统复杂性研究

孙广义

(黑龙江科技学院 资源与环境学院,哈尔滨 150027)

为研究围岩与支护技术问题,对近十年来相关研究工作进行了系统分析,发现围岩与支护是相互作用、相互制约的一个复杂非线性系统。利用力学与非线性系统理论建立了围岩与支护系统的耗散结构模型,论述了围岩熵产生与支护熵流的相互关系。根据信息熵的原理建立了矿井支护可靠熵模型,并与结构可靠性进行对比分析。最后提出深部巷道断面优化设计,降低巷道底角的非线性应力集中状态,实际应用中使巷道底鼓量减少 20%以上。

围岩与支护;耗散结构;可靠熵;非线性

0 引 言

矿井支护是安全高效的前提,其成本占回采与掘进的 30%左右。由于矿井生产条件的随机性和模糊性,以及人们对一些支护技术和理论认识的未确定性[1-2],一些支护问题没有彻底的解决。目前的支护理论与方法,因理论、方法与角度的不同,其结果也不同。在应用过程中,按不同的理论方法得出不同的结果[3-4];即使采用同一种理论模型,不同的工程技术人员由于自身经验和技术水平的差异,也可能得出不同的结果[5]。这给支护设计可靠性带来一定的影响。

随着矿井开采深度的增加,浅部开采支护的一些理论已不适应深部开采的需求[6]。深部开采受高应力等因素的影响,围岩表面形成裂隙、扩容等现象,属于不连续变形,使岩石力学曲线峰后一段的距离,出现非线性大变形[7]。受研究的方法、手段与设备等限制,深部巷道支护研究的一些问题仍不清楚[8],很多问题是半知识、半经验的问题[9]。因围岩受节理裂隙的影响,故难以建立符合井下实际生产条件的力学非线性模型[10]。即使建立了力学非线性模型,因非线性力学模型的高度复杂性,很难得出解析解,仅能利用数字模拟方法求解[11-12]。

综上所述,笔者把矿井围岩与支护看作是一个复杂的系统,采用力学与复杂系统理论进行研究,力求解决矿井复杂的非线性围岩与支护的技术问题。

1 矿井支护系统的耗散结构

1.1 矿井支护是一个复杂开放系统

如果将矿井围岩与支护看作是一个开放的复杂系统[13-14],那么,主要表现在以下几个方面:一是系统之间存在信息和能量的交换[15]。围岩从支架中吸取能量,保持其自身的稳定性;反过来围岩又给支架一定的压力,使其变形和收缩,支架又从围岩中吸收能量。围岩与支架是一个相互制约、相互依赖和相互作用的系统。二是围岩与支护系统可划分为很多子系统,如围岩系统、应力场系统、支架系统等。三是系统的宏观稳定性、微观系统可分别通过井下观测、实验来研究,但是人们对中间的一些层次结构耦合作用关系认识的还不完全清楚[16]。

“耗散结构”理论认为[17],对于一个与外界有物质或能量交换的开放系统,其系统熵的变化可以划分为两个部分:一部分为系统内部由于不可逆过程所引起的熵增原理,称为熵产生,用diS表示,且diS≥0;另一部分是系统与外界进行物质和能量交换引起的熵,称为熵流,用deS表示。整个系统的熵随时间的变化率dS可以看作是熵产生和熵流随时间变化率之和:

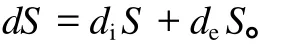
deS为负值,表示系统外界的熵流向系统内部提供输入能量,使整个系统向有序的方向发展,减少熵产生和系统的无序程度;deS为正值时,系统外界的熵流向系统内部提供输出能量,加快系统向无序的方向发展。

1.2 矿井围岩与支护系统的耗散结构分析

巷道开掘后,围岩在其地应力的作用下会发生变形、甚至冒落等矿山压力显现现象。根据耗散结构原理,围岩在地应力作用下的变形显现的过程是熵产生现象。熵产生是矿井围岩固有的一种不可逆现象,且围岩总是存在压力或变形,即熵产生为正数[15]。支护系统给围岩提供的支护能量是产生熵流的现象,这时围岩从支护体中吸收熵流,使围岩与支架系统有压力或能量的交换,即围岩与支护系统的熵交换[18]。

巷道围岩产生强烈的变形或冒落等现象,是熵产生增大原理。这种现象是围岩与支护系统远离平衡状态,为熵增加现象。在熵流一定的前提下,熵产生越大,围岩变形量也越大,支护系统熵也越大,矿井支护系统趋向失稳。矿井支护的目的就是降低围岩变形量、向围岩内部提供负熵流,使围岩与支护系统的总熵值减少[19]。当围岩与支护系统到达某种平衡或近似平衡状态时,熵产生与熵流处于平衡状态,围岩变形基本处于稳定的状态。

1.2.1 熵函数

Se为巷道与围岩系统的支护熵流,是支架支撑能力、围岩层间胶结能力和围岩变形边缘产生的拉应力的总和[20],如图 1所示。Si为围岩与支护系统中围岩变形引起的熵产生。局部熵平衡方程为:

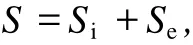
式中:S——围岩与支护系统的总熵。

图1 围岩与支护系统的熵Fig.1 Surrounding rock and support system’s entropy

系统总熵随时间的变化率为:

式中:V——围岩影响范围内的体积;

A——支护体对围岩产生的有效支撑范围;

pA——围岩对支护体产生的压力;

ρ——单位面积支护密度;

ε——支护体的刚度系数;

k1——顶板岩层胶结力系数;

k2——围岩压力引起的熵产生;

k3——围岩变形引起的熵产生。

式(1)中支护体的熵流随时间的变化率为

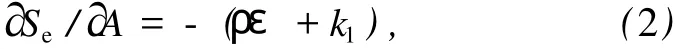
而由围岩压力与变形引起的熵产生的变化率为

1.2.2 熵函数分析

从式(3)可以看出,熵产生包括由顶板压力引起的熵产生和围岩变形扩容等引起的熵产生两部分。支护熵流越大,围岩变形量越小;而支护系统的总熵越小,支护系统可靠性越大。因支护系统提供的熵流绝对值不可能大于熵产生,故最佳状态是熵流等于熵产生,支护系统的总熵为零,围岩与支护系统处于低熵状态。

巷道支护初期,一般也是矿山压力显现的活跃时期。这时,支护与围岩系统是处于耗散结构的非线性远离平衡状态。围岩压力微小变化都会引起支护系统的变化,这种涨落现象是远离非平衡的线性区[21]。支护系统不稳定,使围岩向稳定或变形加大的方向发展。

当围岩与支护系统处于线性平衡状态条件时,围岩基本处于稳定状态。根据式(2)、(3),有

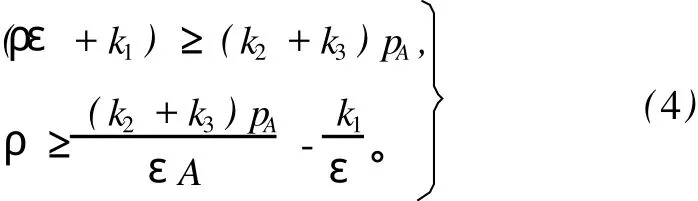
式(4)说明支护密度ρ不仅与围岩变形量及支护的支撑能力有关,还与围岩变形及胶结能力有关[20,22]。如果不考虑k3和k1因素的影响,即k3=k1=0,则

式中:k2pA——顶板压力;

εA——支撑能力。

这时,式(5)变为普通常规的顶板压力与支护密度选择的计算模型。

1.3 围岩与支护系统稳定性

1.3.1 线性平衡稳定性

把熵产生k2、k3看作是顶板压力与围岩变形量的函数。在近线性平衡区,顶板压力可简化为围岩变形的线性函数。其变化率为:

满足式(6)条件称为耗散结构的平衡线性区,支架与围岩基本处于稳定状态。

1.3.2 非线性平衡稳定性

在非线性平衡区内支护系统的稳定性由超熵来判别。为保证超熵大于等于零,使围岩支架系统向稳定状态方向发展,支护系统必须满足:

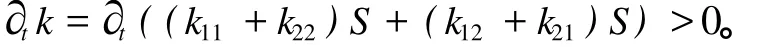
k11、k22是唯象系数,表示顶板压力与围岩变形量关系(强弱)的系数,是围岩条件、支架适应性和顶板压力之间相互作用系数。保证k12、k21随时间的变化率为正数,随着时间的推移,才能保证支护系统由不稳定状态向稳定状态方向发展。

2 矿井支护系统复杂可靠熵

2.1 信息熵原理

信息理论中的“信息量”被定义为[23]

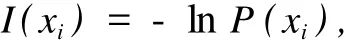
式中:P(xi)——xi的概率。

而信息熵是表示平均信息量不确定程度的度量,为信息量的数学期望值E(I(xi))。那么,信息熵H(x)定义为:

离散随机变量信息熵

连续随机变量的信息熵

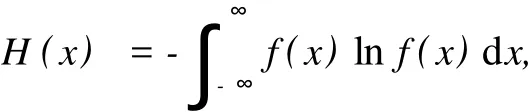
式中:f(x)——连续随机变量分布密度函数。

非标准正态分布函数的信息熵H2(x)

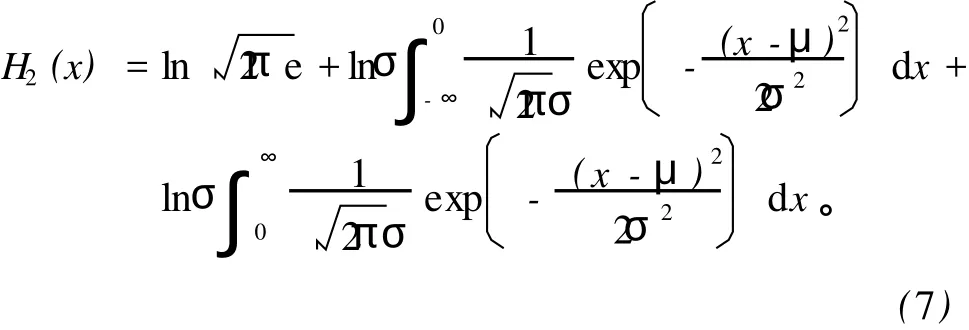
而最大信息熵为

信息熵表示实验之前平均信息源不确定[24-25]的度量,或实验后信息量多少的度量。熵值越大,表示系统的不确定程度越大[26]。随机变量的方差越大,其信息熵值也越大,说明系统越混乱。

2.2 矿井支护系统可靠度熵函数[27]

结构可靠性概率表达式为[28]

某工程的可靠性表示完成其预定功能的概率[29-30],是设计阶段的可靠性,而信息熵是表示系统不确定性的度量,兼顾了对施工的影响。把可靠性[31-32]与信息熵联合起来,既表示工程设计时的平均可靠性,又表示施工过程中实现可靠性的难易程度,是一个综合反映可靠性的指标。所以,工程结构可靠度指标(9)与信息熵(方差对数)的乘积称为可靠度熵函数,

可靠度熵函数为一个单值函数,计算方便,便于推广应用。

2.3 矿井支护系统可靠熵

矿井支护系统可靠熵为

式(10)中H2(x)为矿井支护系统实际发生的熵,且熵越小,系统的有序程度或可靠性越高; Hm(x)为矿井支护系统的最大熵,是矿井支护工程系统中某一范围的总熵。所以,H2(x)/Hm(x)越小,支护系统的可靠熵越大。

可靠性、可靠度指标、可靠熵与可靠度熵函数等指标的比较结果见表 1(以正态分布函数为例)。

表 1显示,可靠度熵函数与可靠度指标变化规律基本一致,但是可靠度指标在小失效概率范围内变化大,稳定性差,而可靠度熵函数变化相对较小,稳定性好[33]。

表 1 可靠性、可靠度指标、可靠熵与可靠度熵指标比较Table 1 Comparison of rel iability,rel iability index,rel iable entropy and rel iability entropy index

3 深井巷道围岩非线性变形

在深井高地应力作用下,巷道围岩变形及扩容等现象,表现出不连续的非线性大变形特征[34-35]。

3.1 深部巷道围岩非线性变形的主要特征[36-37]

深部巷道非线性变形是在围岩的表面破裂范围内,即不连续非线性变形范围。虽然破裂的围岩还能承担一定的力学特征,如果不能及时有效控制围岩非线性变形的范围,变形破裂的范围就逐步扩大,最终导致巷道失稳破坏。巷道围岩变形范围R的非线性模型为:

式中:r0——巷道半径;

γ0——岩层容重;

H——采深;

C0——内聚力;

φ——内摩擦角;

p——巷道支护强度。

巷道底板一般不支护,特别是巷道底角应力集中程度高,使巷道底板产生非线性的变形与破坏。

3.2 降低巷道底角非线性应力集中区域[38-39]

我国煤矿井下巷道一般为矩形、梯形、直墙拱形(如三心拱形、半圆拱形、圆弧拱形)等直角为底角的断面形状。以直角为底角的巷道应力集中系数最大处在巷道两个底角,是非线性应力集中区域,承载能力最弱处是巷道底板。在非线性高应力状态下,巷道底角处首先破坏,引起围岩变形量加大。

通过非线性有限元优化研究,采用将直墙拱与全封闭拱相结合的一种半封闭断面形态。此断面形态为拱形顶板、直墙、弧形底角、平底,如图 2所示。这种巷道断面最为重要的功能是改善巷道围岩的非线性应力分布,提高自身承载能力,减小巷道围岩的破坏范围。

图2 弧形底角巷道断面Fig.2 Section design in arc of base angle tunnel

经非线性有限元分析,将弧形底角与常规的直角底角巷道断面的应力、变形情况进行计算,部分结果如图3所示。

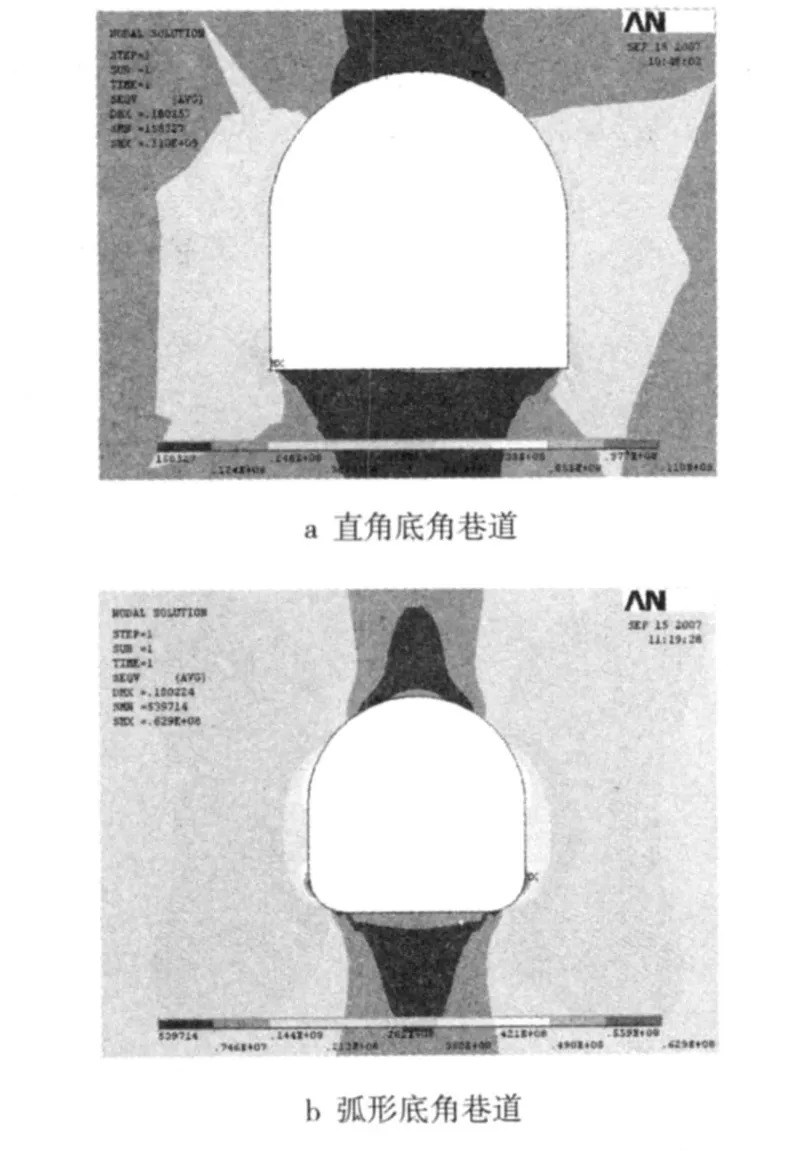
图3 有限元数字计算应力分布Fig.3 Stress distribution of fin ite element digital computing

3.3 应用实例

在开采深度为1 050m的某矿五采区四段进行了试验。回风下山及轨道下山分别采用了弧形底角、直角底角的巷道断面。两个巷道布置在同一个层位,间距 20m。巷道采用半圆拱型,宽 4.0 m,高 3.9 m,支护方式与参数相同,仅是巷道底角角度不同。观测期间弧形底角巷道顶底板最大移近量为 16 mm,直角底角巷道顶底板最大移近量为23mm,减少了30%。弧形底角巷道两帮最大移近量 14mm,直角底角巷道两帮最大移近量30mm,减少了53%。

4 结 论

(1)矿井围岩与支护存在随机性、模糊性与复杂性,特别是深部巷道围岩具有非线性大变形的特点。所以,矿井围岩与支护是一个复杂的系统,需要利用力学与非线性系统理论来研究,为矿井支护系统研究提供一个新方法。

(2)可靠度指标仅考虑均值与方差的比值,而没有考虑施工过程中对可靠性指标的影响。可靠度熵函数则从信息熵与可靠度指标综合角度,取多次实验的可靠性平均值,是一个系统的可靠性度量,符合矿井实际工程特点。

(3)直角巷道的底角非线性应力集中程度高,是引起巷道非线性变形的主要因素之一。巷道留设弧形底角后,能够明显降低底角的非线性应力状态,减少围岩的移近量,特别是降低了巷道底鼓量,对深部巷道的稳定起到重要的作用。

[1] 赵俊楼,张香玲,张立华,等.煤巷锚网索支护矿压显现规律数值模拟研究[J].河北工程大学学报:自然科学版,2009, (4):79-83.

[2] 刘开第,吴和琴,庞彦军,等.不确定性信息数学处理及应用[M].北京:科学出版社,1999.

[3] 康 健,侯运炳,孙广义,等.未确知期望在煤层围岩稳定性分析中的应用[J].辽宁工程技术大学学报,2008,(5):689-691.

[4] 孙广义,马云东,李 东.顶板压力计算的盲数辨识研究[J].辽宁工程技术大学学报,2003,(增刊):7-8.

[5] 孙广义,马云东.围岩分类的未确定数学研究[J].矿山压力与顶板管理,2003,(S3):68-69.

[6] 何满潮,谢和平,彭苏萍,等.深部开采力学研究[C]//中国软岩工程与深部灾害控制研究进展.北京:中国岩石力学与工程学会,2009.

[7] 康红普.深部煤巷锚杆支护技术的研究与实践[J].煤矿开采,2008,(1):1-5.

[8] 康红普.煤矿深部巷道锚杆支护理论与技术研究新进展[J].煤矿支护,2007,(2):1-8.

[9] 王怀新.深井主要巷道支护方式的研究与应用[J].煤矿安全,2003,(8):25-26.

[10] 谢和平,左建平.岩石断裂破坏的声发射机理初探[G]//谢和平,彭苏萍,何满潮.深部开采基础理论与工程实践.北京:科学出版社,2006.

[11] 耿养谋,马植胜,刘 庚.煤层巷道锚杆支护稳定性数值模拟研究[J].辽宁工程技术大学学报,2004,(1):44-46.

[12] 刘红岗,贺永年,徐金海,等.深井煤巷钻孔卸压技术的数值模拟与工业试验[J].煤炭学报,2007,(1):33-37.

[13] 孙广义.矿井支护系统可靠性理论研究[D].阜新:辽宁工程技术大学,2003.

[14] 孙广义,马云东.矿井巷道围岩与支护系统稳定性的耗散结构[J].黑龙江科技学院学报,2007,17(3):169-172.

[15] 蔡绍洪,彭仕政,赵行知.耗散结构与非平衡相变原理及应用[M].贵阳:贵州科技出版社,1998.

[16] 秦四清.初论岩体失稳过程中耗散结构的形成机制[J].岩石力学与工程学报,2000,(3):265-269.

[17] 曹鸿兴.系统周界的一般理论——界壳论[M].北京:气象出版社,1997.

[18] 王 琪.复杂行为的遍历性,熵及其应用[J].同济大学学报,2001,(3):326-329.

[19] 徐祖信,GUERC R.熵在水分配系统优化设计中的应用[J].同济大学学报,1997,(1):71-76.

[20] 孙广义,马云东.矿井支护系统可靠度熵函数研究[J].黑龙江科技学院学报,2003,13(4):38-40.

[21] 孙光辉.信息熵与不确定性[J].青岛大学学报:自然科学版,2000,(3):50-51.

[22] 孙广义,刘东江,刘永立.煤矿瓦斯爆炸安全参数的混沌研究[J].黑龙江科技学院学报,2001,(1):44-46.

[23] 陈丽英.略论熵与不确定度的关系[J].长春光学精密机械学院学报,1999,(1):62-64.

[24] 邱菀华.管理决策与应用熵学[M].北京:机械工业出版社, 2002.

[25] 李习彬.熵—信息理论与系统工程方法的有效分析[J].系统工程理论与实践,1994,(2):37-42.

[26] ZHAO N ING,WU HUAMU.On entropy conditions of high resolution schemes for scalar conservation laws[J].Journal of ComputationalMathematics,2001,(4):381-384.

[27] 孙广义,马云东,肖福坤.矿井支护系统可靠熵研究[J].岩石力学与工程学报,2005,(增刊):5 198-5 202

[28] 赵国潘,金伟良,贡金鑫.结构可靠度理论[M].北京:中国建筑工业出版社,2000.

[29] 古德生,邓 建,李夕兵.地下金属矿山无间柱连续采矿可靠性分析与设计[J].中国工程学报,2001,(1):51-57.

[30] 苏永华,方祖烈,高 谦.大型地下采空区稳定可靠性分析建模方法探讨[J].中国矿业,1998,(4):69-72.

[31] 孙广义,马云东.回采工作面支护设计可靠性的研究[J].辽宁工程技术大学学报,2002,(4):433-435.

[32] 孙广义,马云东.单体液压支柱工作面支护可靠性研究[J].煤炭工程,2002,(9):32-34.

[33] 孙广义,李 波.回采工作面支护可靠性分析[J].黑龙江科技学院学报,2006,16(2):82-84.

[34] 姜耀东,赵毅鑫,刘文岗,等.深部开采中巷道底鼓问题的研究[J].岩石力学与工程学报,2004,(14):2 396-2 401.

[35] 高明中.巷道压曲性底鼓的机理与控制[J].安徽理工大学学报:自然科学版,2008,(1):20-24.

[36] 李志强.复杂应力条件下深部软岩巷道矿压控制研究[D].重庆:重庆大学,2006.

[37] 鸡西矿业集团.深部巷道非线性大变形机理研究科研报告[R].哈尔滨:黑龙江科技学院,2008.

[38] 孙广义,林井祥.深部巷道支护技术研究与实践[J].煤炭开采,2010,(1):54-57.

[39] 孙广义,陈 刚,于蒲喜.深部开采巷道断面优化设计与应用研究[J].煤炭工程,2008,(9):57-60.

Research on complexity ofm ine surrounding rock and its support system

SUN Guangyi
(College of Resource&Environment Engineering,Heilongjiang Institute of Science&Technology,Harbin 150027,China)

A imed at surrounding rock and support technique,this paper offers a systematic overview of research work done in recent decade and suggests the discovery that the surrounding rock and the supports represent a complex nonlinear system subjected to the interaction and mutual constraints.The paper introduces the surrounding rock and the support system’s dissipation structure model developed by using mechanical and the nonlinear system theory,and discusses the mutual relationship between the surrounding rock entropy’s production and the support entropy flow.The paper features the mine support reliable entropymodel according to the info rmation entropy’s theory,and offers a contrastive analysis of the structure reliability.The paper endswith the optimization design of the deep tunnel section in an effort to decrease the concentration state of nonlinear stress in tunnel base angle,with the resultant reduction ofmore than 20%in the quantity of tunnel floor heave.

surrounding rock and support;dissipation structure;reliable entropy;nonlinear

TD353

A

1671-0118(2010)02-0097-06

2010-03-11

黑龙江省科技攻关项目(GC05A307)

孙广义(1957-),男,辽宁省辽阳人,教授,博士,研究方向:采矿工程,E-mail:sgy8866@sohu.com。

(编辑晁晓筠)