上证指数市场风险度量问题研究

张留禄 王楚明

（1.上海应用技术学院，上海 2002352.上海立信会计学院，上海 201620）

经济学与经济管理

上证指数市场风险度量问题研究

张留禄1王楚明2

（1.上海应用技术学院，上海 2002352.上海立信会计学院，上海 201620）

本文通过建立收益率满足的EGARCH-t①邹建军、张宗益、秦拯：《GARCH模型在计算我国股市风险价值中的应用研究》，系统工程理论与实践2003年第5期，第20-25页。模型，分析计算了从1997年1月2日到2009年4月我国股市上证指数的市场风险价值——VaR，度量了该时期不同阶段上证指数的市场风险状况，并认为，VaR方法的运用，会在我国市场风险、信用风险管理方面起重大作用。

VaR模型 市场风险 信用风险

一、引言

自上世纪九十年代，摩根大通公开推出计算VaR的Risk Metrics风险控制模型，将“风险价值”（或“在险价值”）思想引进推广，历经十余年的实践验证，VaR模型已然发展成为被欧美、日本等金融发达国家普遍认可、权威金融和监管机构情有独钟的市场风险测度工具。1993年30G提出以风险资本（Capital-at-risk）即风险价值法（VaR）衡量风险，特别针对场外衍生工具的市场风险；1995年，SEC也发布要求美国公司采用VaR模型②龚锐、陈仲常、杨栋锐：《GARCH族模型计算中国股市在险价值（VaR）风险的比较研究与评述》，数量经济技术经济研究2005年第7期，第67-75页。作为三种可行的披露衍生交易活动信息的方法之一；尤其是在巴塞尔协议中，VaR对风险的度量作用日益显著。

1974年因为暴发的债务危机使银行业信用风险的防范与监管提到重要的议事日程上，由十国中央银行倡议建立了巴塞尔委员会，1975年9月第一个《巴塞尔协议》③王修华、黄满池：《基于新巴塞尔协议的银行操作风险管理》，《经济问题》2004年第10期 ，第59-61页。出台，提出银行接受监管和相关职责；此后巴塞尔协议几经实践检验、多次修改确立了以资本充足率、监管部门监督检查和市场纪律为三大支柱的监管框架，其中资本充足率是核心，在计算最低资本要求时，强调信用风险、市场风险和操作风险的银行三大风险。对于风险衡量方法多种多样，不过自从1995年巴塞尔委员会规定了银行使用内部模型计算风险的VaR值以来，VaR在测算风险，特别是市场风险上发挥重要作用，目前全球已有超过1000家的银行、保险公司、投资基金、养老金基金及非金融公司采用VAR方法作为金融衍生工具风险管理的手段。

VaR模型之所以独具魅力，不仅得益于其超越传统风险测度的非线性假设，如权益的β值都是以线性假设为前提的；更加体现在它的普遍适用性和对现实风险的良好拟合上。VaR模型可以应用于利率、汇率、股票、债券、期货等各种资产及资产组合的风险测度，且VaR值在不同类型的资产及组合之间具有可比性，有利于进行资本的优化配置；英国巴林银行、美国安然公司、日本大和银行、新加坡中航油等数家机构在金融风险漏洞中失败的教训告诉我们，通过VaR模型进行的市场风险①郭晓亭：《基于GARCH模型的中国证券投资基金市场风险实证研究》，《国际金融研究》2005年第10期，第55-58页。测度更符合实际情况、更易察觉巨额利润后隐藏的高风险。尤其在当前金融危机大背景下，有效风险监控、得力的金融监管备受各国政府关注，如何建立更好的风险控制体系，以及更加适合的测控模型成为学术界的热点，而VaR模型的优越性无疑决定它有更广阔的运用空间。虽然我国的金融市场风险管理刚刚起步，但是中总行和少数优秀的基金公司已经开始尝试运用VaR模型进行风险测量，可以预期中国的金融机构未来会广泛运用VaR来进行市场风险的测度，并以此进行风险管理。

二、理论模型

1.VaR模型的概念

J.P.Morgan银行将其定义为：既定头寸被冲销或重估前可能发生的市场价值最大损失的估计值；Jorion把VaR定义为：“给定置信区间的一个持有期内的最坏的预期损失”。VaR（Value at Risk）的字面解释为“处于风险状态的价值”，是指在一定持有期内按一定置信水平，给定的资产或资产组可能遭受的最大损失值。用数学式来表示：

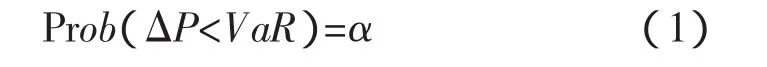
其中，Prob是计算资产价值损失小于可能损失上限的概率；ΔP表示某资产或资产组合在一定持有期的市场值的变化损益，是随机变量；α是给定的概率，即置信水平；VaR为在险价值及可能的损失上限。模型即是资产或资产组合以1-α的概率损失不会超出VaR，或者说资产或资产组合以α的概率损失超出VaR。

2.VaR的计量方法

VaR模型以市场有效性为假设前提，认为市场是随机波动的，不存在自相关。在计算风险价值法下VaR模型的时候主要有历史模拟（Historical Simulation）、方差-协方差 (Variancecovariance)和蒙特卡洛模拟（Monte Carlo）三种方法。

历史模拟法建立在资产组合的历史数据上的，以历史可以在未来重复为假设前提，根据历史数据样本的变化模拟资产组合的未来损益分布。它假设收益随时间独立分布，做出历史数据样本的频度直方图，以直方图的P-分位数作为对收益分布的波动估计，按照既定的置信水平α计算VaR值。历史模拟法没有参数，计算简便，但是面对不稳定的市场结果将产生偏差且数据收集存在困难，需要大量准确的历史数据。

方差-协方差法，即参数法，也是建立在历史数据上，假定它们服从特定的分布（一般是正态分布），估算分布参数（均值、方差、相关系数等），计算 VaR值。例如J.P.Morgan银行的Risk-Metrics方法，假设风险收益服从正态分布，采用指数加权的方式计算方差。参数法只要选择好分布模型和处理好方差，适用于预测正常、温和波动的市场，能较好地解决条件异方差等现象。不过虽然它能够进行标准差和相关系数的假设检验，但是不能检验分布假设，存在局限性。

蒙特卡洛模拟法，不同于上述两种方法，避开历史数据，通过随机的方法生成一系列数据使得模拟值包括大部分可能的情况，从而模拟资产组合风险因素的收益分布，求出VaR值。所以也称其为随机模拟方法。虽然其计算和模型实现比较慢、有难度，但是其适应波动市场和可检验性的优势使之瑕不掩瑜，近些年来在学术界赢得越来越多的青睐。

另外，关于VaR模型的还有一种风险调整的资本收益法。风险调整的资本收益（RAROC）是指收益与VaR值的比值，它反映投资的盈利风险贴现值，当从事高风险的投资项目时，即使利润再高，由于高风险导致高VaR值，RAROC值也不会很高，这样就比较客观地评价了该交易的绩效，不会出现像巴林银行、大和银行等机构由于利用传统的Delta法没有发现市场高风险，只看到某一项的高额盈利水平，无视风险漏洞的现象，避免酿成金融机构倒闭亏损的恶果。

3.VaR风险控制模型及参数计算

如果运用参数法，可以将VaR值计算定义为如下公式：

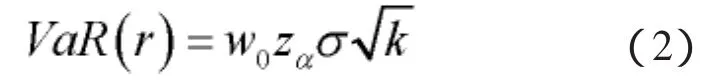
其中，r为资产收益率，w0是资产的初始价值，σ为资产收益率的标准差，k为测度期限，zα是置信度α对应的分位数，取值依赖于资产收益率的概率分布函数，不同的分布，α对应的分位数不同。资产收益率的标准差分为条件标准差和无条件标准差两种，只有条件标准差才能反映时变风险的特性。因此，为了准确估计VaR，我们面临两个问题，一是适合的分布函数，二是对资产收益率的条件标准差的估计。对于后者，前文提到的J.P.Morgan银行的Risk-Metrics方法对方差指数加权的计算方式实际上就是一种GARCH模型的应用，即方差是滞后项与过去误差的函数。GARCH模型属于ARCH族模型，其中还包括EGARCH、PGARCH及相应的均值方程（ARCH-M族）模型，国内外学者都做了大量的实证分析和研究。1992年 Robert Engle将 ARCH（Auto Regressive Conditional Heteroskedasticity Model，即自回归条件异方差模型）模型引入VaR计算中，见公式：

一般自回归条件异方差，GARCH（p，q）：

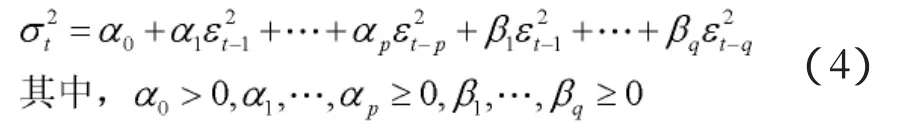
较ARCH（p）模型中增加了q个自回归项，即GARCH过程是无限阶的ARCH过程，解决了ARCH模型待估参数减少，提高了准确性。但是GARCH模型系数的非负性约束太强，且残差对条件方差的对称性影响与实际金融价格运动的杠杆效应相抵触，即下降的证券价格比上升同幅度多引发的波动更大。

指数GARCH模型是GARCH模型的一种特殊形式，能更加深刻地刻画金融时间序列方差的非对称性，EGARCH的具体表达形式如下：

对条件方差取对数，解放了GARCH模型的系数非负性约束，使模型应用更广泛。同时，引进一个新的参数γ，当γ≠0时，残差对方差非对称性，刻画出市场的杠杆效应，对金融时间序列拟合效果很好。

对于分布函数的确定，Risk-Metrics方法是假设金融资产收益序列呈正态分布，其实大量的金融实证研究表明金融资产收益具有尖峰厚尾的特征，所以我们采用t分布更加贴切，t分布的概率密度函数：

4.VaR模型的准确性检验①谷耀、陆丽娜：《沪、深、港股市信息溢出效应与动态相关性——基于DCC-（BV）EGARCH-VAR的检验》，《数量经济技术经济研究》2006年第8期，第142-151页。

考察实际损益超过在既定的置信水平下VaR值的概率是否在置信概率以内，亦作后验测试（Backtesting），指检验VaR模型的计算结果对实际损失的覆盖程度。

三、实证分析

1.模型拟合

本文选取的历史数据是1997年1月2日到2009年4月3日的上证指数，总共2959个数据，数据来源于Wind资讯。考虑股票收益波动②刘晓星、何建敏、刘庆富：《基于VaR-EGARCH-GED模型的深圳股票市场波动性分析》，《南开管理评论》2005年第5期，第11-15页。的厚尾性以及价格冲击的非对称性，模型选取EGARCH-t模型。本文计算上证指数日对数收益rt=ln（pt/pt-1），其中pt为每个交易日上海股票市场的日收盘成份指数，本文所有计算在Eviews5.0上完成。

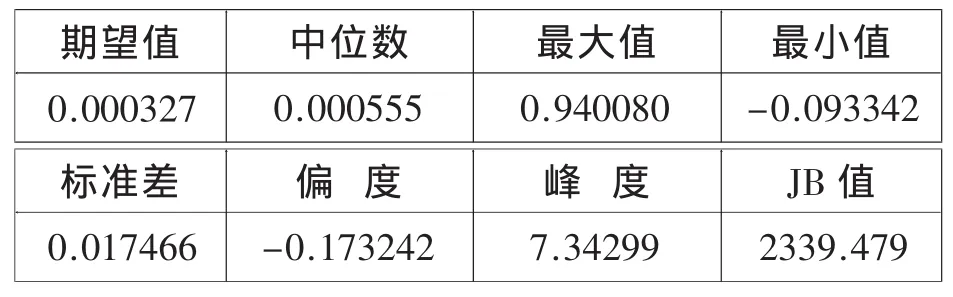
表1 上证指数日对数收益的描述性统计数据

由表1可知，偏度系数显著不为0，峰度系数远大于3，JB统计量也大于临界值5.9915，因此拒绝正态分布的原假设，对数收益率尖峰厚尾特征明显。方差方程设定为（5）式，残差满足t分布，采用极大似然估计来估计方程的各个参数。在建立GARCH族模型之前，用AIC与SIC信息准则,经过反复试算,判断滞后阶数（p，q）为（1，1）比较合适,所以运用下模型:

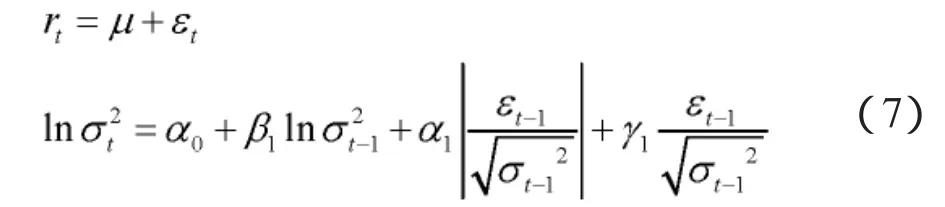
2.VaR计算以及返回检验

上证指数日对数收益VaR③胡援成、姜光明：《上证综指收益波动性及VaR度量研究》，《当代财经》2004年第6期，第34-38页。的计算有以下几个步骤：由回归得到的参数估计值，通过计算条件方差，从而得到时变的标准差，并由（2）式计算VaR，其中为股票指数的初始值，在此标准化为1元。为保证计算的精确性，本文计算了每天的VaR。表3给出了student-t分布95%和99% 置信水平下的分位数，其中t分布的分位数由数值积分得到，通过EVIEWS程序可以求出相应的分位数。根据表3的分位数，可以求出不同置信水平下两种分布的VaR值。统计结果见表4。

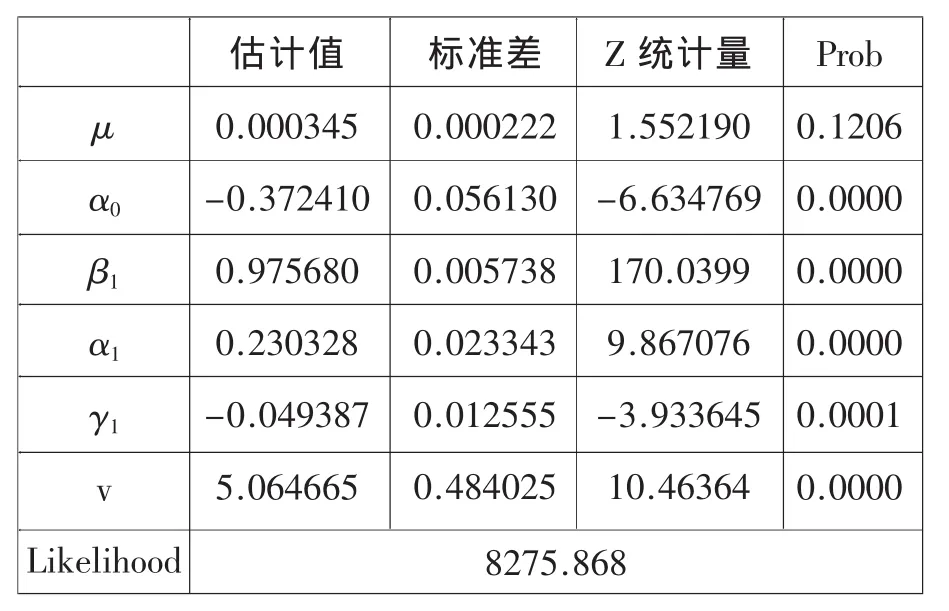
表2 上证指数日对数收益AR（1）-EGARCH（1,1）-t回归结果

表3 t分布对应于置信水平95%与99%的分位数

四、结论

本文利用EGARCH(1,1)-t模型计算了我国股市上证指数日对数收益率的VaR，研究了股票市场风险波动随时间变化的特征，探讨了股票收益和波动间的动态关系，得出了以下结论：模型对上海股票市场的波动性描述是客观的。它反映了上海股票市场的波动类聚特征、风险和收益之间的正向关系特征以及波动的杠杆效应等；表明了我国股票市场已初步呈现出国外成熟股票市场的基本特性。图1详细刻画了我国上海股市自1997年设立涨跌停板以来市场风险变化的统计特征，由图中可以看出，1997年，1999～2000年，2002年，以及2007～2009年这几个阶段，VaR值比较大。1997年，1999～2000年以及2007～2008年是因为处于中国股市的牛市阶段，股市的飙升带来了泡沫的扩大，因此市场风险也比较大；2002年，2008～2009年是由于股市由牛转熊带来的股价狂跌，市场严重受挫，因此市场风险也随之扩大。

表4 在不同置信度情况下的日VaR值统计结果及返回检验结果

图1 上证指数日线图

图2 在不同置信度情况下的日VaR值变化图

由以上分析可见，VaR在度量市场风险方面①杜平、徐济东：《用VaR度量与管理投资基金的市场风险》，《经济问题探索》2007年第7期，第67－71页。体现了重要的作用。是一种比较成熟比较实用的方法，对于检测我国股市的泡沫状况以及破灭后的影响也有一定的借鉴意义。目前，随着研究的深入和方法的推广，VaR同样可以在衡量信用风险和操作风险上发挥作用。国际流行的主要的信用风险度量模型Credit metrics,Credit risk+,Credit Portfolio View以及KMV，都是采用了VaR的方法。我们相信，VaR方法的运用，会在我国市场风险、信用风险管理方面起重大作用。

Research on the Market Risk Measure Based on the VaR Model for Chinese SSE Composite Index

ZHANG Liulu，WANG Chuming

We here analyze market Value at Risk（VaR）of Shanghai Stock Exchange Composite Index from January2nd，1997 to April3rd，2009 through building EGARCH-t-VaR model.Furthermore，we conclude the Market Risk during the same period.

t-distributed，EGARCH，VaR model

张留禄（1962-），男，河南郑州人，教授，经济学博士，上海应用技术学院劳动安全与社会保障研究所所长，河南大学硕士生导师，研究方向为金融学、社会保障学；王楚明（1963-），男，河南信阳人，教授，经济学博士，上海立信会计学院金融学院院长，华东师范大学硕士生导师，研究方向为资本理论、货币理论、金融发展理论等。

F830.91

A

1008-7672（2010）03-0048-06

余风）