基于地统计学的作物需水量空间变异性分析*

李立,魏晓妹,韩业珍

(西北农林科技大学水利与工程建筑学院,陕西杨陵712100)

作物需水量是区域灌排工程规划、设计、管理的基本依据,也是地区间水量水权分配,跨流域引水、调水决策的基础[1]。但由于受到气象条件、土壤特性和作物性状等诸多因素的影响,作物需水量在空间上存在较大的变异性,人们必须将有限的站点资料通过科学的估值方法来确定众多非测点的需水量值,进而得到区域需水量值。因此,分析作物需水量在空间上的变化规律,尽可能提高估值精度显得尤为重要。

经典统计学依赖样本频率分布或均值方差关系来确定空间分布格局和相关关系,忽略了空间位置,而地统计学既能考虑到样本值的大小,又重视样本空间位置及样本间的距离,弥补了这一缺陷[2]。近年来广泛应用于涉及空间分析的领域,作物需水量的空间分析也不例外。特别是GIS和地统计学的结合,解决了作物需水量空间分析运算繁杂的遗憾,并且实现了结果的可视化。

ARCGIS地统计分析模块在地统计学与GIS之间架起了一座桥梁,使得复杂的地统计分析方法可以在软件中轻易地实现[3]。本文尝试以陕西省宝鸡峡灌区为例,分析作物需水量的空间变异性,以期对区域灌溉制度和农业结构调整、生态建设和水资源的可持续利用提供依据。

1 作物需水量计算及数据处理

1.1 研究区概况

宝鸡峡灌区位于陕西省关中平原西部,西起宝鸡市以西的渭河峡谷,东至泾河,南临渭水,北抵渭北高塬腹地。总控制面积2 355 km2,灌溉宝鸡、咸阳、西安3市14个县(区)的19.44万 hm2农田,是陕西省最大的国有灌区。

灌区属大陆性气候的半干旱地区,年平均降水量576 mm,年平均蒸发量1 110 mm,平均气温14℃(最高43℃,最低21.5℃),日照2 140 h。灌区土壤以壤土、黄绵土及淤土等三类土壤为主,适合耕作。农作物以冬小麦、玉米、棉花为主,自开灌以来,辖区农业生产条件不断得到改善,现已成为全省的粮、油、果、蔬菜出产基地。

1.2 作物需水量计算

1.2.1 计算方法

(1)ET0的计算。计算参考作物需水量应用最多的是1998年FAO-56推荐的Penman-Monteith公式,孙景生[4]、史海滨[5]、刘钰[6]、Jensen M E[7]、Peter Droogers[8]等通过研究,均认为 Penman-Monteith方法具有较充分的理论和较高的计算精度,加之不需要进行地区率定,使用非常方便。本文利用灌区11个站点1981-2003年共23 a的日照时数、平均风速、平均相对湿度、平均最高气温、平均最低气温、降雨等月气象资料、各站点相应的海拔高度和地理纬度资料,选用Penman-Monteith法计算参考作物需水量(ET0)。

式中:ET0——参考作物需水量(mm/d);Rn——作物表面净辐射[MJ/(m2·d)];G——土壤热通量[MJ/(m2·d)];T——2 m 高度处平均气温(℃);U 2——2 m 高度处 24 h平均风速(m/s);ea——实际水汽压(k Pa);ed——平均饱和水汽压(k Pa);Δ——饱和水汽压斜率(k Pa/℃);γ——干湿球常数(k Pa/℃)。

(2)ETc的计算。根据《陕西省作物需水量及分区灌溉模式》[9]关中西部宝鸡峡灌区冬小麦、玉米和棉花的作物系数,确定Kc值,进而利用公式(2)计算各种作物的需水量(ETc)。

式中:ETc——作物需水量(mm);Kc——作物系数;——参考作物需水量(mm)。

1.2.2 计算结果 计算得到灌区冬小麦、玉米和棉花三种作物多年平均需水量(1981-2003年)如表1所示。

1.3 数据处理

通过扫描仪将纸质1∶250 000的行政地形图扫描入计算机,在 ArcMap平台上进行拼图、校准等,再将各气象站点以点文件的形式进行存储。

将各站点的海拔高度、经纬度以及表1所示的冬小麦、玉米和棉花的多年平均需水量作为属性,建立属性数据库。

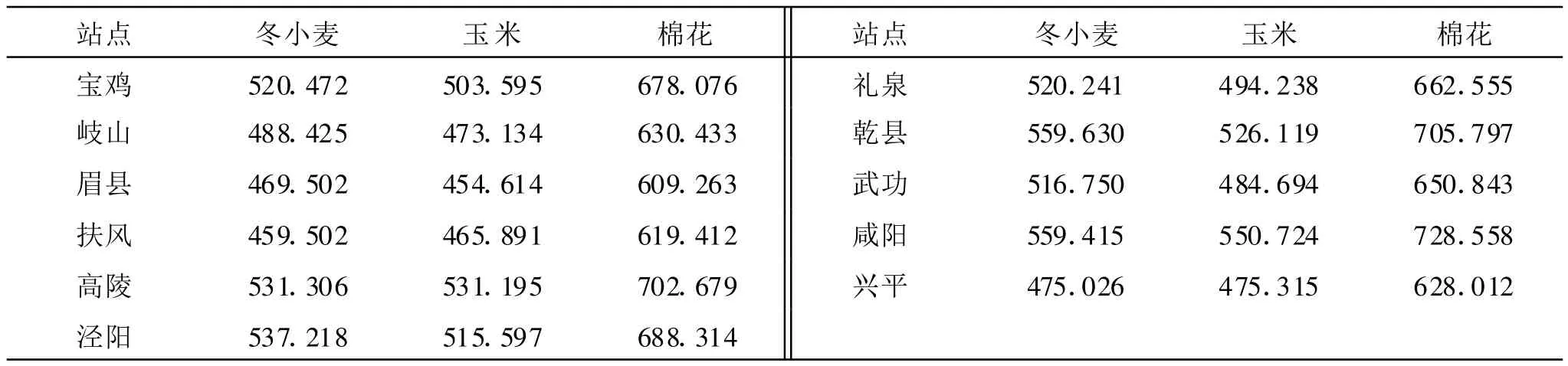
表1 灌区11个站各种作物ETc多年平均值 mm/a

2 研究方法

2.1 地统计学理论

地统计学理论基础包括前提假设、区域化变量、变异分析和空间估值[10]。一个完整的地统计分析过程为:首先获取原始数据,检查、分析数据,寻找特点和规律;然后选择合适的模型进行表面预测;最后检验模型是否合理或几种模型进行对比,确定预测模型。由于不同作物的需水量空间变化规律的分析过程和主要步骤大体相同,下面将以冬小麦为例简述其分析过程。

2.2 数据检查

灌区冬小麦多年平均需水量峰值和偏态值均接近于0,数据分布近似正态分布且稍显平坦(表2)。

表2 数据基本统计特征表

在ARCGIS 9.2的地统计模块中,做正态QQPlot分布图和趋势分析图寻找分布规律和趋势,图1中数据接近一条直线,表明它接近于服从正态分布。进一步运用半变异函数分析,发现球状模型为最优拟合方法,块金值/基台值为57.42%,在25%～75%之间,表明冬小麦需水量具有中等的空间相关性[11],变程为85.040 km,表明冬小麦需水量在较大空间范围内存在空间相关性。这是由结构性因素(辐射、温度、湿度、风速、降水等)和随机性因素(耕作措施、种植制度等)共同作用的结果。结构性因素导致空间分布的强相关性,而随机性因素使得空间相关性减弱。

半变异/协方差函数云图表示的是数据集中所有样点对应的理论半变异值和协方差,并把它们用两点间距离的函数来表示,用此函数作图来表示,如图2。

左图为无方向性的半变异/协方差函数云图,图中冬小麦作物需水量的空间自相关性不明显,右图为有方向性的半变异/协方差函数云图,由此图可以看出,冬小麦需水量在东北-西南方向空间相关性很强,初步说明作物需水量受纬度影响较大。

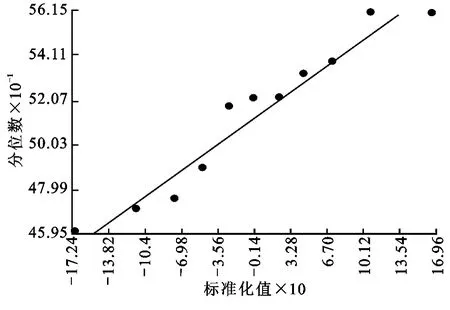
图1 数据正态QQPlot

图2 半变异/协方差函数云图

2.3 地统计插值与经典统计插值的比较

经典统计学插值方法主要是以研究区域内部的相似性、或者以平滑度为基础由已知样点来创建表面。主要有反距离权插法、径向基插法和局部多项式插值法等。

地统计学的Kriging是以变异函数理论和结构分析为基础,在有限区域内对区域化变量进行无偏最优估计的一种方法。Kriging方法有很多,其中,Ordinary Kriging是区域化变量的线性估计,它假设数据变化成正态分布,认为区域化变量的期望值是未知的,冬小麦多年平均需水量数据满足插值条件,因此选用Ordinary Kriging进行插值,并与反距离权插法进行比较分析。按需水量值等间距分成8个等级,结果如图3和图4所示。

从图3和图 4可以看出,宝鸡、眉县、扶风和礼泉、泾阳、咸阳附近插值结果很接近,在武功、兴平、乾县附近差异较大。反距离权插法误差均值为2.235,误差均方根为36.83,Ordinary Kriging误差均值为-2.228,误差均方根为33.38,平均标准误差为36.06,标准平均值为-0.057 38,标准均方根预测误差为0.942 1。通常认为,误差均值、误差均方根、平均标准误差和标准平均值小,标准均方根预测误差接近于1的插值效果较好。因此,Ordinary Kriging插值效果较理想,作为灌区冬小麦多年平均需水量插值结果。

3 作物需水量空间变异性结果分析

3.1 冬小麦需水量空间变异性分析

从图4可以看出,宝鸡峡灌区冬小麦多年平均需水量在 516.1～535.5 mm的面积最大,为

1 250.3 km2,占灌区面积的53.1%,主要分布灌区东部,乾县、礼泉、泾阳、咸阳和高陵西南部,并且从东向西呈增大趋势;在503.2～516.1 mm面积为

638.3 km2,占灌区面积的 27.1%,主要分布在武功、兴平;需水量在490.3～503.2 mm面积为466.4 km2,占灌区面积的19.8%,主要分布在灌区西部,眉县、扶风、宝鸡附近,其中眉县、扶风区域需水量最小490.3～496.8 mm。

图3 反距离权插值生成的预测面

图4 Ordinary Kringing插值生成的预测面

3.2 玉米需水量空间变异性分析

从图5可以看出,该灌区玉米多年平均需水量在483.5～505.5 mm的面积最大,为1 128.6 km2,占灌区面积的47.9%,主要分布在武功、兴平和乾县;在505.5～528.3 mm的面积为855.8 km2,占灌区面积的35.6%,主要分布在礼泉、泾阳、咸阳;需水量在454.6～483.5 mm的面积为466.4 km2,占灌区面积的16.5%,主要分布在灌区东部,以眉县东北部和扶风附近需水量最小,为454.6～475.8 mm。

图5 玉米多年平均需水量分布图

图6 棉花多年平均需水量分布图

3.3 棉花需水量空间变异性分析

该灌区棉花多年平均需水量在653.3～681.3 mm的面积为1 157.3 km2,占灌区面积的49.1%,主要分布在武功东部,乾县、兴平和礼泉西部;需水量在681.3～700.0 mm的面积为580.4 km2,占灌区面积的24.6%,主要分布在泾阳、咸阳,灌区西部宝鸡、眉县附近需水量较小,需水量在 609.2～653.3 mm,面积为 617.3 km2,占灌区面积的26.2%(图 6)。

4 结论

以宝鸡峡灌区三种主要作物的多年平均需水量为例,将地统计学和GIS结合,分析作物需水量在空间上的变化规律,体现了基于GIS的地统计分析用于大尺度作物需水量空间变异性研究的便捷性。

研究结果表明:灌区不同作物需水量差异很大,冬小麦多年平均需水量490.3～535.5 mm,玉米454.6～505.5 mm,棉花609.2～681.3 mm。但是,各种作物的多年平均需水量分布存在类似规律,均在西南-东北方向上变程较大,眉县附近达到最小,往东北方向逐渐增大。究其原因,可能与气象因子的空间变化有关,此外可能与纬度和地势有关,关于这方面的研究,有待进一步深入。

[1] 王景雷,孙景生,刘祖贵,等.作物需水量观测站点的优化设计[J].水利学报,2005,36(2):225-231.

[2] 孙英君.王劲峰.伯延臣.地统计学方法进展研究[J].地球科学进展,2004,19(2):268-273.

[3] 孙英君,王劲峰,柏延臣,等.地统计学的GIS空间分析功能扩展[J].华侨大学学报:自然科学版,2004,25(4):435-439.

[4] 孙景生,刘祖贵,张寄阳,等.风沙区参考作物需水量的计算[J].灌溉排水,2002,21(2):17-20.

[5] 史海滨,陈亚新,徐英,等.大区域非规则采样系统ET0的最优等值线图Kriging法绘制应用[C]//农业高效用水与水土环境保护.西安:陕西科学技术出版社,2000:266-271.

[6] 刘钰,Pereira L S,.Teixeirab J L,等.参照腾发量的新定义及计算方法对比[J].水利学报,1997(6):27-29.

[7] Jensen M E,Burman R D,Allen R G.Evapotranspiration and irrigation water requirement[R].ASCE manual,1990.

[8] Peter D,Richard G A.Estimating reference evapotranspiration under inaccurate data conditions[J].Irrigation and drainage systems,2002,16:33-45.

[9] 马孝义,康绍忠.陕西农林牧渔业及农村生活用水定额编制报告[R].陕西省水资源管理办公室,2004.

[10] 王政权.地统计学及在生态学中的应用[M].北京:科学出版社,1999.

[11] Cambardella C A,Moorman T B,Novak J M.Field-scale variability of soil properties in central lowa soils[J].Soil Sci Soc Am J,1994,68:1501-1511.

[12] 陈海生,曹瑛杰.基于地统计和GIS的河南省降水量和蒸发量空间变异性分析[J].河南大学学报:自然科学版,2008,38(2):160-165.