吉林省经济增长和环境变化的动态关系

高迎春，佟连军，马延吉

1.中国科学院东北地理与农业生态研究所，吉林 长春 130012 2.中国科学院研究生院，北京 100049

吉林省经济增长和环境变化的动态关系

高迎春1，2，佟连军1*，马延吉1

1.中国科学院东北地理与农业生态研究所，吉林 长春 130012 2.中国科学院研究生院，北京 100049

以吉林省为例，采用无残差完全分解方法和柯布-道格拉斯生产函数，分别提取环境变化和经济增长的驱动因子，在分析共同影响因子对环境系统和经济系统作用差异的基础上，应用异速生长模型分析经济子系统和环境子系统的相对变化关系.结果表明：经济增长和环境变化具有不同的增长维度，环境变化中的规模效应依赖于经济系统中资源要素的投入水平，而驱动经济增长的技术变化因子仅仅是引起环境变化技术效应的一个方面，环境系统的技术变化具有一定的独立性;经济增长和环境变化既有关联性也有差异性，经济系统主导形成二者倒“U”型的数量关系，而环境系统影响因子进一步决定了在何种污染程度上穿越环境高山;环境变化和经济增长的相对速率具有广义分维性质，环境系统和经济系统的负异速生长是实现可持续发展环境目标的根本途径.

经济增长;环境变化;分维;异速生长;吉林省

经济增长在推动社会物质生产大发展的同时，也暴露出了许多负面效应，环境污染和生态环境恶化等已经对人类的生存和发展构成了严重威胁，区域发展正面临着发展经济和保护环境的双重任务［1］.环境库兹涅茨曲线(EKC)假设反映了经济增长与环境质量之间倒U型的曲线关系［2］，从宏观尺度上为研究经济增长和环境质量的关系提供了有益的经验性探索［3］.对此，国内外学者依据各类环境数据，采用不同数理模型［4］，在不同地区尺度上对EKC的有效性、应用和测度进行了大量研究［5］，但并未达成一致性结论［6］，一些实证分析并不支持EKC假设［7-9］.也有学者认为，EKC本质上是一种经验现象［10］，而不是一个必然规律［11］.针对环境库兹涅茨曲线在描述经济增长与环境质量关系时的不足，GROSSMAN［12］将环境质量的变化分解为规模效应、结构效应和技术效应，有助于揭示环境压力和不同驱动因子之间的关系，以及进一步探索经济增长对环境变化的作用过程.笔者在认识环境变化驱动因子和经济增长驱动因子的基础上，对比环境系统和经济系统的变化维度，以及相应驱动因子的作用差异，进而应用异速生长模型从经济-环境系统整体视角分析经济系统和环境系统的相对变化关系，以期为认识经济增长与环境变化的相互关系，指导环境保护政策的制定和实施提供科学依据.

1 环境变化影响因子

1.1 数据来源

以吉林省9个市州为地区单元，选用地区生产总值(2000年不变价)表示经济规模;污染治理成本在一定程度上可以反映经济发展对环境质量的影响程度，以工业二氧化硫、工业烟尘、工业粉尘、工业废水和城镇生活污水中COD等5类污染物的排放量作为基础数据，依照我国《排污费征收标准管理办法》附件《排污费征收标准及计算方法》中关于各类污染物的折算系数和当量收费标准，分类计算污染物的污染当量数，并按照当量收费标准换算为排污费，加和汇总后反映各地区环境质量水平.基础数据源于相应年份的《吉林省环境质量报告书》和《吉林统计年鉴》.

1.2 环境变化效应分解

完全分解模型将残差项中忽略的影响效果精确分配到计算结果中，消除了分解结果中的估计误差［13］.根据完全分解模型计算公式［14］，将 2000—2007年吉林省历年及分时段的环境变化(△W)分解为经济规模(Q)、经济空间结构(S)和排污强度(I)影响下的3种不同变化效应，即规模效应(WQ)、结构效应(WS)和技术效应(WI)，结果见表1.

1.3 环境变化影响因子分析

环境变化主要受到经济总量及其增长速度、产业结构及其变化幅度、排污强度及其进步水平的影响，并以规模效应、结构效应和技术效应的形式表现.由表1可知，规模效应均为正值，发挥增量作用;技术效应在多数时段中为负值，主要表现为减量作用;而结构效应增减作用差异较大，作用趋势并不明显.从相关性来看，规模效应和经济总量变化的相关系数为0.961，且在0.01水平上通过显著性检验，规模效应的增量作用主要源于经济增长.结构效应和技术效应与环境变化总量的相关系数分别为0.826和0.936，分别在0.05和0.01水平上通过显著性检验，环境变化趋势主要受到技术效应和结构效应的影响.

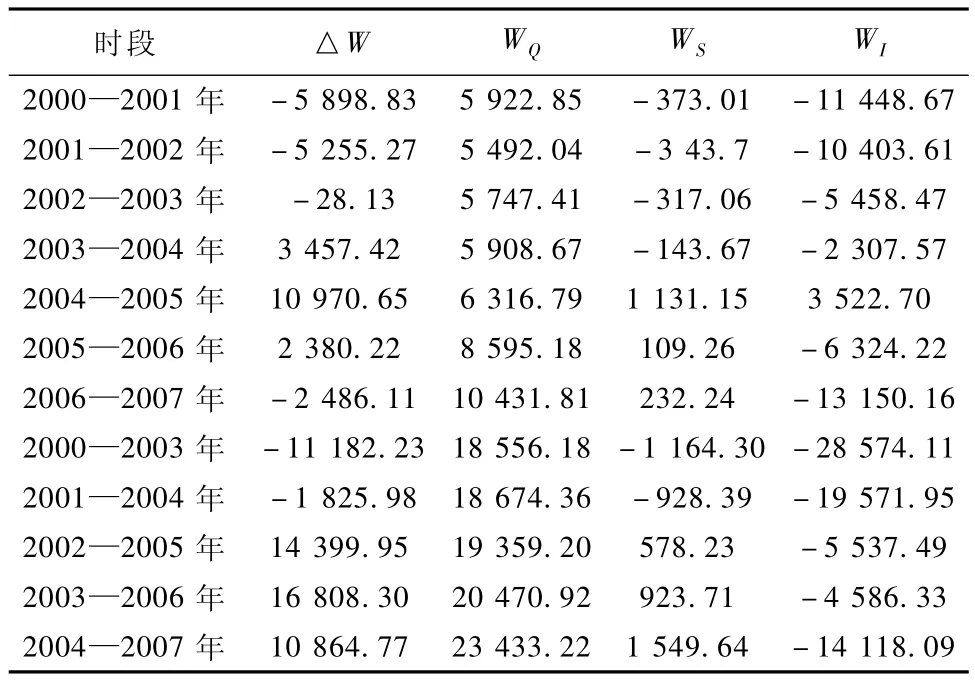
表1 环境变化效应分解Table 1 Effect decomposition of environmental changes 104元

弹性反映了随自变量的变化因变量变化幅度的大小，也是因变量对自变量变化反应的强烈程度或灵敏度［15］.引入环境变化弹性的概念，进一步分析单位经济增长引发的环境变化，以及不同分解组分对经济变化的敏感性.由图1可知，规模效应弹性大于0，技术效应弹性在多数年份都小于0，而结构效应弹性在0附近波动，经济增长主要通过规模效应和技术效应作用环境变化.环境变化总量弹性和环境变化总量的相关系数为0.954，结构效应弹性和结构效应的相关系数为和0.994，二者都在0.01水平上通过了显著性检验.环境变化总量和结构效应对经济增长的反应较为平缓.规模效应弹性和规模效应的相关系数为-0.687，技术效应弹性和技术效应的相关系数为0.645，二者均未通过显著性检验，弹性变化和绝对量变化发生较大偏离.规模效应和技术效应对经济增长较为敏感，环境变化总量弹性主要受到规模效应弹性和技术效应弹性的影响.变化幅度以技术效应最大，规模效应和结构效应较小，对比之下技术效应具有较强活力，可望在降低环境污染方面发挥更大作用.值得注意的是，规模效应变化和规模效应弹性变化方向相反，也从另一侧面反映了经济变化对于规模效应的影响.

图1 环境变化分解及其弹性对比Fig.1 Decomposition of environment changes and their elasticity

2 经济增长驱动因子

2.1 数据来源

鉴于经济增长模型中以资源、资本、劳动作为3个要素投入已为众多学者所采用［16］，故笔者以在岗职工工资总额为劳动投入;以固定资产投资为资本投入;以全年用电量按1元/(kW·h)折算后值为资源投入;以地区生产总值(2000年不变价)为经济产出.为缩小各决策单元间因辖区规模等带来的影响，采用人均投入和人均产出作为最终取值.基础数据来源于2001—2008年的《吉林统计年鉴》.

2.2 经济增长分量构成

借鉴柯布-道格拉斯生产函数(Cobb-Douglas Production Function)和 Malmquist指数模型，计算不同生产要素生产率及全要素生产率(TFP)，以此反映不同驱动因子对经济增长的作用差异.对柯布-道格拉斯生产函数两侧同时取对数，建立劳动、资本和资源3种生产要素与地区生产总值的多元回归模型，可得：

式中，y为经济产出，104元;x1，x2，x3分别为劳动要素(104元)、资本要素(104元)和资源要素(104元);a为生产效率系数;α，η，γ分别为劳动要素、资本要素和资源要素投入的弹性系数，反映单位生产要素投入产生的经济产出增减幅度;μ为干扰项.ln a与μ的和大致对应于索洛意义上的 TFP.采用Malmquist指数识别 TFP变化，其包括技术变化(TC)和效率变化(EC)［17］，其中效率变化又可分为净效率变化(PEC)和规模效率变化(SEC)［18］.

为增加统计样本数量，以吉林省各市州为样本单元，选用 2000—2003年，2001—2004年，2002—2005年，2003—2006年，2004—2007年 5组数据分别进行回归，通过不同组别间相应回归系数的差异反映全要素生产率与单要素生产率的变化，回归结果(见表2)显示式(1)的拟合度较好，模型和系数在0.05水平都通过了显著性检验.对2000—2007年包括市州和全省在内的10个决策单元进行Malmquist指数计算［19］，获得效率变化、技术变化、净效率变化、规模效率变化和TFP变化 (见表3).

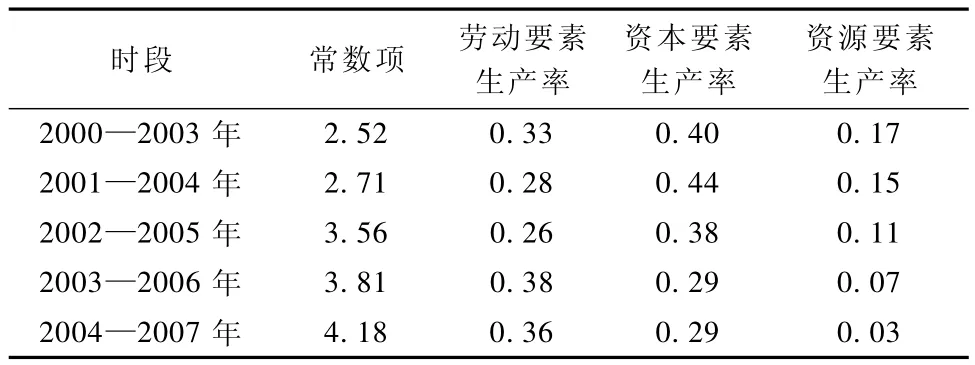
表2 各组方程回归系数Table 2 The coefficients of regression equations

2.3 经济增长驱动因子分析

经济增长的驱动因子主要为劳动、资本、资源等生产要素生产率和全要素生产率.从表2来看，全要素生产率(对应于常数项)呈上升态势，增幅较大;劳动要素生产率先下降再上升，波动性较大;资本要素生产率趋向下降，也说明在投资拉动战略背景下，资本要素对吉林省经济增长的制约得以缓解;而资源要素对经济增长的影响呈下降态势，变化较为规律，区域经济增长去物质化初显成效.全要素生产率的进步依赖于生产前沿面的推进，以及实现生产前沿面的组织、管理、协作水平的提高.技术变化和效率变化在很大程度上取决于资本投入和劳动者素质的质量.效率变化和技术变化的相关系数与劳动要素生产率和资本要素生产率的相关系数较为相近，且二者都在0.05水平上通过显著性检验，也从侧面反映了效率变化与劳动要素生产率变化，以及技术变化与资本要素生产率变化的对应联系.对比之下，资源要素投入与其他经济增长驱动因子的联系较弱.

表3 TFP及其分解组分变化Table 3 Changes of TFP index and its decomposition fractions

由表3可知，除2001—2002年外，其余年份全要素生产率都大于1，呈上升趋势，而效率变化和技术变化表现出较大波动.从相关性上来看，全要素生产率变化与技术变化和效率变化的相关系数都较低;技术变化和效率变化为负相关，且在0.01水平上通过显著性检验;效率变化与净效率变化呈正相关，在0.05水平上通过显著性检验.由此可见，全要素生产率变化主要受到技术变化和效率变化的共同作用，而效率变化主要受到净效率变化的驱动，规模效率变化的影响作用较小.从方差来看，全要素生产率变化历年差异最小，而效率变化和技术变化的差异相近，二者相乘并没有造成全要素生产率变化差异的进一步扩大，表现出一定的相互补偿作用.

3 经济增长与环境变化影响因子对比分析

经济增长和环境变化有着不同的影响因子，也决定了经济系统和环境系统在增长维数和变化途径方面的差异.为进一步认识经济增长和环境变化的关系，将经济增长和环境变化作为生产活动中2种不同的产出结果，通过共同影响因子建立经济系统和环境系统之间的联系，并以共同影响因子的不同作用方向来细致刻划经济增长对环境变化的作用关系.

经济发展需要更多的资源投入，从而会推动污染物排放量的增长.但是，资源要素对单位经济增长的贡献率(即弹性系数)呈下降趋势，提高资源效率，将使由单位经济增长引发的环境变化规模效应呈缩减趋势.资源要素贡献率和规模效应弹性呈较强的正相关性，相关系数为0.970，且在0.01水平上通过显著性检验，表明规模效应的变化更依赖于资源投入水平，取决于经济发展的减物质化效果.

结构效应主要通过作用生产要素组织方式来影响环境变化，其作用机制可以对应于全要素生产率中的效率变化.研究发现，结构效应与效率变化和净效率变化的相关系数分别为0.010和0.524，均未通过显著性检验，与规模效率变化的相关系数为-0.702，且在0.05水平上通过显著性检验.可见，规模经济有利于降低环境污染.由于净效率变化的影响因素较为复杂，短期内环境变化的结构效应可以进一步归因为产业发展的专业化和规模化.

全要素生产率中技术变化与环境变化技术效应的相关系数为0.465，未通过显著性检验.环境变化技术效应的主要影响因子为排污强度(环境产出与经济产出的比值)，可以分解为单位资源的环境产出与单位资源的经济产出的比值.由此可见，单位经济产出对应的环境产出不仅依赖于资源的经济效率，还取决于单位资源的环境产出，作为经济增长驱动因子的技术变化仅仅是引起环境变化技术效应的一个方面，二者并不具有直接的对应性，环境系统的技术变化具有一定的独立性.在单位资源环境产出不变的条件下，随着资源要素生产率的提高，单位经济产出对应的环境产出呈降低趋势，单位经济增量引发的环境变化技术效应仍然可能出现负值，在减量效应大于增量效应的同时驱动环境库兹涅茨曲线越过拐点.从物质流角度来看，生产活动中的物质投入与物质输出遵从质量守恒定律，随着废物的减量化、再利用和资源化，其排放量相应降低，这样资源在生产过程中的经济产出和环境产出双向分离也就成为经济系统驱动环境污染呈倒“U”型走势的直接依据.

从资源要素的贡献度和环境变化的规模效应，以及技术变化和技术效应的对应关系来看，经济产出与环境产出的关系符合环境库兹涅茨曲线走向.但是，倒“U”型曲线仅仅是经济增长和环境变化比例关系的反映，污染排放量的根本降低并不能从单一的经济系统内部得到答案，实现环境目标需要统筹利用、充分发挥经济系统和环境系统不同驱动因子的积极作用.经济系统与环境系统具有关联性，在一定范围内经济系统中的技术变化在促进经济增长的同时也推动了环境污染排放的降低.经济系统与环境系统也存在着差异性，环境系统除受到经济系统的影响外，在技术方面还表现出一定的独立性.应注意的是，被动性并不是环境系统的全部特征，通过对经济系统的反馈作用还可以表现出其主动性的一面，经济系统主导形成倒“U”型的数量关系，而环境系统影响因子进一步决定了在何种污染程度上穿越环境高山，及越过拐点后环境质量如何持续改善.经济系统和环境系统相互作用、相互影响形成复杂的耦合系统，二者具有统一性，经济增长降低环境污染并不是必然性趋势，实践中的环境库兹涅茨曲线目标需要经济系统和环境系统的共同努力.

4 经济和环境的异速生长分析

4.1 经济-环境系统的分维特征

1.3 节引入了环境变化弹性系数来定量描述经济变量波动时对环境产出的影响的敏感程度.比较分维和弹性的表达式，可以发现弹性具有分维的性质［20-21］.由于驱动因子构成及作用方式的差异，经济增长和环境变化的速率也不相同.在理论上可认为，系统要素的广义维数之比在原则上等于它们的相对增长率之比，只要标度因子不为整数或整数之比，就可认为系统具有分形性质［22］.

4.2 经济和环境的异速生长

将经济系统和环境系统看作是经济-环境耦合系统的2个子系统，应用异速生长法则可为理解经济产出和环境产出之间的相对增长关系提供更为有效的判断.若视环境污染排放量(P)为尺度，其相对增长速率为ai;经济产出(Y)为相应的测度，其相对增长速率为 aj，则有［23］：

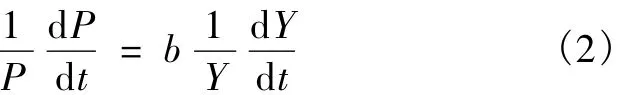
式(2)表示Y的相对增长速率和P的相对增长速率比为一常数 b［24］.对式(2)等式两边积分，即可得到异速生长方程的一般形式［25］：

式中，β为比例系数;b为标度因子，可以认为其具有广义的分维特征.

关于异速生长方程的讨论，主要集中在对标度因子(b)和比例系数(β)值的方面.在假定P和Y之间是等维度的情况下，b的含义较为明确：b＞1，正异速生长;b＜1，负异速生长;b=1，同速生长;b=0，表明P对Y的变化没有影响.以b*作为标度因子的标准值，在异速生长分析中对维度差异起到平衡作用，其含义是假设P变化是在i维空间上进行，而Y是在j维空间上增长，为平衡P和Y之间维度的不相等，b*应取值为i/j来确定同速生长情况下与Y的增长相对应的P的变化［24］.在标度因子相同或相近时，且Y取值也相同时，比例系数(β)用于不同时期的P的比较分析，可以表示为：

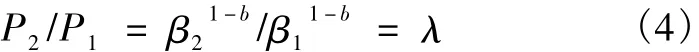
式(4)表示 P2(后一时期)为 P1(前一时期)的 λ倍［24］.

将异速增长方程两侧同时取对数，可得：

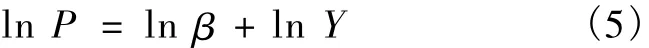
依照式(5)对经济产出和排污费按时间分组进行回归，求取比例系数和标度因子.各组方程拟合度较好，模型和系数在0.05水平均通过了显著性检验，回归结果见表4.

表4 异速生长方程回归结果Table 4 Coefficients of allometric growth equations

4.3 经济-环境系统变化动态分析

根据环境变化和经济增长的维度和作用方式，可以确定标度因子的标准值(b*)小于1，但是具体取值仍需进一步研究.选择2000—2007年组别的标度因子取值作为标准值(b*).由表4知，以2002—2004年为分界，标度因子(b)呈先下降再上升的趋势，说明投资拉动战略的实施促进了吉林省经济的快速发展，但是也造成了环境持续退化，污染治理并没有在自身维度上得到应有重视，环境建设相对滞后.与标度因子的标准值(b*)进一步对比发现，2002—2004年，2003—2005年和 2004—2006年3个组别的标度因子均小于标准值，表明期间环境系统和经济系统为负异速生长，环境产出增长速率小于经济产出增长速率，而其他组别为正异速生长.与标度因子变化相反，比例系数(β)以2002—2004年组别为界表现出先上升后下降的趋势.尽管标度因子差异较大，比例系数(β)在后期的逐步上升在一定程度上也反映了投资拉动战略的积极作用，即相同经济产出产生的污染排放，后一时期比前一时期的要少.

经济增长和环境变化具有不同的增长维度，经济增长驱动因子对经济系统主要为正向作用，对环境系统的影响则可分为扩张力因子和收缩力因子，而环境系统内部的技术因子可抑制环境退化.根据异速生长方程，未来环境变化不仅受到经济规模增长的影响，而且还依赖于标度因子(b)和比例系数(β)，同速生长并不能从根本上协调经济发展和环境退化的矛盾.因此，只有充分释放环境系统自身的活力，积极发挥环境变化影响因子的负向作用，推动环境系统和经济系统的负异速生长才能实现可持续发展的环境目标.

5 结论

a.环境变化的影响因子可以分为经济总量、产业结构和污染产出水平，经济增长的驱动因子主要为生产要素生产率和全要素生产率.环境系统和经济系统具有不同的增长维度.

b.环境变化中规模效应的变化依赖于经济系统中资源的投入水平，而驱动经济增长的技术变化因子仅仅是引起环境变化技术效应的一个方面，二者并不具有直接的对应性，环境系统的技术变化具有一定的独立性.

c.经济增长和环境变化既有关联性也有差异性，经济系统主导形成倒“U”型的数量关系，而环境系统影响因子进一步决定了在何种污染程度上穿越环境高山，及越过拐点后环境质量如何持续改善.

d.环境变化和经济增长的相对速率具有广义分维性质，表现出异速生长的特征.在实践中，推动环境系统和经济系统的负异速生长是实现可持续发展环境目标的根本途径.

［1］ 刘鸿亮，曹凤中.21世纪经济与环境协调发展全新思维模式的建立［J］.环境科学研究，2006，19(4)：148-153.

［2］ 李红莉，王艳，葛虎.山东省环境库兹涅茨曲线的检验与分析［J］.环境科学研究，2008，21(4)：210-214.

［3］ 范俊韬，李俊生，罗建武，等.我国环境污染与经济发展空间格局分析［J］.环境科学研究，2009，22(6)：742-746.

［4］ CAVIGLIA-HARRIS JL，CHAMBERSD，KAHN JR.Taking the“U”out of Kuznets：a comprehensive analysis of the EKC and environmental degradation［J］.Ecological Economics，2009，68(4)：1149-1159.

［5］ THEOPHILE A，FRANCOIS L，PHU NGUYEN V.Economic development and CO2emissions：a nonparametric panel approach［J］.Journal of Public Economics，2006，90(6/7)：1347-1363.

［6］ MERLEVEDE B，VERBEKE T，DE CLERCQ M.The EKC for SO2：does firm size matter［J］.Ecological Economics，2006，59(4)：451-461.

［7］ VICTOR B，ROBERT W M，FENG X.Health benefits of tunneling through the Chinese environmental Kuznets curve(EKC)［J］.Ecological Economics，2008，66(4)：674-686.

［8］ LUZZATI T，ORSINI M.Investigating the energy-environmental Kuznets curve［J］.Energy，2009，34(3)：291-300.

［9］ PERMAN R，STERN D I.Evidence from panel unit root and cointegration tests that the Environmental Kuznets curve does not exist ［J］.Australian Journal of Agricultural and Resource Economics，2003，47(3)：325-347.

［10］ STEM D I.Therise and fall of the environmental Kuznets curve［J］.World Development，2004，32(8)：1419-1439.

［11］ 赵云君，文启湘.环境库兹涅茨曲线及其在我国的修正［J］.经济学家，2004(5)：69-75.

［12］ GROSSMAN G.Pollution and growth：what do we know［M］//GOLDIN I，WINTERSA.The economics of sustainable development.Cambridge：Cambridge University Press，1995：19-46.

［13］ SUN JW.Changes in energy consumption and energy intensity：a complete decomposition model［J］.Energy Economics，1998，20(1)：85-100.

［14］ 李名升，佟连军，仇方道.工业废水排放变化的因素分解与减排效果［J］.环境科学，2009，30(3)：707-712.

［15］ 胡誉满，李勇红.经济弹性函数的几何解释［J］.大学数学，2003，19(4)：6-9.

［16］ 郑照宁，刘德顺.考虑资本、能源、劳动投入的中国超越对数生产函数［J］.系统工程理论与实践，2004(5)：51-54.

［17］ FARE R，GROSSKOPF S，LINDGREEN B，et al.Productivity changes in Swedish pharmacies 1980-1989：a nonparametric Malmquist approach［J］.Journal of Productivity Analysis，1992(3)：85-101.

［18］ FARE R，GROSSKOPF S，NORRISM，et al.Productivity growth，technical progress and efficiency change in industrialized countries［J］.American Economic Review，1994，84(1)：66-83.

［19］ 原毅军，刘浩，白楠.中国生产性服务业全要素生产率测度：基于非参数 Malmquist指数方法的研究［J］.中国软科学，2009(1)：159-167.

［20］ 黄登仕，李后强.分形维数与经济弹性：从线性经济学到非线性经济学的一种可能途径［J］.数量经济技术经济研究，1989，27(12)：54-56.

［21］ 司马则茜，蔡晨，李建平.我国银行操作风险的分形特征［J］.中国管理科学，2008，16(1)：42-47.

［22］ 吴丽，杨保杰，吴次芳.中国城市人口、土地和产值的分维关系研究［J］.技术经济，2008，27(4)：50-57.

［23］ 张小民，吴群琪.公路规模：经济产出的分形理论模型［J］.中国公路学报，2008，21(1)：106-111.

［24］ 李郇，陈刚强，许学强.中国城市异速增长分析［J］.地理学报，2009，64(4)：399-407.

［25］ 韩文轩，方精云.幂指数异速生长机制模型综述［J］.植物生态学报，2008，32(4)：951-960.

Study on Dynam ic Relationship between Econom ic G row th and Environm ental Change：A Case Study of Jilin Province

GAO Ying-chun1，2，TONG Lian-jun1，MA Yan-ji1
1.Northeast Institute of Geography and Agroecology，Chinese Academy of Sciences，Changchun 130012，China 2.Graduate University，Chinese Academy of Sciences，Beijing 100049，China

Applying the methods of the non-residual decomposition model and Cobb-Douglas production function，the factors driving environmental changes and economic growth were extracted.The allometric grow thlaw was used to analyze therelative dynamic relationship between economic and environmental subsystems in Jilin Province based on the analysis of the differences in the effects of factors on environmental and economic systems.Theresults showed that economic growth and environmental changes presented different growing dimensions.The scale effects on environmental changes depended on the inputlevel of resource elements in econom ic systems.The technical factor driving economic growth was only one of the factors preventing environmental deterioration，and the technical change of environmental system was independent to a certain extent.There were both correlations and differences between econom ic growth and environmental changes.Economic systems resulted in areverse“U”quantitativerelationship between economic growth and environmental changes，while environmental factors determined on which pollutionlevel environmental systems could get across the“environmentalmountain”.Therelativerate of environmental changes and economic growth was characterized by a generalized fractal dimension.The negative allometric grow th between environmental changes and economic growth is the fundamental way to achieve the objective of sustainable development.

economic grow th;environmental change;fractal dimension;allometric growth;Jilin Province

X22

A

1001-6929(2010)03-0371-06

2009-09-15

2009-11-16

吉林省科技发展计划项目(20090602);中国科学院知识创新工程重要方向项目(KZCX2-YW-342-2);中国科学院东北地理与农业生态研究所学科前沿领域项目(KZCX3-SW-NA3-20)

高 迎 春 (1978 - )， 男， 山 西 繁 峙 人，yingchun_gao@126.com.

*责任作者，佟连军(1960-)，男，吉林长春人，研究员，硕士，主要

从事环境与发展研究，tonglj@neigae.ac.cn

(责任编辑：孙彩萍)