混合量子-经典方法计算电荷转移速率及其在实际体系中的应用

南广军 郑仁慧 史 强,* 帅志刚

(1中国科学院化学研究所,分子动态与稳态结构国家重点实验室,北京分子科学国家实验室,北京 100190; 2哈尔滨工业大学基础与交叉科学研究院理论与模拟化学研究所,哈尔滨 150080; 3中国科学院化学研究所,有机固体院重点实验室,北京分子科学国家实验室,北京 100190;4清华大学化学系,北京 100084)

Considerable progresses have been made recently in methods to rigorously calculate quantum dynamics in multi-dimensional systems[1-5].However,applications of these exact methods are still limited,and approximate methods are of great interest.In particular,various mixed quantum-classical methods have been developed.The strategy of the mixed quantum-classical methods is to describe the slow nuclear dynamics by classical mechanics while retaining quantum description for the fast electronic(or light weighted atomic)degrees of freedom(DoFs).Equations of motion for the quantum and classical DoFs are coupled together: the motion of the classical DoFs results in a time-dependent quantum Hamiltonian,while at the same time,evolution of the quantum DoFs alters the forces acting on the classical ones.A critical challenge in developing mixed quantum-classical methods is to properly treat the coupled motion of the quantum and classical DoFs.Different approaches have been developed to simulate the mixed quantum-classical dynamics,among which the most commonly used methods are the Ehrenfest method[6-8], the surface hopping(SH)method[9-16],and the more recently developed mixed quantum-classicalLiouville(MQCL)method[17-22].

In both the Ehrenfest and SH methods,dynamics of the quantum subsystem is propagated fully coherently under the influence of a classical trajectory,which is sampled from a classical or quasi-classical initial distribution.However,the back-reaction to the classical dynamics is treated differently in these two methods.In the Ehrenfest method,the classical DoFs evolve on a mean field potential energy surface calculated from the expectation value of the electronic-nuclear potential energy with respect to the time-dependent quantum wave function.In the SH method,the classical DoFs move on a fixed potential surface at a given time,with localized(instantaneous)transitions between different potential surfaces using a transition probability determined by the motion of the quantum subsystem.In the MQCL method,the mixed quantum-classical dynamics is first formulated in the form of coupled Liouville equations,various propagation schemes are then designed to simulate the dynamics of these phase space equations.

All these methods have been applied to wide ranges of problems.An interesting and often overlooked problem is the validity of these methods in specific kinds of applications.Berne and coworkers have investigated the applicability of the mixed quantum-classical approaches in calculation of relaxation rate constants[23-25]and vibronic spectra[26-27].In this paper,we perform similar studies in the charge transfer rate calculations by first explicitly deriving the rate constants from the Ehrenfest,SH,and MQCL methods,and then applying them to calculate charge transfer rates in organic semiconductors.The nonadiabatic limit is considered in this study since exact results can be obtained and compared with the mixed quantum-classical approaches.Charge transfer process in organic semiconductors has attracted much theoretical attentions in the emerging field of organic electronics[28-30].We will show that the Ehrenfest and SH methods may fail when high frequency modes are involved,and should be used with caution.The remaining parts of the article are organized as follows.In Sec.1,we present the model Hamiltonian and derive the charge transfer rate expressions in the nonadiabatic limit using the Ehrenfest,SH(in the diabatic representation,see Sec.1.2), and MQCL methods.Numerical results for realistic examples of charge transfer rates in organic semiconductor materials are presented in Sec.2.The reason that the Ehrenfest and SH results deviate from the correct ones is also analyzed.The conclusions are made in Sec.3.

1 Theory

We will consider the spin-boson(SB)Hamiltonian[31-32]as a simple model to study charge transfer reactions.The total system and bath Hamiltonian is written as

where σxand σzare the Pauli matrices,Δ is the electronic matrix element that couples the donor state｜1〉and the acceptor state｜2〉,ε is the energy difference between the two states.HBand HCare the bath Hamiltonian and the system-bath coupling Hamiltonian,respectively,and can be written as

Here,pjand xjare the jth mass-weighted nuclear normal momentum and coordinate,respectively,ωjis the frequency of the jth normal mode and cjis the coupling coefficient between the charge and the jth nuclear normal mode.The essential property of the harmonic bath is characterized by its spectral density J(ω), which is defined as

where ω is electric frequency.The reorganization energy λ can be calculated from J(ω)as

To calculate the charge transfer rates,we assume that the initial state is equilibrated on the donor state ρ0=e-β(HB-HC)/Z1⊗｜1〉〈1｜, where Z1=Tre-β(HB-HC).β=1/(kBT),kBis the Boltzmann constant and T is temperature.We will also consider the nonadiabatic limit where Δ is small,such that,during the establishment of the rate dynamics,the charge population on the donor state is almost unchanged,and a perturbation treatment of Δ can be applied.In the following subsections,we will derive the charge transfer rates for the Ehrenfest,SH,and MQCL methods by treating only the electronic DoFs quantum mechanically.

For both the Ehrenfest and SH methods,dynamics of the quantum subsystem is governed by a time-dependent Hamiltonian that depends on the classical DoFs.We expand the wave function of the quantum subsystem｜ψ(t)〉as

where a1(t)and a2(t)are the complex-valued expansion coefficients.It is convenient to use the density matrix notation by defining Sx(t)=a1(t)a2(t)*+a1(t)*a2(t),Sy(t)=-i[a1(t)*a2(t)-a1(t)a2(t)*], Sz(t)=a1(t)a1(t)*-a2(t)*a2(t),where Szis the population difference between state｜1〉and state｜2〉,Sxand Syare two times of the real and imaginary parts of the coherence term between the two states,respectively.The equations of motion can now be written as(for simplicity,we have assumed that ħ=1 throughout the paper)

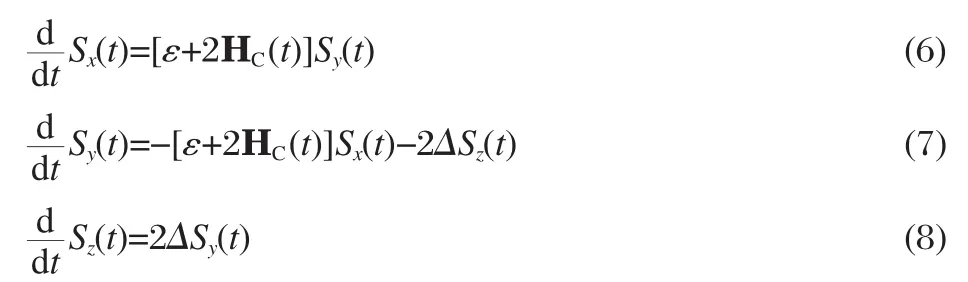
1.1 The Ehrenfest method

In the Ehrenfest method,the nuclear potential energy function that determines the classical dynamics is the expectation value of the electronic-nuclear potential energy with respect to the electronic wave function,

The simultaneous propagation of Eqs.(9-10)and Eqs.(6-8) defines the Ehrenfest method for the SB model.As we have assumed that the initial state is on the donor state,Sx(0)=Sy(0)=0 and Sz(0)=1.In the weak coupling limit and at short time,Sz(t)≈1, and we have

xj(t)can then be solved from Eqs.(9)and(11)

where xj0and pj0are the initial coordinate and momentum of the jth bath mode.

Dynamics of the quantum DoFs can also be calculated analytically.It can be shown that the following equation now provides the solution to Eqs.(6-8)

such that

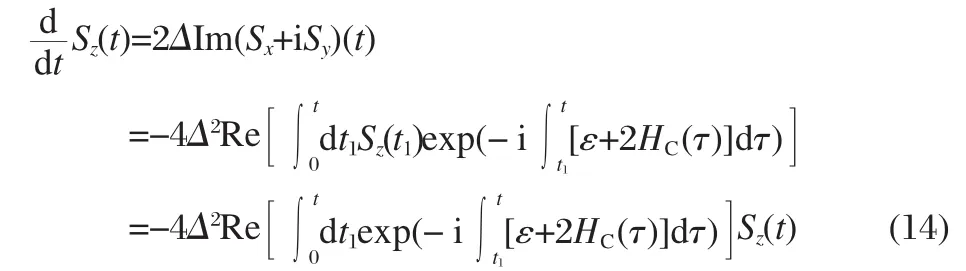
The dynamics of the quantum system can be obtained by averaging over mixed quantum-classical trajectories.

Now we define P1(t)as the population on the donor state.Since P1(t)≈1 at short time,we can obtain from Eq.(14)that

where the time dependent rate constant k(t)is as follows,

Here,the average is taken over the initial probability distribution of the classical DoFs.As time increases,k(t)reaches a plateau, and the electronic dynamics can be described as a rate process. The charge transfer rate can then be obtained by taking t→∞in Eq.(16),when also using the stationary property of HC(t),

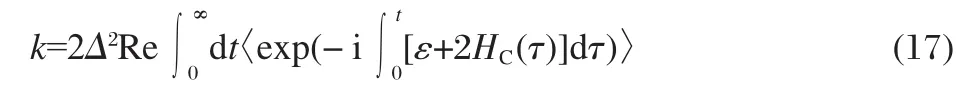
We will use the Wigner transformed distribution to include the quantum effects in the initial sampling[33-36],which is important to account for the quantum zero-point motion for high frequency modes.Since the initial distribution is assumed to be the thermal equilibrium on the donor state,it can be calculated as

where x0=(x1,x2,…)Tand Δx=(Δx1,Δx2,…)Tare column vectors, respectively.Using the above Eqs.(17-18),

It should be noted that in calculating linear absorption spectra[25-27],the mixed quantum-classical result can be obtained by taking the classical limit of the full quantum formula.Although a similar route may also be taken here,our derivation above is more direct from the mixed quantum-classical equations when considering the static quantum effects described using the initial distribution Eq.(18).

1.2 The surface hopping method

In the SH calculations presented below,the diabatic representation is used.Although the adiabatic representation was often found to be superior in many applications[16],in the case of the nonadiabatic limit for the SB model,the small coupling Δ will cause singularity for the coupling vectors in the adiabatic representation.Instead,the diabatic representation becomes more convenient.

The equations of motion for the nuclear DoFs on the two different surfaces are found to be

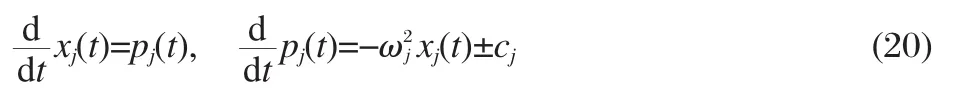
where+(-)is used for dynamics on the donor(acceptor)surface.

In the SH method,dynamics of the classical DoFs hops between different electronic surfaces.Different hopping algorithms have been proposed in the literature,among which the“fewest switches”algorithm,suggested by Tully[10,16]has been widely used. According to this algorithm,the probability per unit time of a hop from quantum state｜1〉to state｜2〉is given by

Dynamics of the quantum DoFs is the same as that in the Ehrenfestmethod,so we can applyEq.(16)to calculate k(t)forthe SH method.The only difference here is that HC(τ)is now calculated along a“hopping”trajectory that switches between donor and acceptor states.After a short relaxation time,k(t)will reach a plateau,which allows us to calculate the charge transfer rate from the SH method by taking t→∞.

From Eq.(21),we know that the hopping probability is proportional to Δ2.Such that in the weak electronic coupling limit, the probability for propagation on the acceptor surface is small, and the majority of the trajectories propagates on the donor surface before k(t)reaches the plateau.In such cases,the effect of surface hopping on the trajectory averaging can be neglected, and the SH rate constant is the same as the Ehrenfest result,

1.3 The MQCL method

In the mixed quantum-classical Liouville equation method, dynamics of the Wigner transform of the quantum density matrix isfirst obtained usingthe quantum-classicalapproximation[17-18,21-22]. For the SB model,the MQCL equations can be obtained as

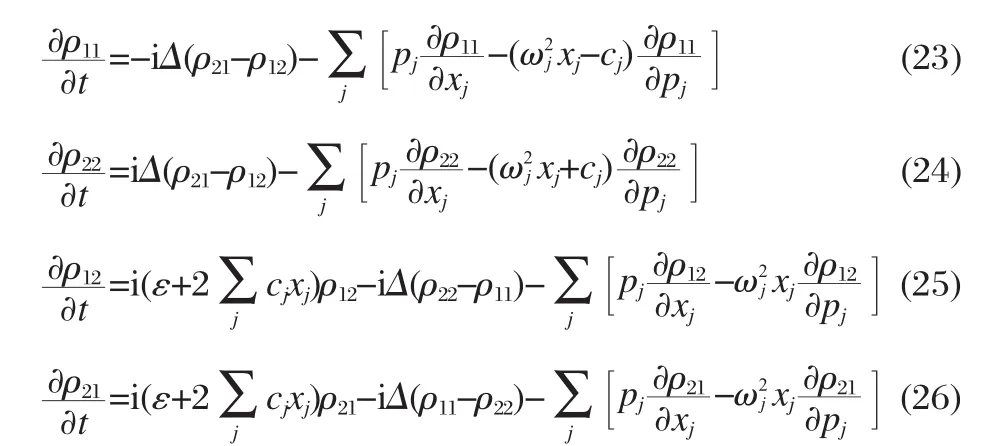
Intheaboveequations,the densitydistribution ρab(x,p)isthe multidimensional Wigner transform of the total density operator ρ:

where a,b=1,2,denote the electronic states and x=(x1,x2,…)Tand Δx=(Δx1,Δx2,…)Tare column vectors,respectively.

Eqs.(23-26)are known to be exact for the spin-boson model (e.g.,Refs.[20,37]).However,this set of multi-dimensional coupled partial differential equations is still hard to solve.In the nonadiabatic limit,the MQCL method will give the correct Fermi golden rule(FGR).The following derivation is for the reason of completeness and comparison with the Ehrenfest and SH methods.

We first define

then integrate the phase space variables x and p in Eq.(23),

The perturbation calculation can be performed by setting ρ22and ρ11as their initial values in Eq.(25),ρ12can then be calculated using classical trajectory method,

The initial distribution is taken from Eq.(18),while the dynamics is on the average surface,

Assuming that P1(t)≈1 when the plateau is reached,by combining Eqs.(29)and(30)

This is the FGR result.

2 Results and discussion

The Ehrenfest and SH rates(Eq.(19)and Eq.(22))only have subtle difference with the FGR rate(Eq.(32)):in calculating the oscillatory part of the integrand,the sinωjt term in Eq.(32)is replaced by the ωjt term.This will not cause a problem when only low frequency modes are involved,or when the exponential part decays very quickly.As in such cases,it becomes safe to replace sinωjt with ωjt,and the two rate expressions are equivalent. However,this is not the case when high frequency modes are involved,and we will present two such examples in calculating charge transfer rates in organic semiconductors below.In such systems,high frequency vibrations are ubiquitous and their contributions to the reorganization energy are usually large[28-29,38-39].

We choose rubrene and sexithiophene as two examples to show the problem when high frequency modes are involved. Molecular structure of the two systems,as well as the methods to obtain the parameters used in the SB model are described in Ref.[40-41].The hole self-exchange reactions were considered in this paper,such that ε=0.The weak electronic coupling approximation is valid for the charge transfer in the c direction of rubrene(Δ=12.1 cm-1)and sexithiophene(Δ=5.8 cm-1)[40-41].

In the hole self-exchange reactions considered for a molecular dimer,the two electronic states are｜M+1M2〉and｜M1M+2〉,where the positive charge resides on monomers 1 and 2,respectively. The harmonic boson modes that couple to the electronic DoFs consist of normal modes from both the neutral and cationic molecules.The contributions to the reorganization energy from each intramolecular mode of both the neutral and cationic molecules are shown in Fig.1.Using these parameters,the charge transfer rates were obtained from Eqs.(19),(22),and(32) and are shown in Fig.2.We can see that the difference between the Ehrenfest and SH methods and the FGR is significant.For rubrene,the rates from the Ehrenfest and SH methods are found to be larger than the result of FGR in very low temperatures and become substantially lower than the result of FGR when the temperature is higher than 20 K.For sexithiophene,the rates from the Ehrenfest and SH methods are consistently lower than the FGR result in the investigated temperature region.

The common feature of the two systems is that the high frequency modes contribute significantly to the reorganization energy,which leads to different rates calculated from Eqs.(19),(22), and(32).To see more explicitly that the difference be-tween the Ehrenfest(SH)and FGR rates is mainly due to the high frequencymodes,we calculated the integrands of Eqs.(19),(22),and(32) as a function of time for rubrene,and the results are shown in Fig.3.The inset shows the contributions from the low frequency (ω＜500 cm-1)and high frequency(ω＞500 cm-1)modes to the total integrand.It can be seen that when all modes are considered,the integrands of Eqs.(19)and(22)differ significantly from that of Eq.(32),and the difference is largely caused by the high frequency modes,which eventually leads to the different electron transfer(ET)rates.

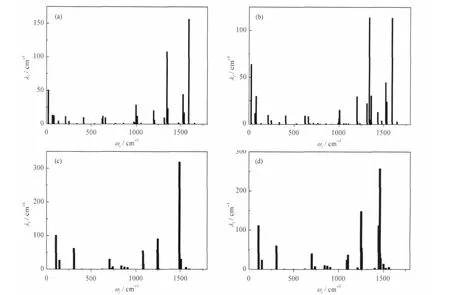
Fig.1 Individual vibrational frequency ωjfor rubrene and sexithiophene,and their contributions to the total reorganization energy λj(a)neutral rubrene,(b)cationic rubrene,(c)neutral sexithiophene,(d)cationic sexithiophene; The total reorganization energies for rubrene and sexithiophene are 1212.3 and 2061.0 cm-1,respectively.

Fig.2 Charge transfer rates as a function of temperature in nonadiabatic limit(a)rubrene,(b)sexithiophene;solid line:Fermi golden rule result, dashed line:Ehrenfest method or SH method;k0=Δ2/λ

Fig.3 The integrand of Eqs.(19),(22),(32)at 300 K as functions of time for rubrene with all the modes shown in Fig.1The inset shows the results with the modes whose frequencies are(a)below 500 cm-1and(b)above 500 cm-1.solid line:Fermi golden rule result, dashed line:Ehrenfest or SH result

As the MQCL method is exact in the nonadiabatic limit in the spin-boson model considered here,comparison of the three mixed quantum-classical methods reveals the problem of the Ehrenfest and SH methods found in the examples presented in this section:the critical problem is the treatment of the dynamics of the coherence terms(Sxand Syin the Ehrenfest and SH methods,and ρ12in the MQCL method).As shown in the MQCL method,dynamics of this term should be calculated on the average potential surface for the SB model.However,the Ehrenfest method describes it on the ensemble averaged potential,and SH method calculates its propagation by hopping between two surfaces.In the special case considered in this paper(weak electronic coupling,initial nuclear distribution equilibrated on the donor surface),both methods are applied to calculate the dynamics of the coherence term on the donor surface,which leads to the different rate constant expressions from the MQCL method.The above findings indicate that the Ehrenfest and SH methods should be used with caution when high frequency motions are important in the system-bath coupling.

3 Conclusions

In this paper,we have derived the charge transfer rate constants from the Ehrenfest,SH,and MQCL methods in the nonadiabatic limit.The results are applied to calculate charge transfer rates in organic semiconductor materials.It is found that the rate constants from Ehrenfest and SH methods can differ significantly from the correct result.Analysis shows that the dynamics of the off-diagonal terms of the density matrix are not correctly described in both methods,and the deviation is more severe when high frequency modes are involved.

1 Makri,N.J.Math.Phys.,1995,36:2430

2 Makri,N.Ann.Rev.Phys.Chem.,1999,50:167

3 Beck,M.H.;Jackle,A.;Worth,G.A.;Meyer,H.D.Phys.Rep., 2000,324:1

4 Thoss,M.;Wang,H.B.;Miller,W.H.J.Chem.Phys.,2001,115: 2991

5 Wang,H.;Thoss,M.J.Chem.Phys.,2003,119:1289

6 Micha,D.A.J.Chem.Phys.,1983,78:7138

7 Billing,G.D.J.Chem.Phys.,1993,99:5849

8 Stock,G.J.Chem.Phys.,1995,103:1561

9 Tully,J.C.;Pretson,R.K.J.Chem.Phys.,1971,55:562

10 Tully,J.C.J.Chem.Phys.,1990,93:1061

11 Webster,F.J.;Wang,E.T.;Rossky,P.J.;Friesner,R.A.J.Chem. Phys.,1994,100:4835

12 Coker,D.F.;Xiao,L.J.Chem.Phys.,1995,102:496.

13 Prezhdo,O.V.;Kisil,V.V.Phys.Rev.A,1997,56:162

14 Müller,U.;Stock,G.J.Chem.Phys.,1997,107:6230

15 Fang,J.Y.;Hammes-Schiffer,S.J.Phys.Chem.A,1999,103: 9399

16 Tully,J.C.Faraday Discuss.,1998,110:407

17 Martens,C.C.;Fang,J.Y.J.Chem.Phys.,1997,106:4918

18 Kapral,R.;Ciccotti,G.J.Chem.Phys.,1999,110:8919

19 Santer,M.;Manthe,U.;Stock,G.J.Chem.Phys.,2001,114:2001

20 Mac Kernan,D.;Ciccotti,G.;Kapral,R.J.Chem.Phys.,2002, 116:2346

21 Shi,Q.;Geva,E.J.Chem.Phys.,2004,121:3393

22 Kapral,R.Annu.Rev.Phys.Chem.,2006,57:129

23 Bader,J.S.;Berne,B.J.J.Chem.Phys.,1994,100:8359

24 Egorov,S.A.;Rabani,E.;Berne,B.J.J.Phys.Chem.B,1999, 103:10978

25 Egorov,S.A.;Rabani,E.;Berne,B.J.J.Chem.Phys.,1999,110: 5238

26 Egorov,S.A.;Rabani,E.;Berne,B.J.J.Chem.Phys.,1998,108: 1407

27 Rabani,E.;Egorov,S.A.;Berne,B.J.J.Chem.Phys.,1998,109: 6376

28 Brédas,J.L.;Beljonne,D.;Coropceanu,V.;Cornil,J.Chem.Rev., 2004,104:4971

29 Coropceanu,V.;Cornil,J.;da Silva Filho,D.A.;Oliver,Y.;Silbey, R.;Brédas,J.L.Chem.Rev.,2007,107:926

30 Gershenson,M.E.;Podzorov,V.;Morpurgo,A.F.Rev.Mod. Phys.,2006,78:973

31 Leggett,A.J.;Chakravarty,S.;Dorsey,A.T.;Fisher,M.;Garg,A.; Zwerger,W.Rev.Mod.Phys.,1987,59:1

32 Weiss,U.Quantum dissipative systems.2nd ed.London:World Scientific,1999

33 Heller,E.J.J.Chem.Phys.,1976,65:1289

34 Filinov,V.S.;Medevedev,V.V.;Kamskyi,V.L.Mol.Phys., 1995,85:711

35 Sun,X.;Miller,W.H.J.Chem.Phys.,1997,106:916

36 Pollak,E.;Liao,J.L.J.Chem.Phys.,1998,108:2733

37 Frantsuzov,P.A.J.Chem.Phys.,1999,111:2075

38 da Silva Filho,D.A.;Kim,E.G.;Brédas,J.L.Adv.Mater.,2005, 17:1072

39 Yang,X.D.;Wang,L.J.;Wang,C.L.;Long,W.;Shuai,Z.G. Chem.Mater.,2008,20:3205

40 Nan,G.J.;Yang,X.D.;Wang,L.J.;Shuai,Z.G.;Zhao,Y.Phys. Rev.B,2009,79:115203

41 Nan,G.J.;Wang,L.J.;Yang,X.D.;Shuai,Z.G.;Zhao,Y. J.Chem.Phys.,2009,130:024704