聚炔、累积多烯与全碳环分子的模糊对称性

邢生凯 李 云 赵学庄 尚贞锋 许秀芳蔡遵生 王贵昌 李瑞芳

(南开大学化学学院,天津 300071)

Fuzzy symmetry is an interesting topic in theoretical chemistry and a few important results have been obtained[1-11].In our recent papers,some methods have been established to study the fuzzy symmetry of molecule structures and molecular orbitals (MOs)[12-13].Based on these methods,we analyzed the fuzzy symmetry characterization of the static and dynamic molecular systems[14-21].For one-dimensional fuzzy periodicmolecules, we have investigated the π-MO of linear polyyne molecules(e.g., C16H2)and their cyanides and have obtained some very importantresults[17].However,thetediouscalculationsnotonlyintroduced some margin of errors(these errors do not affect the obtained conclusion though),but also restricted doing more calculations. Therefore,we only analysed the MO fuzzy symmetry of the C16H2molecule and its cyanide[17].Thanking for the improvement of our calculation levels recently,we can now study the MO fuzzy symmetry of polyynes with varying numbers of carbon atoms(C-atoms)systemically.As for the straight chain cumulative polyene,although the molecular skeleton is not completely linear,the carbon atoms which form the π-MOs are linear positioned in the polyene molecule and could be treated with fuzzy groupIn polyyne molecules(CnH2),n is always even and the pair of π-MOs formed by p-AO(atomic orbital)in x-and y-directions are one-to-one corresponding,degenerate,and central symmetrical.Generally,it is only necessary to analyze the π-MO in one direction.However,unlike in polyyne,the number (n)of C-atoms in cumulative polyene(CnH4)molecules can be either odd or even[22].Further,the molecule is of a planar structure when n is an even number,and the pair of π-MOs composed of the p-AOs in x-and y-directions are non-degenerate but keeping the central symmetry.When n is odd,the molecule is non-planar and the pair of π-MOs formed by p-AOs in x-and y-directions are degenerate,but losing the central symmetry.We will investigate the fuzzy symmetry for all the different situations mentioned above.On the basis of Born-Karman approximation[23-24], the one-dimensional periodic symmetry group with n units and the Cnpoint group are isomorphic with each other.Thus,the symmetry and fuzzy symmetry features of MOs of the full carbon ring molecules can be and have been also analyzed.There are two kinds of full carbon ring molecules,C≡C—C≡C and C=C=C,and both the experimental and theoretical researches arelimited.Theprevious study[25-26]suggested that:the carbon ring molecules tend to form linear or annular structures when the number of the carbon atoms is less(n≤20),while it is prone to form spatial three-dimensional structures as n further increases. Because when n is 4i+2(i is integer),such as C10,C14,and C18,etc., the molecules are more stable[25-26],the fuzzy symmetry of two full carbon ring molecules,C6and C18,will be investigated in this work.

1 Fuzzy symmetry of polyyne molecules

Since the linear polyyne molecule was reported in 1952[27], therehavebeensome related theoretical researches published[28-30]. We also made some preliminary studies on the one-dimensional fuzzy symmetry of polyyne molecules[17].However,the tedious calculations involved would result in not only a certain errors(or mistakes)but also the limitation for more extensive and pervasive studies on the fuzzy symmetry of such molecules to follow; thereby the π-MOs of only a few typical molecules have been analyzed.Although the relative results we have obtained are creditable,the more general characters of such molecules have not yet been established more extensively.By improving the calculation procedure,we now in this work explore the fuzzy symmetry of the π-MOs in linear polyyne molecules containing different numbers of carbon atoms.

According to the linear combination of atomic orbital(LCAO) π-MO theory,the ρth MO Ψρcan be expressed as:

where φ(J,i)is the ith AO of the Jth atom;aρ(J,i)is the corresponding LC coefficient and usually a real number.For AO,the criterion of φ(J,i),i.e.YJi,is a2ρ(J,i).The corresponding membership function(μY)of the symmetry transformation G can be expressed as[12-17]:

In formula(2),only one AO of each atom participates in the formation of π-MO and thus the summation of J and i can be done by choosing running through any one of them.Here,G is the symmetry transformation that translates several integral space periodic length(two carbon atoms are included in each space periodic length or each one-dimensional unit cell).G and M refer to atom and molecule,respectively.

All the calculations for MO are performed by Gaussian 03 program at the HF/STO-3G level[31].There are 4n π-MOs in the polyyne(C2nH2)formed by even number(2n)of C-atoms,and these π-MOs are double degenerate and distributed in 2n different energy levels.Among the n energy levels there are 2n occupied bonding π-MOs,and among the n levels remained there are 2n empty anti-bonding π-MOs.Both the highest occupied molecular orbital(HOMO)and the lowest unoccupied molecular orbital (LUMO)are double degenerate and defined as π-OMO-1(occupied molecular orbital)and π-VMO-1(vacant molecular orbital), respectively.The other bonding and anti-bonding π-MOs are denoted as π-OMO-j and π-VMO-j,respectively.Here j is the serial number of the energy level where the MO belongs,it is 1 for the frontier MO,and is j-1 away from the frontier MO according to the energy level.Of course,π-OMO-j and π-VMO-j are double degenerate.Usually only one of the double degenerate π-MOs needs to be discussed.Now,we calculate the polyynes with less than 40 C-atoms at the level of HF/STO-3G,then calculate the membership function of different π-MOs correspondingtothesymmetrytransformationoftranslating lperiodiclength (i.e.,2l carbon-carbon atom distance),T(l),according to the formula(2).For C40H2,the calculated results of π-MO near the frontier energy level are displayed in Fig.1.

Interestingly,the result in Fig.1 is almost in consistent with that of C16H2[17].In fact,we can get the same result for the linear polyynes containing more carbon atoms.In order to explore the regularity,the membership functions corresponding to the parallel translation symmetry transformation of polyyne with different numbers of C-atoms are investigated.As shown in Fig.2,we display the membership functions of the parallel translation T(l) thattranslatingone,two,andthreeperiodiclengths(l=1,2,3;each period length containing two C-atoms)of each π-MO in four polyyne molecules.

Fig.1 Membership functions of the π-MOs near the frontier energy level corresponding to the symmetry transformation of translating l periodic length(2l carbon-carbon atom distance)for C40H2molecule

In Fig.2,since the numbers of C-atoms are different in the four polyyne molecules,the numbers of π-MOs and the curves of membership function vs π-MO are also different.However, the shapes of these curves are similar to a certain degree,especially for the polyynes comprised of much more C-atoms.If we investigate enough polyyne molecules(C2nH2)and use the value of j/n to replace the j in Fig.2,the results in Fig.3(A-C)can be obtained.The membership functions corresponding to T(l)transformation distribute symmetrically in both sides of the nonbonding energy level(j/n=0.0;j=0.0),and approximately form l branches of the U-shaped curves at each side.At both ends(j/n= 1.0;j/n=-1.0)of the diagrams,the corresponding membership function data appear a vertical distribution like a potential well. Fig.3(A-C)depicts the membership functions when the value of l equals to 1,2,and 3,respectively,but we also explore larger l value in the T(l)transformation and get the similar results except that the dispersion of data is getting obvious with the increasing of l.The results discussed above are similar to those for some space group symmetry transformation of linear conjugate polyenes based on the AM1 calculations[20].Impressively,Fig.3 (D)displays distribution of the energy of π-MO vs(j/n).If we regard all such polyyne molecules as one-dimensional crystal, the energy level distribution curve branches of OMO and VMO asymp-totically represent the corresponding“fuzzy”filled and conduction bands for this crystal comprised by all of the polymer molecules,and the interval between these two energy curve branches is the forbidden band.Thus,the energy gap can be easily obtained from this plot.

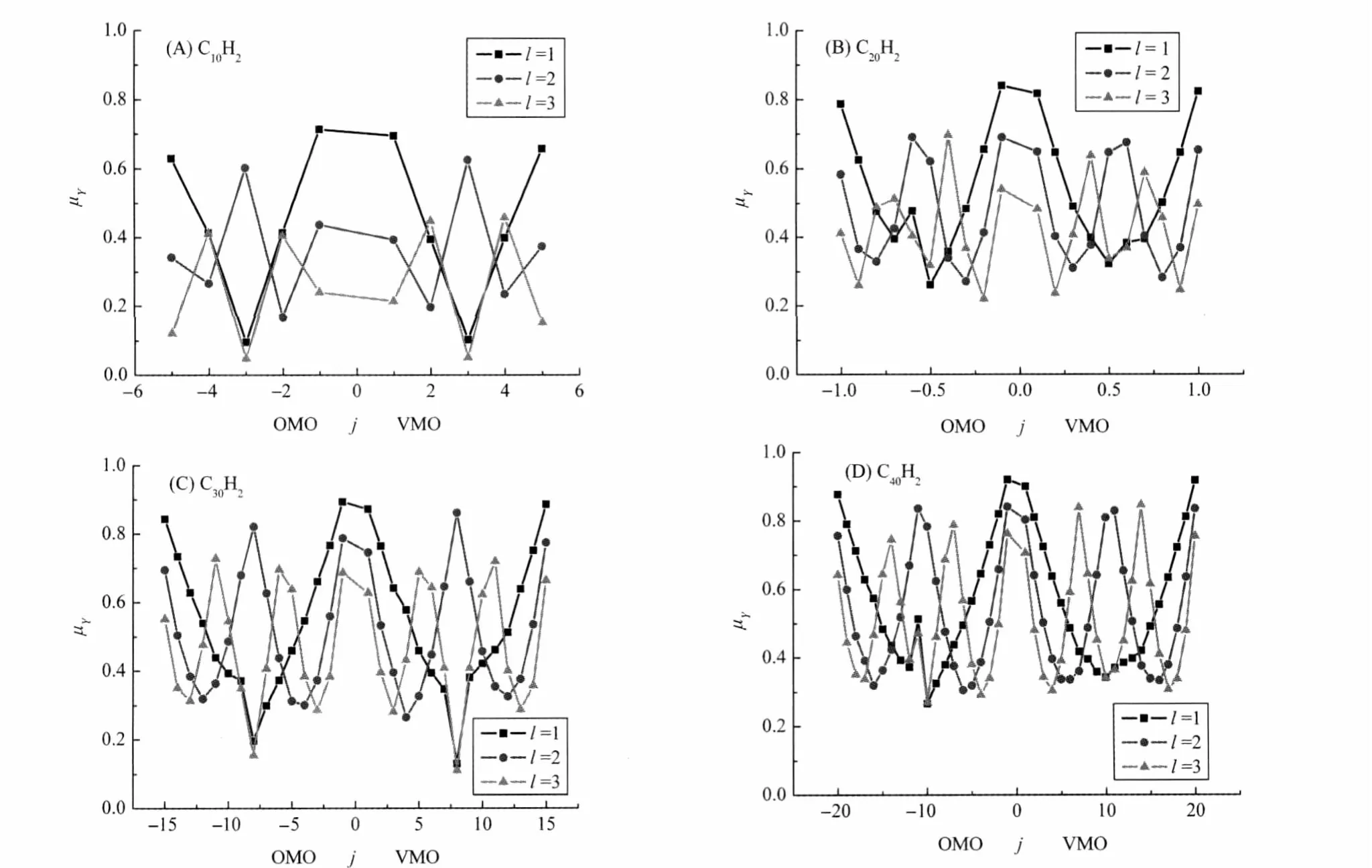
Fig.2 Membership functions of each π-MO in four polyyne molecules related to the translation symmetry transformation T(l) about translating one,two,and three periodic length calculated at the HF/STO-3G level

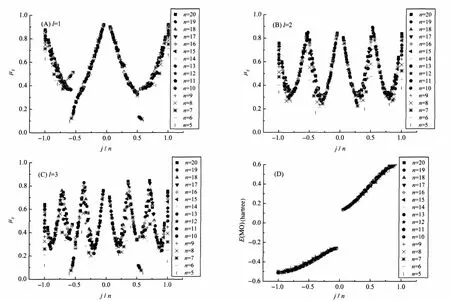
Fig.3 Characteristic curves of the membership functions of the π-MOs of polyyne molecules related to the translation symmetry transformation T(l)(l=1,2,3)vs j/n(A,B,C)and the π-MO energy vs j/n(D)

These polyyne molecules have usually the symmetry center and the membership functions of their π-MO about the center inverse transformation are all one.The corresponding irreducible representations are pure:either pure symmetric(g)or pure antisymmetric(u).

2 Fuzzy symmetry of cumulative polyene molecules

Polyene molecules can be divided into discrete polyene,conjugate polyene,and cumulative polyene molecules according to the relative positions of the double-bonds in the molecules.Similar to the polyyne,the C-atoms in the cumulative polyene connected by double-bond are linear,and the molecule formula of cumulative polyene is CmH4.Different from polyyne,the number of C-atoms,m,can be either even(m=2n)or odd(m=2n-1).When m is an even,the four H-atoms are coplanar with the carboncarbon chain of polyene molecule and the molecule belongs to the point group D2h.When m is an odd,the four H-atoms are not coplanar with the carbon chain and the molecule belongs to the point group D2d[22].In the cumulative polyene,two perpendicular p-AOs of each C-atom participate in forming the π-MO(for the terminal C-atoms,only one p-AO participates).Because the difference of odevity of the C-atoms results in the difference of symmetry point group,the corresponding fuzzy symmetry will be analyzed.

2.1 Fuzzy symmetry of C2nH4

For cumulative polyene formed by m(m=2n)C-atoms,the 2n p-AOs are perpendicular to the molecular plane to form 2n π-MOs,n bonding OMOs and n anti-bonding VMOs.Among the other 2n p-AOs which are coplanar with the molecular plane, the p-AOs of the terminal C-atoms form π-MO with the s-AO of the four H-atoms while the other 2(n-1)p-AOs form 2(n-1)π-MOs,including(n-1)bonding OMOs and(n-1)anti-bonding VMOs.Because the π-MOs only tiny overlap with the π-MOs, they can be omitted in the following analysis.In this paper,we only investigate the 2n π-MOs perpendicular to the molecular plane and the other 2(n-1)π-MOs coplanar with the molecular plane.All of these π-MOs have the central symmetry with the pure irreducible representation,symmetric(g)or anti-symmetric (u).Differentfromthepolyyne,the π-MOsof cumulative polyene are non-degenerate.And the methods employed in analyzing the π-MOs of polyyne can also be used to investigate those in the cumulative polyene.Similar to Fig.3,we display the membership functions of these two kinds of π-MOs,related to the parallel translation symmetry transformation(l=1,2,3)of the cumulative polyene molecules with different even carbon atoms,in Fig.4(A-C)and Fig.5(A-C),respectively.It should be noted that the periodic length(the length of the one-dimensional unit cell) contains two C-atoms because the neighboring double-bonds should be considered to have different orientations.Since in any specified polyene molecule,the numbers of those two kinds of π-MOs are different,the abscissas of Fig.4 and Fig.5 are labeled by different units,but their denominators always denote the number of the relevant π-OMO or π-VMO.Interestingly,although the numbers of two kinds of non-degenerate π-MOs are different,the distributions of the relevant membership functions and the energies of the MOs are similar as indicated by Figs.4 and 5.Moreover,the distribution characteristics are also similar to those of the π-MOs of polyyne(Fig.3),not only qualitatively in the shape of distribution,but also quantitatively in the magnitude of the membership functions.This may reflect some common features of this kind of π-MOs.

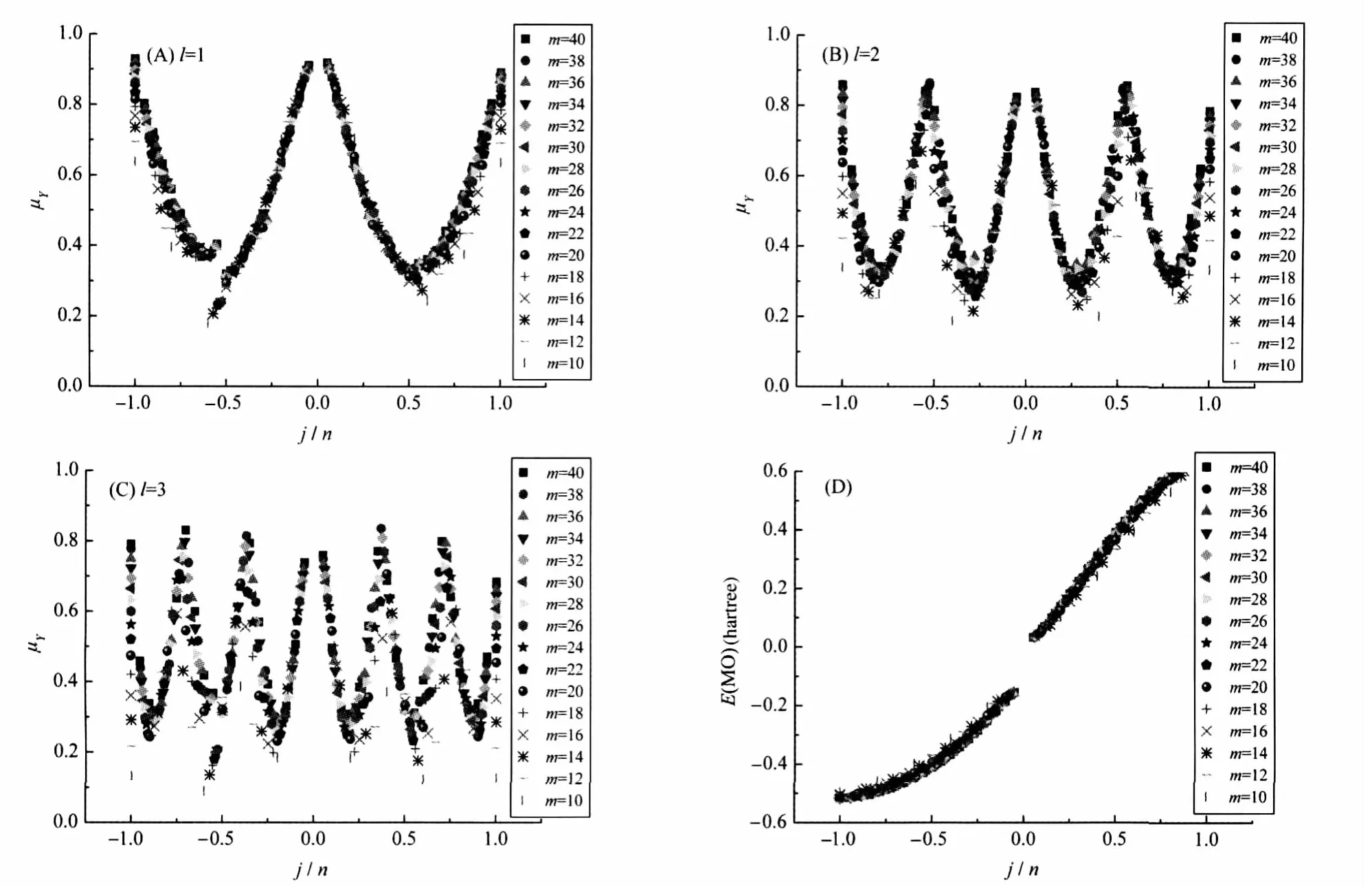
Fig.4 Characteristic curves of the membership functions of π-MOs perpendicular to the molecular plane about the translation symmetry transformation T(l)(l=1,2,3)vs j/n(A-C)and the MO energy vs j/n(D)in the CmH4(m=2n)molecules

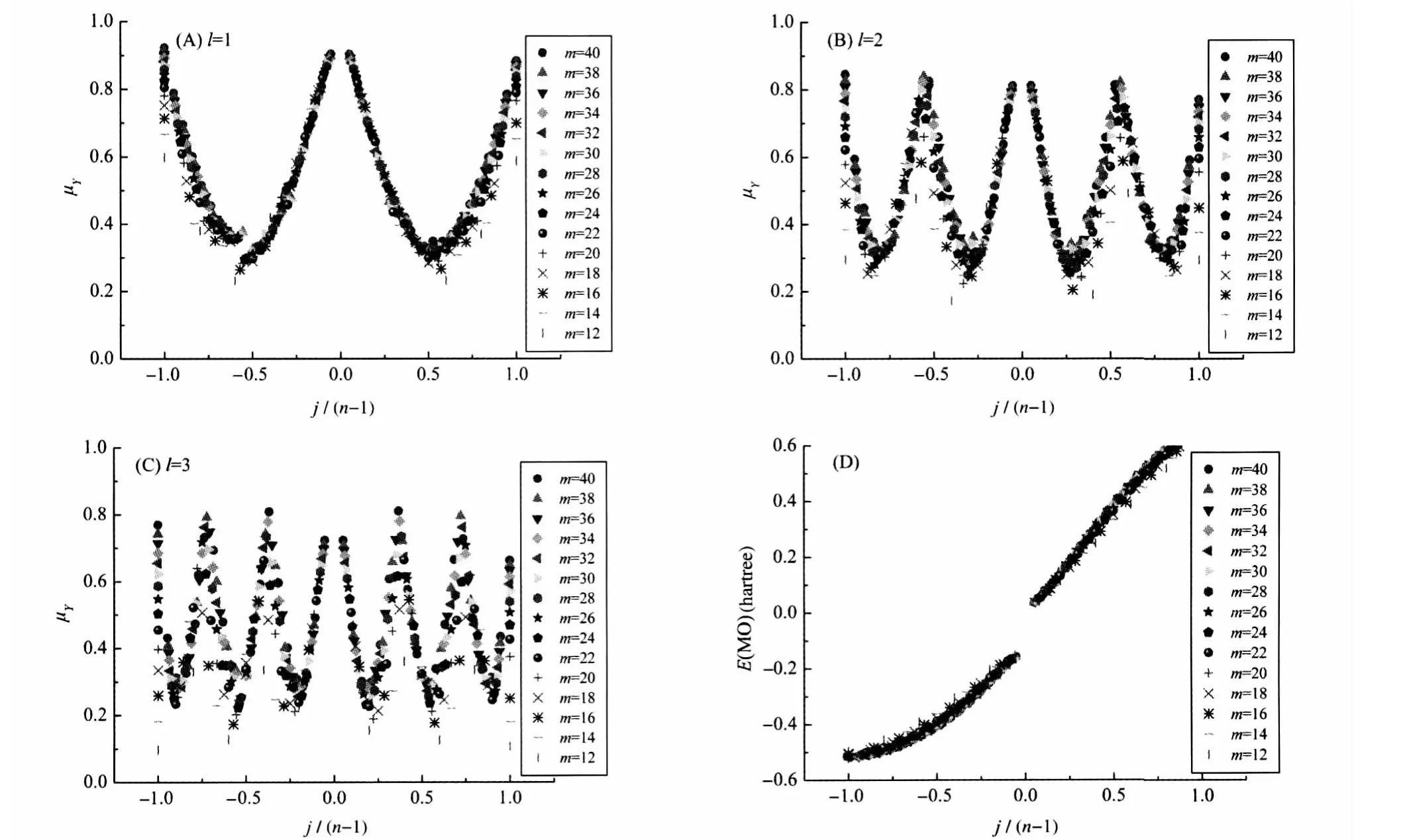
Fig.5 Characteristic curves of the membership functions of π-MOs in the molecular plane about the translation symmetry transformation T(l)(l=1,2,3)vs j/(n-1)(A-C)and the MO energy vs j/(n-1)(D)in the CmH4(m=2n)molecules

2.2 Fuzzy symmetry of C2n-1H4

For cumulative polyene with odd C-atoms(m=2n-1),the two terminal CH2groups of the molecule locate in two perpendicular planes,so that the whole molecule has the symmetry of point group D2d.The simplest cumulative polyene is allene and its fuzzy symmetry characteristics in the internal rotation process have been probed into[19,21].In C2n-1H4molecules,the p-AOs distribute into two perpendicular planes,and the planes intersect at a carbon-carbon chain comprised of(2n-1)C-atoms.In each plane, the p-AOs not only form two π-MOs with two H-atoms,but also form(2n-2)π-MOsincluding(n-1)π-OMOsand(n-1)π-VMOs. Though the linear carbon chain containing(2n-1)C-atoms has central inverse symmetry,the whole polyene molecule and its π-MOs do not have the well-defined central inverse symmetry,and we call that they only have the corresponding fuzzy symmetry. Because the π-MOs in the two planes are degenerate,only one case needs to be explored.Their membership functions of periodic parallel translation symmetry transformation are investigated by the method analogous to the one used previously,and the results are shown in Fig.6.Due to the imperfectness or fuzziness/roughness of the central inverse symmetry of these MOs, their relevant membership functions are not always 1 and the value can be obtained by formula(2),where G is the central inverse symmetry transformation(i.e.,parity transformation).The membership functions of each π-MO for the cumulative polyene molecules with different odd C-atoms are shown in Fig.7(A), which is somewhat similar to that of the translation symmetry transformation translating one period,but the difference in the curve shape between the two cases is very obvious.

Due to the imperfectness of the central inverse symmetry of the π-MO in C2n-1H4molecules,the relevant membership functions are not always one.As shown in Fig.7(A),the points do not all fall on the horizontal line,in which the value of the membership function is always 1.Their corresponding irreducible representations are not pure,and they are the superposition of the symmetrical and the anti-symmetrical representation[13-14].The LCAO coefficients can be decomposed into symmetrical and anti-symmetricalcomponentsrelatedtothe π-MOinformula(1):

Fig.6 Characteristic curves of the membership functions of π-MOs of many CmH4(m=2n-1)molecules about the parallel translation symmetry transformation T(l)(l=1,2,3)vs j/(n-1)(A-C)and the MO energy vs j/(n-1)(D)

Fig.7 Characteristic curve of the membership functions of π-MOs of many CmH4(m=2n-1)molecules about the central inverse symmetry transformation(P)(A)and component of the irreducible representations X(P)(B,C,D)

Here,the serial number i of AO can be and has been omitted because only one AO from each atom participants in the formation of LCAO of MO.The LCAO coefficients are all normalized within the system.Under the central inverse symmetry transformation P(G=P),the corresponding LCAO coefficient is:

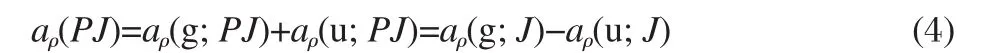
Thus,aρ(g;J)and aρ(u;J,i)can be obtained by aρ(J,i)and aρ(GJ,i),respectively.Easy to prove that:

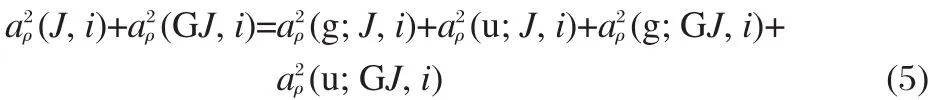
The symmetrical and anti-symmetrical representation components of the MO are denoted in formulas(6a)and(6b),respectively:

Taking C39H4as an example,the symmetrical and anti-symmetrical representation components of each π-MO are shown in Fig.7 (B).The relevant points distribute in an X-shaped cross pattern. The similar results can be obtained from cumulative polyene molecules containing different odd C-atoms as shown in Fig.7 (C).The X-shaped pattern displays noticeable dispersion of the irreducible representation components,but the dispersion will be reduced greatly when plotted by replacing j with j/(n-1)(Fig.7 (D)).

3 Symmetry and fuzzy symmetry of full carbon ring molecules

On the basis of Born-Karman approximation[23-24],one-dimensional periodic symmetry group comprised of n units is isomorphic with point group Cn.The fuzzy symmetries of full carbon ring molecules with point group Cnsymmetry are investigated in order to compare with linear carbon chain.Experimental and theoretical research on this kind of molecules are very limited and the previous study[25-26]has suggested that the number of their C-atoms is usually even,and they tend to form carbon ring structure when the number of C-atoms is less than twenty(n≤20),but they are prone to form spatial three-dimensional structure as n further increases.The molecules are more stable when the number of C-atoms is equal to 4i+2(such as C10,C14,and C18)[25-26].It is difficult to distinguish the two kinds of connection types between carbon atoms(i.e.,C≡C—C≡C or C=C=C=C),however,for C4i+2molecules,it maybe more appropriate to study the symmetry character for the C=C=C=C type.Full carbon ring can also be regarded as annular and cumulative polyene.

In full carbon ring molecule,the p-AOs of C-atoms can take either one of the two orthogonal orientations.One is perpendicular to the molecular plane,and the other one is also in a plane but perpendicular to the carbon-carbon ring.However,the coor-dinates in Gaussian program is Cartesian coordinates,in which the Z direction is perpendicular to the molecular plane and the X, Y directions are perpendicular to each other in the molecular plane.The direction of pz-AOs of the full carbon ring molecule coincides with that of the Z-axis,and those of the other two p-AOs(denoted by pr-AO and pt-AO,they are perpendicular to each other)vary with the changes of the C-atoms.Therefore,the orientation of p-AOs in the molecular plane should first be determined,then the full carbon ring as shown in Fig.8 is investigated.In Fig.8,only part of the carbons is shown and the center(O) of carbon ring is the origin of the Cartesian coordinate system.It is always possible,for only one C-atom,the directions of px-AO and py-AO are set in consistent with those of the corresponding Cartesian coordinate system provided by the Gaussian program, but for the rest of the C-atoms the directions of pr-AO and pt-AO have to vary with the specified C-atom.

Thus,the linear combination of s-,px-,and py-AO of the MO need to be transformed into the combination of s-,pr-,and pt-AO, and the standard Cartesian coordinates provided by Gaussian program have to be converted into the cylindrical coordinates. Namely,the standard Cartesian coordinates of the molecular plane are converted into the polar coordinates.As shown in Fig. 8,the plane Cartesian coordinates X and Y are converted to polar coordinates r and θ,where r is the displacement from origin(O) to the corresponding carbon atom and θ is the angle between vector r and axis OX.Apparently,θ is also the angle between pr-AO and px-AO.Thereby,the standard Cartesian coordinate values for each carbon atom position obtained from the Gaussian program can be converted into cylindrical coordinate values. Furthermore,according to the rule of coordinate frame rotation, the LCAO coefficients of MO of px-AO and py-AO can be converted to that those of pr-AO and pt-AO.While the LCAO coefficients of s-AO and pz-AO need not to be converted.

For full carbon ring molecule Cm,if only the AOs of carbon shell are considered to form MOs,the symmetry adapted linear combination of atomic orbital(SALC-AO)can be divided into four sets:

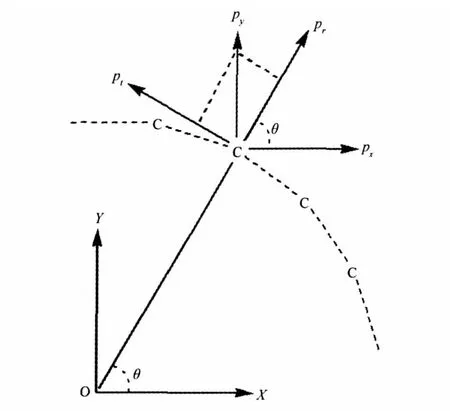
Fig.8 Directions of the p-AOs located in the molecular plane for full carbon ring molecule

The irreducible representation related to each SALC-AO set is identical when treated according to point group Cm.If treated according to point group Dmh,the first two sets G(s)and G(pr)will remain the same,while the one-dimensional irreducible representation of G(pt)is different from the first two sets although its two-dimensional irreducible representations may be the same. However,the one-,two-dimensional irreducible representations of G(pz)are all different from G(s)and G(pr).The SALC-AO belonging to the same irreducible representation but different groups can be superposed by LCAO to form MO,while the π-MO comprised of 2pz-AO of G(pz)can be analyzed separately and is independent of AO of other sets.On the contrary,the π-MO formed by the 2pr-AO of G(pr)usually superimpose with AO of other sets belonging to the same irreducible representation. Certainly,the fact that sometimes more than one set need to be considered must cause the relevant symmetry and fuzzy symmetry analysis becoming a rather complicated issue(especially for smaller full carbon ring molecules,the situation is more serious). In addition,the pair of pr-AOs at the opposite positions may also perform non-π-type combination.So,two specific full carbon ring molecules are analyzed in detail.It should be noted that the one-dimensional periodic symmetry group of m units is isomorphic with the point group Cm(not the point group Dmh)according to the Born-Karman approximation.And thereby,sometimes the analysis of full carbon ring will be considered based on the point group Cm.

3.1 Symmetry and fuzzy symmetry of C6-ring molecule

The LCAO of the valence-shell of C6-ring molecule can form 24 MOs,in which the bonding OMO and anti-bonding VMO are both 12.According to the point group D6h,the 6 MOs formed by 6 pz-AOs can be divided into two one-dimensional irreducible representations(A2u,B2g)and two two-dimensional irreducible representations(E1g,E2u).They can be expressed as follows:

Here,(8a-8c)are bonding OMOs and(8d-8f)are VMOs,and the situation agrees with the 6 π-MOs of benzene molecule,but of course,the coefficients αj(j=1,2,…,6)are altered.By the way, for the π-MOs of benzene calculated at different levels,the formulas(8a-8f)are tenable but the coefficients αj(j=1,2,…,6)do not remain the same[16].This is also tenable for C6-ring molecule. Anyway,the MO of the one-dimensional irreducible representation should be the eigenstate of all the symmetry transforma-tions of the relevant point group and the corresponding membership function should be 1.But the single MO of the two-dimensional irreducible representation is not the eigenstate of all the symmetry transformations of the relevant point group and some of their membership function will be less than one,so we can only analyze their fuzzy and imperfect symmetry.For example, for the MO in(8b-8e),the rotation symmetry transformations of 60°and 120°,C6and(C6)2,are investigated individually,their membership functions are both 0.5,which are consistent with the corresponding π-MO of benzene molecule.For the other MO,the situation is very complex because of containing different SALC-AO sets(7a-7c).Based on the point group D6h,the irreducible representation of set G(pz)is:

The corresponding irreducible representations of G(s)and G(pr) are the same and expressed as follows:

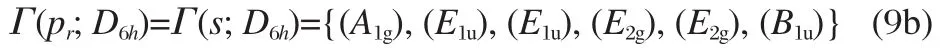
The corresponding irreducible representation of group G(pt)is:

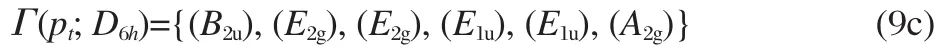
According to the point group C6,the irreducible representations of all these SALC-AO sets are the same:

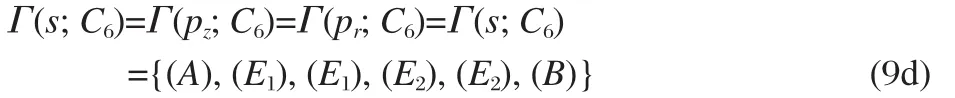
For C6-ring molecule,the MOs that belong to one-dimensional irreducible representation but contain different sets of SALCAO are still the eigenstate of the symmetry transformation of the relevant point group and the membership function is 1.For the MOs belonging to two-dimensional irreducible representation, their membership functions of some symmetry transformation are less than one whether they contain different sets of SALCAO.The membership functions are 0.5 for the symmetry transformation of rotating 60°and 120°,which means that we need only consider the point group C6.However,the molecule itself has the point group D6h,therefore in the light of point group D6h, the irreducible representation of set G(pz)is different from those of the other sets.Frankly,the MO formed by pz-AO does not include the components of other SALC-AO sets,while the MO composed of other SALC-AO sets may contain the components of different sets from each other.

3.2 SymmetryandfuzzysymmetryofC18-ringmolecule

It should be noted that the superposition of different SALCAO sets affects the MO substantially.Sometimes,it is difficult to determine the π-type-MO combined mainly by the set G(pr). So,the normalization criteria of AO which is introduced in researching the fuzzy symmetry is in addition utilized to analyze the impact of different SALC-AO sets on the MO.And,the summation of normalization criteria of AO belonging to the same SALC-AO set is used to represent the set′s contribution to this MO,so that it can also be called the component of SALCAO set in this MO.For MO formed by AO in only one SALCAO set,the component of the SALC-AO set is of course one. For smaller full carbon ring molecule,there are a considerable number of MOs which contain the components from multiple sets of SALC-AO.For example:there are 24 MOs in the valence shell of C6molecule and the rations of their different SALC-AO components are shown in Fig.9(A).According to the point group D6h,the irreducible representation(formula(9a))corresponding to G(pz)is unique from those of the other SALC-AO sets.So,in the 6 π-MOs comprised of G(pz),the components of this SALCAO set are all 1,as shown in Fig.9(A).In addition,the components of G(pt)are all one for two MOs which are the one-dimensional irreducible representations belonging to B2uand A2gof in formula(9c).However,theotherMOscontainmorethanonekind of component from the SALC-AO sets.Especially the component of G(pr)will coexist with other components from other SALC-AO sets,so that it is difficult to analyze the composition of the π-MO.The situation will be improved for the larger full carbon ring molecules.As shown in Fig.9(B),among the different components of the 72 MOs in the valence shell of the C18-ring molecule about the different SALC-AO sets,besides the 18 π-MOs,of which the components of G(pz)are all one,there are quite a few OMOs near the frontier orbital whose components of G(pr)are all close to one.It can be expected that the situation will be further improved in even larger full carbon ring molecules. However,there is a paradox,in general,it is difficult for the larger full carbon ring molecules to maintain the planar structure.

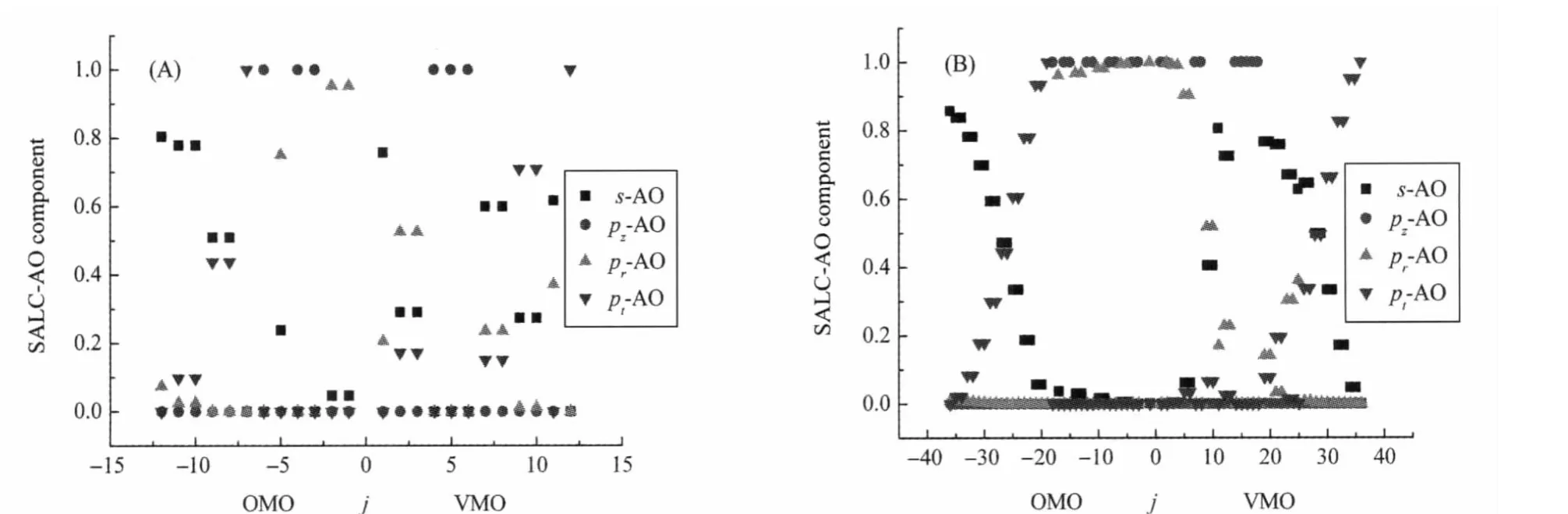
Fig.9 SALC-AO components of MO in the C6(A)and C18(B)molecules

The planar C18-ring molecule has the point group D18hsym-metry with 72 MOs in the valence shell.There are four SALCAO sets(s-,pz-,pr-,pt-AO sets)and each set contains 18 SALCAOs.The symmetry transformation corresponding to the 18 fold axis is the angle rotation with 20°for each fold of operation.For the 18 MOs comprised from G(pz),the membership functions related to the transformation of rotating 20°,40°,60°,and 80°are shown in Fig.10.Of course,the membership functions of the symmetry transformations of rotating±θ and 180°±θ are the same, and the membership functions are all 1 for the transformations of rotating 0°and 180°.In Fig.10,the MOs(j=±9)which the are farthest away from the frontier MO belong to the one-dimensional irreducible representation,and the membership functions are all 1.The other MOs belong to the two-dimensional irreducible representation.Corresponding to the different twodimensional irreducible representations,their membership functions are varied but may less than one.Different from full carbon ring C6-ring molecule,in C18-ring molecule,the corresponding membershipfunctionsmaybevariedfortheMOswhichbelongto different two-dimensional irreducible representation.Of course, there may be some of the MOs belonging to different two-dimensional irreducible representations which have identical membership functions.Some membership functions of these two-dimensional irreducible representations of the point group D18hwhich correspond to the same one-dimensional complex number representation and its conjugate complex number representation of the point group C18are the same.Therefore,only several values of the relevant membership function are displayed in Fig.10.On the other hand,since the C18molecule can form MO containing component of different SALC-AO sets,the irreducible representation of MO combined in that way may rely on the involved SALC-AO sets in relation to the point group D18h.However,the membership functions of these MOs about the rotation symmetry transformation will only depend on the irreducible representation of point group C18.Although the membership functions of these MOs can also obtain the similar result as those in the Fig. 10,the sequence of the energy levels as well as the irreducible representations of the MOs comprising of different SALC-AO components may all be different.

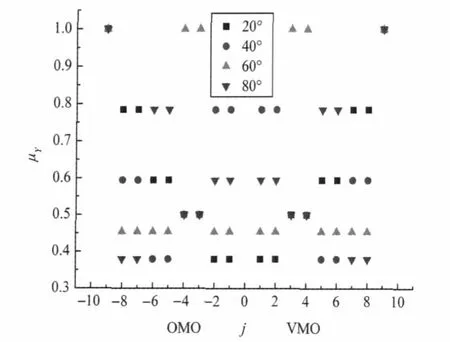
Fig.10 Membership functions of π-MOs comprised of G(pz) about rotation symmetry transformation in the valence-shell of C18molecule

Though there is some comparability between the linear carboncarbon chain and the annular carbon-carbon chain based on the Born-Karman approximation,this approximation is right only when the number of C-atoms is very large.If the C-atoms number is not large enough,we should pay attention to the different characters among these C-atoms when discussing the relevant properties like the fuzzy symmetry and so on.For example,the symmetry center(or the fuzzy symmetry center)of linear carboncarbon chain is on the chain.For annular carbon-carbon chain, the symmetry center is not on the chain but at the center of the whole molecule ring.For linear carbon chain,its two groups of π-MOs in the Cartesian coordinates are perpendicular to each other and in many cases they are degenerate,and for these degenerate π-MOs they will have the same membership functions as well as the same energies.However,when discussed in the cylindrical coordinates,the annular carbon-carbon chain contains two orthogonal sets of π-MOs:one is perpendicular to the molecular plane and comprised of SALC-pzAO,and the other one is in the molecular plane and mainly formed by the SALC-prAO and also contains some component of σ-AO.The two groups of π-MOs are non-degenerate,but it may be degenerate when they come from the same set.In addition,for the MOs belong to the same irreducible representation,they have the same membership functions.

There are not many planar full carbon ring molecules(here, taking C6and C18molecules as examples),but the research methods used in the kind of molecules in this work can actually be applied to explore much more complicated systems.This will be referred in our investigation of the fuzzy symmetry of carbon nanotubes.

4 Conclusions

Based on our previous research on the way in developing the molecular fuzzy symmetry,we investigate the fuzzy symmetry characters of π-MOs of linear and annular molecules formed all by C-atoms.These molecules include polyyne,cumulative polyene,and full carbon ring molecule.The main conclusions obtained are summarized as follows.

(1)Extended the research into the space group fuzzy symmetry for polyyne and investigated the fuzzy symmetry of the π-MO of polyyne molecules comprised of varied numbers of C-atoms about the space translation symmetry transformation systematically.Because the π-MOs of polyyne molecules are all double-degenerate,only one class of them is necessary to be explored.The membership functions of π-MOs of different polyyne molecules about the translation symmetry transformation(l space period length)can be described by a unique distribution characteristic curve approximately.The membership functions of π-MOs of different polyyne molecules are located in the vicinity of the unique distribution characteristic curve. This characteristic curve is approximate symmetry about the non-bond energy level.The bonding π-MO and anti-bonding π-MO can respectively form l opening upwards branches,which is somewhat similar to some results of conjugate polyene.

(2)We can produce the π-MO energy distribution characteristic curve of polyyne molecules using the similar method,to predict the“fuzzy”conduction band,the full band,and the band gap for the one-dimensional polymer of polyyne molecules.

(3)The cumulative polyene molecules may have even or odd numbers of C-atoms.The one with even C-atoms has a planar structure,and its π-MOs that are perpendicular to the molecular plane are not degenerate with those in the plane.So,the characteristic curves of the membership functions of the two kinds of π-MOs about translation symmetry transformation and their MO energy must be investigated.

(4)The cumulative polyene molecule with odd numbers of C-atoms has a non-planar structure.Their two kinds of π-MOs just mentioned are perpendicular to each other and degenerate.So,it is feasible to investigate the characteristic curves of the membership function and the MO energy for only one kind of the π-MOs.However,these polyene molecules do not have the usual symmetry center,so that the fuzzy symmetry about their central symmetry is now explored in this paper.Also,we have given out the characteristic curve of the membership function of the central inverse transformation as well as the distribution patterns of the irreducible representation(symmetry and anti-symmetry representation),about the center inverse transformation.

(5)Carbon-carbon straight chain and ring chain formed by m C-atoms will have similarity at some aspects and to a certain extent based on the Born-Karman approximation.That is,the parallel translation symmetry of the former is isomorphic with the m-flod rotational symmetry of the latter.Here,we investigate the full carbon ring molecule Cm.Though the full carbon ring molecule has the Dmhsymmetry,it can be analyzed by the point group Cmin many cases,due to the above isomorphism relation. The MOs which belong to the one-dimensional irreducible representation of these point groups are the eigenstates of all the symmetry transformations and their membership functions are all 1.For MOs belonging to the two-dimensional irreducible representation in relation to Dmh,they are not always the eigenstates of all the symmetry transformations.Moreover,when the full carbon ring molecule Cmis treated with some symmetry transformations,we can only discuss their fuzzy symmetry and sometimes their membership functions are less than 1.The MOs which have the same two-dimensional irreducible representations will share similar corresponding membership functions by each other.

(6)For the full carbon ring molecules,we take the C6and C18molecules as examples and adopt the cylindrical coordinates to explore them.That is,the corresponding p-AOs are pz-,pr-and pt-AO,where z and r represent the axial and radial directions,respectively,in the cylindrical coordinates.Here,t is orthogonal with z and r,and can be denoted as the tangential direction.The two kinds of π-MOs mainly comprised SALC-pz-AO and SALC-pr-AO sets.The latter sometimes contains a considerable degree of other SALC-p-AO components.In spite of containing different SALC-p-AO components,these MOs belonging to this onedimensional irreducible representation are the eigenstates of all the symmetry transformation and the membership functions are all 1.For MO belonging to two-dimensional irreducible representation,we can only discuss the fuzzy symmetry for some symmetrytransformationanditsmembershipfunctionis less than 1.For MOs containing the same two-dimensional irreducible representation,their corresponding membership functions are similar.

1 Mezey,P.G.;Maruani,J.Mol.Phys.,1990,69:97

2 Mezey,P.G.;Maruani,J.Int.J.Quantum Chem.,1993,45:177

3 Mezey,P.G.J.Math.Chem.,1998,23:65

4 Maruani,J.;Mezey,P.G.Compt.Rend.Acad.Sci.Paris(Série II), 1987,305:1051

5 Maruani,J.;Toro-Labbé,A.Compt.Rend.Acad.Sci.Paris(Série IIb),1996,323:609

6 Mezey,P.G.Int.Rev.Phys.Chem.,1997,16:361

7 Zabrodsky,H.;Peleg,S.;Avnir,D.J.Am.Chem.Soc.,1993,115: 8278

8 Avnir,D.;Zabrodsky,H.;Hel-Or,H.;Mezey,P.G.Cyclopaedia of computational chemistry.Vol.4.von Ragué Schleyer,P.Ed. Chichester:Wiley,1998:2890-2901

9 Chauvin,R.J.Math.Chem.,1994,16:245

10 Chauvin,R.J.Math.Chem.,1994,16:257

11 Zhou,X.Z.;Fan,Z.X.;Zhan,J.J.Applicationoffuzzymathematics inchemistry.Changsha:National University of Defence Technology Press,2002:325-349 [周旭章,范真祥,湛建阶.模糊数学在化学中的应用.长沙:国防科技大学出版社,2002:325-341]

12 Zhao,X.Z.;Xu,X.F.Acta Phys.-Chim.Sci.,2004,20:1175 [赵学庄,许秀芳.物理化学学报,2004,20:1175]

13 Zhao,X.Z.;Xu,X.F.;Wang,G.C.;Pan,Y.M.;Cai,Z.S.Mol. Phys.,2005,103:3233

14 Xu,X.F.;Wang,G.C.;Zhao,X.Z.;Pan,Y.M.;Liang,Y.Y.; Shang,Z.F.J.Math.Chem.,2007,41:143

15 Zhao,X.Z.;Xu,X.F.;Wang,G.C.;Pan,Y.M.;Shang,Z.F.;Li, R.F.J.Math.Chem.,2007,42:265

16 Zhao,X.Z.;Wang,G.C.;Xu,X.F.;Pan,Y.M.;Shang,Z.F.;Li, R.F.;Li,Z.C.J.Math.Chem.,2008,43:485

17 Zhao,X.Z.;Shang,Z.F.;Wang,G.C.;Xu,X.F.;Li,R.F.;Pan,Y. M.;Li,Z.C.J.Math.Chem.,2008,43:1141

18 Zhao,X.Z.;Shang,Z.F.;Sun,H.W.;Chen,L.;Wang,G.C.;Xu, X.F.;Li,R.F.;Pan,Y.M.;Li,Z.C.J.Math.Chem.,2008,44:46

19 Zhao,X.Z.;Xu,X.F.;Shang,Z.F.;Wang,G.C.;Li,R.F.Acta Phys.-Chim.Sci.,2008,24:772 [赵学庄,许秀芳,尚贞峰,王贵昌,李瑞芳.物理化学学报,2008,24:772]

20 Li,Y.;Zhao,X.Z.;Xu,X.F.;Shang,Z.F.;Zhou,Z.;Cai,Z.S.; Wang,G.C.;Li,R.F.Sci China Ser.B-Chem.,2009,52:1892

21 Zhao,X.Z.;Shang,Z.F.;Li,Z.C.;Xu,X.F.;Wang,G.C.;Li,R. F.;Li,Y.J.Math.Chem.,2010,DOI:10.1007/s10910-010-9660-z

22 Mlder,U.;Burk,P.;Koppel,I.A.J.Mol.Struct.-Theochem,2004, 712:81

23 Zhao,C.D.Quantum chemistry of solids.2nd ed.Beijing:Higher Education Press,2003:51-54,197-204 [赵成大.固体量子化学.第二版.北京:高等教育出版社,2003:51-54,197-204]

24 Wang,R.H;Gao,K.X.Symmetry group of crystallography. Beijing:Science Press,1990:348-349 [王仁卉,郭可信.晶体学中的对称群.北京:科学出版社,1990:348-349]

25 Dietmar,A.;Plattner,K.N.H.J.Am.Chem.Soc.,1995,117:4405

26 Parasuk,V.;Almlof,J.;Feyereisen,M.W.J.Am.Chem.Soc., 1991,113:1049

27 Jeffrey,G.A.;Rollett,J.S.Proc.R.Proceedings of the Royal Society of London Series A-Mathematical and Physical Sciences, 1952,213:86

28 Molder,U.;Burk,P.;Koppel,I.A.Int.J.Quantum Chem.,2002, 82:73

29 Weimer,M.;Hieringer,W.;Della Sala,F.;Gorling,A.Chemical Physics,2005,309:77

30 Wakabayashi,T.;Nagayama,H.;Daigoku,K.;Kiyooka,Y.; Hashimoto,K.Chem.Phys.Lett.,2007,446:65

31 Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03. Revision B.01.Pittsburgh,PA:Gaussian Inc.,2003