GW方法:基本原理,最新进展及其在d-和f-电子体系中的应用

蒋 鸿

(北京大学化学与分子工程学院理论与计算化学研究所,稀土材料化学及应用国家重点实验室,北京分子科学国家实验室,北京 100871)

GW方法:基本原理,最新进展及其在d-和f-电子体系中的应用

蒋 鸿*

(北京大学化学与分子工程学院理论与计算化学研究所,稀土材料化学及应用国家重点实验室,北京分子科学国家实验室,北京 100871)

基于格林函数的多体微扰理论提供了描述材料基态和激发态性质的一个严格理论框架.格林函数依赖于交换关联自能,后者满足一组复杂的被称为Hedin方程的积分微分方程.GW方法是由对自能算符根据屏蔽库仑作用做多体微扰理论展开到第一项得到,是目前描述扩展体系准粒子电子激发性质最为准确的第一原理方法.本文概述了GW方法的基本原理,并对最新的理论方法进展在一个统一的框架下进行了评述.最后,通过对若干典型实例的分析展示了针对d/f-电子体系的GW方法的现状.

多体微扰理论;GW近似;准粒子电子结构;d/f-电子体系;强关联电子体系

Kohn-Sham(KS)density functional theory(DFT)[1-2]in the local density or generalized gradient approximation(LDA/GGA) to the exchange-correlation(xc)energy functional has become“the standard model”for first-principles electronic structure calculations of extended systems[3],mainly because they can provide accurate descriptions for energetic and structural properties of many materials within feasible computational efforts.By mapping the interacting system to a fictitious non-interacting (Kohn-Sham)system that has the same ground state electron density as the interacting one,the original highly complicated many-bodyproblem istransformed to solvinga single-particle equation that is formally resembles a mean-field theory,but is ex-act in principles.Rigorously speaking,the KS single-particle energies and wave functions in general do not have any physical meanings,but in practice they are often used to interpret excited state properties as probed by direct and inverse photo-emission spectroscopy and optical absorption.This practice,however,can only be exercised with caution.Even for weakly correlated systems such as sp semiconductors,the KS-DFT within LDA/GGA gives band gaps that are systematically underestimated when compared to experiment,and can predict metallic ground state for small-gap semiconductors,e.g.,Ge,InN and so on.The problem can become even more severe for systems with open d-or fshell,often called strongly correlated systems,for which even wide gap insulators can be predicted to be metallic.Other ground state properties like magnetic ordering can also be qualitatively wrong in LDA/GGA descriptions.This is best illustrated in the notorious failure of the LDA/GGA for late 3d transition metal oxides[4].

The difficulty of the LDA/GGA for d/f-electron systems is actually common for all mean-field band-theory based approaches, which was already realized soon after the birth of the band theory.As a result,the“standard”theoretical approaches for strongly correlated d/f-electron systems are often based on some highly simplified model Hamiltonian,such as the Anderson impurity model[5]and the Hubbard model[6],which usually aims to represent only a particular aspect of the system under study,and neglect all other,usually materials specific,details.These model approaches are very useful to analyse experimental data in simple pictures.Some of these models,in spite of its formal simpleness,can have very rich physics,and in the meanwhile theoretically highly demanding.Nevertheless the model Hamiltonian approaches are usually not first-principles and often rely on empirical parameters.In the recent years,a lot of efforts have been invested to develop first-principles approaches beyond LDA/ GGA in the DFT framework that can treat d/f-electron systems correctly.The most widely used correlated band theory approaches,as they are often called,are the LDA+U[7-8],the selfinteraction corrected LDA[9-11],and hybrid functionals approaches[12-13].These approaches can dramatically improve the descriptions of many d/f-electron systems within reasonable computation efforts,but at the price of a certain conceptual rigorousness. For example,the LDA+U approach relies on the system-specific parameter U,the on-site Coulomb interaction term,which is difficult,if not impossible,to be uniquely determined,and in practice is often treated as an empirically adjustable parameter.Even more serious is that these correlated band theory approaches mainly aim to improve the descriptions of ground state properties.The quality of the single-particle spectrum from these approaches is not guaranteed by their improvement of the ground state properties.Compared to the ground state properties,excited states properties are more strongly dependent on proper treatment of correlation effects,even for weakly correlated sp systems.

Excited states properties can in principles be described exactly in the framework of the time-dependent density functional theory(TDDFT)[14-15],in which the central quantity is the exchange-correlation kernel,fxc,corresponding to the second order functional derivative of the xc energy functional with respect to electron density in a time-dependent framework.For many finite systems,even the simplest approximation to the xc kernel,the adiabatic local density approximation(ALDA),can already give very accurate optical excitation properties.But the ALDATDDFT method,like its static counterpart,has serious limitations[16].It significantly underestimates charge-transfer type excitation energies,and has difficulty in describing multi-electron excitations.For extended systems,the ALDA-TDDFT has more seriousproblems[17-18].Recentyearshave seen promisingprogresses to overcome these difficulties in the TDDFT for solids[17-18], but substantial efforts are still needed.Furthermore,the TDDFT is formulated mainly to describe neutral(optical)excitation. Quasi-particle excitations,as probed by photoemission and inverse photoemission spectroscopy,can not be accessed straightforwardly in the TDDFT framework.

Electronic quasi-particle excitations are best described by the many-body perturbation theory based on the one-body Green′s function[19-20].The central quantity is the exchange-correlation self-energy,Σxc,which is non-local,energy-dependent and nonhermitian,and includes all non-classical electron-electron interaction effects.Exact Σxccan be obtained by solving a set of complicated integro-differential equations,Hedin′s equations after Hedin[19],which is unfortunately out of reach even for the simplest systems like homogeneous electron gas(HEG).Therefore one has to resort to various approximations.The state-of-the-art approach is the GW approximation(GWA),which is the first order term in a systematic many-body perturbation expansion of Σxcwith respect to the screened Coulomb interaction W.In practice,a“best G best W”strategy is usually used,where the quasiparticle energies are calculated as a first-order correction to some reference single-particle Hamiltonian H0,and both G and W are calculated using eigen-energies and eigen-functions of H0, hence called G0W0.

The G0W0method based on the LDA H0,denoted henceforth as G0W0@LDA,has become the method of choice for the description of quasi-particle band structures in weakly correlated solids[20].However,its applications,and even its validity to d/ f-electron systems are still far from established.The difficulty first arises from the failure of the LDA for d/f-electron systems so that a perturbative treatment based on the LDA single-particle Hamiltonian is no longer adequate any more.Obviously the failure of G0W0could be due to either the failure of LDA H0as the starting point,or the GW approximation itself.On the other hand,the fully self-consistent GW,besides its formidable computational demand,is also problematic because a self-consistency without including higher order contributions beyond the GW approximation to the self-energy is internally inconsistent.The latter seems to be confirmed by recent investigations of homogeneous electron gas,where it was found that although the ground state energy is significantly improved by using self-consistently obtained Green′s function within GWA,the quasi-particle properties are significantly worsened.An unambiguous evaluation of the GW approximation for d/f-electron systems is therefore anything but trivial.The main strategy that is currently under intensive investigation is to develop better reference single-particle Hamiltonian[21-25]including,in particular,to construct H0based on the GW approximation itself[22-24].As such a construction is not unique,one can only evaluate its performance by systematic investigations against reliable experiment data,and for simple model systems,by comparing to other more accurate theoretical results.

The main aim of this paper is three-fold:1)to provide an overview of the many-body perturbation theory for quasi-particle excitations based on the Green′s function and screened Coulomb interaction;2)to review the latest methodological developments in a unified framework;and 3)to showcase the current status of the GW method for d/f-electron systems by a few prototypical examples.

1 Fundamentals of the GW method

In this section we are going to formulate the many-body perturbation theory based on the one-body Green′s function and screened Coulomb interaction in a concise but nevertheless selfcontained manner.More complete formalisms can be found in Refs.[20,26-27].

1.1 Challenges to theoretical description of direct and inverse photo-emission spectroscopy

Electronic properties of a material(finite or extended)are most often investigated by measuring the response of the system under study to some external perturbation,using either electron or photon as the probe.Among the most widely used spectroscopic techniques are photo-emission,inverse photo-emission and optical absorption spectroscopic methods.In the photoemission spectroscopy(PES),photons with given energy impinge on the sample and electrons are ejected.By monitoring the kinetic energy of photoelectrons,the properties of electronic occupied states can be measured.In the inverse photo-emission spectroscopy(IPS),the procedure is reversed:electrons with a certain energy are injected into the sample and fill into originally unoccupied states;the abundant energy then radiates as photons, whose intensity distribution reveals the information of unoccupied states.In essence,PES and IPS measure single-particle excitations of the system,with the total electron number N changing to N-1 or N+1,which are often termed as quasi-particle (QP)excitations.The optical absorption spectroscopy(OAS),on the other hand,measures neutral excitations,in which electrons are excited from an occupied state to an unoccupied one,creating a hole and an electron simultaneously,and the electron-hole interaction often plays an important role.Physical processes involved in PES,IPS and OAS are illustrated in Fig.1.

The main topic of this review is the theoretical description of QP excitations as probed by the PES and IPS.Due to strong Coulomb interaction among electrons,in principles one needs to solve a truly many-body problem for the N and(N±1)-electron systems,including both their ground states and excited states using ab initio post-Hartree-Fock quantum chemistry methods or quantum Monte Carlo.Such rigorous many-body approaches are,however,only feasible for small finite systems or simple model systems like homogeneous electron gas.In practice,one usually uses some highly simplified mean-field approach,most notably Hartree-Fock(HF)or Kohn-Sham single-particle Hamiltonian,to interpret PES/IPS and OAS data[28-29].In the HF theory, the orbital energies can indeed be interpreted as one-electron removal and addition energies(Koopman′s theorem),but under the assumption that HF orbitals are not relaxed as an electron is removed from or added to the system,which is,of course,a crude approximation in most cases.The main physics that is missing in the HF is the screening effect of Coulomb interaction, which is the reduction of the effective interaction between two electrons due to the presence of other electrons.As a result,the HF theory completely fails for metallic systems,and for insulat-ing systems,dramatically overestimates the band gap.

Fig.1 Schematic illustration of photo-emission,inverse photo-emission and optical absorption spectroscopy(courtesy of Dr Patrick Rinke)

In the KS-DFT,the situations are more complicated.Rigorously speaking,the KS orbital energies and wave-functions are auxiliary quantities corresponding to a fictitious non-interacting system that is introduced only to obtain the ground state total energy and electron density of the interacting system.There is no physical justification to interpret KS orbital energies as quasiparticle energies except for the highest occupied Kohn-Sham orbital energy.The latter corresponds to the ionization potential under the condition that the exact exchange-correlation potential is used[28].Nevertheless,the Kohn-Sham single-particle Hamiltonian(H),due to its conceptual simplicity,is often used to describe QP excitations.However,the mean-field aspect of Himplies that such a treatment is in principle deficient[29],since single-particle excitation as probed by PES/IPS intrinsically involves many-body interaction effects,and in practice it leads to the“DFT band gap problem”.On the other hand,KS-DFT,as a many-body theory for the ground state total energy,does provide access to the special case of the fundamental band gap,εgap, which can be identified to the second order difference of the ground state total energy with respect to electron number.

In the KS-DFT framework,εgapcan be decomposed into two contributions:

where∈gapis the KS band gap,i.e.,the difference between the energies of highest occupied and lowest unoccupied KS molecular orbital(HOMO-LUMO),and Δxcis the N-derivative discontinuity of the xc functional[28,30].It has been proved,based on general formal analysis,that Δxccorresponding to the exact xc functional must be finite[28].However,all approximate xc functionals that explicitly depend on electron density(or more generally,spindensities)are continuous function of electron number,i.e.,Δxc=0. Finite Δxccan be obtained from orbital-dependent implicit xc functionals,and the corresponding Δxcstrongly depends on the underlying approximation[31-34].For example,in the simplest implicit xc functional,the exact-exchange(EXX)-only approximation,which is just the Fock exchange energy calculated by KS orbitals,the KS band gap shows apparently good agreement with experiment for many materials including sp semiconductors[32]and later transition metal oxides[35],but after including Δxc,the resultant DFT fundamental gaps become nearly identical to those of the Hartree-Fock(HF)[32].Practical implementations of implicit xc functionals can be cumbersome since the corresponding xc potential has to be calculated by solving a complicated integral equation through the optimized effective potential (OEP)method[36],which is already non-trivial for the simplest EXX-only case[36]and can become formidably complicated for more general cases[37-38].Recently Yang and coworkers have shown that the fundamental band gap for a given implicit functional can be calculated in the framework of the generalized Kohn-Sham theory with the total energy minimized with respect to the single-particle orbitals[39].

Recent developments in DFT have shed promising light on the possibility to obtain accurate fundamental band gaps within the KS-DFT framework.On the other hand,it remains to see whether the formalism can be generalized to full single-particle excitation spectrum as probed by the PES/IPS measurement. Conceptually it is much simpler to describe single-particle excitations in terms of electron and hole quasi-particles(QP)energies εnand wave functions Ψn(r),which are solutions of the following QP equation(atomic units are used through the paper)

To simplify the notation,we drop the wave-vector(k)dependence of all quantities through the paper,which is implied for extended systems without saying.In Eq.(3),Vext(x)and VH(x)are the external and Hartree potential,accounting for electron-nuclei interaction and classical electron-electron(e-e)Coulomb interaction,respectively;Σxc(x,x′;ε)is the exchange-correlation selfenergy that is non-local,energy-dependent and non-hermitian accounting for all non-classical many-body interaction effects. Note we use x≡(rs)to represent both spatial(r)and spin(s)degrees of freedom of electrons.In the following sections,we are goingto formulate how to calculate Σxc(x,x′;ε)in the many-body perturbation theory.

1.2 Green′s function and its equation of motion

We start from the Hamiltonian of the interacting system, which,in the second-quantization representation,reads[40],

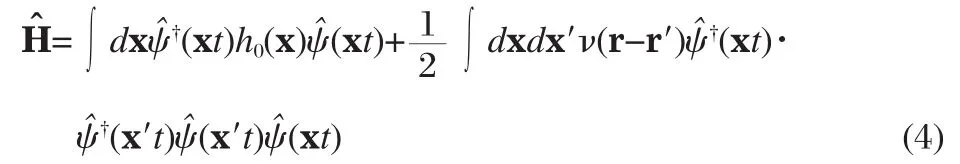
One-body Green′s function G(xt,x′t′)is defined as[40]

where T is the time-ordering operator.Using the Heisenberg equation of motion(EOM)for the field operator

we can obtain the equation of motion for the Green′s function

Using the two-body Green′s function

Eq.(7)can be written as

with t+≡t+η,where η is an infinitesimal positive number,introduced to keep right order of the field operators in the two-body Green′s function.We see that the equation of motion for the one-body Green′s function involves the unknown two-body Green′s function.A similar equation of motion can also be obtained for G2,which depends on the three-body Green′s function.The formulation continues,leading to a infinite series of coupled equations in the end.

Eq.(9)can be used as the starting point for various approximations.For example,the Hartree approximation can be obtained by approximating G2as

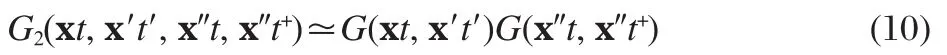
and the Hartree-Fock(HF)approximation is obtained by

It is very hard to incorporate high order approximations directly based on Eq.(9).As far as one-body excitation is concerned,it is formally more convenient to reformulate Eq.(9)in terms of the self-energy.

1.3 The self-energy and quasi-particle equation

Formally the exchange-correlation self-energy Σxcis defined as

so that the equation of motion for the Green′s function now reads

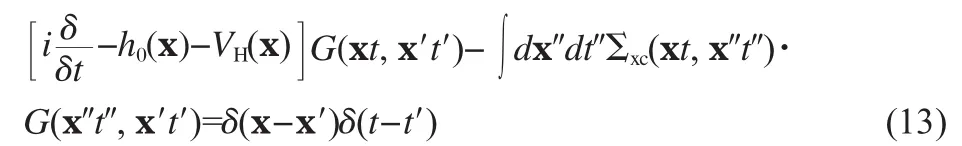
Eq.(13)is formally equivalent to the original EOM formalism using two-body Green′s function,with all complexities related to the two-body and higher order Green′s functions all wrapped up in the self-energy operator Σxc.The physical meaning of Σxccan be more easily appreciated by working in the frequency domain,assuming that the system under study has no explicit timedependence,

We then obtain

where H0≡h0+VH.In the matrix notation,one has,

Using the zero-order approximation to G,obtained from neglecting the second term in the equation above,

we have

which is the well-known Dyson′s equation for the Green′s function.

Up to now we have formulated everything in terms of the (one-body)Green′s function,from which one can,in principles, obtain all ground state single-particle properties,single-particle excitation properties(N➝N±1)as well as the ground state total energy[40].As far as the single-particle excitation is concerned,it is more convenient to work directly with the so-called quasi-particle energies and wave functions.According to the Green′s function theory of the differential equations[20,41],the Green′s function G(x,x′;ω)as the solution of Eq.(15)can be formally written in the following form

where Ψn(x;ω)and εn(ω),often called QP wavefunctions and energies,are the eigen-solutions of the following equation

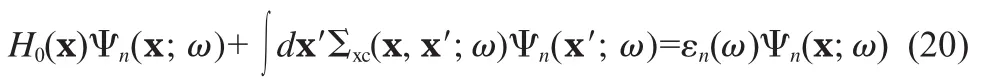
By definition,ω is real,but formally it is more convenient to extend the domain of ω to the whole complex plane by analytic continuation,so that the poles of G(x,x′;ω),with ω=εn(ω),correspond to quasi-particle energies.Since QP energies and wave functions are the main quantities we are interested in,we can replace Eq.(20)by

Eq.(21)is usually denoted as the QP equation,which is the working equation that we are going to use in the remaining part of this paper.It is important to point out that we use the term“quasi-particle”in its generalized sense.In a more specialized sense,a QP state refers to a solution of Eq.(21)εnwith a vanishing(or very small)imaginary part.

1.4 Hedin′s equations

The self-energy operator is itself a complicated quantity. There are mainly two approaches to obtain approximate Σxcin a computationally accessible way:1)Feynman′s diagrammatic approach based on Wick′s theorem[40],and 2)Schwinger′s the functional derivative method[27].The former is widely used for finite systems,in the so-called electron propagator theory[42],where the screening among electrons is weak,and a many-body expansion with respect to the bare Coulomb interaction up to the second order often gives very accurate descriptions.For extended systems with strong screening among electrons,the second approach,in the form of a set of coupled integral equations involving screened Coulomb interaction(Hedin′s equations),is more appropriate,and is the subject of this work.Hedin′s equations, as first formulated by Hedin using the functional deriva tive techniques[19],relate the self-energywith the dynamicallyscreened Coulomb interaction W,and,when calculated perturbatively, lead to a many-body perturbation expansion with respect to W instead of ν.The full derivation of Hedin′s equations is quite complicated,but the basic ideas are actually quite simple.In this paper,we will outline the essence of the derivation.A more detailed formulation can be found in Refs.[26-27].

The crucial point of the functional derivative approach for the self-energy is that the two-body Green′s function appearing in the definition of the self-energy can be related to the response of one-body Green′s function G(1,2)(The abbreviation 1≡(x1t1)is used to simplify the notation)with respect to the small external potential φ(xt)introduced into Eq.(9)in an adiabatic manner[27]

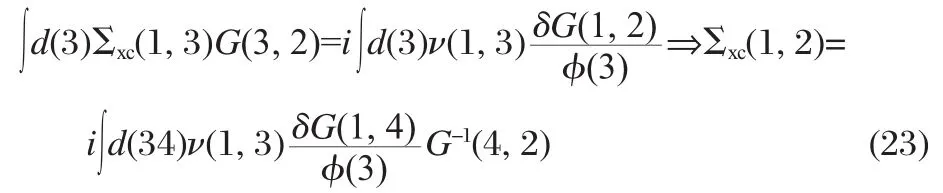
From some simple formal manipulations(in the matrix form)

Using the last equation we obtain

Now defining V(1)≡VH(1)+φ(1),and using the chain rule we have

where we have introduced the inverse dielectric function

the vertex function

and the screened Coulomb interaction

Now let′s introduce the polarization function P,defined as

Using the relation between the electron density ρ(1)and Green′s function ρ(1)=-iG(1,1+)we can obtain the equation for P

where the second equality is obtained by using the same technique as in Eq.(24).We can obtain the relation between the polarization function P and the dielectric function by some formal transformation(again using the matrix form to simplify the notation)

From the last equation we obtain

Using the relation between P and ε-1(the last equality of Eq. (32)),we can also obtain the integral equation for the screened Coulomb interaction W

Now the only missing piece is a Dyson-like equation for the vertex function Γ(1,2,3),which can also be obtained straightforwardly by formally inverting the equation of motion for G(Eq. (13))

Now putting all pieces together,we obtain the following set of coupled equations,

which,together with the Dyson′s equation for Green′s function (Eq.(18)),form a closed set of integral equations as illustrated in Fig.2.

1.5 GW approximation

Hedin′s equations for the self-energy are highly complicated, and are not solvable even for the simplest systems like the homogeneous electron gas.The real power of Hedin′s equations is that it provides the starting point for a many-body perturbation theory(MBPT)in terms of the screened Coulomb interaction W, which would converge much faster compared to the MBPT in terms of the bare Coulomb interaction.The most widely used approximation based on Hedin′s equation is the so-called GW approximation,which is obtained by taking the zero-order approximation for the vertex function

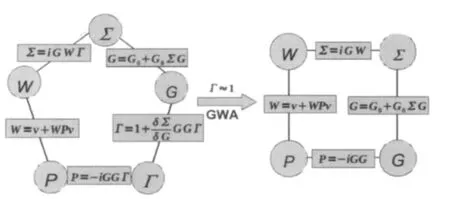
Fig.2 Schematic illustration of Hedin′s equations in the full form(left)and within the GW approximation(right)

In this case,the self-energy becomes a simple product of the Green′s function G and screened Coulomb interaction W,hence the term GW,

A positive infinitesimal has been introduced in the equation above as needed for the bare exchange self-energy[20]

The last equality is from the Feynman′s rules[40],G(x1t1;x2t2=t1)≡G(x1t1;x2t+1).Using the zero-th order vertex function,the polarization function is simplified to be the product of two Green′s functions,which is often called random-phase approximation (RPA)of P.

The physical picture underlying the GW approximation is illustrated in Fig.3.The GW self-energy in the frequency domain reads

Fig.3 Schematic illustration of the GW approximation using the Feynman diagram Courtesy of Dr.Patrick Rinke

The GW self-energy,as the first-order term in a systematic many-body perturbation theory expansion with respect to the dynamic screened Coulomb interaction W,is formally very similar to the HF self-energy that is the first term obtained from the MBPT expansion with respect to the bare Coulomb interaction ν.As a result of screening,the interaction described in GW is much weaker and shorter ranged compared to the bare Coulomb interaction.In the semi-classical(Thomas-Fermi)limit,W can be approximated as W⋍e-λr12/r12where λ is the Thomas-Fermi screening parameter characterizing the effective screening range[27].The screening is especially important for metallic systems for which the HF theory fails dramatically,leading to,e.g., infinite density of states at the Fermi level in homogeneous electron gas[27].The other equally important feature of W is its energy dependence,which make GW different from the screened exchange LDA(sxLDA)[45]and screened hybrid functionals[13,46]. The latter approaches take the screening effect into account by using a parameterized screened Coulomb interaction,and have achieved remarkable successes to improve the LDA/GGA descriptions of a wide range of materials and properties[13].In a recent systematic study of the exchange-correlation effects in the sxLDA method in comparison with GW[47],it was found that although both sxLDA and GW reproduce experimental band gaps very well for a set of sp-systems,the underlying physics is different.The sxLDA improves the LDA band gap mainly by the downward shift of valence band states,whereas in the GW the corrections for the conduction band states are also important. This can have significant effects on the relative level alignment in semiconductor heterojuctions or molecule-solid interfaces[48].

1.6 G0W0approach

Formally Hedin′s equations even within the GW approximation are still very complicated,as illustrated in Fig.2,involving self-consistent construction of the GW self-energy using the solution of Dyson′s equation,which is non-Hermitian,and therefore mathematically cumbersome to tackle.In practice,further approximations are usually introduced based on a“best G,best W”strategy,in which both G and W are calculated using eigenenergies∈nand eigen-functions ψnof some Hermitian single-particle Hamiltonian,H0,hence called the G0W0or one-shot GW approach,

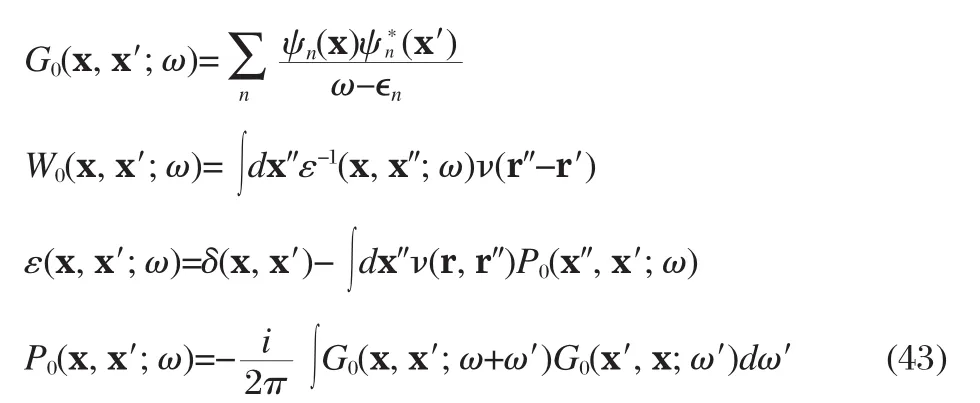
The QP energies εnare calculated by the first order perturbation theory,treating δΣxc≡Σxc-Vxcas the perturbation

where Vxcis the exchange correlation potential already included in H0,and Znis the QP renormalization factor,

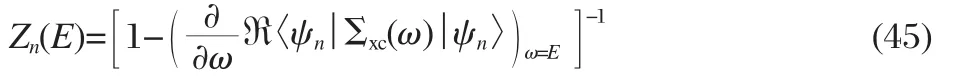
accounting for the frequency dependency of Σxc.For sp-semiconductors it has been demonstrated that further improvement can be obtained by introducing partial self-consistency with little computational overhead.In the so called eigenvalue self-consistent GW0approach the energy denominator in the Green′s function is updated by εn′s,but W remains unchanged[49].

In principles,the reference single-particle Hamiltonian H0should be chosen to give the best possible approximation for G and W.For extended sp-electron systems,the LDA/GGA KS single particle Hamiltonian is the most popular choice in practice.We note,however,that using the KS H0as the zeroth order reference for GW calculations is mainly based on pragmatic considerations without much formal justifications since the KS singleparticle energies in general can not been identified as the quasiparticle energies,even at an approximate level.On the other hand,the LDA/GGA can often describe the dispersion of quasiparticle band structures very accurately,although the band gaps are significantly underestimated.Formally the HF single-particle Hamiltonian is more appropriate as the GW starting point since the HF energies can be related to quasi-particle excitations in terms of Koopmans′s theorem,although in a quite crude manner.However,the HF descriptions of metals and semiconductors are usually much less satisfactory than the LDA/GGA ones due to its failure to treat the screening(dynamic correlation)effect properly.For wide-gap insulators or finite molecular systems,in which the screening is usually very weak,the HF H0might become more appropriate.However,since the implementation of the HF method for extended systems is much more demanding, most G0W0calculations use LDA H0as the starting point.As we will discuss in the next section,the LDA/GGA H0becomes inadequate for d/f-electron systems for which LDA/GGA often fails qualitatively.

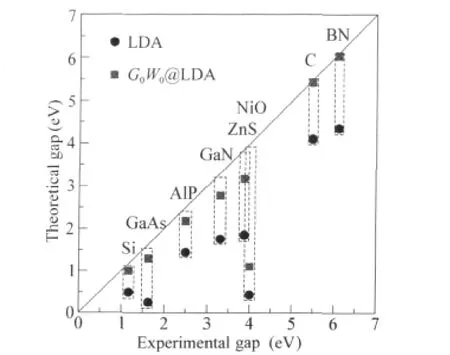
Fig.4 Band gaps from LDA and G0W0@LDA for a selected set of prototypical semiconductors and insulators compared to experimentLDA band gaps were obtained by using the full-potential linearized augmented plane wave(LAPW)method as implemented in the WIEN2k package[43].G0W0@LDA results were obtained from the all-electron LAPW GW code recently developed by Gomez-Abal et al.[44].

The G0W0approach based on the LDA single-particle Hamiltonian has achieved remarkable success for sp semiconductors and insulators since its first applications for real materials in 1980′s[50-51].In contrast to the dramatic underestimation of LDA gaps,G0W0@LDA band gaps are typically within 0.1-0.2 eV of the experimental values.This remarkable success turns out to be partly thanks to the error cancellation due to the use of the pseudo-potential approach in most of these studies.Recent more systematic studies using more accurate all-electron approaches[44,52-53]indicate that the G0W0@LDA approach exhibits a systematic underestimation by 0.1-0.2 eV for normal sp semiconductors,and the error can become slightly larger for systems with semicored states.Fig.4 shows band gaps of a selected set of materials from the LDA and G0W0@LDA compared to experiment.Several features revealed in this plot are typical.1)In general G0W0dramatically improves the LDA band gaps,leading to overall good agreementwith experiment,with a small systematic error of-0.1 to-0.2 eV.2)For materials with shallow semi-core d-states such as GaAs and ZnS,the errors in the G0W0band gaps are usually significantly larger,up to:ca-0.5 eV or even larger.Even more seriously,G0W0underestimates the d-states binding energy in these materials by up to a few eV.3)G0W0@LDA fails badly for systems with partially occupied d-or f-shells.For NiO in the type-II anti-ferromagnetic phase,LDA gives a band gap:ca 0.4 eV,almost one-order of magnitude smaller than the experiment value,and G0W0@LDA only slightly improves the LDA results. For more general d/f-electron systems,LDA often gives qualitatively wrong descriptions,and so does G0W0@LDA.

2 Recent methodological developments

Although the approximations made in G0W0@LDA are adequate for many weakly correlated sp semiconductors and insulators,one can expect that they could fail for more strongly-correlated systems.The failure of G0W0@LDA can be attributed to two possible causes:the inadequacy of LDA single-particle spectrum as the input for G0W0calculations,or,more dramatically,the failure of the GW approximation itself,i.e.,higher order correlation effects become important.Of course,how to differentiate the two aspects is anything but trivial.In this section we will review some latest methodological developments.

2.1 Full self-consistent GW

The G0W0method has the major drawback that it depends on the reference single-particle Hamiltonian H0from which G0and W0are calculated.In addition,the lack of self-consistency also results in the violation of the conservation of particle number and energy when the system under study is subject to external perturbations[20].These problems can be avoided by using the GW method in a self-consistent way,as illustrated in Fig.2.As proved by Baym and Kadanoff[54-55],a conserving Green′s function has to meet the requirements that it has to be a self-consistent solution of the Dyson′s equation with the corresponding self-energy being derivable from the Luttinger-Ward(LW)energy functional Σxc[G]=δΦ/δG.However,full self-consistent GW (SCGW)calculations are mathematically complicated and computationally very demanding,due to the fact that the self-energy operator is non-local,non-Hermitian and energy dependent.As a result,the solutions of the QP equation are not orthonormal, and they can not be obtained by standard linear algebra techniques.On the other hand,the full SCGW does not necessarily provide more accurate QP properties.The full self-consistency for G can surely improve the ground state total energy due to the variational nature of the LW functional,but quasiparticle properties are not variational.From a conceptual point of view,a selfconsistent solution of the Hedin′s equations with the GW approximation to the self-energy would successively introduce higher order electron-electron interaction terms of certain types without a balanced treatment of other higher order terms con-tained in the vertex function.

Whether the full self-consistency improves or deteriorates quasi-particle properties has been under fierce debate in recent years.The first full SCGW calculation was undertaken for a quasi-one-dimensional model semiconductor[56].Although the relevance of such a highly simplified model system to real materials seems to be rather weak,the main features revealed in this study are very illuminating.The band gaps obtained from the full SCGW were found to be very close to the Hartree-Fock gaps,probably due to much weaker screening in 1D systems than that in 3D bulk systems.Compared to the quantum Monte Carlo results,the full SCGW gaps are significantly overestimated,indicating that the vertex corrections are important in this model system.

The partial and full SCGW(GW0and GW,respectively)are also applied to homogeneous electron gas[57-59].It was found that by introducing self-consistency,the band width of the HEG is increased with respect to the non-self-consistent value,and therefore deviates more severely from that of the experimental value for the alkali metals.The self-consistency also increases the weight of the quasi-particle peak;concomitantly the plasmon satellite is broadened and shifted towards to the Fermi energy, and almost disappears in the full SCGW.Qualitatively similar features were also observed in full SCGW studies of real nearlyfree-electron-(NFE)-like metals K[60]and Al[61].

The full SCGW has also been applied to simple semiconductors like Si and Ge by several groups[52,60-62].Different groups obtained dramatically different band gaps for such simple systems like Si,an indication of the complexity of the issue.In Ref.[60], a fundamental gap of 1.91 eV is obtained by the full SCGW,in contrast to the experimental value of 1.17 eV(G0W0@LDA gives 1.34 eV in the same work).A possible cause of this dramatic overestimation is the use of the pseudo-potential[44,52-53].Ku and Eguiluz reinvestigated the full SCGW band gap of Si using an all-electron LAPW approach,and obtained a gap of 1.03 eV,apparently in good agreement with the experimental value[52].However,in this study,only 14 bands(10 unoccupied)were used.As discussed in Refs.[44,53],the convergence of the GW band gap with respect to the number of unoccupied bands used is actually quite slow,and the results obtained from 10 bands are probably not converged.In another full SCGW study,also using the LAPW approach,Kutepov et al.[61]obtain a gap of 1.55 eV for Si.We should also mention the work by Zein et al.[62],who developed a local self-energy approach using the linearized muffin-tin orbital(LMTO)method within atomic sphere approximation(ASA)to perform full SCGW calculations,and obtained a gap of 1.10 eV.The accuracy of this approach is,however, doubtful,as indicated by the fact this approach gives a G0W0@LDA gap of only 1.33 eV for AlAs,significantly different from other all-electron G0W0studies.The fact that different groups obtain severely disparate full SCGW results for such simple systems like Si is very disturbing,indicating clearly that further systematic and benchmark studies are needed.

2.2 Approximate self-consistent GW

To avoid the computational complication of the full SCGW, recently there have been intensive efforts to developing approximate self-consistent GW.To put these apparently different schemes in a unified framework,we start with the QP equation, written in the Dirac′s notation,

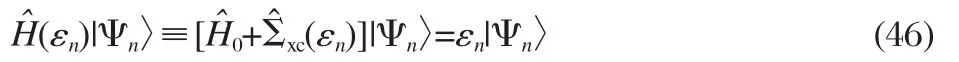
Now expand Ψnby a set of orthonormal single-particle wave functions｜φν〉,which are eigenfunctions of some single-particle effective Hamiltonian H^s

we then obtain the matrix form of Eq.(46)

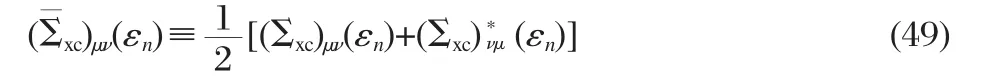
and in the meanwhile we neglect the imaginary part of the quasiparticle energies,i.e.,assuming εnto be all real.Due to the energy dependence of self-energy,Eq.(49)still can not be solved by standard linear algebra techniques.More importantly the QP wave functions at different energies are not orthogonal as a result of the energy dependence,which makes the construction of a self-consistent loop difficult.Different approximations are introduced to tackle this difficulty.

2.2.1 Faleev-van Schilfgaarde-Kotani scheme

In the so-called quasi-particle self-consistent GW(QSGW) scheme proposed by Faleev,van Schilfgaarde and Kotani (FvSK)[63-64],Eq.(48)is converted to an iterative equation by defining the effective Hamiltonianat i-th iteration as

2.2.2 Shishkin-Marsman-Kresse scheme

Shishkin,Marsman and Kresse(SMK)developed a slightly more sophisticated way to treat the energy dependence of the self-energy[24].The self-energyis first expanded around a reference energy

where the prime denotes the derivative with respect to the energy.After some simple algebraic transformations one obtains

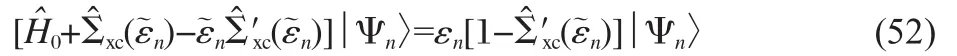
Using the expansion defined in Eq.(47),we then obtain the matrix form of Eq.(52)

where

A self-consistent loop can be constructed by choosing the reference energyfor i-th iteration,and further using the Hermitized form of Hμνand Sμνsimilarly as in the FvSK scheme (Eq.(50)).We note that the FvSK scheme can be recovered by dropping terms related toin Eq.(54).Since the contribution of the latter vanishes when reaching convergence as indicated by Eq.(51),we can see that the two schemes are actually equivalent.

2.2.3 Self-consistent COHSEX

An even simpler way to overcome the energy-dependence difficulty is to use Hedin′s static Coulomb hole and screened exchange(COHSEX)approximation[19-20].To see the underlying physical assumptions,the real part of the self-energy can be written down as

where Wc=W-ν andprepresents taking the Cauchy principle value.A static approximation to the self-energy is obtained by setting ω-εn=0 in Eq.(55)

The COHSEX self-energy is energy-independent and Hermitian, and therefore can be calculated in a self-consistent manner quite straightforwardly.The COHSEX itself tends to overestimate the band gaps of semiconductors,but one can use COHSEX orbital energies and wave-functions as the input for the full G0W0.This COHSEX based G0W0approach has been used by R.Reining and coworkers for Cu2O[23]and VO2[65]with remarkable success.

An approach closely related to the COHSEX approximation is the model GW approach first proposed by Gygi et al.[66],in which the self-energy correction with respect to the LDA exchangecorrelation potential is approximated by

where ρ(r,r′)is the density matrix function,and δW(r-r′)is a model function for the screened Coulomb interaction correction, whose Fourier transform takes the form

2.2.4 Sakuma-Miyake-Aryasetiawan scheme

Sakuma,Miyake and Aryasetiawan(SMA)proposed another approximate self-consistent GW scheme with some interesting new features[70].For a given set of single-particle orbitals,the quasi-particle energies and wave functions are calculated by solving Eq.(48)with the regularized self-energy Eq.(49)without introducing additional approximation to the energy-dependence. The price of this more rigorous treatment is that quasi-particle wave functions obtained in this manner are not orthogonal and therefore unsuitable as the input for the next iteration of calculations.SMA proposed to define the following effective quasi-particle Hamiltonian,

Using the corresponding eigen-energies and wavefuctions,one obtains a close loop to perform approximate SCGW calculations.

2.3 GW@LDA+U approach

The strategy underlying the G0W0approximation is that of“best G,best W”.The approximate SCGW schemes discussed above can be regarded as a generalization of this strategy,i.e., one tries to construct best G and W based on an effective singleparticle Hamiltonian that is as close to the full GW approximation as possible.In spite of substantial approximations already introduced in these schemes,the required computational efforts of these schemes are still very demanding.Considering that the problem of G0W0@LDA for d/f-electron systems originates first of all from that of the LDA,it is plausible to expect significant improvements by replacing LDA by some more accurate treatments.This is the basic idea underlying recent development of G0W0based on the optimized effective potential(OEP)exact exchange(EXX)[21],hybrid functionals[71]and LDA+U[25,72].Since the most efficient improvement of LDA for d/f-electron systems is the LDA+U method,we will focus on the G0W0@LDA+U method.

2.3.1 LDA+Umethod

For systems with partially occupied d or f shells,a simple and physically motivated approach that can correct the major failure of the LDA/GGA is to introduce a Hubbard-type local correction,characterized by the on-site Coulomb interaction U(the other parameter J that characterizes the on-site exchange interaction is less important and often absorbed into U in practice), hence termed LDA+U[8,73-74].The LDA+U total energy takes the form

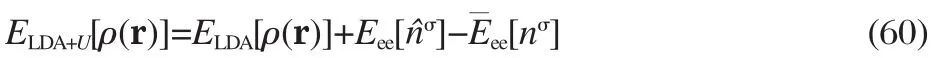
where σ=↑,↓,is the spin index,and to simplify the notation,we drop a and l,the indices for the atomic sites and local orbitals,to which the LDA+U correction is imposed.Eeeis the more“accurate”treatment of the interaction energy among localized electrons beyond LDA.is the mean-field interaction energy already included in LDA,and plays the role of double counting correction (DCC).As indicated explicitly,Eeeis a functional of on-site density matrices,and is usually treated in a Hartree-FocklikewayusingascreenedCoulombinteraction

Corresponding to the total energy in Eq.(60),the LDA+U single-particle Hamiltonian reads

2.3.2 LDA+Uas an approximation toGW

For highly localized d/f-states LDA+U can be viewed as an approximate GW scheme,as first pointed out by Anisimov et al.[8].Since the original derivation is fairly involved,we present here a simplified derivation starting from the COHSEX approximation[19-20]to the GW self-energy(the spin index is dropped for simplication).

Using the completeness relation

the COHSEX self-energy can be rewritten as

where fnis the occupation number(fn=1 for occupied states and fn=0 for unoccupied states).For d-or f-electron systems,we further assume that highly localized d or f-states,denoted as φm, are essentially separated from other itinerant states and the whole Hilbert space can be decomposed into two subsystems that are approximately orthogonal to each other.In the LDA+U approach only quasiparticle corrections δΣ for highly localized d/f-states are kept.This is equivalent to approximating δΣ by

where δΣxc≡Σxc-Vxcis restricted to the localized subspace.In the COHSEX approximation we have

If we neglect the anisotropic term of the Coulomb interaction and further assume the LDA electron-electron interaction energy can be approximated by a Hartree-Fock like expression(which is the same assumption made in the standard LDA+U formalism[8]),the last two terms in Eq.(68)will cancel each other.We then obtain

where U is identified as the spherically averaged screened Coulomb interaction matrix element[8].

To summarize,LDA+U can be regarded as an approximation to the GW approach under the assumptions that:

(1)the energy dependence of the screened Coulomb interaction is neglected;

(2)the quasiparticle corrections are only significant for the target localized states under study,and the LDA description is sufficient for itinerant states;

(3)the target localized states are well-separated from itinerant states,i.e.,the whole system can be partitioned into two subsystems that are coupled only by classical electrostatic interactions.

None of these assumptions are of course fulfilled in real systems.The dynamic character of the screened Coulomb interaction is actually stronger for localized electrons than for itinerant ones.The LDA description of the itinerant states suffers from the band gap problem and the coupling between localized and itinerant states is critical for the physical and chemical properties of d/f-electron systems.Since in virtually all LDA+U implementation thecorrection is applied to KS singleparticle states via a local projection,and the calculations are carried out self-consistently,δVUcan have an indirect effect on itinerant states as well.

2.3.3 The GW@LDA+Umethod

The preceding discussion elucidates that LDA+U is a rather crude approximation to GW and is therefore not expected to provide an accurate description of d or f-electron systems on its own.However,since LDA+U corrects the major failure of LDA for many d/f-electron systems,it would serve as a good starting point for G0W0calculations.Formally,the only difference between the LDA-and LDA+U-based G0W0formalism is the contribution of

The equation illustrates that the double-counting term contained in∈nkis exactly cancelled in the G0W0@LDA+U approach, which is a significant advantage of the scheme.Moreover,the explicit U dependence in Eq.(69)can actually be eliminated. The δcontribution in the LDA+U single-particle energies, denoted,can be split off

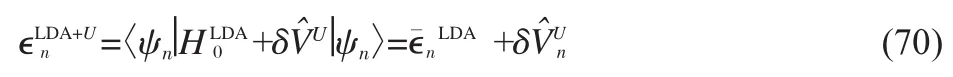
Eq.(71)has no explicit U-dependence,and the quasiparticle energies in G0W0@LDA+U therefore depend only implicitly on U.The two main factors are:1)the difference in wave functions between LDA+U and LDA,and 2)the change in screening introduced by the changes in the single-particle spectrum,most notably the band gap.Regarding point 1),occupied states with strong d/f-character will be pushed towards lower energies and become more localized as a result,whereas unoccupied states with strong d/f-character are pushed to higher energies and become more delocalized.This has a direct effect onin Eq. (71),because of the self-interaction error in LDA,which is larger for more localized states.The U-dependence of the second term in Eq.(71)is determined by the change in screening. Increasing U usually increases the band gap and therefore reduces screening.The limit of vanishing screening gives the Hartree-Fock self-energy,whose corresponding band gap is dramatically overestimated.The second term therefore has a tendency to increasetheG0W0@LDA+U bandgapwith increasing U.In practice both terms can significantly shape the U-dependence of the system under study.

3 GW method for d/f-electron systems:case studies

In this section we show a few examples in which GW is applied to prototypical d/f-electron systems.

3.1 NiO

Electronic properties of late 3d transition metal mono-oxides (TMOs),MnO,FeO,CoO and NiO,have been under intensive experimental and theoretical investigations for decades,and recently have attracted revived interest due to the fact that two classes of intriguing materials,high-temperature superconductors and colossal magneto-resistance materials are all closely related to these apparently very simple compounds.They are all anti-ferromagnetic insulators at T lower than Neel′s temperature and the nature of their band gaps have been under debate.Soon after the birth of the band theory,it was realized that the band theory,which achieved remarkable success for normal sp systems,would have serious difficulty when applied to systems with open d-orbitals,NiO in particular.Applying the band theory to late TMOs,which all take NaCl-type lattice structure, would inevitably lead to a metallic ground state,with the Fermi energy crossing the partially occupied d-states,which is in strong contrast to the insulating nature of these compounds found in expereiment.How to explain the origin of the insulating ground state of these materials has essentially led to two competing pictures of the transition metal oxides in particular,and all d/f-electron systems in general.In the Slater′s model,the band gap of NiO arises from the interplay between the crystal field splitting and the long-range anti-ferromagnetic ordering.Slater′s original argument would have difficulty to explain the fact that NiO maintains its insulating state even at T＞TN,i.e.,in the paramagnetic phase(PM),but it is formally possible to generalize the Slater′s model based on the observation that even in the PM phase,Ni atoms posses a local magnetic moment.On the other hand,the Mott-Hubbard model contends that the gap of NiO arises from the strong on-site Coulomb interaction,characterized by the Hubbard U.A material is metallic if it is energetically favourable for electrons to hop between sites,characterized the band width;when the on-site Coulomb interaction U becomes larger than the band width,it becomes energetically more favourable for electrons to stay localized on each site,therefore leading to an insulating ground state.

The two models may not be as incompatible as they appear.If we regard the long-range magnetic ordering as a special case of broken symmetry compared to the symmetric non-magnetic phase,it is possible to generalize the Slater′s model to incorporate any band splitting arising from the symmetry breaking of some kind.In this way,one will also include the Peierls transition(for 1D cases)and Jahn-Teller distortion(for more general cases)into this picture.The symmetry breaking in this generalized Slater picture makes the band theory compatible to the physics of strong on-site Coulomb interactions in the Mott-Hubbard model.Based on these notions,it is therefore fully justified to develop the band-theory-like approaches,to which the GW method belongs,for these d/f-electron systems.

Due to their structural simplicity,late TMOs have become the testbed for any newly developed first-principles approach that aims for going beyond the standard LDA/GGA approach[7,10,63,79-84]. The GW method has been applied to study the QP electronic structure of NiO by several authors[63,67-69,85-86].Aryasetiawan and Gunnarsson[79]applied the GW method implemented in the LMTO-ASA approach to NiO.It was found that the G0W0based on LDA only marginally increases the band gap of NiO from 0.2 eV to 1.0 eV,still dramatically underestimated compared to the experimental gap of ca 4 eV.By applying a non-local potential to egorbitals and updating G self-consistently,a gap of 5.5 eV was obtained,in reasonable agreement with experiment.It was also observed that the satellite structure at 8 eV binding energy can not be reproduced and the top of the valence band is still mainly dominated by the Ni d character,disagreeing with experiment.

Massidda et al.,used the model GW scheme discussed in the preceding section with full self-consistency to study electronic band structures of MnO[67]and NiO[68]and obtained band gaps in good agreement with experiment.Furthermore,they observed significantly enhanced O-2p character in top valence band states, in accord with the charge-transfer model of later transition metal oxides[90].These findings were confirmed by more recent GW studies[63,85-86,88].

Finally we compare density of states(DOS)of NiO obtained from different GW approaches to the experimental PES/IPS spectral data in Fig.5.One can see that in general different GW schemes give similar results.The band gap is most significantly overestimated in the QSGW approach.The DOS from the GW0@LDA+U agrees with experiment remarkably well.The sta-tellite structure at-8 eV is missing in all GW results.

3.2 Metallic and insulating phases of VO2

VO2is a prototype of strongly correlated transition metal oxides,and exhibits an intriguing metal-insulator(M-I)transition as the temperature is lowered across Tc=340 K,with a jump of the conductivity by nearly five orders of magnitude[91].What makes the physics of VO2complicated is that the M-I transition is accompanied by a structural change.The high-temperature metallic phase of VO2takes a tetragonal(rutile)structure,which, at the M-I transition,is distorted to a monoclinic one involving the dimerization of two neighbouring vanadium atoms.The nature of the VO2M-I transition has been under debate since 1960′s.Early work focused on two conflicting models.Goodenough interpreted the transition by a Peiers-like model,in which the gap opening is solely a consequence of the structural change(the dimerization)[92].Mott and co-workers,however,considered the transition of the Mott-Hubbard type,arising from strong on-site Coulomb interaction[93].In this Hubbard-Mott′s model,the pairing of vanadium atoms contributes only to destroying the anti-ferromagnetism that would be otherwise present,as in most Mott-Hubbard insulators.Recent experimental and theoretical studies seem to indicate that both the pairing and the on-site Coulomb interaction play an important role in the M-I transition of VO2[94-95].

Fig.5 Density of states of NiO from GW0@LDA+U(with U= 5.2 eV and J=0.8 eV as determined by the constrained DFT method)[87],G0W0@HSE03[88]and QSGW[64]compared to the experimental PES/IPS spectral data[89]

For theoretical studies,the LDA and single-site DMFT method predicts both phases to be metallic.On the other hand, the LDA+U predicts an insulating ground state even for the rutile phase.A recent cluster DMFT study reproduced the correct electronic state for both phases,indicating that inter-site electronic correlation plays a significant role.The metallic and insulating VO2have also been extensively studied by the GW method with different approximations.Using the model GW approach,Continenza et al.[69]obtained a correct band gap for the insulating phase,and the calculated density of states is also consistent with the PES data.Recently Gatti et al.[65]applied the G0W0@COHSEX approach to investigate the electronic properties of metallic and insulating VO2.The self-consistent COHSEX can already open a gap of 0.78 eV for the monoclinic VO2.The subsequent G0W0calculation reduces the gap slightly to 0.65 eV,in excellent agreement with experiment.For the metallic rutile phase,even the LDA DOS is already in good agreementwith experiment,and furtherGW corrections introduces only small changes.But the LDA can not describe the satellite structure observed in the experimental PES data at the binding energy of-1.3 eV.On the other hand,the loss function obtained from the GW calculations for the metallic phase exhibits a sharp peak at the-1.5 eV binding energy with a plasmon-like character.This interpretation of the satellite structure in the metallic VO2differs from the traditional picture in which the satellite is interpreted as the lower Hubbard band. Similar results were also obtained in another approximate selfconsistent GW study by Aryasetiawan and coworkers[70].

3.3 Lanthanide oxides

We have used the G0W0based on LDA+U to investigate electronic properties of CeO2and the whole series of lanthanide sesquioxides[25].These compounds have important technological applications[99-101],in particular in catalysis,where CeO2-based compounds have attracted considerable interest from both experiment and theory[96,98,102-107].It turns out that by using LDA+ U as the starting point,in which the Hubbard U correction is able to overcome the major failure of LDA to describe highly localized f-states,G0W0performs remarkably well for this class of materials.

Fig.6 shows the DOS of CeO2and Ce2O3calculated from LDA,LDA+U,and G0W0@LDA+U (with U=5.4 eV)together with the experimental spectra.In general,the G0W0DOS agrees well with the experimental data from direct(XPS)and inverse (BIS)photoemission spectroscopy or X-ray absorption spectroscopy(XAS).In CeO2,the empty f-states introduce a sharp peak in the fundamental band gap formed between the O-2p valence and Ce-5d conduction band.The G0W0predicts a p-d gap of 6.1 eV,in good agreement with the experimental one of 6.0 eV.The p-f gap,however,cannot be unambiguously determined from XPS-BIS or other available measurements(e.g.,Ref. [105]and references therein).As expected,LDA under estimates both gaps,but the p-d gap is only slightly smaller than in experiment(5.5 vs 6.0 eV),whereas LDA+U decreases it to 5.1 eV.In Ce2O3,the on-site Hubbard U splits the single f-peak in LDA to occupied and unoccupied f-bands(denoted as foccand fun, respectively),the former falling within the p-d gap and the latter overlapping with the conduction bands.The p-d gap is nearly the same as in LDA,but the p-foccsplitting is greatly reduced. The G0W0corrections based on the LDA+U push the O-2p band to lower energy with respect to the foccband,and in the meanwhile shift the funband in energy further away from the conduction band edge.By aligning the G0W0and the experimental spectrum in Fig.6 at the upper valence band edge,the funpeak in G0W0DOS is in good agreement with the BIS data,but the position of the foccpeak,however,differs by approximately 1 eV.

Fig.6 Density of states of CeO2(left)and Ce2O3(right)from LDA,LDA+U and G0W0@LDA+U with U=5.4 eV compared to experimental data(XPS+BIS and XPS+XAS)The XPS+BIS data for CeO2and Ce2O3has been extracted from Refs.[96]and[97],respectively,and the XPS+XAS data from Ref.[98].The Fermi energy (the valence band maximum for insulating states)is taken as zero.The small peak at ca 2 eV in the BIS curve of Ce2O3is probably due to the coexistence of the CeO2phase,as indicated in Fig.3 of Ref.[97].

In Fig.7 the optical gaps of the Ln2O3series are compared to LDA+U,G0W0@LDA+U and previous self-interaction corrected LDA(SIC-LDA)results[108].All the essential features in the experimental curve are well reproduced by the G0W0calculations including the four dips and the behaviour in between.Even the quantitative agreement is good for most compounds.In addition our first principles calculations provide easy access to the character of each peak in the DOS and thus the character of the band gap,which is schematically shown in the upper part of Fig. 7.In La2O3(empty f-shell)the band gap is formed between the O-2p valence and the La-5d conduction band.As the occupation of the f-states increases,both foccand funcontinuously move downward in energy and the band gap evolves from p-d via f-d to pf.This process repeats itself in the second part of the series (starting from Gd2O3)where the spin-up f-states have become fully occupied(and lie deep below the O-2p states)and the spindown f-states move downward in energy with increasing occupation.The character of the band gap across the series agrees well with the experimental conjecture derived from phenomenological arguments[109-111].This is not the case in SIC-LDA and LDA+U.Not only does LDA+U underestimate the band gaps of most Ln2O3compounds,it also only shows a weak minimum at Tb2O3and fails to reproduce the plateau between Ho2O3,Er2O3,and Tm2O3.

Fig.7 Band gaps of the Ln2O3series from LDA+U and G0W0 (U=5.4 eV)compared to SIC-LDA results[108]and experimental optical gaps[109]The schematic in the upper part of the figure illustrates the position of the foccand fun states extracted from the G0W0@LDA+U calculations in relation to the valence and conduction band edge(VB and CB).

4 Concluding remarks

The basic theoretical framework of Green′s function(GF) theory for real materials[19]was set up almost at the same time as the density functional theory,but compared to the tremendous popularity of the DFT methods nowadays,the GF methods remain to be highly specialized and limited to relatively simple systems.But the situations are changing quickly in recent years thanks to latest methodological developments and the rapid increase of computer power,and also to the stronger demand for accurate theoreticaldescriptions of electronic excitation properties.The latter becomes increasingly more important to tackle crucial scientific challenges that may have impact on the continual prosperity and survival of human civilization.For example,one of the most actively pursued scientific frontiers nowadays is to develop appropriate photo-catalytic or photovoltaic materials that can convert solar energy efficiently to chemical or electric energy,respectively.A rational design based on deep insights to underlying chemical and physical processes is critical to meet the technological challenge.The most critical parameters in these materials are the band gap,which determines the efficiency of solar energy absorption,and the relative energy level alignment of active molecular species with respect to the electrode materials.These properties are difficult to catch in the current DFT methods,but can be addressed directly by the GF methods.

There are still several crucial challenges to meet before it becomes feasible to employ the GF methods routinely for complicated real systems.The first challenge is how to improve the efficiency of the current GF methods so that it becomes feasible to routinely treat systems with tens or even hundreds of atoms.There have been already several interesting developments along this direction[112-113],but further efforts are still needed.In this aspect,we may borrow experiences from recent developments in linear scaling post-HF quantum chemistry methods[114-115].The second challenge is related to the accuracy of the current GF methods.As indicated in this work,even at the GW level,there are several additional approximations involved in practice.With recent proposal of several approximate selfconsistent GW schemes,it is still not clear what is the optimal way to perform GW calculations.The GW is just the first-order term in a many-body perturbation expansion with respect to W, which itself is an approximation with severe limitations,e.g.,its failure to describe the satellite structure in Ni and NiO.For many systems,in particular,open-shell d/f-electron systems, higher order contributions beyond GW are necessary even for a qualitatitive description.In some sense,what we need here is to set up a“Jacob′s ladder”for the GF methods,following Perdew′s idea for the DFT methods[116].Although the lowest level of the ladder is G0W0without doubt,it is still not clear what should be next levels.Finally,the current practice of the GF methods is a hybrid one,i.e.,the total energy is obtained from the DFT methods,and the GW method is used only to improve the quasi-particle energies.This is conceptually inconsistent and unnecessary since the Green′s function itself can be used to calculate the total energy directly.In practice,however,the GW total energy is computationally expensive to calculate.More importantly,it becomes almost necessary to perform full selfconsistent GW calculations to obtain accurate total energy.

Another equally important aspect of the GF theory is that it may provide useful insights for further development of the DFT and TDDFT.Both being many-body theories,the link between the GF theory and DFT has been noticed from the very beginning[117].While the GF theory often uses the ingredients of the DFT as first approximations,the concepts in the GF theory also play important roles in the developments of DFT and TDDFT. The early development of various LDA/GGA functionals owes a lot to the many-body theory treatment of homogeneous electron gas.Recently there has been a lot of interest of developing new exchange-correlation kernels based on the formal similarity between the TDDFT and the Bethe-Salpeter equation for optical excitation[17,18,118-121].New non-local frequency-dependent xc kernels have been proposed and applied to some simple systems with remarkable success[119-120].We can expect that more advance can be achieved by further fostering the close connection between the two theoretical frameworks.

1 Parr,R.G.;Yang,W.Density-functional theory of atoms and molecules.New York:Oxford University Press,1989

2 Dreizler,R.M.;Gross,E.K.U.Density functional theory:an approach to the quantum many-body problem.Berlin:Springer-Verlag,1990

3 Martin,R.M.Electronic structure.Cambridge,UK:Cambridge University Press,2004

4 Terakura,K.;Oguchi,T.;Williams,A.R.;Kübler,J.Phys.Rev. B,1984,30:4734

5 Anderson,P.W.Phys.Rev.,1961,124:41

6 Hubbard,J.Proc.Roy.Soc.(London),1963,A276:238

7 Anisimov,V.I.;Zaanen,J.;Andersen,O.K.Phys.Rev.B,1991, 44:943

8 Anisimov,V.I.;Aryasetiawan,F.;Lichtenstein,A.I.J.Phys.-Condes.Matter,1997,9:767

9 Perdew,J.P.;Zunger,A.Phys.Rev.B,1981,23:5048

10 Svane,A.;Gunnarsson,O.Phys.Rev.Lett.,1990,65:1148

11 Szotek,Z.;Temmerman,W.M.;Winter,H.Phys.Rev.B,1993, 47:4029

12 Becke,A.D.J.Chem.Phys.,1993,98:1372

13 Janesko,B.G.;Henderson,T.M.;Scuseria,G.E.Phys.Chem. Chem.Phys.,2009,11:443

14 Runge,E.;Gross,E.K.U.Phys.Rev.Lett.,1984,52:997

15 Time-dependent density functional theory.Lect.Notes.Phys.706. Marques,M.A.L.;Ullrich,C.A.;Nogueira,F.;Rubio,A.; Burke,K.;Gross,E.K.U.Eds.Berlin Heidelgerg:Springer,2006

16 Casida,M.E.J.Mol.Struct.-Theochem,2009,914:3

17 Onida,G.;Reining,L.;Rubio,A.Rev.Mod.Phys.,2002,74:601

18 Botti,S.;Schindlmayr,A.;Del Sole,R.;Reining,L.Rep.Prog. Phys.,2007,70:357

19 Hedin,L.Phys.Rev.A,1965,139:796

20 Aryasetiawan,F.;Gunnarsson,O.Rep.Prog.Phys.,1998,61: 237

21 Rinke,P.;Qteish,A.;Neugebauer,J.;Freysoldt,C.;Schefler,M. New.J.Phys.,2005,7:126

22 van Schilfgaarde,M.;Kotani,T.;Faleev,S.V.Phys.Rev.B, 2006,74:245125

23 Bruneval,F.;Vast,N.;Reining,L.Phys.Rev.B,2006,74: 045102

24 Shishkin,M.;Marsman,M.;Kresse,G.Phys.Rev.Lett.,2007, 99:246403

25 Jiang,H.;Gomez-Abal,R.;Rinke,P.;Scheffler,M.Phys.Rev. Lett.,2009,102:126403

26 Hedin,L.;Lundqvist,B.I.Solid State Phys.,1969,23:1

27 Inkson,J.C.Many-body theory of solids:an introduction.New York:Plenum,1983

28 Perdew,J.P.;Levy,M.Phys.Rev.Lett.,1983,51:1884

29 The density functional theory in the Kohn-Sham framework is a truly many-body theory as far as the ground state total energy is concerned;but Kohn-Sham single-particle Hamiltonian is of mean-field nature.

30 Sham,L.J.;Schlüter,M.Phys.Rev.Lett.,1983,51:1888

31 Godby,R.W.;Schlüter,M.;Sham,L.J.Phys.Rev.B,1988,37: 10159

32 Städele,M.;Majewski,J.A.;Vogl,P.;Görling,A.Phys.Rev. Lett.,1997,79:2089

33 Niquet,Y.M.;Gonze,X.Phys.Rev.B,2004,70:245115

34 Grüning,M.;Marini,A.;Rubio,A.J.Chem.Phys.,2006,124: 154108

35 Engel,E.;Schmid,R.N.Phys.Rev.Lett.,2009,103:036404

36 Kümmel,S.;Kronik,L.Rev.Mod.Phys.,2008,80:3

37 Kotani,T.J.Phys.-Condes.Matter,1998,10:9241

38 Hellgren,M.;von Barth,U.Phys.Rev.B,2007,76:075107

39 Cohen,A.J.;Mori-Sanchez,P.;Yang,W.Phys.Rev.B,2008, 77:115123

40 Fetter,A.L.;Walecka,J.D.Quantum theory of many-particle systems.New York:McGraw-Hill,1971

41 Arfken,G.B.;Weber,H.J.Mathematical methods for physicists. 5th ed.San Diego:Academic Press,2001

42 Linderberg,J.;Öhrn.Y.Propagators in quantum chemistry.2nd ed.Hoboken,New Jersey:John Wiley&Sons,2004

43 Blaha,P.;Schwarz,K.;Madsen,G.K.H.;Kvasnicka,D.;Luitz,J. WIEN2k,an augmented plane wave+local orbitals program for calculating crystal properties.Techn.Universitat Wien,Austria, 2001

44 Gomez-Abal,R.;Li,X.;Scheffler,M.;Ambrosch-Draxl,C.Phys. Rev.Lett.,2008,101:106404

45 Bylander,D.M.;Kleinman,L.Phys.Rev.B,1990,41:7868

46 Heyd,J.;Scuseria,G.E.;Ernzerhof,M.J.Chem.Phys.,2003, 118:8207

47 Lee,B.;Wang,L.W.;Spataru,C.D.;Louie,S.G.Phys.Rev.B, 2007,76:245114

48 Garcia-Lastra,J.M.;Rostgaard,C.;Rubio,A.;Thygesen,K.S. Phys.Rev.B,2009,80:245427

49 Shishkin,M.;Kresse,G.Phys.Rev.B,2007,75:235102

50 Hybertsen,M.S.;Louie,S.G.Phys.Rev.B,1986,34:5390

51 Godby,R.W.;Schlüter,M.;Sham,L.J.Phys.Rev.B,1987,36: 6497

52 Ku,W.;Eguiluz,A.G.Phys.Rev.Lett.,2002,89:126401

53 Tiago,M.L.;Ismail-Beigi,S.;Louie,S.G.Phys.Rev.B,2004, 69:125212

54 Baym,G.;Kadanoff,L.P.Phys.Rev.,1961,124:287

55 Baym,G.Phys.Rev.,1962,127:1391

56 de Groot,H.J.;Bobbert,P.A.;van Haeringen,W.Phys.Rev.B, 1995,52:11000

57 von Barth,U.;Holm,B.Phys.Rev.B,1996,54:8411

58 Shirley,E.L.Phys.Rev.B,1996,54:7758

59 Holm,B.;von Barth,U.Phys.Rev.B,1998,57:2108

60 Schöne,W.D.;Eguiluz,A.G.Phys.Rev.Lett.,1998,81:1662

61 Kutepov,A.;Savrasov,Y.;Kotliar,G.Phys.Rev.B,2009,80: 041103(R)

62 Zein,N.E.;Savrasov,S.Y.;Kotliar,G.Phys.Rev.Lett.,2006, 96:226403

63 Faleev,S.V.;van Schilfgaarde,M.;Kotani,T.Phys.Rev.Lett., 2004,93:12640

64 Kotani,T.;van Schilfgaarde,M.;Faleev,S.V.Phys.Rev.B, 2007,76:165106

65 Gatti,M.;Bruneval,F.;Olevano,V.;Reining,L.Phys.Rev.Lett., 2007,99:266402

66 Gygi,F.;Baldereschi,A.Phys.Rev.Lett.,1989,62:2160

67 Massidda,S.;Continenza,A.;Posternak,M.;Baldereschi,A. Phys.Rev.Lett.,1995,74:2323

68 Massidda,S.;Continenza,A.;Posternak,M.;Baldereschi,A. Phys.Rev.B,1997,55:13494

69 Continenza,A.;Massidda,S.;Posternak,M.Phys.Rev.B,1999, 60:15699

70 Sakuma,R.;Miyake,T.;Aryasetiawan,F.Phys.Rev.B,2008, 78:075106

71 Fuchs,F.;Furthmüller,J.;Bechstedt,F.;Shishkin,M.;Kresse,G. Phys.Rev.B,2007,76:115109

72 Miyake,T.;Zhang,P.;Cohen,M.L.;Louie,S.G.Phys.Rev.B, 2006,74:245213

73 Anisimov,V.I.;Gunnarsson,O.Phys.Rev.B,1991,43:7570

74 Anisimov,V.I.;Solovyev,I.V.;Korotin,M.A.;Czyzyk,M.T.; Sawatzky,G.A.Phys.Rev.B,1993,48:16929

75 Liechtenstein,A.I.;Anisimov,V.I.;Zaanen,J.Phys.Rev.B, 1995,52:R5467

76 Czyzyk,M.T.;Sawatzky,G.A.Phys.Rev.B,1994,49:14211

77 Dudarev,S.L.;Botton,G.A.;Savrasov,S.Y.;Humphreys,C.J.; Sutton,A.P.Phys.Rev.B,1998,57:1505

78 Petukhov,A.G.;Mazin,I.I.;Chioncel,L.;Lichtenstein,A.I. Phys.Rev.B,2003,67:153106

79 Aryasetiawan,F.;Gunnarsson,O.Phys.Rev.Lett.,1995,74: 3221

80 Tran,F.;Blaha,P.;Schwarz,K.;Novak,P.Phys.Rev.B,2006, 74:155108

81 Kunes,J.;Anisimov,V.I.;Skornyakov,S.L.;Lukoyanov,A.V.; Vollhardt,D.Phys.Rev.Lett.,2007,99:156404

82 Kobayashi,S.;Nohara,Y.;Yamamoto,S.;Fujiwara,T.Phys.Rev. B,2008,78:155112

83 Rödl,C.;Fuchs,F.;Furthmüller,J.;Bechstedt,F.Phys.Rev.B, 2008,77:184408

84 Sharma,S.;Dewhurst,J.K.;Lathiotakis,N.N.;Gross,E.K.U. Phys.Rev.B,2008,78:201103(R)

85 Li,J.L.;Rignanese,G.M.;Louie,S.G.Phys.Rev.B,2005,71: 193102

86 Patterson,C.H.Int.J.Quantum Chem.,2006,106:3383

87 Jiang,H.;Gomez-Abal,R.I.;Rinke,P.;Scheffler,M.in preparation

88 Rödl,C.;Furthmüller,J.;Bechstedt,F.Phys.Rev.B,2009,79: 235114

89 Sawatzky,G.A.;Allen,J.W.Phys.Rev.Lett.,1984,53:2339

90 Zaanen,J.;Sawatzky,G.A.;Allen,J.W.Phys.Rev.Lett.,1985, 55:418

91 Mott,N.F.Metal-insulator transitions.2nd ed.London:Taylor& Francis,1990

92 Goodenough,J.B.Phys.Rev.,1960,117:1442

93 Zylbersztejn,A.;Mott,N.F.Phys.Rev.B,1975,11:4383

94 Biermann,S.;Poteryaev,A.;Lichtenstein,A.I.;Georges,A. Phys.Rev.Lett.,2005,94:026404

95 Haverkort,M.W.;Hu,Z.;Tanaka,A.;Reichelt,W.;Streltsov,S. V.;Korotin,M.A.;Anisimov,V.I.;Hsieh,H.H.;Lin,H.J.; Chen,C.T.;Khomskii,D.I.;Tjeng,L.H.Phys.Rev.Lett.,2005, 95:196404

96 Wuilloud,E.;Delley,B.;Schneider,W.-D.;Baer,Y.Phys.Rev. Lett.,1984,53:202

97 Allen,J.W.J.Magn.Magn.Mater.,1985,47-48:168

98 Mullins,D.R.;Overbury,S.H.;Huntley,D.R.Surf.Sci.,1998, 409:307

99 Adachi,G.;Imanaka,N.Chem.Rev.,1998,98:1479

100 Trovarelli,A.Catalysis by ceria and related materials.London: Imperial College Press,2002

101 Rare earth oxides thin films.Vol.106 of Topics in Appl.Phys. Fanciulli,M.;Scarel,G.Eds.Berlin Heidelberg:Springer-Verlag, 2007

102 Marabelli,F.;Wachter,P.Phys.Rev.B,1987,36:1238

103 Skorodumova,N.V.;Ahuja,R.;Simak,S.I.;Abrikosov,I.A.; Johansson,B.;Lundqvist,B.I.Phys.Rev.B,2001,64:115108

104 Silva,J.L.F.D.;Ganduglia-Pirovano,M.V.;Sauer,J.;Bayer,V.; Kresse,G.Phys.Rev.B,2007,75:045121

105 Castleton,C.W.M.;Kullgren,J.;Hermansson,K.J.Chem.Phys., 2007,127:244704

106 Fabris,S.;de Gironcoli,S.;Baroni,S.;Vicario,G.;Balducci,G. Phys.Rev.B,2005,71:041102(R)

107 Pourovskii,L.V.;Amadon,B.;Biermann,S.;Georges,A.Phys. Rev.B,2007,76:235101

108 Petit,L.;Svane,A.;Szotek,Z.;Temmerman,W.M.Phys.Rev. B,2005,72:205118

109 Prokofıev,A.V.;Shelykh,A.I.;Melekh,B.T.J.Alloy.Compd, 1996,242:41

110 Lal,H.B.;Gaur,K.J.Mater.Sci.,1988,23:919

111 van der Kolk,E.;Dorenbos,P.Chem.Mater.,2006,18:3458

112 Caramella,L.;Onida,G.;Finocchi,F.;Reining,L.;Sottile,F. Phys.Rev.B,2007,75:205405

113 Umari,P.;Stenuit,G.;Baroni,S.Phys.Rev.B,2009,79:201104 (R)

114 Schütz,M.;Hetzer,G.;Werner,H.J.J.Chem.Phys.,1999,111: 5691

115 Ayala,P.Y.;Scuseria,G.E.J.Chem.Phys.,1999,110:3660

116 Perdew,J.P.;Schmidt,K.AIP Conf.Proc.,2001,577:1

117 Sham,L.J.;Kohn,W.Phys.Rev.,1966,145:561

118 Reining,L.;Olevano,V.;Rubio,A.;Onida,G.Phys.Rev.Lett., 2002,88:066404

119 Sottile,F.;Olevano,V.;Reining,L.Phys.Rev.Lett.,2003,91: 056402

120 Marini,A.;Del Sole,R.;Rubio,A.Phys.Rev.Lett.,2003,91: 256402

121 von Barth,U.;Dahlen,N.E.;van Leeuwen,R.;Stefanucci,G. Phys.Rev.B,2005,72:235109

November 30,2009;Revised:January 19,2010;Published on Web:February 23,2010.

The GW Method:Basic Principles,Latest Developments and Its Applications for d-and f-Electron Systems

JIANG Hong*
(Beijing National Laboratory for Molecular Sciences,National Laboratory of Rare Earth Material Chemistry and Application,Institute of Theoretical and Computational Chemistry,College of Chemistry and Molecular Engineering,Peking University,Beijing 100871,P.R.China)

The many-body perturbation theory based on the Green′s function provides a rigorous conceptual framework to describe ground-state and excited-state properties of materials.The Green′s function depends on the exchange-correlation self-energy,which is the solution of a set of complicated integro-differential equations,named Hedin′s equations.The method,which approximates the self-energy by its first-order term in terms of the screened Coulomb interaction(W),is currently the most accurate first-principles approach to describe quasi-particle electronic band structure properties of extended systems.In this review,we first give an overview of the many-body perturbation theory for quasi-particle excitations based on the Green′s function and screened Coulomb interaction.The latest methodological developments are reviewed with an attempt to put different newly proposed schemes in a unified framework.The current status of the method,in particular for d/f-electron systems,is illustrated by a few prototypical examples.

Many-body perturbation theory; GW approximation; Quasi-particle electronic band structure; d/f-electron systems; Strongly correlated electron system

I wish to acknowledge Dr.Ricardo I. Gomez-Abal,Dr.Patrick Rinke and Professor Matthias Scheffler for the fruitful collaborations during my stay at Fritz-Haber Insitut-der-MPG as a postdoc.I also thank Professor E.K.U. Gross,Dr.Xinguo Ren and Dr.Xinzheng Li for stimulating discussions.

*Corresponding author.Email:h.jiang@pku.edu.cn;Tel:+86-10-62765970

O641