一种基于2DOF H∞控制器的航天器姿态控制方法

梁红义，张锦江

(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京 100190)

一种基于2DOFH∞控制器的航天器姿态控制方法

梁红义1,2，张锦江1,2

(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京100190)

研究某航天器俯仰轴姿态的二自由度鲁棒控制问题.首先分析俯仰轴系统中存在的主要不确定性，建立系统的结构与非结构不确定模型；然后将二自由度鲁棒控制方法应用于俯仰轴系统中设计H∞控制器，由于得到的H∞控制器阶次过高，对其进行降阶处理；最后进行仿真验证.结果表明该控制器对干扰力矩和参数不确定性的影响具有良好的鲁棒稳定性.

二自由度鲁棒控制；H∞控制；航天器姿态控制；鲁棒稳定性

大型空间结构航天器在轨运行时，受到未建模动态、模型参数不确定性和外部干扰力矩的影响.特别是航天器的挠性结构部分建模存在振动未知、理论计算参数与在轨运行实际数据有偏差等情况，使得大型空间结构航天器的建模及控制器设计相对困难和复杂.

现代鲁棒控制理论的研究始于1975年，目前已得到广泛应用，取得了不错的控制效果[1].其中以H∞控制方法应用最多，它以输出灵敏度函数的H∞范数作为性能指标，旨在可能发生“最坏扰动”的情况下，使系统的误差在无穷范数意义下达到极小，从而将干扰问题转化为求解使闭环系统稳定，并使相应的H∞范数指标极小化的输出反馈控制器问题[2].

关于挠性航天器鲁棒控制技术研究工作早在90年代就开始了，文献[3-4]综述了鲁棒方法在挠性卫星上的应用，并进行了物理仿真研究，但研究对象过于简单，挠性模态考虑不满足完备性要求，文献[5]针对挠性卫星进行单自由度鲁棒控制器设计又偏保守，没有考虑控制力矩输出要求，控制效果不甚理想.

本文在建模时考虑实际航天器参数，使用有限元方法分析挠性体模态满足惯性完备性要求，应用现代鲁棒控制理论的研究成果[6-7]，采用两自由度的鲁棒优化控制方法，设计了使某航天器俯仰轴姿态稳定且具有良好抗干扰能力的H∞控制器，最后对所设计的控制系统进行了仿真研究，仿真结果验证了闭环系统具有良好的鲁棒稳定性.

1 俯仰轴系统模型及不确定性分析处理

本文采用传统的中心刚体加两块挠性帆板模型建立系统的动力学方程，其中线性化以后俯仰通道的动力学方程[8]为：

式(1)为系统绕质心的转动方程，式(2)和(3)为左右两块帆板的挠性模态坐标方程.Iy是航天器俯仰轴的转动惯量；θ为俯仰角；Uy,Tdy分别表示控制力矩和干扰力矩；η∈Rm×1,ξ和Ω=diag{λ1,λ2，…,λm}分别为挠性模态的模态坐标、阻尼系数(一般取0.005)和模态频率对角阵，m是模态坐标的截断数，这里分左右两块帆板两组参数；Fly,Fry∈R1×m分别为左右两挠性帆板振动与中心体转动的耦合系数阵.

联立式(1)、(2)和(3)得：

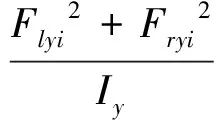
图1 俯仰轴传递函数方框图

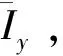
式中，pIy代表转动惯量的变化比例，δIy∈[-1,1].

经过线性分式变换(LFT)得：

挠性模态坐标方程中，挠性模态频率阵Ω和耦合系数阵Fly,Fry由有限元分析得到，与实际在轨运行参数存在误差，而取前m阶模态坐标进行建模本身就存在模型截断误差.

对于挠性模态方程中的参数不确定和模型截断误差，H∞控制中将其看作乘性摄动处理[9]，其系统模型如图2所示.

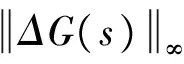
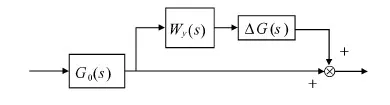
图2 乘法不确定性

Wy(s)表示ΔG(s)的摄动界函数，也称加权函数.给出挠性结构在原频带±10%范围内的幅频特性，设计Wy(s)覆盖它们，而且尽量靠近实际摄动，以降低模型保守性.

2 两自由度H∞控制器设计

两自由度控制的思想就是通过将参考输入直接前馈到控制输入端来加快信号的跟踪响应，这时的控制器满足[10-11]：

用一个反馈控制器K2作用于系统以取得系统内部稳定性.另外在参考输入的前向通道上设计控制器K1使系统满足跟踪性、鲁棒稳定性和干扰抑制性要求(如图3所示).其中M(s)为系统设计时期望的闭环系统模型.

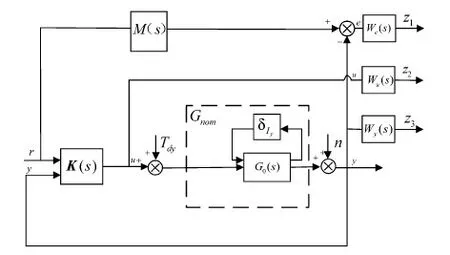
图3 2DOF控制流程图

图3所示系统设计中引入了一组评价信号为Z=(z1,z2,z3)T，We,Wu,Wy分别表示性能加权函数、控制量加权函数和输出加权函数.从图中很容易得到从系统输入(r,Tdy,n)T到Z=(z1,z2,z3)T的传递函数Tzw(s).

此外，H∞控制设计的一个缺点就是得到的控制器阶次过高，这样的控制器在工程实现上不满足简单可靠的要求，所以需要对控制器进行模型降阶处理.目前广泛应用的方法有内部平衡截断法、Hankel-范数近似法[12]等.

3 数值实例

以某航天器数据为例，选取燃料消耗一半时系统为标称系统模型，此时系统的转动惯量为：Iy=7.0718×104kg·m2，航天器在燃料全满和燃料耗尽时分别代表摄动的上下界，简单起见，统一取摄动在±20%内变化.挠性振动模态截断数m=6(高阶挠性的振动模态按系统未建模动态考虑)，建立标称系统模型G0.

不确定系统模型和标称系统模型的频域响应曲线见图4.

从图4中可以看出除了某些频率区域的扰动外，标称系统模型和不确定系统的频率特性是相符的，可以使用标称系统代替不确定系统来进行系统控制器的设计.

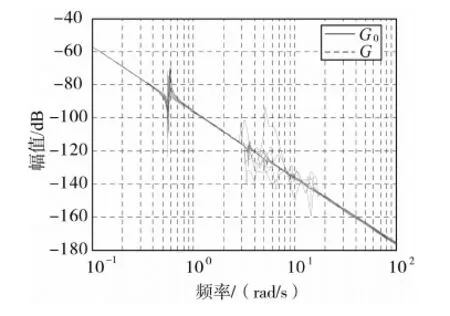
图4 不确定系统和标称系统的频域响应曲线

H∞控制中加权函数的选择尤为重要，选取遵照一定的规则[13-14]并经过不断调整，本文选取：

使用Matlab里的H∞最优控制器，求得的控制器为32阶.闭环系统的奇异值曲线见图5.

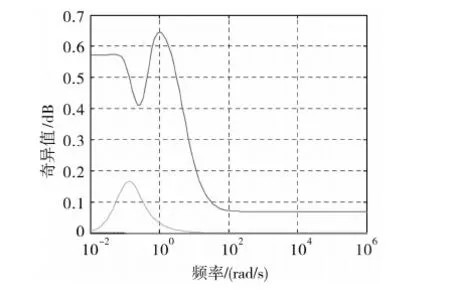
图5 闭环系统奇异值曲线

从图5可以看出

说明满足标准H∞控制设计要求.

本文使用Hankel-范数近似法[12]进行控制器模型降阶，得到一个9阶的控制器：

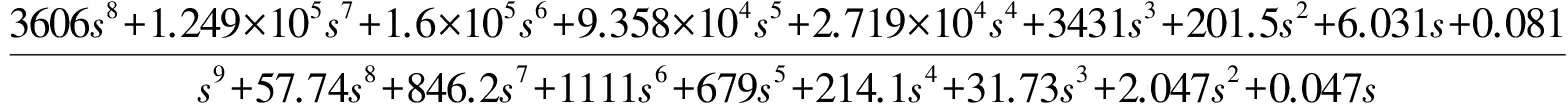
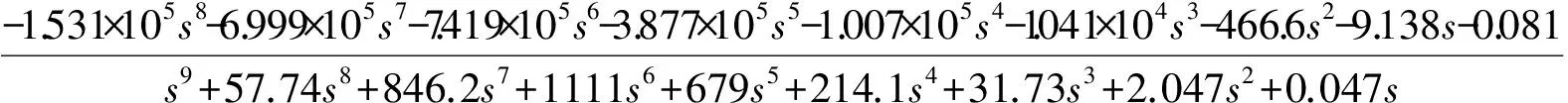
对闭环系统进行仿真，干扰力矩主要包括重力梯度力矩、气动力矩和磁力矩，经推算三种干扰力矩的最大干扰值之和为0.419N·m，它们主要影响航天器在轨道周期内的角动量积累，取

Tdy=[0.5+0.5sin(ω0t)+0.5cos(ω0t)],

其中ω0=1.119×10-3rad/s是航天器轨道角速度.姿态初始角为5°，姿态敏感器的量测噪声取为高斯白噪声.由于航天器的姿态控制基本上是由控制力矩陀螺(CMG)来完成，目前我们使用的CMG输出的最大控制力矩是20N·m，所以仿真时控制力矩输出加入±20N·m的限幅.

与传统的PID控制结果进行分析比较，依据稳定性和快速性的设计要求，取传统的PID参数:KP=266.89；KI=0.14；KD=7.529×103，仿真结果如图6～7所示.

（3）当地村民小农思想较为严重，不愿意进行土地流转，愿意进行土地流转的村民也由于当地土地质次、盐碱化严重，很难吸收到大型涉农企业进行投资，所以集约化种植也较为困难。

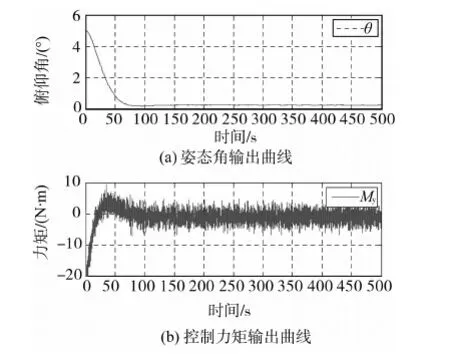
图6 PID控制的姿态角输出和控制力矩输出曲线

从图6中看出传统的PID控制器在应对参数摄动和干扰力矩影响时，系统虽然能稳定但达到稳态时有0.18°的静差，虽然可以通过增大积分系数来消除，但同时却增加了系统的超调量，不可取.同时控制力矩受噪声影响很大，工程上不可实现，且CMG长期处于饱和工作状态.

从图 7可以看出PID控制对挠性模态的振动抑制作用很小，挠性模态坐标在400s以后才有较大衰减.

从图8中看出H∞控制器在参数摄动和干扰力矩作用下，系统仍能稳定；控制力矩受噪声影响很小，工程上可以实现，其力矩输出在幅值要求范围内.

图7 PID控制的挠性模态坐标输出曲线

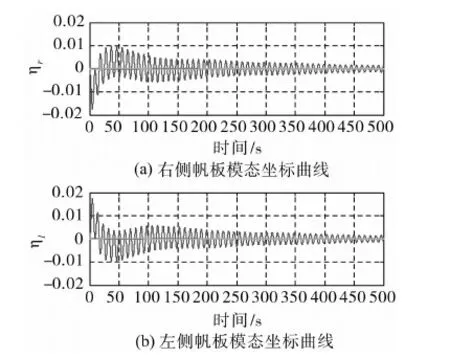
图9 H∞控制的挠性模态坐标输出曲线

图9清楚表明，H∞控制器对挠性模态振动有明显的抑制作用，挠性模态坐标在200s以后就有较大衰减，500s时衰减已经接近为0.

为了更清楚地说明H∞控制器对参数摄动和干扰力矩影响的抑制作用，姿态初始角取为0°，其他条件不变，仿真结果如图10～11所示.

图10 H∞控制的姿态角输出和控制力矩输出曲线

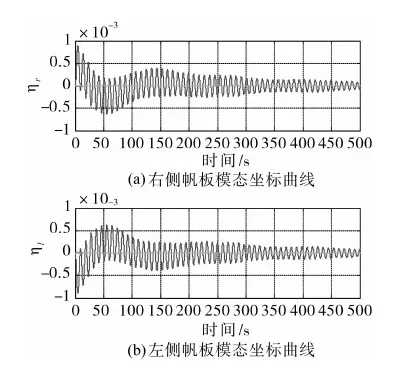
图11 H∞控制的挠性模态坐标输出曲线

4 结 论

对于既含参数不确定性又含未建模动态的航天器姿态控制系统，本文给出了一种两自由度H∞控制设计方法，按照这种方法设计的H∞控制器，可以保证使航天器俯仰轴姿态内稳定且具有良好抗干扰性能和鲁棒性能.文中给出的仿真实例说明了该方法的有效性.

[1] Zhou K，Doyle J C，Glover K.Robust and optimal control [M].Upper Saddle River, New Jersey: Prentice-Hall, 1996

[2] 阮洪宁，史忠科，吴方向，王蓓.鲁棒控制理论[M].北京: 国防工业出版社，2003

[3] 陈亚陵.挠性卫星姿态运动的鲁棒控制技术[J].厦门大学学报, 2001, 40(2): 211-219

[4] Zhi H Y, Guang F M,Chuan J L.Robust control synthesis method for the satellite [C].International Conference on Machine Learning and Cybernetics, Xi’an, China, Nov.2-5, 2003

[5] 宋斌,马广富,李传江,谌颖.基于H∞鲁棒控制的挠性卫星姿态控制[J].系统仿真学报, 2005, 17(4):968-970

[6] Fialho I J，Bushnell G S，Allen J L, Quraishi N.TakingH∞to the international space station : design，implementation and on-orbit evaluation of robust controllers for active microgravity isolation[C].AIAA Guidance, Navigation, and Control Conference and Exhibit，Austin, Texas，2003

[7] Chiang R Y，Liu J Y，Bender D J.Integrated robust control design methodology for an advanced spacecraft with large flexible structure[C].AIAA Guidance, Navigation and Control Conference and Exhibit.Honolulu, Hawaii，2008

[8] 章仁为.卫星轨道姿态动力学与控制[M].北京: 北京航空航天大学出版社，1997

[9] 梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用[M].北京: 清华大学出版社，2002

[10] Dehghani A, Lanzon A, and Anderson B .AnH∞model referencing design utilizing a two degree of freedom controller scheme[C].The 44thIEEE Conference on Decision and Control, and the European Control Conference，Seville, Spain，2005

[11] Hoyle D J, Hyde R A, Limebeer D J N.AnH∞approach to two-degree-of-freedom design[C].The 30thIEEE Conference on Decision and Control，Brighton, UK，1991

[12] Doyle G, Balas J, John C.Robust control toolbox user’s guide [Z].Version 3 the Math Works Inc, 2001

[13] 解学书，吴旭东.H∞鲁棒控制中的加权阵选择[J].清华大学学报，1997,37(1)：27-30

[14] Cerone V, Milanese M, Regruto D.Yaw stablity control design through a mixed sensitivity approach [C].IEEE Intelligent Vehicles Symposium, Istanbul, Turkey, 2007

A2DOFH∞Controller-BasedAttitudeControlDesignApproachforaSpacecraft

LIANG Hongyi1,2, ZHANG Jinjiang1,2

(1.BeijingInstituteofControlEngineering,Beijing100190，China;2.NationalKeyLaboratoryofScienceandTechnologyonSpaceIntelligentControl,Beijing100190,China)

This paper presents a 2DOF (two-degree-of-freedom)H∞controller based pitch-axis attitude control design approach for a spacecraft.A dynamics model of pitch-axis attitude control system with structured and unstructured uncertainties is analyzed and established.Then theH∞controller is designed by using the two-degree-of-freedom robust control approach.Because the order of the controller is very high, the Hankel-norm approximation is used to reduce the order of the controller.Finally, Simulations demonstrate that thisH∞controller has better robust stability to influences of disturbance torques and parameter uncertainties.

two-degree-of-freedom robust control;H∞control; spacecraft attitude control; robust stability

2009-12-18

梁红义(1983—), 男，河南人，硕士研究生，研究方向为航天器智能控制 (e-mail: lian2116@163.com).

V448.2

A

1674-1579(2010)02-0042-05