基于小波变换和2DPCA的人脸识别
翟俊海,翟梦尧,王华超
(河北大学数学与计算机学院河北省机器学习与计算智能重点实验室,河北保定 071002)
基于小波变换和2DPCA的人脸识别
翟俊海,翟梦尧,王华超
(河北大学数学与计算机学院河北省机器学习与计算智能重点实验室,河北保定 071002)
主成分分析(p rincipal component analysis:PCA)已成功用于人脸识别,但基于主成分分析的人脸识别方法需要将图像数据向量化,而向量化后的图像样本维数非常大,计算代价非常高.二维主成分分析(2 dimension p rincipal component analysis:2DPCA)直接处理图像数据,不需要向量化的过程,2DPCA降低了计算复杂度,但是2DPCA与PCA相比,需要存储更多的系数,即要占用更多的存储空间.本文提出了一种基于小波变换和2DPCA的人脸识别方法,可以克服上述缺点,实验结果证明了该方法的有效性.
小波变换;人脸识别;主成分分析;特征脸;特征提取
计算机自动人脸识别就是以计算机作为辅助工具,利用存储在数据库中的人脸图像,从给定场景的静止或视频图像中识别1个或多个人[1].人脸识别方法大致可分为基于模板的方法和基于特征的方法2大类.基于模板的人脸识别方法中,代表性的工作包括Turk等[2]提出的基于主成分分析的特征脸方法,Belhumeur等[3]提出的基于线性判别分析的费舍尔特征脸方法和Bartlett等[4]提出的基于独立成分分析的人脸识别方法等.基于特征的方法中,代表性的工作包括Wiskott等[5]提出的图匹配方法,Samaria等[6]提出的隐马尔科夫模型方法和Law rence等[7]提出的卷积神经网络方法等.基于PCA的人脸识别方法,需要将图像矩阵数据向量化,而向量化后的图像样本数据维数非常高,如一幅大小为256×256的图像,向量化后的样本维数为65 536,这么高维的数据学习容易产生小样本问题,即样本特征的维数比样本数高很多,从而导致协方差矩阵的奇异性问题.另外,高维的数据学习所需的计算代价非常大.为了克服上述缺点,Yang等[8]提出了二维主成分分析(2DPCA),2DPCA直接处理图像矩阵数据,不需要图像向量化的过程,降低了计算复杂度.但2DPCA与PCA相比,需要存储更多的系数,即要占用更多的存储空间[9].例如,若图像的分辨率为112× 92,则需要存储112×d个系数,其中,d是选择的投影方向数,一般要求d≥5.这对于髙维图像,其计算复杂度依然很高.本文提出了一种基于小波变换和2DPCA的人脸识别方法,该方法充分利用小波变换具有降2采样和快速计算的特点,该方法可以克服上述缺点,实验结果证明了该方法的有效性.
1 小波变换与二维主成分分析
本节简要介绍将要用到的一些基本概念和定义,主要包括小波变换[10]和二维主成分分析.
1.1 小波变换
设f(x,y)是大小为M×N的图像,则f(x,y)的离散小波变换可表示为


图1 图像的小波分解示意Fig.1 Flowchart of image wavelet decom position
f(x,y)的小波变换包括沿水平方向(x轴方向)和垂直方向(y轴方向)的滤波和降2采样2步构成.沿水平方向(x轴方向)的低通滤波是通过具有脉冲响应l(n)的低通滤波器L实现的,而高通滤波是通过具有脉冲响应h(n)的高通滤波器H实现的.沿垂直方向(y轴方向)的滤波和沿水平方向的滤波类似,如图1所示.其中,fLL表示沿水平和垂直2个方向的低频成分;fHL表示水平方向的高频成分和垂直方向的低频成分;
fLH表示水平方向的低频成分和垂直方向的高频成分;fHH表示沿水平和垂直2个方向的高频成分.对1层小波分解得到的低频子图f(1)LL重复进行小波变换可得2层小波分解.
1.2 二维主成分分析
2DPCA是经典PCA的推广,克服了PCA处理二维数据需要向量化的缺点.它直接从图像数据构造图像协方差矩阵Gt,并计算d个最佳投影方向X1,X2,…,Xd,使得

可用2DPCA的d个投影方向X1,X2,…,Xd来提取图像A的特征,令Yk=A Xk,k=1,2,…,d,则d个投影特征向量Y1,Y2,…,Yd构成一个投影特征矩阵B={Y1,Y2,…,Yd}.
2 基于小波变换和2DPCA的人脸识别方法
2.1 小波子段图像的选取
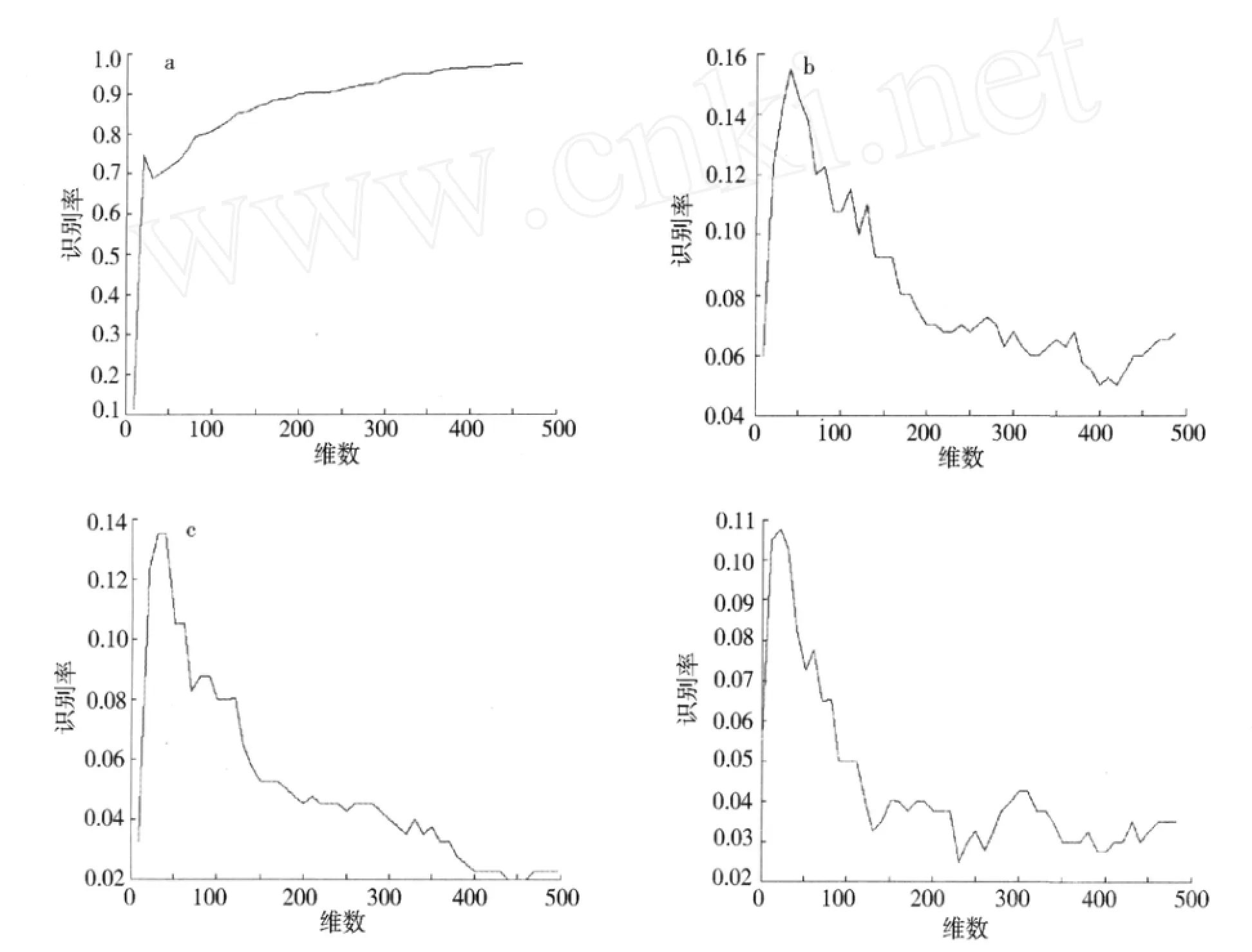
图2 4个小波子段图像作为训练样本的识别结果Fig.2 Resultsof face recognition with 4 different wavelet sub-band images
图像小波变换是一个1变4的过程,这4个子段图像,对于人脸识别任务来说,哪个子段图像更具表示能力呢?目前,理论上还没有统一的结论,笔者用实验的方法进行了分析.以ORL人脸图像数据库为例,对图像数据库中的每1幅人脸图像,做1次小波分解,得到4个子段图像f(1)LL,f(1)HL,f(1)LH,f(1)HH.然后,以每个子段图像替代原图像作为训练样本,并用PCA方法进行特征提取,用最近邻分类器进行人脸识别.结果如图2所示.从实验结果来看,对人脸识别来说,人脸的主要特征主要集中在低频子图,而高频子图对应人脸的边缘与轮廓.所以对人脸识别起主要作用的是低频子图,当然,高频子图从某种程度上也能起到一定识别作用,但从实验来看,和低频子图相比所起的作用要逊色得多.所以,笔者选择某个尺度的低频子图来代替原人脸图像作为训练样本,并用2DPCA进行图像特征提取.
2.2 基于小波变换和2DPCA的人脸识别方法
基于小波变换和2DPCA的人脸识别方法大致分为2步:第1步,对人脸图像数据库中的图像进行小波变换,得到不同尺度的小波子段图像.选择合适的子段图像代替原图像作为训练图像.第2步,对得到的训练图像利用2DPCA进行图像特征提取.为了验证提取出的图像特征的表示能力,采用最近邻分类器进行图像识别.下面给出相应的算法.
算法:基于小波变换和2DPCA的人脸识别算法.
输入:图像数据库.
输出:分类规则.
算法步骤:
STEP1对图像数据库中每1幅大小为s×t的图像fi(x,y)(i=1,2,…,N),利用BIOR3.1做J层小波变换(对不同的图像数据库,J取不同的值,J的取值根据图像的大小确定),N是图像数据库中的图像个数.得到不同尺度的小波子段图像序列{f(J)i,LL,{f(J)i,HL,f(J)i,LH,f(J)i,HH},…{f(I)i,HL,f(I)i,LH,f(I)i,HH}}(i=1,2,…,N).
STEP2根据对图像数据库中的每一幅图像fi(x,y)(i=1,2,…N),选择小波子段图像序列{f(J)i,LL, {f(J)i,HL,f(J)i,LH,f(J)i,HH},…,{f(J)i,HL,f(J)i,LH,f(J)i,HH}}(i=1,2,…,N)中的低频子图f(J)i,LL作为训练样本,设其大小为s′×t′.利用2DPCA方法,提取f(J)i,LL的二维主成分特征.
STEP3在保证一定识别率的前提下,用实验的方法确定主投影方向数d.
STEP4构造图像特征库.设d个主投影方向为x1,x2,…,xd,利用公式yk=Ai xk得到d个主投影特征向量y1,y2,…,yd,其中,A i=f(J)i,LL(i=1,2,…,N).用这d个投影特征向量构造s′×d投影特征矩阵,Y=(y1,y2,…,yd),它是原图像fi(x,y)经W T+2DPCA后提取得到的s′×d的二维模式特征,N个二维模式特征构成了图像特征库.
STEP5用基于矩阵距离的最近邻分类器进行人脸识别.
3 实验结果
为了验证本文方法的有效性,笔者用ORL,YALE和JAFFE 3个人脸数据库作实验比较.ORL人脸数据库中包括40个人的人脸图像.这些人脸图像是在不同的时间、轻微的光线变化、不同的表情(如睁眼、闭眼,微笑、没有微笑等)和不同的表情细节(如戴眼镜和不戴眼镜等)条件下拍摄的.YALE人脸数据库中包括15个人的人脸图像.这些人脸图像是在不同的表情(如悲哀、吃惊、高兴等),和光源在不同位置(如居中、光源在左和光源在右)的情况下拍摄的.JA FFE人脸数据库中包括10个人的213幅不同表情的图像(如高兴、悲哀、吃惊等).因为3个人脸数据库中每类样本数都较少,如ORL人脸数据库中,每个人只有10幅图像,所以实验采用二折交叉验证方法,分类器采用最近邻分类器.实验环境是PC机,双核1.86GCPU,2G内存,W indow s XP操作系统,M atlab 7.1实验平台.实验1,不用小波变换而直接应用PCA和2DPCA方法,在3个数据库上的实验结果如图3所示.实验2,首先对人脸数据库中的人脸图像作一层小波变换,然后用低频子图代替原人脸图像作为样本参与学习.所用小波为双正交小波Bior3.1,在3个数据库上的实验结果如图4所示.从实验结果看,2种方法的识别率基本在同一个数量级,但所用维数后者比前者要低得多,所以基于小波变换和2DPCA的人脸识别方法的计算代价要低得多.

4 结论
针对2DPCA人脸识别方法计算复杂度高、存储系数多这一缺点,利用小波变换具有降2采样和能快速计算的特点,提出了一种新的基于小波变换和2DPCA的人脸识别方法,该方法的识别率与2DPCA相比,大致相当,但可以克服2DPCA的上述缺点,实验结果证明了该方法的有效性.
[1]ZHAO W,CHELLAPPA R,PH ILL IPSP J,et al.Face recognition:a literature survey[J].ACM Computing Surveys, 2003,35(4):399-458.
[2]TURK M,PENTLAND A.Eigen-faces for recognition[J].Journal of cognitive neuroscience,1991,3(1):71-86.
[3]BELHUM EUR P N,HESPANHA J P,KRIEGMAN D J.Eigenfaces vs.Fisherfaces:Recognition using class specific linear p rojection[J].IEEE Transactions on Pattern Analysis and M achine Intelligence,1997,19(7):711-720.
[4]BARTLETT M S,MOV ELLAN J R,SEJNOW SKI T J.Face recognition by independent com ponent analysis[J].IEEE Transactionson Neural Netwo rks,2002,13(6):1450-1464.
[5]W ISKOTT L,FELLOUSJM,MALSBURGC V.Face recognition by elastic bunch graphmatching[J].Transactionson Pattern Analysis and M achine Intelligence,1997,19(7):775-779.
[6]SAMARIA F,YOUNG S.HMM based architecture fo r face identification[J].Image Vision Computing,1994,12(8): 537-583.
[7]LAWRENCE S,GILESC L,TSO IA C,et al.Face recognition:A convo lutional neural-network app roach[J].IEEE Transactionson Neural Netwo rks,1997,8(1):98-113.
[8]YANGJian,ZHANGD.Two-dimensional PCA:A new app roach to appearance-based face rep resentation and recognition [J].IEEE Transactionson Pattern Analysis and Machine Intelligence,2004,26(1):131-137.
[9]ZHANG Daoqiang,ZHOU Zhihua.(2D)2PCA:Two-directional two-dimensional PCA fo r efficient face rep resentation and recognition[J].Neurocomputing,2005,69(1):224-231.
[10]MALLA T S G.A theory fo rmultiresolution signal decomposition:the w avelet rep resentation[J].IEEE Transactionson Pattern Analysis and M achine Intelligence,1989,11(1):674-693.
Face Recogn ition Based on Wavelet Transformsand 2DPCA
ZHAIJun-hai,ZHAIMeng-yao,WANGHua-chao
(College of Mathematics and Computer Science,Key laboratory of Machine Learning and Computational Intelligence,Hebei University,Baoding 071002,China)
Principal component analysis(PCA)has been successfully app lied to face recognition.However,image data must be converted into vecto r w ith high dimension for the PCA based face recognition methods,w hich requires too much time to extract the p rincipal components.Two dimension p rincipal component analysis(2DPCA)directly p rocess image data w ithout step of vecto rization.Compared w ith PCA based methods,2DPCA based app roaches can lower the computational complexity,but much more spaces are need to store the coefficients of 2DPCA.In this paper,based on wavelet transform s(W T)and 2DPCA,an app roach of face recognition was p roposed,w hich could overcome the d raw back mentioned above.The experim en tal results confirmed the effectiveness of the p roposed m ethod.
wavelet transform s;face recognition;p rincipal component analysis;eigenfaces;feature extraction
TP 181
A
1000-1565(2010)05-0574-06
2010-05-10
国家自然科学基金资助项目(60773062);河北省自然科学基金资助项目(F2010000323;F2008000635);河北省应用基础研究重点项目(08963522D)
翟俊海(1964—),男,河北易县人,河北大学副教授,博士,主要从事机器学习与计算智能、模式识别和小波分析方向的研究.
(责任编辑:孟素兰)

