环型空间阵列扭矩传感测量系统研究*

王远干，喻洪麟，巴 军

(1.重庆大学光电技术及系统教育部重点实验室，重庆400044;2.钦州学院，广西 钦州535000)

0 引言

扭矩是最能反映机械传动系统动态性能的典型机械量之一。通过对扭矩的分析，可提取有效反映机械传动系统动态特性的转角、振角、角加速度等主要特征参量［1］。因此，扭矩测量对传动轴载荷的确定和控制，对传动系统各工作部件的强度设计和原动机容量的选择都有着重要的指导意义，是目前国内外学者关注的研究热点之一［2］。

针对目前国内外对强冲击、高温、腐蚀、强振动等极端恶劣环境下机械传动系统的扭矩测量仍无有效检测方法的现状，提出一种基于球对称特性和交流电磁感应原理的扭矩测量方法，采用环型空间阵列和磁电式检测器组成新型的非接触式扭矩传感器［3］，并利用虚拟仪器软件LabVIEW建立同频正弦信号相位差测量系统，以实现极端环境下机械传动系统扭矩的在线动态测量。

1 系统设计

基于环型空间阵列扭矩传感器的测量系统是根据传递测量方法，通过测量机械转轴两端环型空间阵列扭矩传感器输出信号的相位差来获得转轴在扭矩作用下［4］，由于扭转变形而产生的扭转角，从而实现扭矩的非接触式动态测量，系统设计框图如图1所示。

在扭矩测量系统中，环型空间阵列扭矩传感器主要由环型空间阵列和磁电式检测器组成，其结构如图2。环型空间阵列由一个环形非磁性套管构成，管内塞满尺寸和磁特性完全相同的小球，这些小球在套管内紧密排列，形成一个环型空间阵列。磁性小球的具体数量和尺寸根据具体要求和不同测量对象而定。磁电式检测器由铝制外壳封装而成，嵌套在环型空间阵列外部，内部有一个缠绕着特定线圈组的塑料骨架和相应的信号处理电路。

系统工作时，环型空间阵列随转轴转动，位置固定的磁电式检测器沿环型空间阵列滑动，转轴两端加载的环型空间阵列扭矩传感器输出的电压信号频率相同但相位不同，其差值反映了转轴在扭矩作用下由于扭转变形而产生的与扭矩呈线性关系的扭转角。因此，可通过数据采集系统，将环型空间阵列扭矩传感器输出的模拟信号转变成数字信号［5］，利用计算机比较转轴两端传感器输出信号的相位，得到转轴在扭矩作用下产生的扭转角，然后，根据扭矩和扭转角的函数关系计算得到扭矩的测量值，从而实现扭矩的在线动态测量。

2 扭矩测量原理

2.1 交流电磁感应原理

由传感器结构可知，环型空间阵列扭矩传感器主要是基于交流电磁感应原理，实现机械传动系统的位移信息向电信号的转换［6］。图3给出了线圈的互感原理图。

假设在磁芯上绕有2个线圈N1和N2，当匝数为N1的初级线圈通入激励电流i1时，初级线圈中产生自感应磁通Φ11，其中将有一部分磁通Φ21穿过匝数为N2的次级线圈，从而在次级线圈中产生互感电动势u21，其表达式为

式中 ψ21为穿过N2的磁链，ψ21=N2Φ21=M0i1;M0为两线圈的互感系数。

当激励电流为正弦稳态形式且其角频率为ω时，可用向量表示其伏安关系为

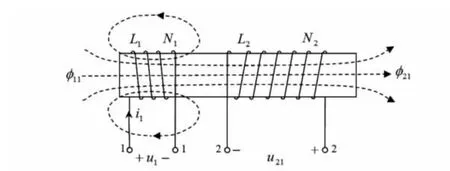
图3 互感原理图Fig 3 Principle diagram of mutual inductance

从环型空间阵列扭矩传感器的结构可以看出:当机械转轴在扭矩的作用下转动时，磁电式检测器将相对于环型空间阵列运动［7］。随着线圈之间磁介质的变化互感系数也会产生相应的变化，那么，输出电压的幅值也会发生变化，从而实现环形位移信息到电信号的转换。

2.2 球对称特性分析

根据2.1所述，磁电式检测器中采集线圈感应电压的幅值正比于激励线圈和采集线圈之间的互感系数，而互感系数一般与磁路性质有关。在该传感器的设计中则与磁性小球切割磁力线的截面积有关。在一个球距内，由于不同位置的磁性小球切割磁力线的截面积呈周期性变化，因而，磁导率会呈周期性变化。线圈采集到的感应电压，亦随之变化。由磁电式检测器内部线圈的排列规律可知，在一个球距内，同组的绕向相同的4个采集线圈采集到的感应信号将满足一定的位置关系。例如:当一个感应信号在波峰位置时，对应的另一个感应信号应在波谷位置。相邻2个采集线圈的感应信号幅值的变化曲线相位差90°。

利用ANSYS有限元分析软件对环形空间阵列扭矩传感器进行二维建模和电磁分析［8］，其平面模型如图4所示。

图4 环形空间阵列平面模型Fig 4 Plane model of ring-space array

在图4中，A1区域为激励线圈;A2，A3，A6区域为磁性钢球;A7区域为非磁性不锈钢管;A4，A5，A8区域为管内外空气。对不同区域赋予不同的材料特性，再施加磁力线平行边界条件和5 V，1 kHz的交流电压作为载荷，然后进行仿真计算，图5给出了磁场分布情况。

图5 磁场分布Fig 5 Magnetic field distribution

从图5中可以看出，当激励线圈固定不动时，磁性钢球中的磁感应强度几乎相等，只有不同位置的磁通量不同，并在一个球距内呈周期性变化。根据公式ψ=Mi，相应的互感系数M在空间上也将呈周期性变化。因此，当磁电式检测器相对于环形空间阵列运动时，输出信号的相位将随其在0°～360°之间变化。

2.3 传感器数学模型

由2.2节分析可知，如果转轴在受到扭矩的作用时检测器相对于环型空间阵列产生了x的环型位移，那么，M0可表达为

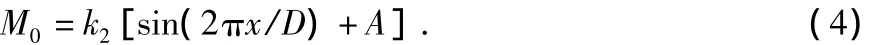
当u1=U1msinωt时，4个次级线圈感应电压的有效值分别为

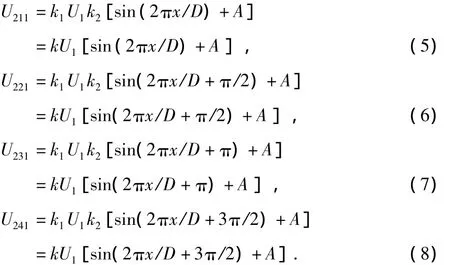
其中，k为比例系数，A为互感系数产生的直流分量。由此说明，4个次级线圈感应信号的幅值均受环型位移x的调制，且各有90°的相位差。图6给出了四路信号的处理简图。

从图6可以看出:四路调幅信号经过两两相减、移相再相加，便可转换成相对于激励信号正比于环型位移量x的调相信号

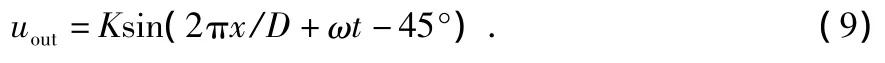
由式(9)可以看出:机械转轴受到扭矩的作用时，转轴两端加载的环型空间阵列扭矩传感器输出的电压信号频率相同但相位不同［9］，其差值正是转轴的与扭矩呈线性关系的扭转角φ。因此，可通过比较转轴两端传感器输出信号的相位，得到转轴在受到扭矩作用时产生的扭转角φ。然后，根据扭矩和转轴扭转角的关系计算得到扭矩的动态测量值。

图6 信号处理简图Fig 6 Diagram of signal processing

3 实验结果

在机械传动实验台上，对环型空间阵列扭矩传感器测量系统进行了相应的扭矩测量实验。将2个球直径均为12.7 mm的环型空间阵列安装在跨距为1 m的转轴的两端。激励信号为5 V，1 kHz的电压信号，用5.08 MHz的时钟脉冲填入到1 kHz标准方波与调相信号方波的相移空间内，经计数器获得5080倍细分值，由计算机采集处理，利用Lab-VIEW构建相位差测量系统，系统可测量最小扭转角≤±0.01°。

表1是用该扭矩传感器对一组具有标准扭矩值载荷进行测量得到的实验数据。由表可得，该扭矩测量方法具有较高的精度，测量相对误差≤0.5%。

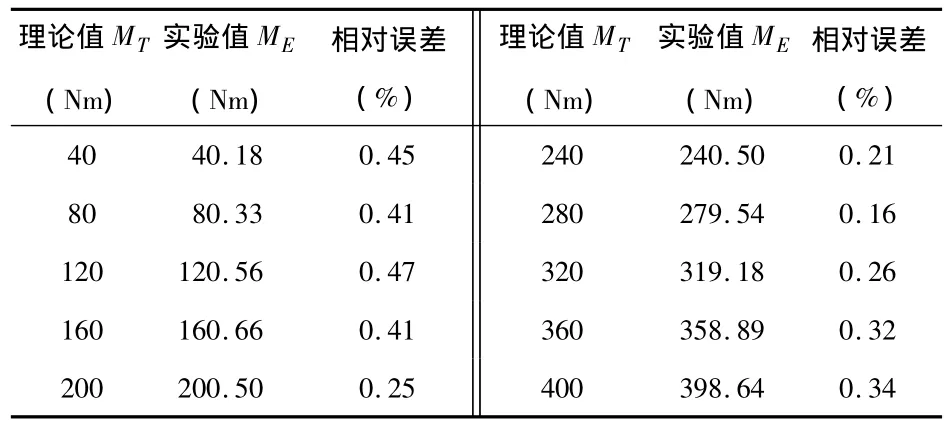
表1 实验数据Tab 1 Experimental data

4 结论

本文提出一种基于球对称特性和交流电磁感应原理的非接触扭矩测量方法，采用环型空间阵列和磁电式检测器组成新型的非接触式扭矩传感器，并对该测量系统的测量原理和设计框架进行了分析，通过电磁仿真分析与实验验证，该测量方法切实可行，所设计的扭矩传感器具有较好的线性度，测量相对误差≤0.5%，可满足恶劣环境下机械转轴扭矩的在线动态测量。

［1］Salach J，Bienkowski A，Szewczyk R.The ring-shaped magnetoelastic torque sensors utilizing soft amorphous magnetic materials［J］.Journal of Magnetism and Magnetic Materials，2007，316:607－609.

［2］Lee J Y，Kauh S K，Ha K P.Development of a disc-type torque meter for an automatic transmission vehicle［J］.Journal of Automobile Engineering，2005，219(12):1443－1449.

［3］黄 震，刘 彬，董全林.基于激光多普勒技术的扭矩测量研究［J］.计量学报，2007，28(1):61－63.

［4］喻洪麟，刘旭飞，吴永烽.光栅扭矩传感器的信号电路设计［J］.光电工程，2005，32(8):93－96.

［5］Madni A M，Hansen R K，Vuong JB，et al.A differential capacitive torque sensor(DCTS)［J］.IEEE Transactions on Sensors，2005(1):1286－1289.

［6］Beckwith T G，Marangoni R D，Lienhard JH.机械量测量［M］.王伯雄，译.北京:电子工业出版社，2004.

［7］金贺荣，郑德忠，何 群.基于虚拟仪器的翻车机传动系统扭矩测试算法研究［J］.传感技术学报，2007，20(3):694－697.

［8］孙明礼，胡仁喜.ANSYS10.0电磁学有限元分析实例指导教程［M］.北京:机械工业出版社，2007.

［9］Masayuki K，Hiroyuki O.Running torque of ball bearings with polymer lubricant［J］.Transactions of the Japan Society of Mechanical Engineers C，2005，71(701):272－279.