双交通模式随机用户平衡问题的一种求解方法*
度 巍 王先甲 黄崇超 肖海燕
(上海金融学院应用数学系1) 上海 201209) (武汉大学系统工程研究所2) 武汉 430072)
(武汉科技大学冶金工业过程系统科学重点实验室3) 武汉 430081) (武汉大学数学与统计学院4) 武汉 430072)
(湖北第二师范学院数学与计量经济系5) 武汉 430205)
0 引 言
交通分配是交通规划理论的基础,自20世纪50年代Wardrop[1]提出著名的平衡交通分配两原则以来,国内外众多学者对于交通分配进行了大量研究.在Ward rop的用户平衡配流原则中,总是假设出行者精确地了解每条路径的出行时间,从而始终能做出绝对正确的路径选择.而事实上,由于信息掌握得不充分,出行者只能对路径出行成本作出大致估计,对同一路径,不同的出行者会有不同的估计值.Dagazno和Sheffi[2]将出行者对路段出行成本的理解值与实际值之差视为随机变量,给出了随机用户平衡(SUE)概念,此后许多学者对于随机用户平衡问题进行了深入研究[3-5].文献[4]首次将交通分配问题从以往的单交通模式扩展到更符合实际的双交通模式,其中一种为主交通模式(通常为轿车,出租车),另外一种为次交通模式(通常为轨道交通),次交通模式上的行走阻抗为固定值.同时构造了在模式分离情形下,一种求解双交通模式确定性用户平衡问题的方法.然而当主要交通模式采用随机用户平衡分配时,尚无有效的求解方法,本文通过在次交通模式路径上定义虚拟路阻函数,将双交通模式的交通分配问题转化成为通常的单交通模式下的固定需求随机用户平衡问题求解,最后给出了一个算例.
1 基本网络描述
定义交通网络G=(N,A,M).式中:N为节点集合;A为有向路段的集合;M为交通模式数,本文将考虑M=2时的情况.a为G中主交通模式的任意一条路段;xa为路段a上的主交通模式流量;ca(xa)为路段a的路阻函数,为单调递增函数;W为G中的O-D对集合;w为W中的任一O-D对;Pw为主交通模式中O-D对w间的所有路径集合;¯Dw为O-D对w间的交通需求;Dw为O-D对w间主交通模式的交通需求;k为主交通模式中属于Pw的任意一条路径为O-D对w间路径k上的主交通模式流量;表示若路段a在连接O-D对w的路径k上,则为1,否则为0;为O-D对w中,主交通模式出行者对路径k的估计阻抗,ckw为w中主交通模式路径k的实际阻抗.
由于次交通模式在各个O-D对w的每条路径上,其行走阻抗为定值,所以可以认为次交通模式在各个O-D上仅有一条路径,该路径只含一条路段直接连接各个O-D对,定义该路段为aw,其运行阻抗为定值cw,其路径上的流量为 fw,图1是一个4O-D对的双交通模式路网图.
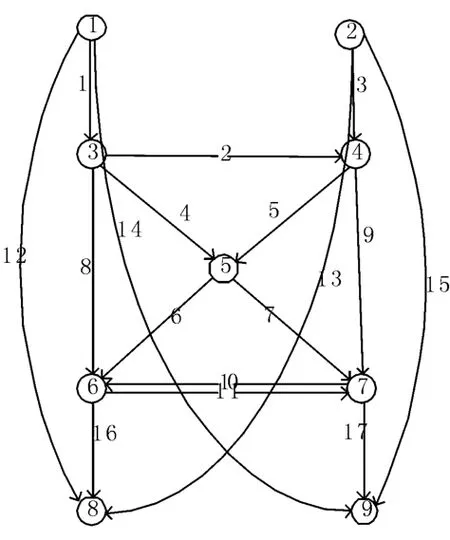
图1 双交通模式网络图
图1 中4个O-D对分别为1-8,1-9,2-8,2-9,其中直接连接各个O-D对的路径为次交通模式的路径,在双交通模式下有以下条件成立

当双交通模式下的交通分配达到随机用户平衡时,对主交通模式,各个O-D对路径交通流应满足如下Logit分配方式


在主交通模式与次交通模式之间,若移植固定需求下的双模式交通需求分配模式,达到随机用户平衡时,应满足如下关系w

式中:θ2为交通模式之间的比例参数.
2 问题求解
由于双模式随机用户平衡问题不仅要在主交通模式内部,而且还要在交通模式之间达到随机用户平衡,所以使得平衡交通流的求解变得复杂,下面的定理1将说明,通过对次交通模式路径赋以适当的虚拟路阻函数,可以将双模式随机用户平衡问题转化成为通常的单模式固定需求随机用户平衡问题.
定理1 在路网中,若对次交通模式的路径(即直接连接O-D对w的路段)赋以如下虚拟路阻函数

以θ1为Logit比例参数,¯Dw为交通需求的单模式随机用户平衡(SUE)问题的平衡路径流,与双模式随机用户平衡交通流相同.
证明 令 fw*为交通路网在单模式、固定需求下达到随机用户平衡时,次交通模式的路径流量 ,由式(6),有

将式(9)代入式(10)得
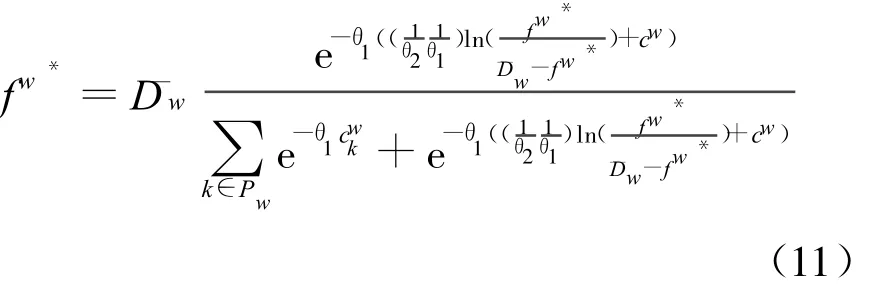
即

化简得

进一步有

即

最后得
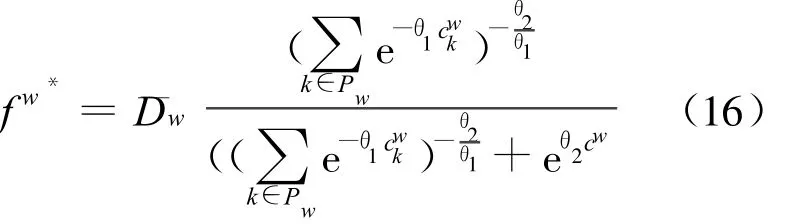
由式(16),可得

由式(3)与式(17),可得
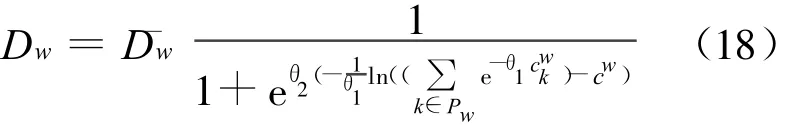
式(18)正好是双模式弹性随机用户平衡时,两模式之间的分配关系式(8).
对于原主交通模式的路径,不失一般性,考虑O-D对w的路径k.当达到单模式、固定需求下的随机用户平衡时,其平衡流fw*k 应满足

将式(9)代入式(19)有

将式(17)代入式(20),化简得

整理式(21),得

由式(18)知式(22)即为

式(23)表明,在网络中,当达到单模式、固定需求下的随机用户平衡时,原主交通模式的各个路径平衡流也与双模式随机用户平衡流相同,从而定理获证.
3 双模式随机用户平衡问题的数学规划模型

由于定义的路阻函数是可分离的,该问题对应的数学规划模型可以证明数学规划(24)的K-K-T条件满足双交通模式下的随机用户平衡条件,即式(6),式(8).
同时式(24)关于变量的Hessian矩阵为

对式(9)关于 fw求导,得

由于次交通模式的运行阻抗为固定值,从而出行者对于交通模式之间运行阻抗的观察误差比例系数θ2不大于出行者在主交通模式中各O-D对路径间的观察误差比例系数θ1,从而式(29)大于零,故H essian矩阵正定,从而数学规划(24)为严格凸规划,存在唯一解.
4 算 例
最后通过求解图1所示的交通路网所对应的双模式随机用户平衡配流,检验本文提出方法的可行性.
交通网络1中,各个O-D对交通需求量及有效路径集合如表1所列,表中括号内是路径所包含的路段.
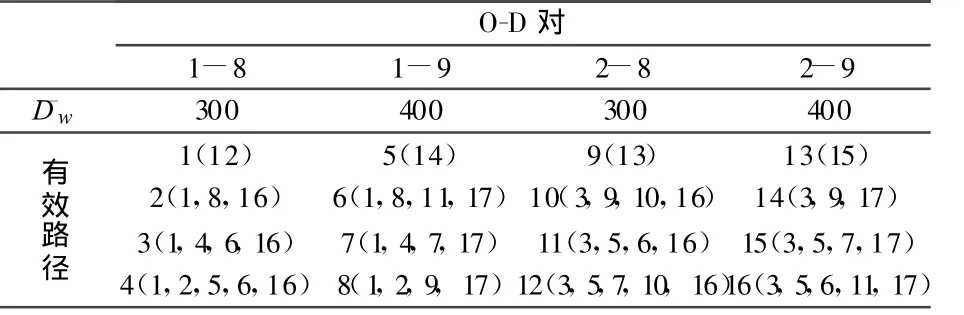
表1 路径列表
对上述双模式随机用户平衡交通分配问题所对应的数学规划模型,本文用仿射尺度内点算法求解[8-11].该算法的思想是:对于当前迭代点Fk=(,…,构造对角阵 D k=diag(,…),作仿射尺度变换 Tk:g=D k-1Fk,在此变换下,式(24)变为如下形式

式中:¯A k=AD k,A为式对应的约束矩阵;b为O-D需求向量.在仿射尺度变换下,Fk将被变换到(26 b)的约束区域的中心e=(1,1,…,1)T,从e出发沿式(26 a)的目标函数在gk=e处的负梯度在矩阵¯A k核空间的投影方向作一维搜索,得新的可行内点Fk+1.
算法迭代步骤如下.
步骤1 取初始可行路径配流F1=(fw1,11,…,fwnm,1)T,允许误差ε>0,置迭代数k=1.
步骤2 由Fk构造对角阵Dk=diag,…,fwnm,k),计算▽G k(e)=D k▽F(fk),A¯ k=ADk,

步骤3 若▽′G k(e)=0或者‖ ▽′Gk(e)‖<ε,最优配流为 Fmin,=Fk=Dke算法停止,否则转步骤4.
步骤5 设λk为一维搜索得到的最佳步长,令Fk+1=Fk+λKDkdk,k:=k+1,转步骤2.
在本算例中,取θ1=2,θ2=1,而各路段自由流阻抗分别为[5 6 5 3 3 4 4 6.5 6.5 7 7 16 21 16.5 22 5 5].求得的双模式随机用户最优配流结果如表2所列.

表2 双模式随机用户最优配流结果
5 结 束 语
本文通过对次交通模式上的路径赋以虚拟路阻函数,将双交通模式随机用户平衡问题转化成单模式随机用户平衡问题求解,并用仿射尺度内点算法对一个小型路网进行了数值实验.当次交通模式的出行路阻为变量时以及当交通模式多于两个时所对应的随机用户平衡交通分配将是下一步的研究方向.
[1]Wardrop JG.Some theoretical aspects of road traffic research[J].Proceedings of the Institute of Civil Engineers,1952(2):325-378.
[2]Daganzo CF,SheffiY.On stochasticmodels of traffic assignment[J].Transportation Science,1977,11(3):253-274.
[3]Sheffi Y.U rban transportation netw orks:Equilibrium analysis w ith mathematical p rogram methods[M].New Jersey,Prentice-Hall,INC,Englewood Cliffs,1985.
[4]Florian M.A traffic equilibrium model of travel by car and pub lic transitmodes[J].Transportation Science,1977,11(2):166-179.
[5]Gartner N H.Op timal traffic assignment with elastic demands:A review;Part II:A lgorithmic approaches[J].Transportation Science,1980,14(2):192-208.
[6]度 巍,王先甲,黄崇超.一种求解弹性需求随机用户平衡问题的新方法[J].上海交通大学学报,2009,43(2)230-234.
[7]周 晶.随机交通均衡配流模型及其等价的变分不等式问题[J].系统科学与数学,2003,23(1):120-127.
[8]陈森发,周 晶,朱玉全.城市交通均衡流分配的多模式模型及算法[J].自动化学报,1993,(12):190-196.
[9]Huang CC,JiC M.Gradient projectionmethod with affine scaling for non linear programm ing[J].Advances in Modeling&Analysis,1994,22(2):43-48.
[10]四兵锋,高自友.多模式的城市混合交通均衡配流模型及算法[J].公路交通科技,1999,16(1):44-48.
[11]刘海旭,蒲 云.多类型弹性需求随机用户平衡分配模型[J].系统工程理论方法应用,2005,14(2):159-165.

