基于有限记忆的智能群体群集运动控制*

王冬梅 方华京

(华中科技大学控制科学与工程系 武汉 430074)

近年来,群集行为引起了研究人员的极大关注,逐渐成为复杂性科学研究的一个焦点.Reynolds[1]最早给出了构成群集行为的3条基本规则,称之为 Reyno lds模型.在此基础上,Vicsek[2]提出了一种基于速度匹配规则的简单群集模型.基于这2个模型研究者展开了大量的研究:Tanner,R.O Saber,Long Wang等学者[3-6]从二阶系统的角度研究了Reynolds模型,通过构建微分方程组将群集运动进行抽象化实现了群集运动控制.而 Jadbabaie,Moreau,W.Ren等[7-8]则运用动态图理论研究解决了Vicsek模型的收敛性问题.

由于互异的个体状态表现出了互不相同的个性特征,个体在运行过程中除了主要根据邻近规则的决策下一步行为外,还应根据各自的个性特征进行判断和决策;个体的运行状态应由个体的内部和外部环境同时决定.

本文旨在初步探讨个体的个性特征即内部因素对群集行为的影响.通过引入具有记忆能力的智能个体,利用记忆能力总结个体运动的历史“经验”,并估计将来的运动趋势.通过若干记忆单元记录该个体最近的历史状态信息,根据历史状态信息在线预测估计个体的下一时刻的运行状态,并以此作为虚拟领航者引导群体运行.仿真结果表明有记忆的智能群体最终以较快的速度形成稳定的群集运动;但在稳定运行阶段个体的状态在稳态附近上下波动,这与自然界群集现象相吻合.

1 基于有限记忆的智能群体的群集控制

1.1 最小二乘估计理论

最小二乘法是一常用回归方法.基本思路是令f(X)=a1 h1(X)+a2 h2(X)+…+am hm(X)式中:{hk(X)}(k＜N)是一组事先选定的线性无关的函数;{ak}mk=1是一组待定系数.寻求系数{ak}m

k=1使得Yi与f(Xi)的距离di的平方和最小.该方法最关键的一步是恰当地选取线性无关的基函数{hk(X)(m＜N).通过对基本群集运动的理论分析和实验仿真发现,群体经过起初短暂的无秩序运动之后,群体将以相同的速度按近似的线性轨迹运行;而且由于个体的运动轨迹在较小的采样周期内可以用直线近似,因此可以采用线性回归这种简单的预测模型.

设某个个体的位置为 p=(x,y)T,个体的运行轨迹在较小的采样周期T内与时间t成线性关系,则线性回归方程

当m个记忆单元存满时,根据m次观测数据(tk,pk),用最小二乘法求出a,b,c,d的估计值.

式中:a,b,c,d为未知待估参数.从t1时刻开始,以较小的采样周期T=tk+1-tk,(K=1,2,…,m)为时间间隔;通过m次观测利用m个记忆单元存储时间和位置信息(tk,pk),得到

根据a,b,c,d的估计值,利用式(1)估算t=tm+1时刻个体的位置信息.由于个体运行轨迹不断的变化,因此应采用新的观测数据去刷新历史数据重新估计a,b,c,d的值以减小误差.方法是当tm+1时刻个体的位置信息 pm+1的实际值产生时,遗弃记忆单元中最初的t1时刻的采样值,利用t2至tm+1之间的观测值重新估计a,b,c,d,根据新的a,b,c,d估计值预测新时刻的个体位置信息.依此类推,记忆单元总是存储记录最近m个时刻的较小采样周期时间内的个体状态信息.

1.2 智能群体的群集控制

本文采用虚拟领航者策略利用具有记忆能力的智能个体记录个体先前的位置信息,以此模拟个体的运行过程中积累的“经验”,根据该“经验”预测估计下一步的运行状态,以该状态作为虚拟领航者引导个体运行,个体的“经验”反映了内部环境的影响.

在建立群体模型之前,首先给出以下定义.

定义(邻接图G) 邻接图G(V,ε(p))是一个无向图.其中:V={n1,…,nN}表示顶点集;ε(p)={(ni,nj)∈V×V}表示边集,由个体间的邻接关系确定.

考虑由N个个体组成的群体,其动态方程为p i=q i,q i=u i,i=1,2,…,N.其中:p i为个体的位置;qi=(xi,yi)T为速度向量,ui=(uxi,uyi)T为控制输入;p ij=p i-p j为个体i,j间相对位置矢量;‖p ij‖为个体i,j间的相对距离.

群集运动是一种基于势场原理的运动,它的控制由两部分来实现:u i=ai+βi,i=1,2,…,N.式中:ai由人工势能来实现,用于控制个体间的距离实现避碰和聚集;βi用于调整个体的速度使群体的速度匹配.第i个体的虚拟领导者的状态用(piL,qiL)进行描述,根据个体最近m个时刻用最小二乘估计产生.

式中:Ni为i个体的邻居集,NiΔ={j:‖p ij‖≤R}⊆{1,2,…,N},R为个体的通讯作用能力;k1为常数.在群集运动中个体的运动状态同时取决于个体的内外部环境,但外部环境(周围邻近个体的状态)起主导作用,故体现个体内部因素的作用项的系数k1应在(0,1)范围内;U ij为势能函数,是关于个体i与j之间的相对距离‖pij‖的非负、可微函数,是关于个体i与其虚拟领航者间的势能函数.均应满足:当‖pij‖→0,Uij(‖pij‖)→∞;当个体i与j之间的相对距离‖p ij‖达到一定值时,U ij取得惟一最小值.

由于在(p,q)坐标系下,系统的解最终将趋向无穷、无界.故将系统转换到相对坐标系(r,v)下,即 ri=pi-p,vi=qi-q,其中 p,q表示群体的

2 稳定性分析

下面基于LaSalle不变原理给出该模型的稳定性分析,考虑如下的半正定函数:W=

定理 考虑一个由N个个体组成的群体,其运动控制律由式(3)描述,假设群体所对应的邻接图G是连通的,那么所有的个体最终能够达到速度矢量相等,相互间的距离稳定,并且个体之间不发生碰撞,群体内部的总势能达到最小.

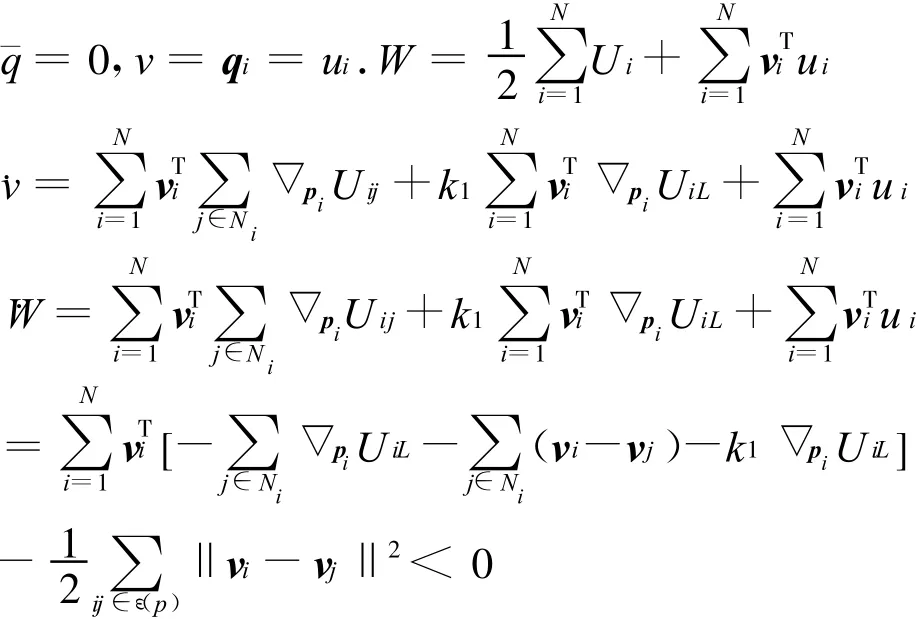
由LaSalle不变原理可知:如果系统的初始状态在集合Ω内,系统的轨迹将收敛到区域S={(r,v)∈Ω:W=0}内的最大不变集.因此,由 W=‖vi-vj‖2＜0可知,群体进入稳定状态时,v1=v2=…=vN,且所有个体收敛到固定位置p*,使得总势能∑V(p*)达到最小值.

3 仿真与分析

本文选取5个具有相同二阶动态性能的个体,在MATLAB环境下进行仿真.在保证群体对应的连接图G连通的前提下,个体随机分布在[-2.5,2.5]的矩形区域内,初始速度大小在(0,1)的范围内.R=2,A=5,L=1.

在初始条件相同的情况下,本文进行了两组比较仿真实验.第一组实验比较了无记忆和有记忆两群体的运动特性.(如图1～图4所示)实验结果显示两群体最终均以较快的速度形成稳定的群集运动;但在稳定运行阶段有记忆群体的个体的状态在稳态附近的波动幅度较大.证实了群集现象中个体的内部因素对群集运动存在着影响.第二组实验对内部因素作用项-c▽piViL的影响程度进行了比较仿真(如图5～图6所示),结果显示当增大作用项的系数c时,个体的状态在稳态附近的波动幅度加大;因此应限制该项的大小使它小于外部因素的影响,原因在于内部因素反映了个体的个性特征,当个体的个性特征太突出时,群体将较难达到协调一致.这与现实中太有个性的群体难于领导达到共识的现象相吻合.

图1 无记忆群体的运行轨迹

图2 无记忆群体的速度收敛过程

图3 C=0.2时有记忆群体的运行轨迹

图4 C=0.2时有记忆群体的速度收敛过程

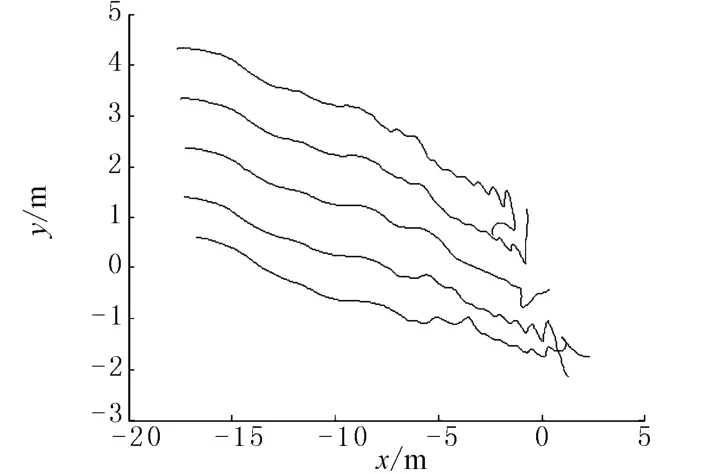
图5 C=0.45时有记忆群体的运行轨迹

图6 C=0.45时有记忆群体的速度收敛过程

4 结 论

本文提出了具有记忆能力的智能群集控制模型,通过记忆单元的信息预测估计个体的运行趋势,并以此作为虚拟领航者引导群体运行.该模型反映了群集运动中个体不仅受局部外界环境影响,同时也受个体的自身内部环境因素的影响.

[1]Reynold CW.FIocks,herds and school:a distributed behavioralmodel[J].Computer Graphics,1987,2l(4):25-34.

[2]V icsek T,Czirok A,Jacob E,et al,Novel type of phase transition in a system of self-deriven particles[J].Physical Review Letters,1995,75(6):1226-1229.

[3]Tanner H,Jadbabaie A,Pappas G J.Flocking in_xed and switching networks[J].IEEE Transactions on Automatic Control,2007,52(5):863-868.

[4]Saber R O.Flocking for multi-agent dynam ic systems:A lgorithms and theory[J].IEEE Transactions on Automatic Control,2006,51(3):401-420.

[5] Wang Long,Shi H ong,Chu Tianguang.Flocking contro l of groups of mobile autonomous agents via local feedback[C]//Proc of the 2005 IEEE International Symposium on Intelligent Control.Limasso l,Cyprus,2005.

[6] Jadbabaie A,Lin J,Morse A S.Coordination o f groups ofmobile agents using nearest neighbor ru les[J].IEEE Trans on Automatic Contro l,2003,48(6):988-1001.

[7] Moreau L.Stability of multi-agent systems with time-dependent communication links[J].IEEE Trans on Automatic Control,2005,50(2):169-182.

[8]Ren W,Beard RW.Consensus seeking inmu ltiagent systems under dynam ically changing interaction topologies[J].IEEE Trans.on Automatic Contro l,2005,50(5):655-661.