聚合物熔体矩形流道挤出胀大的数值模拟

李 勇,郑建荣

(华东理工大学机械与动力工程学院,上海200237)

聚合物熔体矩形流道挤出胀大的数值模拟

李 勇,郑建荣

(华东理工大学机械与动力工程学院,上海200237)

运用Picard迭代格式的有限元方法,采用Wagner积分型本构方程对黏弹流体挤出胀大进行三维模拟分析。每次迭代根据新的自由面边界位置重新划分网格,由前一次迭代得到的速度场,算出单元高斯点流线,沿流线积分计算应力,把应力作为拟体力,建立非线性方程组迭代格式。对不同宽度和长度的矩形流道的挤出胀大进行模拟计算,分析了流道宽度和长度对胀大率的影响。结果表明,随着宽厚比的增加,厚度胀大率随之增加;随着流道长度的增加,胀大率逐渐下降。该结果与二维狭缝流道的数值模拟和实验结果比较表明,用该方法对黏弹流体挤出胀大流动进行三维模拟是可行的和准确的。

聚合物;熔体;矩形流道;挤出胀大;数值模拟

0 前言

挤出胀大是黏弹流体在挤出过程中的固有特性,是挤出成型中最被关心的问题之一。挤出胀大现象给塑料挤出机头的设计造成很大困难。挤出胀大的数值模拟对挤出工艺的控制和提高机头设计的品质具有重要意义。

聚合物挤出胀大的数值模拟存在两大困难,即本构方程的选择和自由面的形状。由于Maxwell本构方程相对简单,黏弹流体挤出胀大问题的数值模拟是从研究Maxwell流体的胀大问题开始的,Chang等[1]首先进行了黏弹Maxwell流体挤出胀大的数值模拟研究。另外,Debae等[2]采用改进的混合有限元法(EVSS/SUPG)模拟,得到收敛解的最高Weissenberg数是3.75。

但Maxwell方程本构关系无法描述真实黏弹流体的流变特性,积分型本构方程包含了松弛时间谱,被认为是对复杂流动综合预测能力最强的本构关系,特别是对于挤出胀大问题。而且不会像Maxwell方程那样遇到高Weissenberg数的问题。采用积分型本构方程关键在于应变历史和应力的计算。Luo等[3-4]采用流线有限元法首先对K-BKZ类模型的熔体挤出胀大进行模拟,并在本构方程中又引入拉伸系数谱,准确拟合了熔体的单轴拉伸黏度。Goublomme等[5]同时用Wagner模型和PSM模型计算了高密度聚乙烯(PEHD)熔体的挤出胀大流动。计算中发现,用Wagner模型更能够准确地预测实验结果,而且胀大比随着模型中表征剪切流动的参数和表征拉伸流动的参数的增大而单调降低。Kiriakidis等[6]采用基于常规有限单元的应变历史跟踪方式计算黏弹应力,模拟了PE-HD(PSM模型表征)和线形低密度聚乙烯(PE-LLD)熔体经过狭缝口模的挤出胀大,结果表明,口模的长宽比显著影响黏弹流体挤出胀大的结果,PE-HD熔体的挤出胀大程度随着流率的增加而增大,计算结果与实验值十分吻合,肯定了K-B KZ类模型能够准确地预测黏弹流体在口模内的应力松弛过程。目前,挤出胀大的研究主要集中在二维流动,对于机头流道中流动的三维数值模拟有一定研究[7-9],但对于挤出胀大的三维数值模拟,由于自由面的确定和网格划分的复杂性,处理起来较为困难,研究较少。

在前期的研究中[10],曾采用应力增量迭代方法和流线有限元方法,对三维挤出胀大进行了初步研究,本文采用Wanger积分型本构方程,运用Picard迭代并根据矩形流道特点使用自由面流线迭代和内部网格重新划分相结合的方法对矩形流道的挤出胀大进行了细致分析,得到了流动的速度场、流线和挤出胀大的三维形状。

1 控制方程

根据挤出加工的特点,聚合物熔体等温、蠕变流动运动方程为:

连续性方程:

本构方程采用Wagner给出的积分型本构方程[11],其应力由式(3)给出:

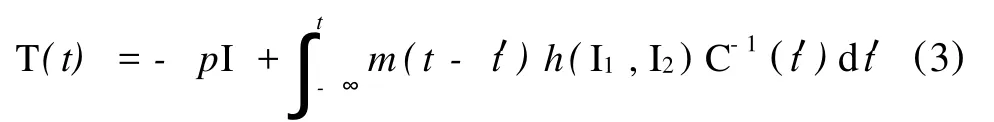
式中 T(t)——应力张量

p——静压力,Pa

τ——偏应力张量,Pa

V——速度向量,m/s

I——单位矩阵

m(t-t′)——代表时间依赖性的记忆函数,由材料的黏弹性数据决定

C-1——Finger应变张量,是Cauchy张量C的逆

I1——C-1的第一不变量

I2——C的第一不变量

h(I1,I2)——非线性的衰减函数

t——当前时间,s

t′——时间的积分变量,s

记忆函数m(t-t′)是松弛时间的函数,可以近似地表达为不连续的时间段的迭加:

式中 ai——松弛模量,Pa

λi——松弛时间,s

对于任意变形的流动,要求给出h与I1、I2之间的关系,定义:

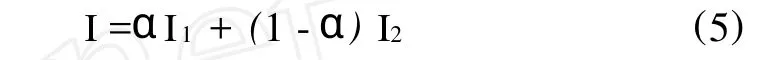
其中α=0.32,有:

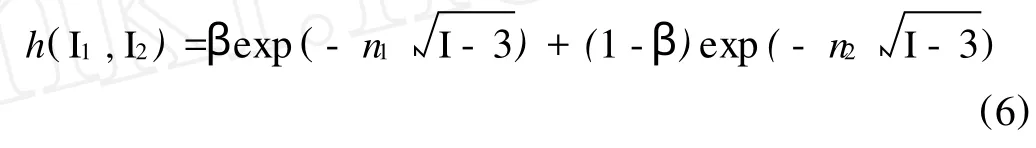
对于PE-LD熔体,式(6)中β=0.35,n1=0.31,n2=0.106。

2 数值方法

2.1 非线性本构方程的迭代

熔体本构关系的非线性特性,是高分子流体挤出问题的主要困难之一。主要解决方法分为两类:第一类是混合法,即把应力、速度和压力作为未知量一起求解;另一类称分裂格式,即Picard迭代,它仅把速度和压力作为未知量求解,用前一次迭代的速度场计算非牛顿应力,再把应力项当作拟体力处理。该方法虽然迭代次数多、但迭代格式实施简单、成熟,一次求解的未知变量小于混合格式,计算量低,同时易于方便地结合微分型或积分型本构方程以及通过分子模型表达的应力关系进行黏弹流体流动数值模拟,由于应力不能表达成速度的显函数,所以本文采用后一种方法,以速度矢量(ν)和压力(p)为未知量,对式(1)、(2)采用Galerkin弱解形式,由于应力不能表达成速度的显函数,所以把应力项放在方程的右端,建立迭代格式:

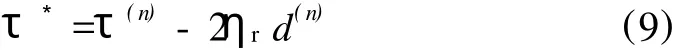
式中 φu——速度的形函数

φp——压力的形函数

Γ——积分区域Ω的边界

ηr——参考黏度,Pa·s

τ(n)——由第n次迭代结果ν(n)、pn通过本构方程计算得到

d——应变速率张量,s-1

N——面力,Pa

f——体力,N/m3

2.2 自由边界的迭代方法

自由边界的边界条件为混合边界条件,即应力和法向速度都为零,所以边界线就是流线。积分型本构方程的熔体二维挤出胀大的模拟大都采用流线有限元方法[3-4],即沿着流线划分网格。它利用自由边界为流线这一性质,先假定自由边界位置,根据应力边界条件求解,得到速度分布,对速度分量积分,得到流线即新的自由边界,同时内部节点也沿流线分布。由于每次迭代中计算出的速度结果并不是最终速度,所以每次迭代都采用速度场计算内部节点流线的意义不大,收敛速度较慢。并且由于三维自由面的形状相对于二维曲线复杂得多,当速度存在误差时,如果积分步长过大会造成单元网格畸形。所以,对于三维情况,本文仅对边界流线进行迭代求解,以计算自由面位置,每次边界更新后,重新对网格进行自动划分,确定内部节点,所以内部节点并不沿流线分布。计算中采用了网格自动划分技术,对矩形流道的单元网格自动划分。

设x为流动方向,则新的自由面由式(10)、(11)得到:

2.3 单元内部流线的计算

应力的计算有2种方法,Tanner沿流线即单元边界积分计算应力,而范毓润进行改进,采用沿通过高斯点的流线进行积分的方法。本文由于在每次迭代时单元内部的节点由网格自动划分得到,所以节点和高斯点并不沿流线分布,必须首先得出单元高斯点流动轨迹,再沿轨迹积分计算应力。根据速度场,可计算高斯点流线。稳态流动质点的加速度可以通过速度表达为:

根据式(12)可以一步步地给出当前时刻t在高斯点的质点的流动轨迹,用张量表示为:

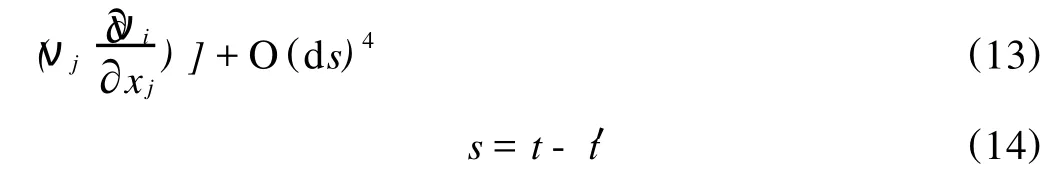
式中 x′i——质点在时刻t′的坐标

式(13)中上标1表示在xi1处的值,而xi1则由式(15)给出:

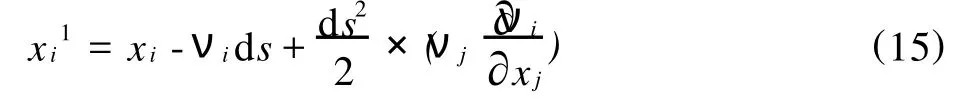
根据式(13)、(15)可以一步步地向回求出质点的位置,公式具有三次精度,另外时间推移量要尽量小,因为整个积分包括很多时间步,如果步长较大,每一步的误差会产生较大的累计误差。

3 出口胀大的计算结果

本文采用上述三维自由面迭代方法,对低密度聚乙烯(PE-LD)在180℃时通过矩形流道挤出的挤出胀大过程进行了仔细分析。计算中采用20节点六面体单元,其中速度为20节点,采用二次插值,压力为8节点,采用一次插值。由于计算量较大,计算中最大单元数为432个。

其中自由边界的迭代步长不能过大,自由面经过大约500次迭代,可以达到较高的收敛精度。用该方法进行挤出胀大的自由面迭代,虽然由于内部节点不在流线上,在计算应力时需要根据速度场计算经过高斯点的流线,增加了每次迭代的计算量,但避免了由于局部流线不均匀而可能造成的流体内部单元畸形。本构方程中的材料松弛材特性如表1所示。

表1 PE-LD在180℃时的流变参数Tab.1 Rheological parameters of PE-LD at 180℃

在二维狭缝流动中,出口胀大率定义为在出口外一定位置的流体宽度与出口宽度的比值。对于矩形流道三维流动,定义为流道两个对称面处的胀大尺寸与原流道出口尺寸的比值,其中厚度方向的胀大率为B1,宽度方向的胀大率为B2,对于宽厚比大的流道,B1可用以与二维狭缝流道的胀大进行比较。

首先考虑等截面矩形流道的出口胀大情况,三维网格采用自动划分技术生成网格。挤出平均速度va=1 mm/s,流道宽度(D)为6 mm,流道厚度用H表示。图1～图3分别给出了2种宽厚比(D/H)的流道的有限元网格的胀大图,以及厚度方向对称面上的流线图和速度等值线,其中速度等值线数值是相对于平均速度的数值。

图1 矩形流道挤出形状Fig.1 Shape of the extrudate flowing out of the rectangular channel

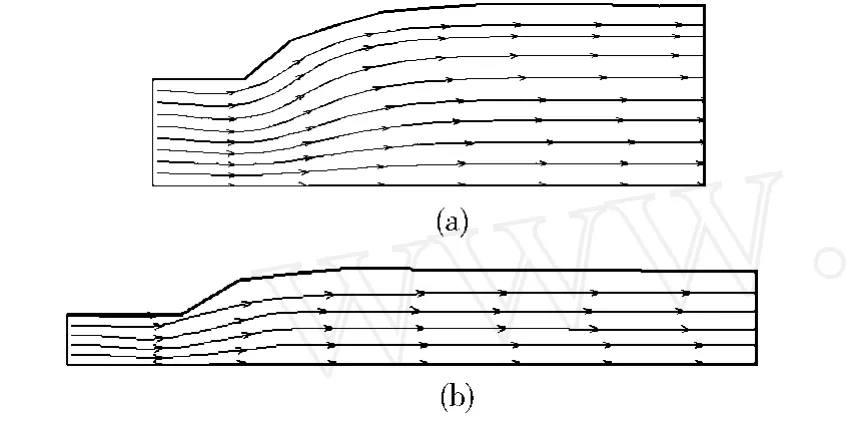
图2 对称面上的流线图Fig.2 Streamline pattern of the symmetrical surface

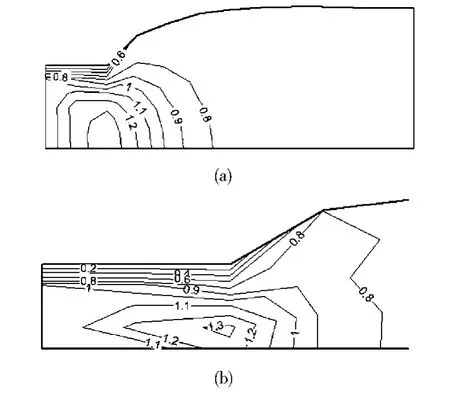
图3 对称面上速度等值线图Fig.3 Axial velocity contour of the symmetrical surface

对不同宽厚比矩形流道的挤出胀大进行分析,在表2中给出出口12 mm处厚度方向胀大率随宽厚比的变化情况。从表2可以看出,随着宽厚比的增加,胀大率B1随之增加,当宽厚比达到6时,厚度的胀大率与二维数值模拟得到的胀大率一致,与实验数据也很接近[12],而宽度方向的胀大率B2则随着宽厚比的增加而减少。

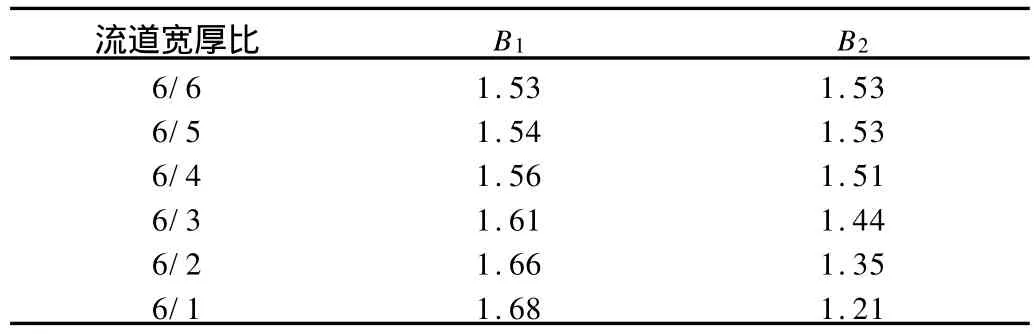
表2 不同宽厚比的矩形流道的挤出胀大率Tab.2 Swell ratio of rectangular channel with differentratio of width to thickness

由于黏弹性流体应力松弛较为缓慢,熔体在流道的停留时间决定应力的松弛程度,所以挤出速度和流道长度对胀大率也有一定的影响。表3给出了不同流道长度的正方形流道挤出胀大率,对于正方形流道,B1与B2相同。可以看出随着流道长度的增加,胀大率逐渐下降,但当流道长度增加到一定程度时,胀大率变化幅度减小。所以流体在流道中的停留时间对胀大率有较大影响。

表3 流道长度对正方形流道挤出胀大率的影响Tab.3 Swell ratio of square channel with different length

对于收敛流道的挤出胀大的分析,考虑2种不同收敛角度的流道,流道总长度相同,为15.6 mm,宽度不变,厚度收敛角分别取作15°和20°。胀大率分别为1.46和1.49,胀大率要大于等截面流道的胀大率1.39,同时由于收敛角为15°的流道的出口流道长度要长些,所以其胀大率小于20°的流道。图4、图5给出了15°收敛流道的挤出形状和流线图。

图4 15°收敛流道的挤出形状Fig.4 Shape of the extrudate flowing out of converging channel with the convergence angle of 15°

图5 15°收敛流道对称面上的流线图Fig.5 Streamline pattern of the symmetrical surface of the 15°converging channel

4 结论

(1)采用自由面迭代结合网格自动重新划分的方法,可以避免流线有限元处理挤出胀大的三维模拟时可能造成的网格畸形,从而较为准确地预测挤出胀大的三维模拟的自由面形状,使挤出胀大的研究更接近实际应用;

(2)PE-LD熔体在矩形流道中的挤出胀大过程呈现出厚度胀大率随宽厚比的增加而增加,胀大率随流道长度的增加而减小的规律;

(3)收敛流道的胀大率大于等截面流道的胀大率。

[1] Chang P W,Pattern T W,Finlayson B A.Collocation and Galerkin Finite Element Methods for Viscoelastic Fluid Flow I.Description of Method and Problems with Fixed Geometry[J].Computers&Fluids,1979,7(4):267-283.

[2] Debae F,Legat V,Crochet M J.Practical Evaluation of Four Mixed Finite Element Methods for Viscoelastic Flow[J].Journal of Rheology,1994,38(2):421-443.

[3] Luo X L,Tanner R I.A Streamline Element Scheme for Solving Viscoelastic Flow Problems Part II Integral Constitutive Models[J].Journal of Non-Newtonian Fluid Mechanics,1986,22:61-89.

[4] Luo X L,Tanner R I.Finite Element Simulation of Long and Short Circular Die Extrusion Experiments Using Integral Models[J].International Journal forNumerical Methods in Engineering,1988,25:9-22.

[5] Goubfomme A,Draily B,Crochet M J.Numerical Prediction of Extrudate Swell of a High-density Polyethylene[J].Journal of Non-Newtonian Fluid Mechanics,1992,44:171-195.

[6] Kiriakidis D G,Mitsoulis E.Viscoelastic Simulations of Extrudate Swell for a HDPE Melt Through Slit and Capillary Dies[J].Advanced Polymer Technology,1993,12(2):107-117.

[7] 柳和生,涂志刚,熊洪槐.聚合物熔体在L型异型材挤出口模内三维粘弹流动数值模拟[J].塑性工程学报,2007,14(2):114-117.

[8] 武停启,江 波,毕 超,等.聚合物熔体全三维非等温数值模拟[J].塑料,2006,35(1):73-79.

[9] 李 勇,江体乾.塑料熔体三维流动的数值模拟[J].中国塑料,2004,18(9):68-72.

[10] 李 勇,江体乾.聚合物熔体三维挤出胀大的数值模拟[J].力学学报,2002,(6):856-862.

[11] Wagner M H,Demarmels A.A Constitutive Analysis of Extensional Flows ofPolyisobutylene[J].Journal of Rheology,1990,34(6):943-958.

[12] Ahmed R,Liang R F,Mackley M R.The Experimental Observation and Numerical Prediction ofPlanarEntry Flow and Die Swell for Molten Polyethylenes[J].Journal ofNon-NewtonianFluidMechanics,1995,59:129-153.

Numerical Simulation of the Extrudate Swell of Polymer Melt Through Rectangular Channels

LI Yong,ZHEN GJianrong

(School of Mechanical and Power Engineering,East China University of Science and Technology,Shanghai 200237,China)

In this paper,the finite element method of Picard iterative format was applied for analyzing extrudate swell of viscoelastic fluid flows in three-dimension using Wager integral constitutive equations.During each iteration,the updated streamline of boundaries was generated according to boundary condition of velocity.The streamline of Gauss point was acquired according to the velocity field of previous iteration.The stress was treated as pseudo-body and the format of iteration was given.Extrudate swells of different width and length of the rectangular die were analyzed.Results of swell ratios influenced by width and length of die were shown.It showed that the swell ratio increased with increasing ratio of width to thickness,and decreased with increasing length of runner.The results were very accurate and were compared with two dimensional numerical simulation and experiments.It proved that this method was efficient and reliable.

polymer;melt;rectangular channel;extrudate swell;numerical simulation

TQ320.66+3

B

1001-9278(2010)02-0078-05

2009-09-06

联系人,yong_li@ecust.edu.cn