联合Delaunay三角网的等高线群综合研究

杨英伟,罗 娟

（1.重庆数字城市科技有限公司,重庆400020；2.重庆市东部新城（鱼嘴组团）建设管理委员会,重庆401133）

联合Delaunay三角网的等高线群综合研究

杨英伟1,罗 娟2

（1.重庆数字城市科技有限公司,重庆400020；2.重庆市东部新城（鱼嘴组团）建设管理委员会,重庆401133）

采用“联合Delaunay三角网”来提取成组等高线的弯曲，在弯曲处利用平三角形连接法进行局部地形结构线的连接，并建立起地形结构线的树状结构。运用方根模型确定谷地选取的数量指标，并提出了一种新的数学模型以确定谷地选取的质量指标，完成等高线群的自动综合。研究和实验表明，该方法充分顾及了地貌形态特征，谷地选取合理，概括程度适当，并完全避免了相邻等高线相交，综合效果较好。

等高线自动综合；地形结构线；Delaunay三角网；方根模型

等高线是表示地貌形态最理想、最科学的方法，对等高线图形的综合即可完成对其所表示地貌形态的综合[1]。等高线自动综合是空间数据多尺度表达的重要内容之一，由于等高线具有复杂、多样、密集等特点，使得对等高线的自动综合成为多尺度表达的瓶颈之一。国内外许多学者对等高线自动综合进行了研究，已有不少研究成果，主要有单条等高线化简综合法、基于分形分析的曲线自动综合法、等高线结构综合法和基于地貌高程带的地貌形态自动综合[2]。

“地形结构线的提取困难，但其结构化更困难”[2]，基于此观点，本文在已有研究基础上，采用一种新的提取地形结构线的方法，解决了地形结构线提取困难的问题，并将地形结构线组织成树结构。在综合等高线时运用方根模型控制谷地选取的数量指标，采用了一种新的模型来评价谷地的质量选取指标，并结合地性线树结构，完成等高线的自动综合。该方法不仅充分顾及了地貌的形态特征，避免了相邻等高线相交问题，而且在改变参数的情况下同样能适应不同形态特征的地貌类型。

1 地形特征线的提取

1.1 原始等高线数据预处理

联合Delaunay三角网模型能够探测和分析等高线成组曲线的弯曲[3]。该模型与传统Delaunay三角网模型不同的是，它首先对每条等高线单独构成 Delaunay三角网[10]，并删除各等高线所构成三角网中相交的三角形，然后再重新进行三角剖分。由此避免了相邻等高线点的干扰，能很好地探测和提取出成组曲线的弯曲。

对于一幅原始等高线数据，联合Delaunay三角网模型能最大程度的提取出成组等高线的弯曲，然而由于等高线是由一系列离散的特征点连接而成的，由于离散点分布疏密程度不一致，所以在相邻等高线的影响下，导致了少数弯曲提取不出，进而影响局部地形结构线在连接生成结构线树时中断，如图1所示。因此需要对原始等高线进行插值预处理，插值条件满足：

1)拐点A处夹角小于某一给定阈值；

2)拐点A与相邻两点B、C的距离差值大于某一给定阈值；

以上条件是在对大量原始等高线数据进行统计分析后得出的结论，若满足上述条件，则

在距离较长的AC边插入一点D，D点到拐点A的距离AD等于AB。以插值后的等高线数据构网，就能提取出完整的地形结构线，如图 2所示。插值点并非地形特征点，插值的目的在于更完整地找出成组等高线的弯曲部分，有利于地形线的完整性连接，因此在对等高线进行形状化简时，插值点均不保留，所以不会因为等高线的插值而增大数据量。

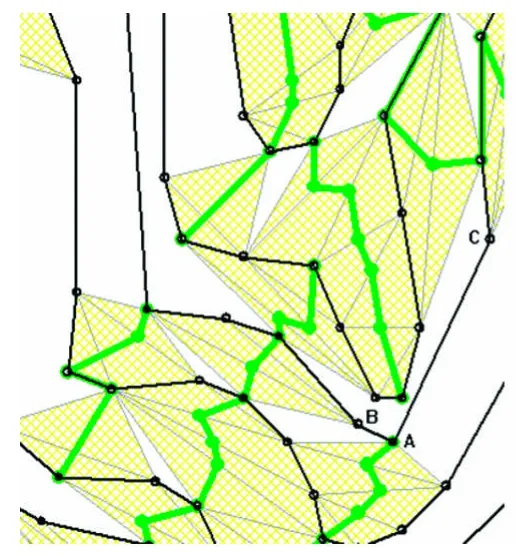
图1 原始等高线数据地形线连接中断

图2 等高线插值后地形线连接完整

1.2 地形特征线的提取及连接组织

联合Delaunay三角网构建完后，探测出每个弯曲处的平三角形区[3]，通过三角形分类处理得到整个平三角形区的中轴线[4]，以此中轴线作为近似的地形结构线树，建立局部二叉树结构[5-8]。最后采用“三角形局域连接方法”[3]连接局部地形特征线树[9,11,12]，该方法基于三角形三个顶点邻近的原理，能适应不同的地貌类型，地形线连接后的效果如图3所示。

2 等高线综合

等高线是表达地貌形态最主要的方法。由于对等高线的认识不同，历史上曾产生过关于地貌表达的两个学派：几何学派和地势学派[1]。大多数学者同意地势学派的观点，主张把地貌形态的塑造放在第一位。因此在综合等高线时，需要考虑到地貌形态类型、成组的表示、成组的理解和成组的综合等高线。

图3 联合Delaunay三角网提取的地形结构线

2.1 谷地选取数量指标

谷地的选取主要由数量指标和质量指标确定。数量指标主要用于控制谷地选取的数量，以反映不同地区地貌水平切割密度的对比；质量指标是指谷地在表达地貌中的作用，主要用于控制谷地选取的对象。

根据对不同比例尺地图进行统计分析，相邻比例尺的地图上谷地数量将构成某种比例关系。开方根规律公式可用于计算谷地选取数量[1]，计算公式为：

其中，NB为综合后图上谷地选取条数，NA为综合前图上谷地条数，MA为综合前地图比例尺分母，MB为综合后地图比例尺分母。x为选取指数，由不同的切割密度条件确定，x分别取 0，1，2，3，相应于谷地的极稀区、稀疏区、中等密度区和稠密区。

2.2 谷地选取质量指标

谷地选取的质量指标，即根据谷地的重要性来确定选取哪些谷地。重要谷地主要有以下几种[1]：

1）主河源的谷地；

2）有河流的谷地；

3）主要鞍部的谷地；

4）构成汇水地形的谷地；

5）反映山脊形状和走向的谷地；

6）较长的谷地。

然而，由于地貌形态的复杂多样性，以及确定谷地重要程度的指标也具有多样性，所以用计算机自动判断出重要的谷地是相当困难的。由此本文采用了三个指标来评价谷地的重要性：

1）地性线的长度，如图4所示，地性线AB的长度；

其中，n为地性线经过的一组等高线的条数；

图4 经过某谷地的地性线AB

3）成组等高线弯曲的平均面积S：

其中，S为地性线经过的平三角形区的总面积，n为地性线经过的一组等高线的条数。

各评价指标对谷地选取的影响程度不一样，这里采用对影响因素分配以不同的权重，利用加权值来计算谷地的重要性。具体公式如下：

其中，Q1、Q2和Q3分别为地形线长度、成组等高线弯曲的平均地性线长度和成组等高线弯曲的平均面积的权重，权值由统计分析获得。

2.3 等高线的形状化简

地貌的形状化简遵循以下两条基本原则：

1）以正向形态为主的地貌，扩大正向形态，减少负向形态[1]；

2）以负向形态为主的地貌，扩大负向形态，减少正向形态。

分别计算出各山脊线所经过的平三角形区的总面积S1和各山谷线所经过的平三角形区的总面积S2，以此作为判断地貌形态是以正向形态为主还是以负向形态为主的依据。若S1大于S2，则地貌形态以正向形态为主；反之，则以负向形态为主。这里给出地貌形态以正向形态为主化简方法。

以正向形态为主的地貌，删除谷地，合并山脊，使山体轮廓逐渐完整起来。因此在确定了谷地选取的数量指标之后，计算出各谷地的重要性，根据重要性的排序选取重要性大的谷地，剩余的即为需要被综合掉的谷地。

地貌综合结果填补山谷或削平山脊,在不同尺度下保持地貌形态,在图上综合效果则表现为删除面,如图5所示，与山谷线AB相邻的两条山脊线CD和EF,其围成的面CAEFBD就是要被综合掉的山谷.将DCFE面内等高线上的所有点删除即化简了等高线,同时保持了地貌总体形态.联合Delaunay三角网模型的优点不仅能最大程度提取出等高线群的弯曲，还在于等高线化简时控制相邻等高线不会相交。

3 实验和结论

本文针对某地1：50000地形图局部，进行了综合实验，如图 5所示。该局部地形以正向地貌为主，因此只综合掉山谷，扩大了正向地貌形态，减少了负向地貌形态。构成山谷的等高线成组的被删除，保持了等高线之间的协调关系，相邻等高线不会产生相交，综合效果较好。运用该方法综合地貌，对于平原和丘陵地区综合效果不是很理想，对此还需要做进一步的研究。

图5 基于斜面组的等高线化简

[1] 王家耀.普通地图制图综合原理[M].北京：测绘出版社，1992

[2] 吴艳兰.地貌三维综合的地图代数模型和方法研究[D].武汉：武汉大学，2004

[3] 粟卫民.基于等高线的地形特征自动提取研究[D].武汉：武汉大学，2005

[4] 乔庆华，吴凡.河流中轴线提取方法研究[J].测绘通报,2004，5：14-17

[5] 艾廷华，祝国瑞，张根寿.基于Delaunay三角网模型的等高线地形特征提取及谷地树结构化组织[J].遥感学报，2003，7（4）：292-299

[6] 毛可标，陈向东.地形结构线自动生成方法研究[J].测绘科学，1995，3：12-18

[7] 王耀革，王玉海.基于等高线数据的地性线追踪技术研究[J].测绘工程，2002，11（3）：42-44

[8] 艾廷华，郭仁忠，刘耀林.曲线弯曲深度层次结构的二叉树表达[J].测绘学报，2001，30（4）：343-348

[9] 汝绪伟.基于等高线数据的地形特征线提取及地形建模研究[D].山东：山东科技大学，2004

[10]陈仁喜，龙毅.顾及三角形处理的TIN建立算法[J].武汉大学学报:信息科学版，2003，28（5）：619-622

[11]朱庆，赵杰，钟正,等.基于规则格网DEM的地形特征提取算法[J].测绘学报，2004，33（1）：77-82

[12]王涛.地貌信息提取中结构化问题研究[D].武汉：武汉大学，2005

Research on Contour Group Generalization Based on United-Delaunay-Triangulation Model

YANG Yingwei1,LUO Juan2
(1.Chongqing Cybercity Sci-tech Company,Chongqing 400020,China;2.Chongqing Construction Management Comm ittee of New Eastern City(Yuzui Group),Chongqing 401133,China)

Extracts curves of groups of contours using"United-Delaunay-Triangulation model"(UDT in brief).At thesecurves,joinsthe local topgraphic structures by"Flat-Triangle-Jion-Method", and buildsthe"Tree Form Structure" of topgraphic structures.Using"Square Root Model"to determine the quantitative indicator of valley-selection,proposed a new mathematic model to determine the quality indicator of valley-selection,complete the contour automated generalization.Research and experimentsshow thatthismethod fully takes into account the geomorphic characteristics, valley selection is reasonable,simplification degree is appropriate, and completely avoid the intersection of adjacent contours.The generaliation result is satisfactory.

contour automated generalization;topgraphic structure;delaunay triangulation;square root model

2009-07-07

项目来源：国家基础测绘科技计划资助项目 (1469990324231)；国家自然科学基金资助项目（40571135）。

P208

B

1672-4623(2010)02-0034-03

杨英伟,工程师，从事WebGIS、地理信息多尺度表达研究。