预测蛋白质折叠结构的剪枝算法
陈昊,王代萍
(1.湖北大学 数学与计算机科学学院,湖北 武汉 430062;2.湖北大学 知行学院,湖北 武汉 430011)
0 引言
蛋白质折叠结构问题是生物信息学领域的核心问题之一.目前确定蛋白质折叠结构的一种途径是通过物理化学的方法直接观测,这种途径能较容易测出蛋白质链构成,但要观测蛋白质的空间结构却十分困难.随着计算机科学技术的进步,人们开始寻求理论计算的方法直接预测蛋白质的空间折叠结构.
针对蛋白质折叠结构,近年来科学家提出了一些简化模型,目前国际上研究最为广泛的是Dill和他的合作者提出的二维HP(hydrophobic-hydrophilic)格点模型[1].尽管蛋白质由20类氨基酸组成,但根据每类氨基酸的亲水疏水特性的不同,分为两大类,一类是疏水氨基酸(用H表示),一类是亲水氨基酸(用P表示),因此任意的蛋白质链可表示为{H,P}上一个有限长的字符串,为表述方便,将P称为白球,H称为黑球,球的直径均为1.一个合法的蛋白质空间构形必须满足以下三个约束条件:
①序列中每个小球的球心必须摆放在二维欧氏空间整数坐标上.
②任意两个在链上相邻的小球摆放后必须在二维空间上也相邻,即编号相邻小球球心距离为1.
③二维空间上的每个整数格点至多只能摆放一个小球,即任意两个小球都不能重叠.
满足以上三个条件的蛋白质折叠结构称为一个合法构形.任意合法构形都有其能量.能量定义只考虑疏水作用力,每一对在序列中不相邻而在二维空间中相邻的黑球产生能量为-1,其它情况能量计为0,计算合法构形中所有序列不相邻而物理位置相邻的H对的能量之和即是整个构形能量.一个链长为N的蛋白质合法构形能量E的形式化描述如下:

预测蛋白质折叠结构问题就是给定任意的氨基酸序列,找出满足3个约束条件的最低能量构形.例如图1是一个链长为20的蛋白质最优能量构形(图中黑色方块表示亲水氨基酸H,白色方块表示疏水氨基酸P),能量为-9.二维格点模型是一种简化模型,但这种简化模型在一定程度上反映了蛋白质系统的一些基本特征,主要考虑了氨基酸的亲水和疏水作用力,以最小能量作为优化指标,且该模型已被证实对预测蛋白质α螺旋结构有极高的可信度[2].

图1 蛋白质构形(N=20,E=-9)
文献[3]已证明基于HP格点模型的蛋白质折叠问题求解是NP难度的,因此依HP格点模型的求解蛋白质折叠问题大都寻求启发式搜索算法.目前已提出的著名的近似算法有:基于重要性抽样的SISPER算法[4];基于Monte Carlo的MSOE算法[5];基于蚁群优化思想的New ACO算法[6];基于裁减复制策略的PERM算法[7-8];基于模拟退火思想的SA算法[9].其中PERM算法是在目前公开发表的文献中依据格点模型求解蛋白质折叠问题效率最高的近似求解算法,本文在PERM算法基础上,结合拟物拟人思想,重新定义了权重、权重预测值和上下门限,得到了一种新的基于剪枝策略的启发式搜索算法.
1 基于剪枝策略的启发式搜索算法

图2 剪枝策略示意图
1.1剪枝算法(pruning algorithm)总体思想框架依据二维格点模型,可以将长度为N的蛋白质折叠构形生成过程理解为蛋白质链逐渐生长的过程.具体操作如下:考虑到空间对称性,可先将第一,二号球固定,然后在第二号球周围合法位置上放置第三号球,再在第三号球周围合法位置上放置第四号球,依次类推,逐一放置黑白球直至放完N个球.可以用一棵搜索树描述蛋白质构形的生成过程,由于从第三号小球开始,每个小球至多有3个合法的生长方向,因此一棵蛋白质折叠构形完全搜索树的叶子结点个数大约为3N-2,显然搜索空间随链长的增加成指数级增长.
剪枝算法总体思想是控制分支繁殖的规模,只对有潜力的分支进行繁殖.具体是通过制定一定的评判准则,让那些有前途的个体得以繁衍,而不具备发展前景的个体终止繁殖,从而有效地模拟了生物繁殖过程中优胜劣汰的自然规律,如图2所示.对个体的评判准则可以理解为剪枝策略,如何制定合适的剪枝策略直接决定了算法的执行效率.
1.2剪枝算法PA中的主要术语为便于描述剪枝算法,先给出算法中几个主要术语的定义.

图3 6个球的格局
定义1 格局:已放入前n(2≤n≤N)个球时蛋白质链所处的状态称为一个格局,并且将含有n个球的格局简称为格局n.如图3,称为格局6.
定义2 自由度:对于格局n,当第n+1个球放入时,其所有的合法位置数目称为格局n的自由度,记作kfree.例如图3中的格局6的kfree=3.
定义3 权重:对于格局n,其优劣程度称为该格局的权重,记作Wn.剪枝算法中对权重的采用如下递归定义:
(1)
其中,ΔEn为第n个球放入后新增的能量值;T为温度常数,一般取值范围为T∈[0.2,0.4].上述Wn实际上是表达前n个球所组成的部分链构形的能量值.
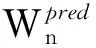

(2)
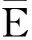
1.3剪枝算法PA描述以上分析可以看出链长为N的蛋白质构形生长过程对应于剪枝搜索树的生成过程,要描述剪枝算法只需给出如何从任一格局n-1(2≤n-1≤N-1),通过选择分支将第n个球放下,从而发展出若干新格局n.
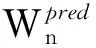

(3)~(5)
其中C>、C<为(0,1)中的常数,Zn为所有已产生格局n的权重Wn算术平均值.用Cn表示算法运行到某一时刻所有长度为n的格局的个数,则在计算过程中每得出一个新的格局,都需依据其权重Wn更新Zn和Cn,Zn⟸(CnZn+Wn)/(Cn+1),Cn⟸Cn+1.
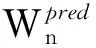
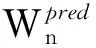

剪枝算法运行时,需首先给Zn和Cn赋初始值,一般可随机生成一个链长为N的合法构形,计算相应的Wn(1≤n≤N),则Zn和Cn可初始化为Z1=W1,…,Zn=WN;C1=C2=…=CN=1,然后采用深度优先方式递归生成剪枝搜索树,最后在所有生成的长度为N的构形中找出能量最低构形作为算法的最终输出.
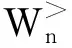
由于权重Wn直接决定了繁殖门限的大小,因此权重Wn是引导算法走向最优解的实质因素,考虑到构形能量大小是格点模型的唯一优化指标,剪枝算法中按公式(1)定义的权重Wn只与前n个球构成的部分链构形的能量值有关,这一权重的引导使得算法更加趋于问题的本质.
2 计算结果与分析
2.1实验结果用VC语言实现了剪枝算法PA,并对表1中列举的10个典型算例进行了实算,该组算例是当今国际文献中预测蛋白质折叠结构问题的公认算例.剪枝算法PA运行环境为Celeron 1.3 GHzCPU,512 M内存微型机.其他算法实验环境分别是:MSOE使用的是500 MHz Dec21164A Chip机器,SISPER使用的是 600 MHz Sony VAIO laptop机器,New ACO使用的机器是1 GHz CPU,PERM算例8使用的机器是Sun Ultra 1,算例9、10使用的机器是500 MHz Dec21164A,可以看出运行5个算法的硬件性能相当.

图4 N=64,E=-42
国际上具有代表性的4个算法以及剪枝算法均在较短时间得到了链长N<64的算例的最优构形,因此本文只对当今公认的3个典型难例进行比较,计算结果如表2所示.从计算结果的质量相比较,只有PA和PERM找到了所有算例的最低能量构形,而MOSE、SISPER和NEW ACO未能计算出部分算例的最优构形.从计算时间效率比较,PA算法总体优于PERM,尤其对于链8,PA计算速度比PERM算法快90余倍.
以链8(N=64,E=-42)为例,该算例虽然链长不算太长,但是公认的难例,尤其对生长型算法.主要表现在该链的最优构形在生长的初期能量减少较慢,直到后期才减少较多能量.剪枝算法中诸参数取值:T=0.2,C>=0.01,C<=0.2.算法运行了93 min结束共找到了5个最低能量构形,平均18.6 min找到一个最优构形,如图4所示,运行效率明显优于PERM、MSOE和New ACO,SISPER则未能找到最低能量构形.

表1 国际公认算例
E*指目前已发现的最低能量值

表2 计算结果
①②③:计算时间指算法运行过程中首次出现表中所得到能量构形的运算时间,
④⑤:计算时间指平均得到一个最低能量构形所用的时间,--表示未报道运算时间.
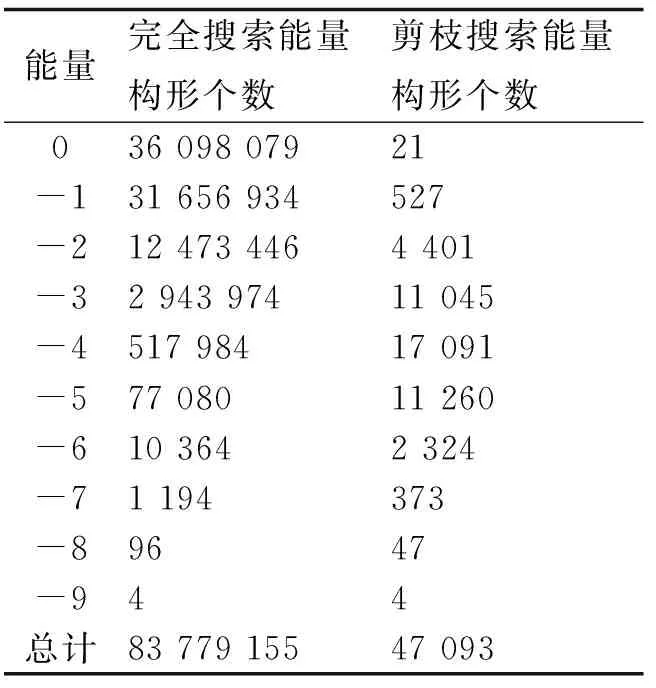
表3 剪枝算法得到的能量分布
2.2剪枝算法PA特征分析PA是一种近似求解算法,通过对一棵完全搜索树的部分分支进行剪枝从而使得算法时间复杂度降为多项式时间.表3以算例1(N=20,E=-9)为例,比较了完全搜索与剪枝算法的搜索空间大小,可以看出对于算例1剪枝算法搜索空间大小不到完全搜索空间大小的万分之六.随着链长的增长,剪枝算法搜索空间所占完全搜索空间的比重将越来越小.
同时我们发现剪枝算法中参数C>、C<的设定对算法运行效率有较大的影响,参数的设定需综合考虑解的质量和运算时间.一般而言,参数设定较大,则算法运算时间较短,但却很难找到最优解;参数设定较小,则解的质量一般很好,但算法运算时间较长.
3 结论
预测蛋白质折叠结构问题的HP格点模型是一个典型的NP难问题.目前求解该类问题大都采用一些通用的启发式搜索算法,如局部搜索、遗传算法、蚁群算法、退火算法等,但随着问题规模增大,计算优度和效率都会明显下降.本文学习了PERM算法中的剪枝思想,通过定义全新的权重、上下门限制定了一套符合自然界优胜劣汰规律的剪枝算法,实验结果表明剪枝算法是高效的,对目前公认算例组中最难的3个算例,剪枝算法均在较短时间内找到了当前已知的最低能量构形.同时剪枝算法还为求解NP难问题提供了一种新的思路,尤其对于离散空间中NP难度的搜索问题更是有很好的借鉴作用.
参考文献:
[1] Dill K A,Bromberg S,Yue K. Principles of protein folding:a perspective from simple exact models [J]. Protein Science,1995(4):561-602.
[2] Shih C T,Su Z Y,Gwan J F. The HP model,designability,and alpha:helices in protein structures[J]. Physical Review Letter,2000,84:384-389.
[3] Berger B,Leighton T. Protein folding in the hydrophobic-hydrophilic(HP) model is NP complete[J]. Journal of Computational Biology,1998,5(1):27-40.
[4] Junni L Z,Jun S L. A new sequential importance sampling method and its application to the two-dimensional hydrophobic:hydrophilic Model[J]. Journal of Chemical Physics,2002,117(7):3492-3498.
[5] Chikenji G,Kikuchi M,Iba Y. Mutlti-self-overlap ensemble for protein folding:ground state search and thermodynamics[J]. Physical Review Letter,1999,83(9):1886-1889.
[6] Shmygelska A,Hoos H H. An improved ant colony optimization algorithm for the 2D HP protein folding problem[M]//Canadian Conference on AI,Lecture Notes in Computer Science. Berlin:Springer Verlag,2003:2671-2683.
[7] Hsu H P,Mehra V,Nadler W,et al. Growth algorithms for lattice heteropolymers at low temperatures[J]. Journal of Chemical Physics,2003,118(1):444-452.
[8] Hsu H P,Mehra V,Nadler W,et al. A growth-based optimization algorithm for lattice heteropolymers [J]. Physical Review E,2003,68(2):1007-1011.
[9] 陈矛,黄文奇,吕志鹏.求解蛋白质折叠问题的模拟退火算法[J].小型微型计算机系统,2007,28(1):75-78.

