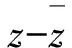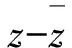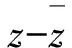强调感性 结合理性 背景新颖——2010年数学高考有关合情推理与数系扩充的试题评析

● (绿城育华学校 浙江杭州 310012)

合情推理和数系扩充作为高考中不算是重点内容，但又是数学高考的内容之一，历来不是备考的重点复习对象，学生花的时间非常少.但是，合情推理在培养学生的数学素养及数学思维能力方面有着不可替代的作用，复数知识是整个数学知识体系中不可缺少的一部分，是未来学习高等数学的基础知识之一.

1 合情推理

1.1 试题分析

合情推理是波利亚“启发法”中的一个推理模式，在解题中表现为归纳推理和类比推理.通过找出处理各类问题所共有的一般特征，在没有现成的解题方法时寻求一条绕过障碍的道路,达到所要去的而不能立即达到的目的.

2010年的大纲对合情推理和演绎推理的要求没有变化，但是由于合情推理在数学发现中的作用以及在培养学生发现问题和创新意识中的重要作用，新课程在继续强调演绎推理重要性的同时，同样注重合情推理在解题中的运用.

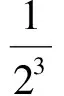
其中Tn=________.

(2010年浙江省数学高考理科试题)

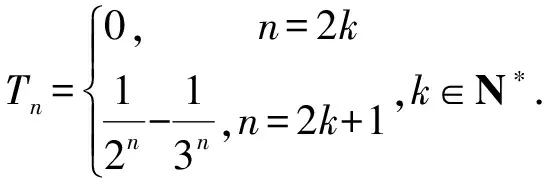
此题考查的是归纳推理的思想方法，并参入了简单的分类讨论.与2009年比较，难度有些降低.

例2若数列{an}满足：对任意的n∈N*，只有有限个正整数m使得am

(2010年湖南省数学高考理科试题)

答案2，n2.

此题以数列知识为背景，通过新定义的运用考查学生的自学能力、探究推理能力及创新能力，难度较大.

推理作为一种思想方法蕴藏在数学知识的发现过程中，考查的是学生的观察、分析、比较、归纳等能力，强调感性和理性的结合，数学直觉和逻辑推理的结合.它的题型往往是结合其他数学知识特别是数列知识，因而在学习中应该将推理论证贯穿于整个学习当中.

1.2 教学建议

这2年考查合情推理的题型都是以填空题的形式出现，估计暂时不会有什么变化，但是绝不能因为这2年考的是归纳推理而重“归纳”、轻“类比”.事实上，类比推理能够让问题的解决跨越知识的界限，对锻炼学生的思维及将已有的知识运用到新的问题中去具有很好的作用.

合情推理的相关专题较少，学生用以训练的机会很少，这需要教师在平时教学中注意合情推理的运用.例如在数列的教学中，可利用归纳推理推导等差数列的相关公式，再通过演绎推理来论证，最后利用类比推理得到等比数列的相关公式并加以证明验证.

2 复数系

2.1 试题分析

2010年的文、理科复数试题大部分依然是考查复数的概念及四则运算，而运算中以复数的乘法和除法为考查的重点.

2010年的浙江卷理科复数试题难度和深度超过全国其他省份，并和2009年有了明显的不同.2009年的复数题考查复数的四则运算，充分考查的是复数的加、乘和除综合运算.而2010年的试题考查角度从往年的代数角度转到了几何角度，考查复数的模及复数系的概念.

例3对任意复数z=x+yi(x,y∈R)，i为虚数单位，则下列结论正确的是

( )

(2010年浙江省数学高考理科试题)

本题主要考查了复数的四则运算、共轭复数及其几何意义，属中档题.

此题可借助于复数坐标系来解.特别对于稍难的选项D，利用图形可直观地得到结果，再一次体现了数形结合思想的运用价值，而直角坐标系和向量坐标系与复数坐标系的通性亦体现了数学知识中的通性通法.

2.2 教学建议

很多教师认为复数试题考查的都是运算问题，而忽略了对复数知识体系的全方位了解及其体现的价值.复数知识引入虚数概念，并完善了复数的加减乘除的运算，使复数知识自圆其说，构成一个完整的体系，它和当年向量概念的引入和知识的扩展是非常相似的.对复数系和直角坐标系、向量坐标系的共同或相似之处缺乏对比，使复数知识显得相对孤立，从而使学生在学习时往往是以记忆为主，而没有去理解复数知识引入的价值，缺乏对复数知识体系的完整了解.因此在教学中,需引起教师的关注.