基于分数阶傅里叶变换的变频调速异步电机故障诊断方法*

张雄希，刘振兴

(1.武汉科技大学冶金自动化与检测技术教育部工程研究中心，湖北武汉 430081;2.武汉科技大学信息科学与工程学院，湖北武汉 430081)

0 引言

在传动领域，变频调速异步电机驱动系统应用越来越广泛。由于频繁起停、过载、电源冲击等原因可对驱动系统造成异常和故障。尤其是数字化调速系统的大量引入，电动机经常处于调速状态，供电电源不再是理想的正弦波分布，电源波形会发生畸变，产生大量的谐波，附加损耗和冲击型电源会损伤定、转子绕组和铁心。因此，需要对其进行有效的状态监测与故障诊断，以利生产顺利地进行。

1 变频调速异步电机驱动系统特性

变频调速系统中的变频电源采用了整流、逆变和高频开关等电力电子元件，使输出电压中的谐波成分剧增，系统具有高度的非线性特性，输出电压波形的变化陡度比工频电压大得多。若有断条等故障发生，由于变频电源谐波影响，定子电流

频谱中的基波旁瓣更易于湮没故障特征频率，同时由于运行过程中变频器输出电压的大小、频率、功率开关器件的触发角度均与运行模式有关，使得采用一般频谱分析方法难以有效地提取故障特征，实现准确的故障诊断。因此，变频调速异步电机的故障诊断方法需另辟蹊径。

2 分数阶傅里叶变换定义及特点

分数阶傅里叶变换是近年发展起来的一种新的时频分析工具，它是傅里叶变换的广义形式。从本质上讲，信号在分数阶傅里叶域上的表示，同时融合了信号在时域和频域的信息。它已被广泛应用于光学系统分析、滤波器设计、信号分析、解微分方程、相位恢复、模式识别等领域。

借用时频分析的概念，以时间和频率分别为横轴和纵轴，则可把普通的傅里叶变换X(f)看作是时间信号x(t)逆时针旋转π/2的线性变换，即Rπ/2=F。如果角度α不等于π/2整数倍旋转，时间信号x(t)逆时针旋转π/2的非整数倍的线性变换，可称作分数阶傅里叶变换。

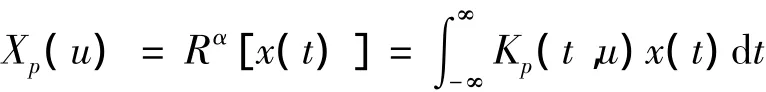
式中变换核取作:

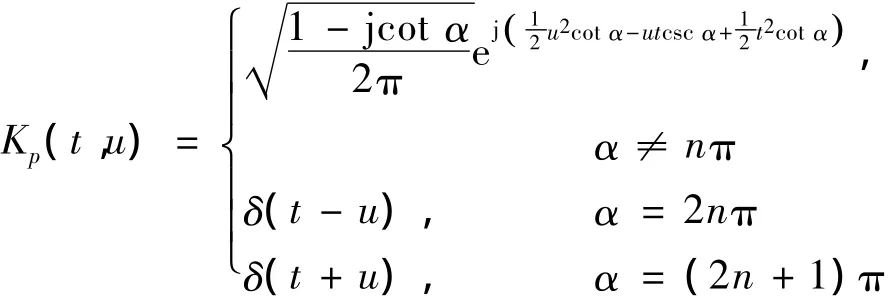
式中:n为整数，α=pπ/2，p称为分数阶傅里叶变换的阶数，Xp(u)称为x(t)的p阶傅里叶变换。

分数阶傅里叶变换具有时移特性、频移特性及尺度特性等性质。利用分数阶傅里叶变换，通过改变阶次p，可自动调节时域和频域分辨率。因此，该方法具有良好的时频局部化特性，对于时变信号处理和特征提取具有独特的优越性。

3 基于分数阶傅里叶变换的变频调速异步电机断条故障诊断方法

本文讨论的变频调速系统中变频器为交－直－交电压型。交－直－交变频器主要由整流部分(D1—D6)、整流电容C和逆变部分(T1—T6)组成，如图1所示。

图1 异步电机变频调速系统示意图

根据故障统计结果，本文对变频调速异步电机的主要故障异常行为——转子断条的特征及诊断进行研究。根据多回路模型与参数建立正常和断条时的电动机数学模型，再根据正弦脉宽调制(SPWM)理论建立逆变器模型，并分析其对电动机的谐波影响。

3.1 基于分数阶傅里叶变换的变频调速系统运行模式确定

多数变频调速系统经常处于动态调速过程中，其运行模式可分为:匀速、恒加速、恒减速或其他方式。匀速运行状态下变频器的输出基波电压大小和频率恒定;额定频率以下的恒加速情况下，电压和频率按照如下规律变化:

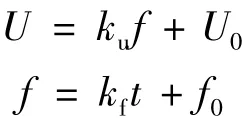
式中:U0——低频情况下的补偿电压值;

ku——电压随频率变化的比例;

kf——频率随时间变化的比例;

f0——初始变化频率。

额定转速以上电压不变，只变频率。图2中曲线1代表匀速运行，曲线2代表恒加速运行，恒减速运行可以相应处理。

对于变频调速异步电机而言，运行模式的确定是诊断的关键问题之一，如何提取变频器电压频率变化规律显得非常重要。在恒速运行情况下，基波频率为固定值，使用常规的频谱分析方法可有效地解析。但在恒加速(恒减速)情况下，基波频率随时间按线性规律变化(见图2中直线2)，近似为线性调频(LFM)信号。常规的频谱分析方法无法有效的对其解析，使用分数阶傅里叶变换可以解决此问题。

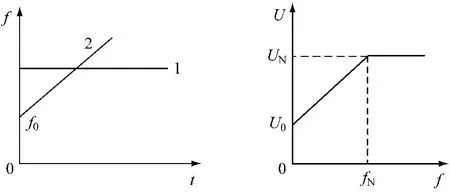
图2 恒速和加速情况下频率、电压的变化规律

分数阶傅里叶变换可将待分析信号的时频结构按一定角度进行旋转。因此，一个线调频信号在适当的分数阶域中将表现为一个冲激函数，即分数阶傅里叶变换在某个特定的分数阶傅里叶域中对给定的LFM信号具有最好的能量聚集性。通过选择合适的角度(g0=－cot α)，即选择角度与信号匹配，就可以得到一个冲击信号，其能量在分数阶域u轴的对应点聚集。因此，可根据LFM信号在某一分数阶傅里叶域的聚集性来检测和识别LFM信号。

如图3所示，恒速运行情况下，基波频率为固定值，在时间－频率平面上，为一条与横坐标平行的直线，与横坐标之间夹角为0(见图3中直线1)，近似为正弦波;恒加速情况下，基波频率随时间按线性规律变化(见图3中直线2)，近似为LFM信号。如能检测出该直线与横坐标之间的夹角α，使时间－频率平面旋转α角度，得到新的时间－频率平面 t′-f′1，此时的频率由原来的线性变化转化成了常数，将LFM信号转化为正弦波，相当于恒定频率运行。因此，当α=0时，恒速运行;α≠0时，恒加速运行。恒加速运行时，对信号进行α角度的分数阶傅里叶变换，转化为正弦波。

当α≠0时，电机处于恒加速状态，可以通过分数阶傅里叶变换选择适当的角度α将线性变换的频率变成恒频频率，并通过tan α的正负来确定运行模式。时频夹角α与运行模式之间的关系如表1所示。

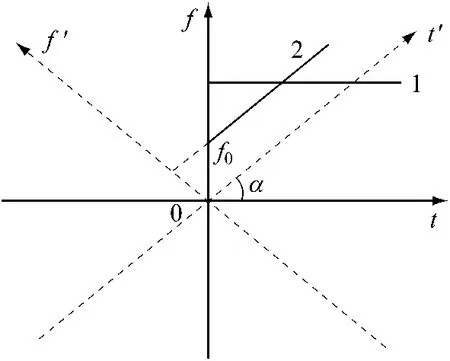
图3 频率变化规律示意图

表1 时频夹角与运行模式的关系表

根据表1可以提取定子电流或电压的频率，通过分数阶傅里叶变换确定其最佳角度α的正切值，从而确定电机运行模式。这就是分数阶傅里叶变换应用于变频调速异步电机运行模式确定的主要思想。

3.2 基于分数阶傅里叶变换的变频调速异步电机断条故障诊断方法

正弦波电源供电条件下异步电动机的常见故障特征为:定子电流中会出现频率为fb=(1±2ks)f1(其中 f1为工频，s为转差率，k=1，2，3，…)的故障特征电流。在动态变频调速过程中，供电电源的频率、电压大小均可能随时间变化，转速也相应发生变化，在变频调速异步电机存在断条故障时，定子电流中故障特征频率成分为fb=f1±2fnsn(fn为额定频率、sn为额定转差率)，其中f1=f0+kft为线性变化的变频频率。可以采用分数阶傅里叶变换对这类LFM信号进行处理。

变频调速异步电机的电源频率是近似线性变换的，基于分数阶傅里叶变换的变频调速异步电机断条故障诊断方法的中心思想就是利用分数阶傅里叶变换选择合适的角度将LFM信号变成恒频信号。变成恒频信号后用常规的傅里叶变换进行频谱分析存在的问题是:由于主频的幅度远大于故障特征频率，容易把故障频率湮没掉，可利用Relax算法消除基波和谐波影响后，通过合成Park’s矢量和瞬时功率，达到故障诊断的目的。基于分数阶傅里叶变换的变频调速异步电机断条故障诊断时的基本步骤如下:

(1)对变频调速异步电机定子电流进行分数阶傅里叶变换，获得最佳角度α，根据正切值tan α的正负来判断电机的运行模式;

(2)若为恒频恒速运行模式，则用常规的傅里叶变换进行频谱故障分析，若为恒加(减)速运行模式，则将定子电流进行分数阶傅里叶变换，获取最佳角度α，在最佳角度α下进行分数阶傅里叶变换，将LFM信号转变为恒频信号;

(3)将恒频信号进行傅里叶变换，由时域信号变换到频域，根据频域信息提取故障特征频率;

(4)利用Relax算法消除基波和谐波影响后，通过合成Park矢量和瞬时功率，频谱图上只剩下突出的故障频率特征，达到了故障诊断的目的。

4 结语

作为傅里叶变换的一种广义形式，分数阶傅里叶变换同时融合了信号在时域和频域的信息，是一种新的时频分析方法。本文根据变频调速异步电机驱动系统输出特性提出基于分数阶傅里叶变换的变频调速异步电机断条故障诊断方法，能准确地突出故障特征，处理优势明显，研究方法具有实际的工程应用价值。

[1]沈标正.电机故障诊断技术[M].北京:机械工业出版社，1996.

[2]崔博文，任章.基于Fourier交换和神经网络的逆变器故障检测与诊断[J].电工技术学报，2006，21(7):37-43.

[3]高景德.交流电机及其系统的分析[M].2版.北京:清华大学出版社，2005.

[4]尉宇.线性调频和非线性调频信号的检测与参数估计[D].中国学位论文全文数据库，2005.

[5]刘粤钳，姚红玉.分数Fourier变换在信号处理中的应用研究[J].数值计算与计算机应用，2007(9):199-201.