基于等效数值法的地下工程围岩稳定性评价研究＊

叶洲元

(1.煤矿安全开采技术湖南省重点实验室, 湖南湘潭市 411201;2.湖南科技大学能源与安全工程学院, 湖南湘潭 411201)

基于等效数值法的地下工程围岩稳定性评价研究＊

叶洲元1,2

(1.煤矿安全开采技术湖南省重点实验室, 湖南湘潭市 411201;2.湖南科技大学能源与安全工程学院, 湖南湘潭 411201)

基于等效数值原理并结合地下工程围岩本身特性,对地下工程围岩稳定性进行了评价。选取5个影响围岩稳定性的指标进行评价,分别是围岩质量指标D值、单轴抗压强度Rc、岩体完整性指标Kv、地下水渗水量W和节理状况,并把围岩稳定性等级分为5级。将该方法用于大冶铁矿一地下工程围岩的稳定性评价中,并与模糊识别法、可拓方法进行了比较。研究结果表明,等效数值法用于围岩稳定性的评价,具有识别能力强,计算简单高效的特点,便于工程应用。

围岩;稳定性;等效数值法;评价

0 引 言

地下工程围岩是指地下工程周围受开挖影响范围内的岩体,是围岩稳定性评价的研究对象[1,2]。在地下工程建设的各个阶段(规划、勘察、设计和施工)中,地下工程围岩稳定性评价是地下工程设计和制定相应工程措施的重要基础工作。但是围岩稳定性评价是一个比较复杂的问题,地下工程岩体的复杂性不仅表现在组成结构及影响因素方面,而且还表现在各因素的影响程度因不同的岩体、受力状态和运营环境而异上[3]。目前,许多研究人员针对地下工程围岩稳定性提出了很多种评价方法,例如灰色优化理论[1]、模糊识别[3,4]、可拓方法[2]、神经网络[5]、距离判别方法[6]、突变级数法[7]等。这些方法各有特点,但是由于各自方法的特点,在工程现场有时很难应用。而等效数值法不需要建立复杂的数学模型,计算简单,精确度高,工程设计人员易于掌握。因此,本文借鉴等效数值法原理,结合地下工程稳定性评价的具体特点进行了具体应用。

1 等效数值法

1.1 围岩稳定性等效数值评价法的原理

等效数值法的基本原理是:将不同性质的量纲指标化为无因次量纲的标准形式,转化后的指标值为(0,1)之间的实数,这些转化后的实数被称为“等效数值”[8,9]。

在地下工程围岩稳定性评价中,假设有m项评价指标,n个实测的围岩样本,h级围岩稳定性分级标准,则共有m×n×h个指标值Fijt(i=1,2,……,m;j=1,2,……,n;t=1,2,……,h)。采用式(1)化为等效数值。

式中:ωij为第j个围岩样本对第i个评价指标的权值,采用指标超标法根据式(3)计算:

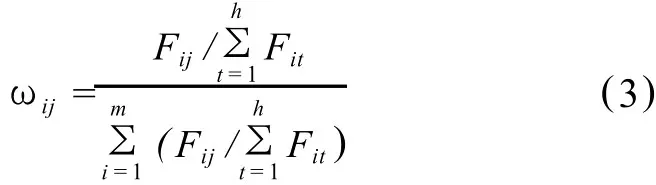
1.2 判别准则[9]

通过计算得到围岩各样本对不同稳定性等级的等效数值,之后进行评价。采用的判别准则为:对于第j个实测的围岩样本,如果Fjt为最大,则第j个围岩样本代表的围岩稳定性等级就判定为t级。

2 地下工程围岩稳定性的影响因素分析

对地下工程围岩稳定性进行分类,首先要确定影响围岩稳定性的因素,尤其是影响较大的因素。本文选取了实测岩体质量指标RQD、单轴抗压强度Rc、岩体完整性指数KKv、地下水渗水量W和节理状况等5个对围岩稳定性影响较大的因素,并将其作为评价的指标,采用5级分类,各指标的分类标准列于表1。根据5项指标,把围岩稳定性等级分为5级,即稳定(Ⅰ)、较稳定(Ⅱ)、中等稳定(Ⅲ)、不稳定(Ⅳ)和极不稳定(Ⅴ)。根据等效数值法的原理以及相关文献[2,3],得到围岩稳定性等级指标界限值(见表1)。

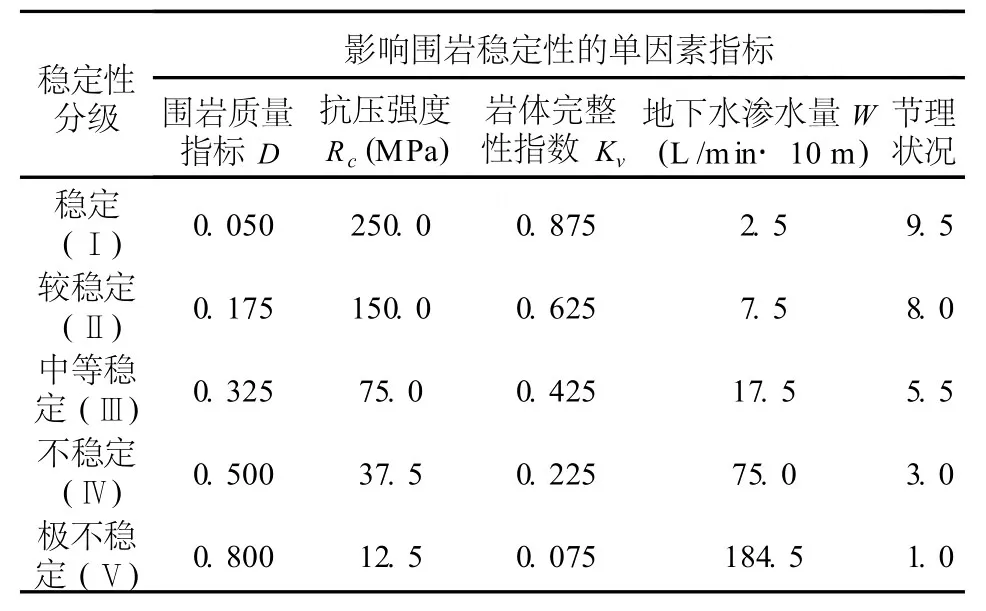
表1 围岩稳定性等级指标界限值

3 工程实际应用

大冶铁矿位于湖北省黄石市铁山区,是武钢集团公司重要的矿石基地,赋存有6大矿体。笔者利用大冶铁矿所建的一地下工程中的围岩进行等效数值法的具体应用说明。5项围岩的主要评价指标值见表2,利用等效数值法对上述5项围岩的稳定性进行评价。

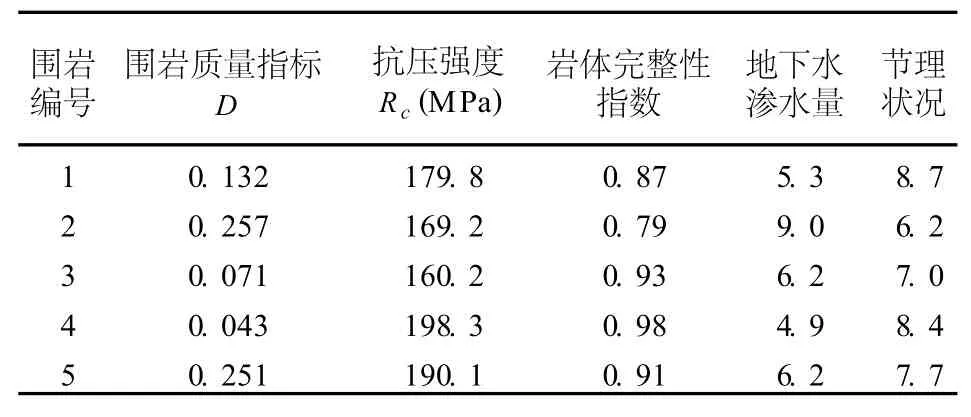
表2 大冶铁矿围岩稳定性评价指标的实测值

以1号围岩为例,首先将实测数据组成参考数列Fi1(i=1,2,……,5),即Fi1=(0.132,189.8,0.87,5.3,8.7),围岩稳定性评价标准组成被比较数列Fit(i=1,2,……,5;t=Ⅰ,Ⅱ,……,Ⅴ),即FiⅠ=(0.05,250,0.875,2.5,9.5),FiⅡ=(0.175,150,0.625,7.5,8.0),FiⅢ=(0.325,75,0.425,17.5,5.5),FiⅣ=(0.050,37.5,0.225,75,6.0),FiⅤ=(0.800,12.5,0.075,184.5,1.0)。然后根据式(1)计算得到等效数值(t=Ⅰ,Ⅱ,……,Ⅴ),即=(0.379,0.806,0.994,0.472,0.922),=(0.803,0.790,0.79118,0.773,0.920),=(0.627,0.395,0.488,0.589,0.632),=(0.576,0.198,0.259,0.518,0.345),=(0.545,0.066,0.086,0.507,0.115)。根据式(3)计算得到,ωi1=(0.106,0.226,0.278,0.132,0.258)(i=1,2,……,5)。再由式(2)计算得到综合等效数值F1t=(0.799,0.716,0.696,0.632,0.524)(t=Ⅰ,Ⅱ,……,Ⅴ)。在F1t的5个参数值中,第1个数值最大,因此1号围岩稳定性评定为稳定,即为(Ⅰ)类岩石。同理,根据等效数值法计算其他4种围岩的稳定性等级。最后得到5种围岩的综合等效数值(见表3)。为了进行比较,表3同时列出了利用模糊模式识别和可拓法的判别结果。模糊模式识别考虑各评价指标的权重,实质上是假定各指标为等权重,显然这对于各指标为不等权重的情况是不适合的。可拓方法中也存在着权重的确定问题,因此有一定的人为影响。和上述两种方法相比较,等效数值法进行计算时,可以得到唯一的结果,不受人为影响。进行计算时,可以利用excel或者matlab做成简单的数据处理软件,把实测数据代入后,很快就得到评判结果。计算过程简捷高效,适合于相关工程人员的现场应用。

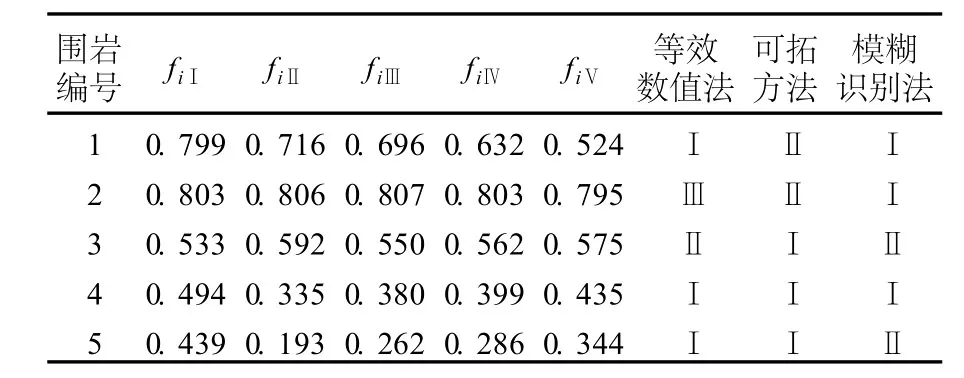
表3 综合等效数值

4 结 论

地下工程围岩稳定性的评价是一项很关键的基础工作,由于围岩介质本身的特点,导致该问题具有一定的复杂性。文中根据等效数值原理,选取了影响围岩稳定性的5项指标作为影响因素进行评价。按照围岩的稳定状况分为5类。利用等效数值法对大冶铁矿一地下工程的5项围岩稳定性进行了评价。研究结果表明,等效数值法应用于围岩稳定性的评价,具有计算简单高效,使用方便等特点,可以在实际工程中进行推广应用。

[1]冯玉国.灰色优化理论模型在地下工程围岩稳定性分类中的应用[J].岩土工程学报,1996,18(3):62～66.

[2]连建发,慎乃齐,张杰坤.基于可拓方法的地下工程围岩评价研究[J].岩石力学与工程学报,2004,23(9):1450～1453.

[3]许传华,任青文.地下工程围岩稳定性的模糊综合评判法[J].岩石力学与工程学报,2004,23(11):1852～1855.

[4]彭振华.锦州天桥LPG洞库场地岩体质量评价研究[D].北京:中国地质大学,2002.

[5]杨朝晖,刘浩吾.地下工程围岩稳定性分类的人工神经网络模型[J].四川联合大学学报,1999,3(4):66～72.

[6]宫凤强,李夕兵.距离判别分析法在岩体质量等级分类中的应用[J].岩石力学与工程学报,2007,26(1):190～194.

[7]宫凤强,李夕兵,高 科.地下工程围岩稳定性分类的突变级数法研究[J].中南大学学报,2008,39(5):1081～1087.

[8]李明山.等效数值法在地下水环境质量评价中的应用[J].工程勘察,1998,(6):36～38.

[9]张晓炜,杨 涛,巩 安.路基膨胀土胀缩等级的等效数值评判法[J].公路,2000,(10):65～66.

湖南省教育厅项目(06C320).

2010-02-06)

叶洲元(1977-),男,湖北蕲春人,博士研究生,讲师,主要从事矿山工程与爆破等研究,Email:yezhouyuan@126.com。