500 kV同塔双回输电线路绕击跳闸率的计算分析

刘晓冬，苏红梅，徐茂文，郑雄伟

(1.河北省电力研究院，石家庄 050021；2.石家庄供电公司，石家庄 050051)

1 概述

随着我国经济高速发展，全国电网加快改建，大城市、工农业发达区域、林区等地区的线路走廊越来越紧张，而且线路走廊用地费用日益昂贵，因此在我国超高压输电线路通常采用“同塔双回”架线模式，这样可减少500 kV输电走廊占地，降低线路建设投资。

根据我国华东、华北500 kV交流线路运行经验可知，输电线路90%的雷击跳闸主要由绕击引起。图1为1999-2003年广东省利用雷电定向定位仪测量的500 kV交流线路雷击跳闸的雷电流幅值分布[1]。

图1 500 kV线路雷击跳闸雷电流幅值分布

由图1可知，引起线路雷击跳闸的雷电流主要为两部分：雷电流幅值较小，在0～50 kA之间，占92.5%；雷电流幅值较大，超过160 kA，占7.5%。这是由于幅值较小的雷电流可能绕击线路导线，造成绕击跳闸；幅值较大的雷电流击中杆塔或地线，可能造成反击跳闸；中等幅值的雷电流要引起绕击跳闸其幅值太大，要引起反击跳闸其幅值又太小(接地电阻特别大的个别杆塔可能会出现例外)，因此发生绕击和反击跳闸的概率较小。

根据国家电网公司调度中心雷击跳闸的统计，截止到2006年，在运的500 kV同塔双回线路未发生过异名相同时故障，而异名相同时故障只有反击才能造成，这间接证明同塔双回线路防雷重点为防止雷电流绕击。因此，以下对东骅500 kV同塔双回输电线路的绕击跳闸率进行计算。

2 500 kV同塔双回输电线路的计算参数

东骅500 kV同塔双回输电线路的系统参数：额定电压500 kV，最高电压550 kV，系统频率50 Hz；线路全长55.5 km，导线型号为JL/LB20A-400/35，每相导线四分裂，子导线分裂间距均取450 mm；地线型号为JLB14-80。线路使用OPGW-1型光缆；铁塔选用典型直线塔SZV1B和SZV2B，绝缘子选取XP-160,28片，V型串；当地大地电阻率100 Ω·m；杆塔水平档距400 m；年平均雷电日40天；铁塔尺寸见图2。

图2 东骅500 kV同塔双回输电线路铁塔尺寸(单位：mm)

3 线路绕击计算方法的分析

我国输电线路雷电屏蔽系统设计及其性能的估算，以电力行业标准DL/T 620-1997《交流电气装置的过电压保护和绝缘配合》为依据。其绕击计算方法，没有考虑雷电绕击导线的过程、雷电流的大小和地面倾角对避雷线屏蔽效果的影响，而是根据经验和小电流试验模型提出的综合平均法，笼统地按照平原和山区2种地形分别计算绕击率，并且只考虑了保护角和杆塔高度对绕击率的影响，无法解释屏蔽失效的问题和绕击率过高的原因。

由于规程给出的算法对同塔双回线路存在不合理性，所以，电气几何模型、先导模型和分形模型成为目前线路绕击计算的几个主要模型。而建立在击距概念基础上的电气几何模型法(EGM)[2]比较细致的考虑了雷电绕击输电线路的整个过程，提出了绕击率与雷电流幅值和地面倾角等相关的观点，并能够考虑线路结构和雷电参数等对绕击率的影响，用此方法来分析雷电绕击输电线路得到的结果更接近实际情况。电气几何模型法基本概念如下。

a. 由雷云向地面发展的先导通道头部，在到达被击物体的临界击穿距离(击距)以前，击中点是不确定的，先到哪个物体的击距内，即向该物体放电。

b. 击距rs是雷电流幅值I的函数。各国采用的此函数关系不完全相同，以下研究中考虑了4种函数关系式，取其最严重者，并考虑10%误差。

c. 先导接近地面时的入射角ψ服从某一给定的概率分布函数。

以下应用电气几何模型对线路典型杆塔绕击跳闸雷电流进行计算。图3为雷击线路的电气几何模型。

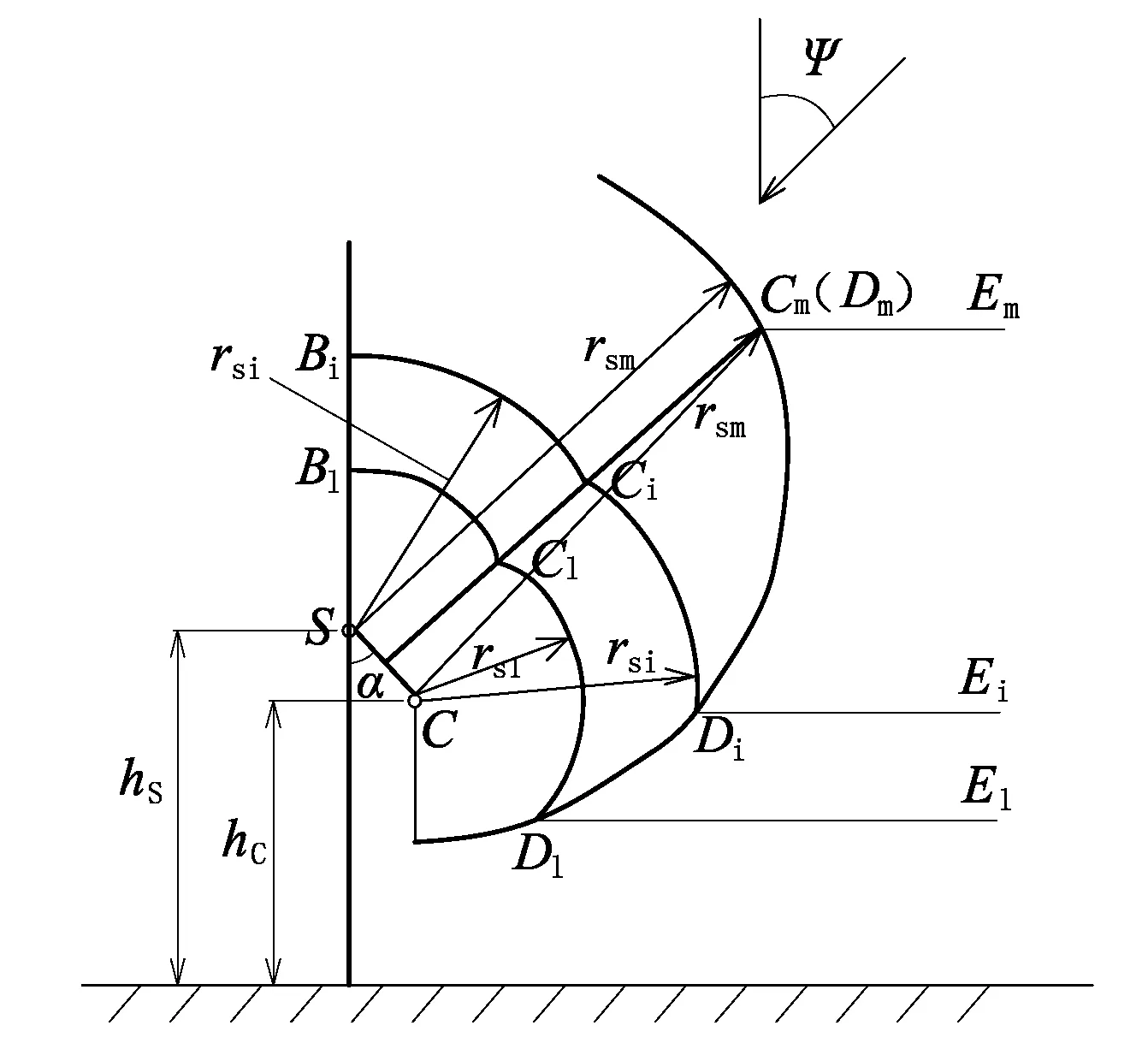
图3 雷击线路的电气几何模型

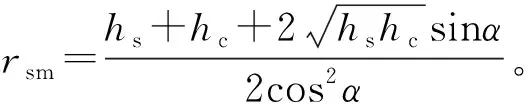
只有当雷电流在导线上引起的电压Uc(包括工作电压)大于绝缘放电电压时才会引起绝缘闪络，由此可以确定最小危险绕击电流。当地面倾斜角不为零时，其计算要复杂些[3]，但基本原理相同。

4 2种塔型绕击跳闸率的计算结果及影响因素分析

4.1 计算结果

由于东骅500 kV同塔双回输电线路上的一根避雷线要保护多根导线，因此存在雷电绕击不同导线的可能性，首先要对各导线可能的绕击范围进行分析。以 SZV1B 型杆塔为例，经过计算，可以得到各层导线的最大击距和最大绕击电流。在不同的击距系数条件下，三层导线的最大击距rsmax相差较小，因此在进行绕击跳闸率计算时，将三相导线的绕击跳闸率分别进行计算，来综合考虑东骅500 kV同塔双回输电线路的绕击耐雷性能。

根据图4电气几何模型，利用Matlab程序计算了500 kV同塔双回线路的绕击跳闸率。在仿真计算中，对于击距与雷电流幅值的关系公式，选用的是IEEE推荐的公式rs=8I0.65，对绕击跳闸率进行计算，所得绕击跳闸率的计算结果见表1、表2、表3。

表1 不同地面倾角下的绕击跳闸率 次/100 km·a

地面倾角/(°) 0°10°20°30°SZV1B型杆塔上层导线0.237 40.322 80.610 21.073 1中层导线0.276 80.383 70.737 31.333 9下层导线0.234 40.373 10.792 41.559 9SZV2B型杆塔上层导线0.408 20.508 60.845 71.389 6中层导线0.514 40.639 51.049 81.749 7下层导线0.528 40.695 91.186 12.104 2

注：击距系数k=0.8。

表2 不同保护角下的绕击跳闸率 次/100 km·a

保护角 /(°) -50510SZV1B型杆塔上层导线0.404 60.632 60.988 21.480 0中层导线0.333 20.539 00.885 01.369 2下层导线0.186 00.348 80.632 01.064 2SZV2B型杆塔上层导线0.609 40.89901.333 81.917 8中层导线0.576 40.854 81.302 01.901 4下层导线0.440 40.689 61.103 21.682 6

注：击距系数k=0.8，地面倾角为0°。

表3 不同击距系数下的绕击跳闸率 次/100 km·a

击距系数0.60.70.80.91.0SZV1B型杆塔上层导线0.505 20.356 00.237 40.145 40.077 4中层导线0.638 20.434 20.276 80.158 60.075 4下层导线0.668 20.417 00.234 40.109 40.033 8SZV2B型杆塔上层导线0.729 20.554 00.408 20.288 20.095 7中层导线0.959 60.714 60.514 40.353 40.226 4下层导线1.098 60.779 80.528 40.334 40.190 2

注：地面倾角为0°。

4.2 影响因素分析

4.2.1 杆塔高度的影响

当杆塔高度增加时，引雷面积增大，绕击跳闸率增加。计算结果表明，在地面倾角和保护角相同的条件下，绕击跳闸率随杆塔高度的增加而增大。对于呼称高度分别为42 m和48 m的SZV1B型杆塔和SZV2B型杆塔，当地面倾角为0°(平地)时，后者的绕击跳闸率为前者2.25倍；当地面倾角为20°时，后者的绕击跳闸率为前者的1.50倍。由此可见，杆塔高度对绕击跳闸率有较大影响。

4.2.2 地面倾角的影响

通过计算表明，在杆塔高度和保护角相同的条件下，绕击跳闸率随地面倾角的增加而增大。对于呼称高度为42 m的SZV1B型杆塔，在地面倾角为10°时比地面倾角为0°(平地)时绕击跳闸率增大了59.2%；地面倾角为20°比地面倾角为10°时绕击跳闸率增大了112.4.0%；而地面倾角为30°比地面倾角为20°时，绕击跳闸率增大了96.9%。由此可见，山区线路的绕击跳闸率比平原线路高。

4.2.3 保护角的影响

在杆塔高度和地面倾角相同的条件下，绕击跳闸率随保护角的增加而增大。对于呼称高度为42 m的SZV1B型杆塔，在地面倾角为0°(平地)的情况下，保护角为-5°时的绕击跳闸率比保护角为0°时减小了36.1%；保护角为0°比保护角为5°时减小了35.9%；保护角为5°比保护角为10°时减小了33.2%。由此可见，对于同杆双回输电线路，宜采用较小的保护角，甚至是负的保护角。

4.2.4 击距系数的影响

在分析500 kV同塔双回线路绕击耐雷性能时，选择合理的击距系数至关重要。在其他条件相同的情况下，击距系数k对绕击跳闸率的影响较大。随着击距系数的减小，绕击跳闸率增大很快，且当击距系数越小时，绕击跳闸率增加越快。

5 结论

a. 建立在击距概念基础上的电气几何模型法(EGM)，较细致的考虑了雷绕击输电线路的整个过程，提出了绕击率与雷电流幅值和地面倾角等相关观点，并能够考虑线路结构和雷电参数等对绕击率的影响,因此，利用该方法来分析雷电绕击输电线路得到的结果更接近实际情况。

b. 在运用电气几何模型法分析500 kV同塔双回输电线路的绕击耐雷性能时，由于杆塔较高，则击距系数对线路绕击率的影响不可忽略,因此在分析其超高压同塔双回线路的绕击耐雷性能时，应加强对击距系数的研究。

c. 对于同塔双回线路，由于一根避雷线要保护多根导线，因此宜采用较小的保护角，甚至是负的保护角，并且应在条件允许的范围内，尽量降低杆塔高度，从而提高线路的绕击耐雷性能。

d. 计算结果表明，SZV1B型杆塔防绕击跳闸性能优于SZV2B型杆塔。如果因地制宜提出适合于输电线路微观条件的防雷方案，将节省线路防雷改造花费的大量人力物力，起到事半功倍的作用。

参考文献：

[1] 古定燮，樊灵孟. 对我国500 kV线路防雷的新思考[J]. 中国电力，2004，37(12)：18-21.

[2] 张纬钹，何金良，高玉明. 过电压保护及绝缘配合[M].北京:清华大学出版社，2002.

[3] 李如虎.地面坡度对高压输电线路绕击率的影响[J].高电压技术，2000，23(3):68-70.