高阶混沌振子的微弱信号频率检测新方法

徐艳春，杨春玲

(1.哈尔滨工业大学 电气工程学院，哈尔滨150001，xyc7309@163.com;2.黑龙江大学 机电工程学院，哈尔滨150080)

由于混沌系统对初值和扰动的敏感性，使其在很多领域得到广泛应用.混沌理论在信号检测方面的应用近几年也引起人们的广泛关注.目前，该理论已被成功地应用于微弱信号检测当中，并取得较大进展.研究表明，大多数检测方法是在信号频率已知的条件下去测量弱信号的幅值，并没有提及如何检测信号的频率.而有些研究采用混沌理论测量频率的方法是在Duffing 方程的基础上，采用78 个振子阵列进行频率检测，该算法不仅复杂且只有当振子频率增加到某一成分信号频率附近时，才可以从时间图像上清晰观测到阵发混沌现象，检测方法繁琐［1-3］.

本文将Rossler 混沌系统和比例微分控制方法相结合，提出基于Rossler 混沌控制的强噪声背景下正弦周期信号频率检测的新方法.该方法最大特点是利用Rossler 混沌振子和比例微分控制进行信号频率检测.首先，通过比例微分控制，将正处在混沌状态的系统控制到周期轨道，从而使系统呈现出周期运动.当然，前面所说的混沌状态的系统是因为含有噪声的待检测信号的输入才处于混沌态，这种混沌态蕴含着待检信号的信息.此时，若直接用谱分析方法测频率，并不能测出待检周期信号的频率，本文用比例微分控制方法将其控制到稳定周期态后，再用谱分析方法则可测出未知信号的频率.

1 Rossler 混沌系统的特性研究

1963 年美国气象学家Lorenz 在数值试验中偶然发现了第一个混沌吸引子，不久，德国物理化学家O.E.Rossler 于1976 年指出，还可以用两种不同的方法从Lorenz 吸引子中抽出更简单、非对称的吸引子结构.一是研究Lorenz 方程组中的r 值远远大于28 时的情况;二是重新构造Lorenz 吸引子的折叠过程.这两种方法都可以得到同一拓扑结构，方程中虽只含一个非线性项xz，但却能产生混沌运动的非线性动力系统，这就是Rossler 系统［4-6］.

Rossler 系统是一个简单的而又内禀复杂的非线性系统，系统的方程为

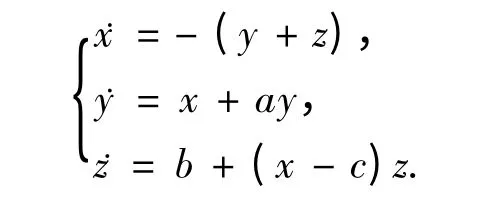
Rossler 系统比Lorenz 系统简单，而且拓扑不等价，即不存在任何的微分同胚变换把Rossler 系统转化成另一个系统.

Rossler 系统是一个三阶自治系统，含有一个非线性项xz，正是这个非线性项使系统产生分叉、混沌等复杂的动力学行为.其中方程在a =b=0.2，c 为不同值的时候，Rossler 吸引子的形状如图1 所示.事实上，Rossler 系统的任何一个方程对周期信号都很敏感，输入微弱的周期信号会对系统行为产生很大的变化［7］.

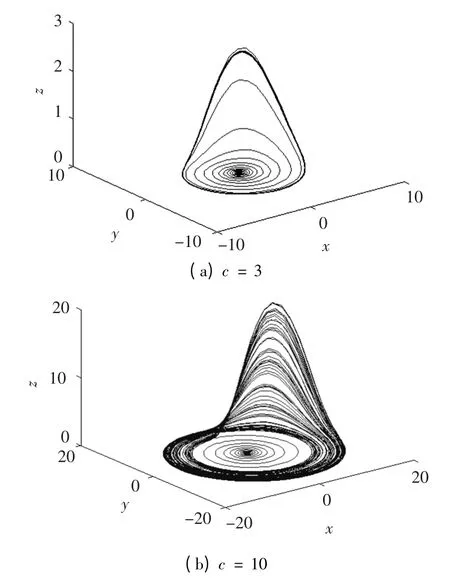
图1 c 为不同值时Rossler 吸引子相图

对Rossler 系统进行稳定性分析如下.取a=0.3，b=0.2，c=5 进行研究.

令

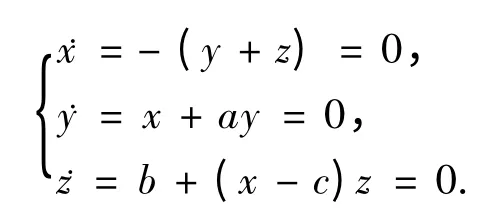
这样得到系统的两个平衡点为:s1=(0，0，0);s2=(-ab+c，(ab-c)/a，-(ab-c)/a).即s1=(0，0，0)，s2=(4.94，-16.47，16.47).

下面讨论这两个平衡点的稳定性.

对于平衡点s1=(0，0，0)，其雅可比矩阵J为

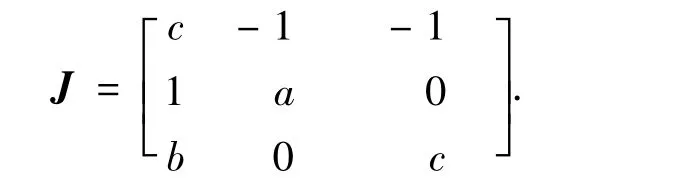
它的特征方程为

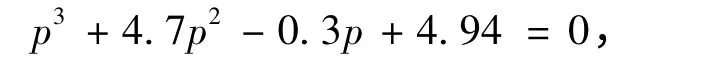
所以其特征值为

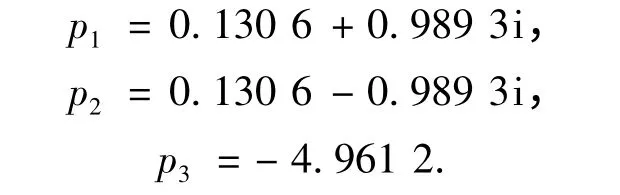
因特征值p1，p2有正的实部，而p3有负的实部，故s1=(0，0，0)是不稳定焦点.

对于平衡点s2=(4.94，-16.47，16.47)，其雅可比矩阵J 为

其特征值分别为

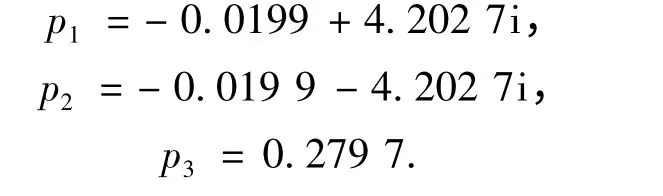
因其特征值p1，p2有负的实部，而p3有正的实部，所以s2为不稳定的鞍点［8-10］.

2 比例微分控制策略

考虑如下的n 维非线性动力学系统:

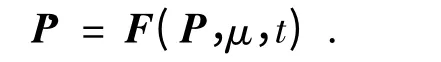
其中:P ∈Rn，F=［f1，f2，f3，…，fn］是n 维光滑的向量场;μ 为系统的参数，当μ 取一定范围的值时，系统处于混沌运动.

现对上式所表示的系统的状态变量Pm取比例微分控制得

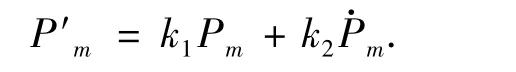
其中:k1，k2是本控制方法中的2 个可调参数，调整k1，k2的值可以实现不同的控制目标.将按如下方法进行反馈:

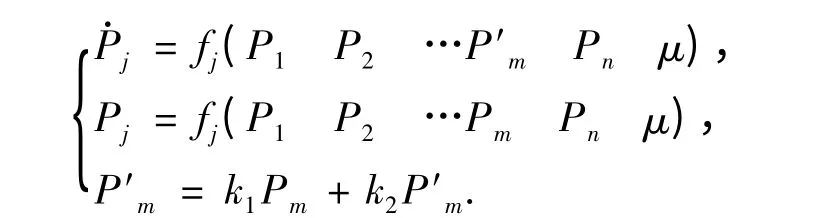
其中，j=1，2，…，n.

由上式所示的反馈方式可知:F()中的子系统fm()不受反馈控制作用而自由演化.若系统fm()中无状态变量xm，也不受控制作用而自由演化，则本控制方法只需对系统的一部分子系统进行控制，这就大大减小了控制的代价和在实际工程系统中实现控制的难度，克服了目前大多数状态变量反馈法需要多个进行全局反馈的缺陷.同时，比例微分控制法不影响原系统的特性，其结构相对简单，控制结果非常丰富，只要控制参数取很小的数值，就能十分有效地实现对非线性动力学系统的混沌控制，且控制速度快，这也正是本文采用此控制方法的原因.

3 基于Rossler 混沌控制的未知信号频率检测方法

本文采用Rossler 混沌系统进行信号频率检测，利用该系统对输入的周期信号敏感，输入微弱的周期信号会对系统行为产生很大变化的特点，将待检测的被噪声淹没的信号加入到Rossler 系统的任一个方程中，从而构成有待检信号的混沌系统.若此时对该混沌系统进行频谱分析，则频谱图曲线上的角频率将是ω，3ω，5ω，…，或者是2ω，4ω，6ω，…，此时表现为幅值高低不同且频率各异的若干信号，无法知道哪个频率是所求的.然而，当系统被控制到周期状态时，不管是奇阶超谐解还是偶阶超谐解，基频(待检频率)的幅值最大、最清晰.因此利用前面的比例微分控制理论将混沌系统控制到周期运动状态，最后通过频谱图非常容易检测出频率值.

具体控制算法及步骤如下:

1)调整Rossler 混沌系统参数，使其处于混沌的临界状态;

2)加入含有噪声的待检测的微弱信号，从而系统进入混沌态;

3)采用上述比例微分控制策略，调整控制参数，使其从混沌态进入周期态;

4)控制后的系统输出中含有待检信号的信息，对其进行频谱分析，从而检测出待检信号的频率.

文中选择y 为受控变量，为了讨论方便，不失一般性，令k1=1，按上述控制方法得受控后的方程为

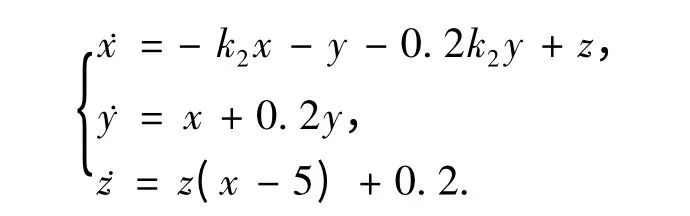
对不动点s2=(4.94，-16.47，16.47)进行研究，将系统进行线性化，得其雅可比矩阵J 为

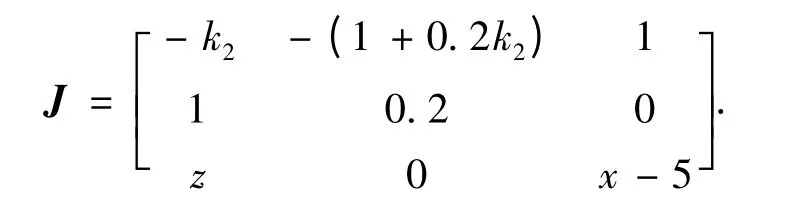
把J 代入其特征多项式为

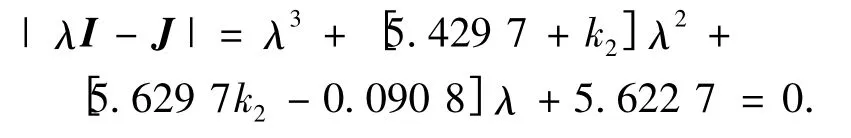
由Routh-Hurwitz 判据得，当0.016 3 ＜k2＜287 653.466 7 时，系统的不动点是稳定的.

从理论上来说，将待检测的微弱信号加入到3 个方程中的任一个方程均可改变系统的动力学行为，文中将待检信号加入到Rossler 混沌系统的第二个方程中进行分析.

4 数值仿真

图2 为k2=10，混沌系统未含有待检信号时Matlab 仿真结果，从图中可看出这种控制方法是有效的，系统通过这种控制能很好地控制到平衡点.

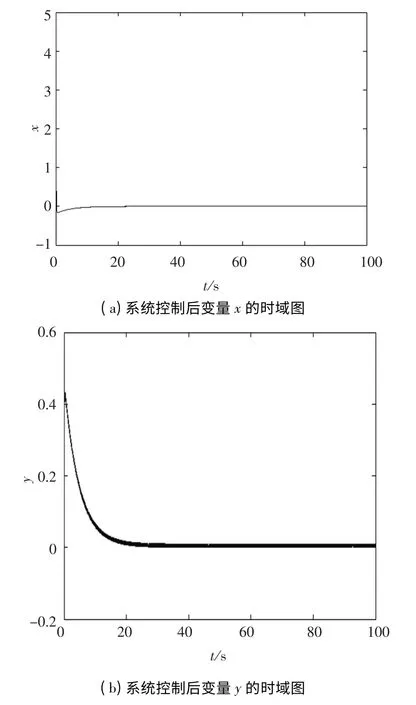
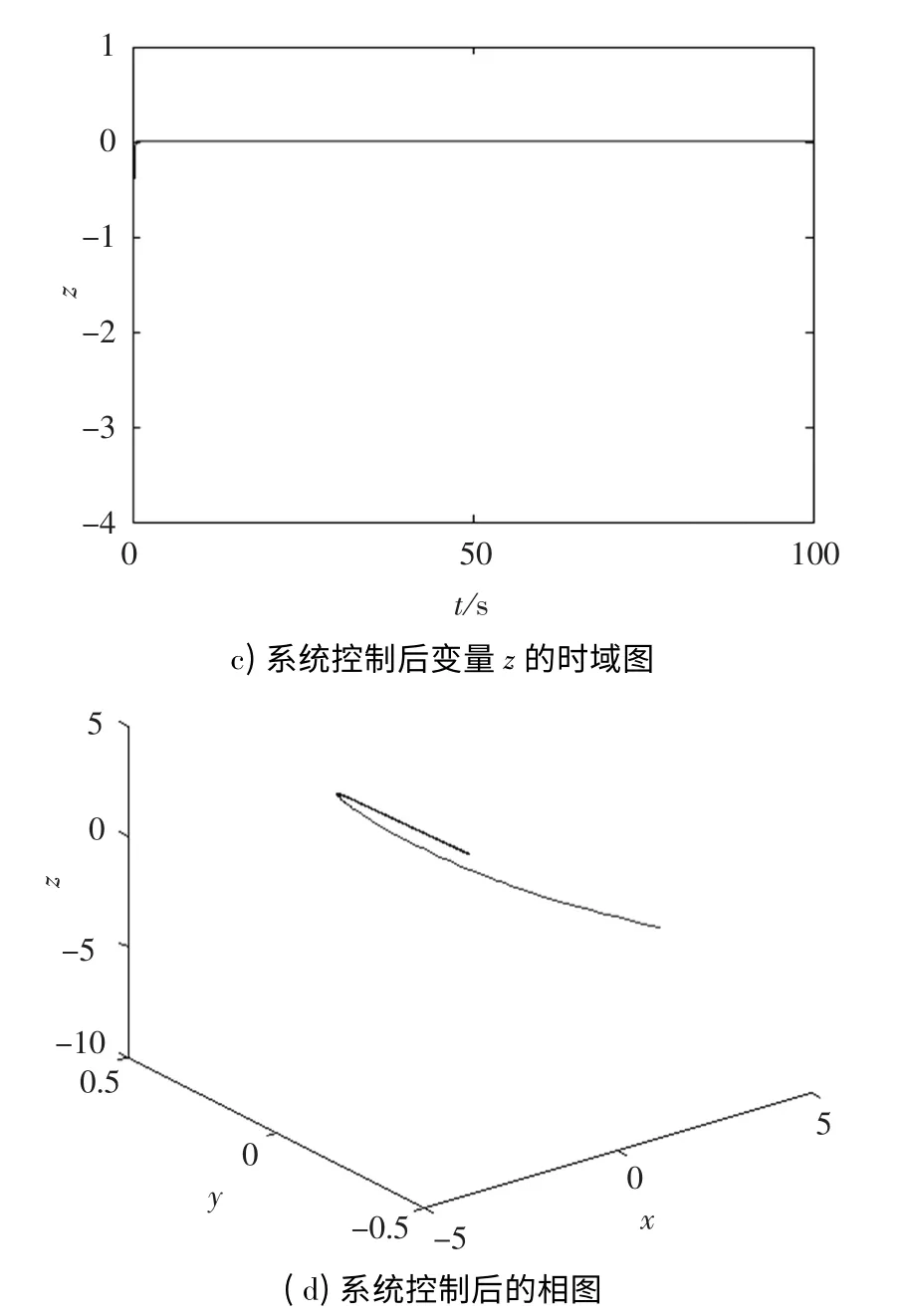
图2 系统控制后的时域图和相图

设待检信号为

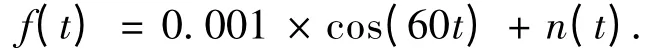
其中，待检信号的角频率为60 rad/s，幅值为0.001 V，n(t)是均值为零、方差为0.1 的白噪声.输入信号加入到Rossler 混沌系统第二个方程后系统的相轨迹及谱分析如图3 所示.

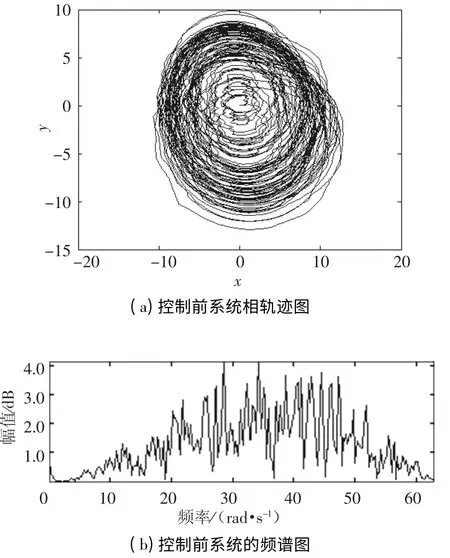
图3 输入信号后Rossler 系统的相图及谱分析图

由图3 根本辨认不出输入信号中的待检周期信号.图4 采用比例微分控制方法将Rossler 混沌系统控制到周期态后进行待检信号的频率检测.

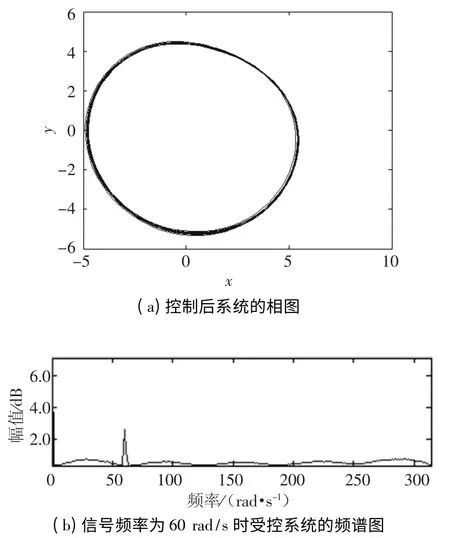
图4 控制后系统的相图和谱分析图

由图4 可直观准确的看出，待检的周期信号频率为60 rad/s.

当待检信号频率为200 rad/s 时，系统的频谱图如图5 所示.

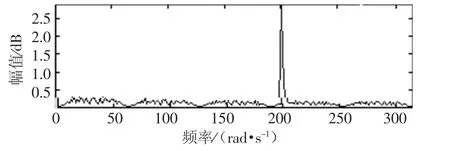
图5 受控系统的频谱图

经过大量的仿真实验，将在相同输入信噪比情况下，对本文提出方法和Duffing 阵列方法频率检测的结果进行比较，从表1 给出的实验结果可以看出，本文提出的微弱信号频率检测方法相对Duffing 方程振子阵列检测方法来说具有更大的优势，其在检测精度上较Duffing 系统检测方法有较大的提高.

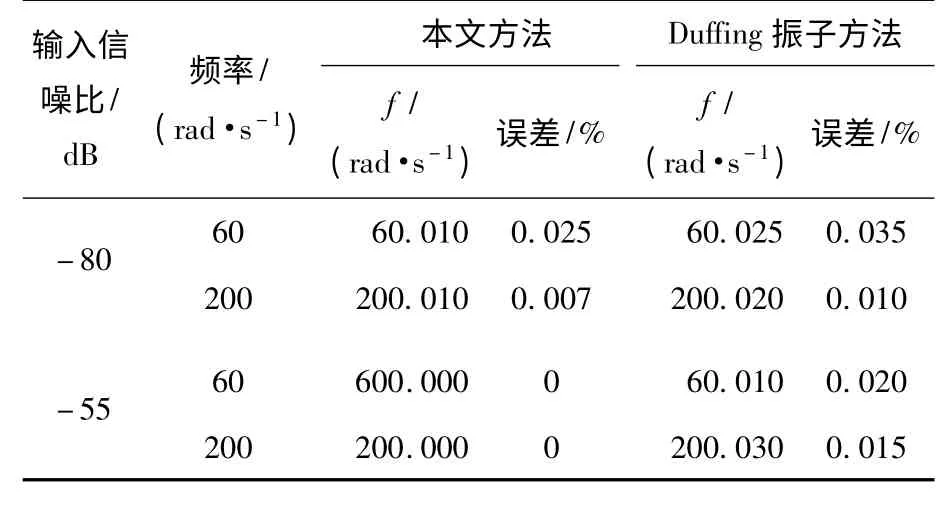
表1 2 种方法对微弱信号频率检测结果比较

5 讨 论

对于Duffing 方程在以往混沌检测信号方法中，Acos ωt 作为策动力，然后外加待检信号，此时，要求待检信号的频率与周期策动力的频率相同，最后，根据相轨迹的变化来测出待检信号的幅值.在此过程中并没有测量频率;也有一些文献专门利用Duffing 方程振子阵列进行信号的频率检测，但所需振子阵列较多，采用78 个固有频率以公比1.03 成等比数列的振子构成阵列，w1=1，w2=1.03，…，wk=1.03wk-1，…，w78=9.738.若频率在1 ～10 Hz 的被检信号输入到阵列中，就会在两个相邻的振子上发生稳定的间歇混沌运动，由此检测出信号的频率.因而只有当振子频率增加到某一成分信号频率附近时，才可以从时间图像上清晰地观测到阵发混沌现象.

应用本文提出的微弱信号频率检测方法，对不同信噪比下的正弦周期信号进行了大量的检测仿真实验.从仿真结果可以得到，本文提出的微弱信号检测方法可以实现从强噪声背景中检测出待检信号的频率，不受频差及策动力的限制，待检信号的频率通过频谱图可以直观准确的被测出.

6 结 论

将比例微分控制方法引入到Rossler 混沌系统中，构成一个带有控制项的混合系统.然后，将混有噪声的待检周期信号通过这个混合系统，调节控制项使混沌态转变成周期态.从信号处理领域来讲，相当于将噪声滤掉，显露出待检周期信号，然后，再将混合系统输出的信号通过频谱分析，在频谱图中显示幅值最大的所对应的频率就是待检信号的频率.此方法克服了Duffing 测量系统必须使用多个振子阵列的局限.实验仿真表明:本文提出的方法能够检测出深埋于强噪声中的微弱正弦信号的频率，且其检测精度较Duffing 系统检测方法更高，证明了该方法的有效性，其在理论上是可行的.

［1］聂春燕，石要武.互相关与混沌共同检测弱信号方法研究［J］.仪器仪表学报，2001，22(1):32-35.

［2］聂春燕，石要武.混沌系统检测nv 级信号方法的研究［J］.电工技术学报，2002，17(5):87-90.

［3］WANG Guan-yu.Application of chaotic oscillators to weak signal detection［C］//IEEE Transaction on Industrial Electronics.Piscataway:［s.n.］，1999:440-444.

［4］YI Wen-suo，SHI Yao-wu，NIE Chun-yan.The chaotic oscillator estimate method for sin wave parameter in nongaussian color noise environment［C］//The Sixth International Conference on Electronic Measurement and Instrument.Harbin:［s.n.］，2004:151-155.

［5］NIE Chunyan，SHI Yaowu，WANG Zhuwen，GUO Bin.A detection method of signal frequency based on optimization theory［C］//Sixth International Symposium on Instrumentation and Control Technology:Signal Analysis，Measurement Theory，Photo-Electronic Technology and Artificial Intelligence.Beijing:［s.n.］，2006:323-327.

［6］汪芙平，郭静波，王赞基.强混沌干扰中的谐波信号提取［J］.物理学报，2001，6(50):1019-1023.

［7］MACKAY R S，TRESSER C.Transition to topological chaos for circle maps［J］.Physics D，1986，19:206-237.

［8］王伟，张秋富.Rossler 系统的比例微分控制［J］.重庆工学院学报:自然科学版，2008，4(22):136-138.

［9］CHOE C U，HOHNE K，BENNER H，et al.Chaos suppression in the parametrically driven Lorenz system［J］.Physical Review，2005，72(5):362-366.

［10］SONG C Y，LEI Y H，DING S Q.Application of chaos to weak signal detection［J］.Editorial Board of Journal of Harbin Engineering，2004，25:21-23.