基于蒙特卡罗模拟的边坡可靠度评价＊

李 隐,邓 建,彭 泽

(中南大学资源与安全工程学院, 湖南长沙 410083)

基于蒙特卡罗模拟的边坡可靠度评价＊

李 隐,邓 建,彭 泽

(中南大学资源与安全工程学院, 湖南长沙 410083)

土坡稳定分析是十分重要的问题。定值分析法是目前工程设计中常用的分析方法,然而由于没有考虑实际存在的不确定性,得到的结果往往不能真实反映边坡实际状态。边坡可靠度分析法是在传统的确定性分析基础上发展起来的一种更符合客观实际的边坡稳定评价方法,它建立在概率统计基础上,以随机变量和随机过程为研究对象,因此更符合客观实际。边坡可靠度分析中的蒙特卡罗模拟,其收敛性与边坡极限状态方程的非线性,变量分布的非正态性等因素无关,适应性强,是一种有效的大型复杂边坡工程的可靠度分析与评价方法。采用条分法分析土坡稳定性,并通过蒙特卡罗法,对边坡可靠度进行分析,结合工程实例,讨论了土性参数的均值和变异系数对可靠指标的影响。

不确定性;可靠度分析;蒙特卡罗法;可靠指标

边坡稳定性问题一直是岩土工程学科中一项重要的研究内容[1]。传统的边坡稳定求解方法是将影响边坡稳定的诸因素看作确定性量,用安全系数作为衡量边坡稳定状态的指标。这种定值设计法是经过长期工程实践证明的一种有效设计方法。然而,边坡工程地质条件及岩体性质参数具有不确定性,得出的安全系数并不能客观地反映边坡的真实安全程度。边坡工程可靠度分析是把边坡岩体性质、荷载、地下水、破坏模式,计算模型等作为不确定量,借鉴结构工程可靠性理论方法,结合边坡工程的具体情况,用可靠指标或破坏概率来评价边坡安全度[2]。近年来,边坡随机可靠度分析理论与实践得到广泛重视和迅速发展[1～6]。目前常用的可靠度分析方法主要有一次二阶矩法[4],改进的一次二阶矩法(即验算点法),JC法,随机有限元法[5],概率矩点估计法[6],蒙特卡罗随机模拟方法[7]等。祝玉学[2]等对边坡随机分析进行了系统研究,为边坡可靠性分析作了大量基础工作。吴世伟[8]对土坝稳定可靠度作了大量研究。姚耀武等[9]对土坡中的楔体破坏进行了稳定性分析。与传统的确定性理论相比较,可靠性分析能更好的反映边坡工程的实际状态,正确合理的解释许多用确定性理论无法解释的工程问题,但是该方法还处于研究和探索阶段,还有待进一步发展完善。

1 模拟的精度和效率

蒙特卡罗法是一种以概率和统计理论、方法为基础的计算方法,它将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解,故又被称为统计模拟法或统计试验法[10]。

由于随机抽样试验是概率为 Pf的伯努利试验,N次抽样中的失效数 Nf服从二项分布。蒙特卡罗模拟的结构失效频率的均值、方差为:

而抽样方差可表为:

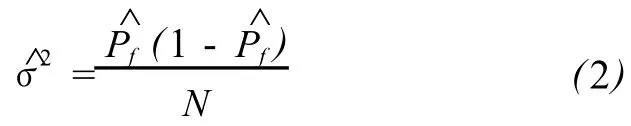
用正态分布来逼近二项分布,取 95%的置信度来估计失效概率,则

失效概率的相对误差为:

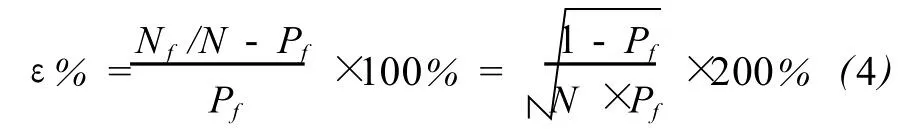
考虑到 Pf是一小量,故有:

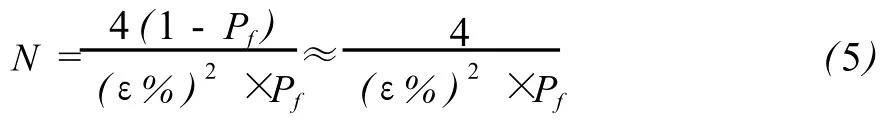
显然,抽样数N与结构失效概率 Pf成反比。若ε%=20%,Pf=10-4,则 N=106才能保证模拟的精度。

2 边坡稳定评价标准与分析程序

依据失效概率的大小可以将边坡分为 5种类型[2]:失效概率小于 5%的边坡评价为稳定;失效概率在 5%～30%之间的边坡评价为基本稳定;失效概率在 30%～50%之间的边坡评价为稳定性一般;失效概率在 50%～80%之间的边坡评价为稳定性差;失效概率大于 80%的边坡评价为稳定性极差。

GB50199-94规定水工结构应达到的可靠指标见表1[11]。其中第一类破坏是指非突发性破坏,破坏前能见到明显的征兆,破坏过程缓慢;第二类破坏是指突发性破坏,破坏前无明显的征兆,但结构一旦发生事故,难以补救和修复。

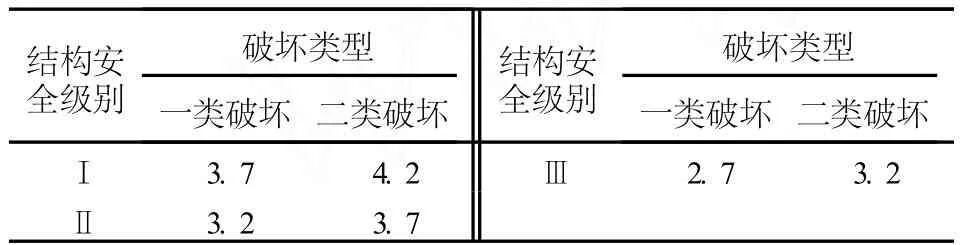
表1 目标可靠指标βr

根据蒙特卡罗的思路,编制边坡稳定计算程序,基本步骤如下:输入各随机变量均值,方差及分布类型;采用协方差矩阵将相关变量转换为不相关变量;随机产生一组均匀数,并生成服从变量分布规律的一组参数;通过逆变换生成初始变量互不相关的一组参数;分别带入 BISHOP功能函数,重复计算 N次,统计失效次数,从而计算出失效概率;检查失效概率的稳定性,必要时增加抽样次数 N,重复计算;计算安全系数的均值及方差,同时检验其分布规律,计算边坡的可靠指标[12]。

在生成随机数时可以利用MATLAB编写 c,φ正态分布函数,这种方法比较简单、省时,由于计算机运行能力的提高,模拟次数通常可取到十万至数百万次,完全能满足计算精度的要求。

3 工程实例计算

3.1 模型建立

以大宝山边坡为计算实例。该边坡为土质边坡。本边坡实例没有考虑土体抗剪强度指标 c,φ值相关性,仅考虑计算参数的变异性及分布规律对边坡可靠指标和失效概率的影响。边坡模型分为 3个土层(见图1),土层 3中含有地下水位线,因此可以将含有水位线的土层分为两个土层(见表2)。

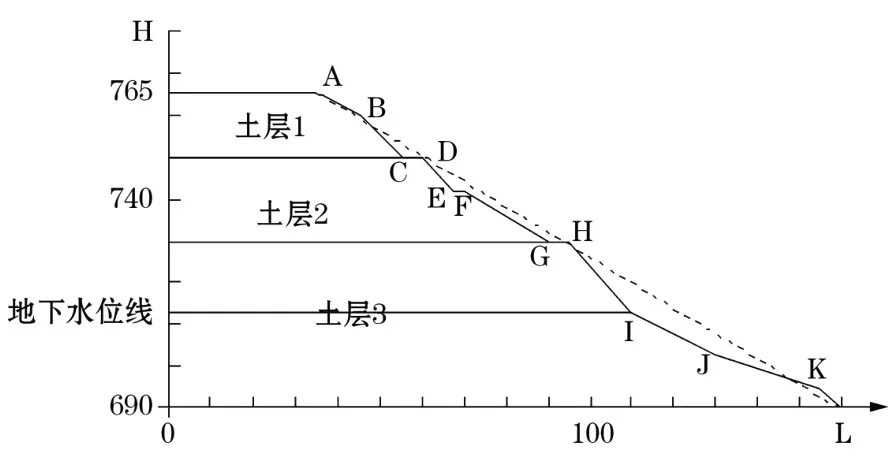
图1 边坡剖面

表2 土层参数

3.2 可靠度分析与评价

在边坡可靠度分析中,土的凝聚力 c和内摩擦角φ的影响比γ大得多,故仅取 c和φ作为基本随机变量。根据现行的研究成果,c多成对数正态分布,φ多呈正态分布[13]。下面的计算和分析中取 c和φ均为正态分布。取变异系数δ=0.3,取土层 1和土层 2的 c和φ为随机变量,分别为 c1,c2,φ1,φ2。

毕肖普法边坡稳定可靠性分析的功能函数为:

利用MATLAB对 4个随机变量各自生成 N个随机数,得到 N组随机数。分别带入 BISHOP法的REAME程序,计算出相应的 Fs值,代入式(6),得出 Z值。统计出 Z≤0的失效次数 Nf,当总次数 N足够多时,计算结束。最后由 Pf≈Nf/N计算边坡失效概率。模拟结果列于表3。当 N足够大时,边坡失效概率始终保持在 Pf≈0.7%。由公式(5)可知,当 Pf≈0.7%时,N=14300才能保证模拟的精度。此时,失效概率已趋于稳定。

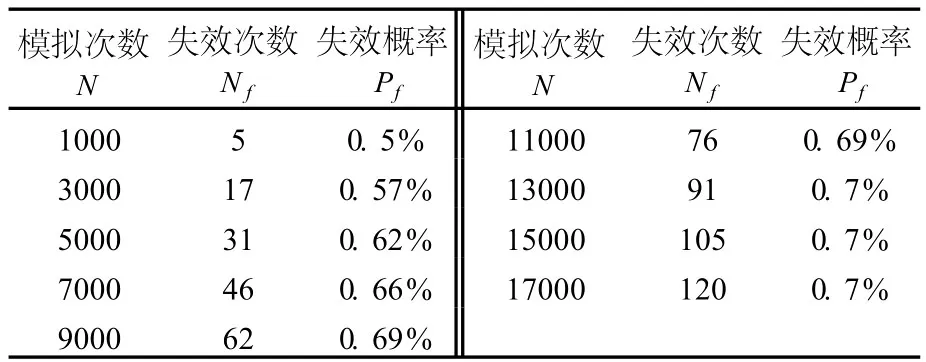
表3 统计失效概率

功能函数中包含有 4个相互独立的正态随机变量 Z=(c1,c2,φ1,φ2),边坡安全系数可以表达为以下一个广义的函数:

式中,c1,c2,φ1,φ2为影响边坡稳定的基本变量。

可靠指标计算公式为:

式中,μF,σF分别为 Fs的均值与标准差。

依据失效概率评价边坡稳定,Pf≈0.7%,远远小于 5%,初步判断边坡稳定。依据可靠指标,β=4.8,分别大于一类破坏的第一安全级别和二类破坏的第一安全级别,可以判定边坡稳定。

3.3 参数变异性对β的影响

变异系数δ=σ/μ是反映随机变量的不确定性的一个重要指标。为进一步研究土性指标的随机性对边坡稳定性的影响,选取影响较大的两个强度指标 c和φ的变异系数[5]进行讨论。

分析 c的变异性对β的影响时,假定δφ=0,取δc的变化范围为 0.1～0.5。从图2可以看出,c的变异性对β的影响显著。δc=0.1时,β=9.2。而当δc增大到 0.5时,β为 2.7。

图2 β和 c变异系数关系曲线

分析φ的变异性对β的影响时,假定δc=0,取δφ的变化范围为 0.1～0.3。当 δφ=0.1时,β=12.3,而当δφ=0.3时,β仅为 4.8,说明 δφ对 β影响也非常显著(见图3)。可靠性指标β对土性指标的变异性相当敏感,当 c和φ的变异系数为不同的值时,β相差很大,规律是随着变异系数的增大,可靠指标变小。

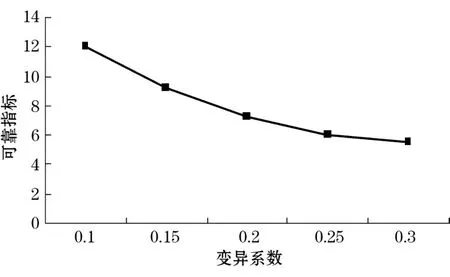
图3 β和φ的变异系数关系曲线

4 结 论

(1)本文用土坡稳定分析方法中最常用的条分法——简化 Bishop法建立了可靠度分析的极限状态方程,并与蒙特卡罗法可靠度分析程序结合起来,讨论了土性参数的均值和变异系数对可靠指标的影响。分析表明,蒙特卡罗法评价边坡可靠度,受条件限制的影响较小,其收敛性与边坡极限状态方程的非线性,变量分布的非正态性等因素无关,适应性强,是一种有效的大型复杂边坡工程的可靠度分析与评价方法。

(2)本文对土坡可靠度分析中的一些规律性的问题进行了深入研究,得到一些初步认识。这对今后在土坡可靠度分析中很有参考意义,对制定按可靠度理论的土坡设计规范也具有参考价值。

[1] 陈祖煜.土质边坡稳定分析(原理、方法、程序)[M].北京:中国水利水电出版社,2003.

[2] 祝玉学.边坡可靠性分析[M].北京:冶金工业出版社,1993.

[3] Li K S,Lumb P.Probabilistic design of slopes[J].Canadian Geotechnical,1987,24(4):520～535.

[4] Christian J T,Ladd C C,Baecher G B.Reliability applied to slope stability analysis[J].Journal of geotechnical engineering Division,1994,120(12):2180～2207.

[5] Deng Jian,Gu DS.A reliability based approach for evaluating slope stability under seismic loadings[A].9th International conference on structural reliability and safety[C].Rome,Italy:June 19～22,2005:175～181.

[6] 苏永华,何满潮.利用矩点估计法简化响应面可靠度指标的计算[J].工程力学,2007,24(7):11～15.

[7] 徐钟济.蒙特卡罗方法 [M].上海:上海科学技术出版社,1996.

[8] 郑 铎,吴世伟.土坝稳定可靠度分析方法初探[A].全国第三届工程结构可靠性学术会议论文集[C].南京:[s.n.],1992,612～617.

[9] 姚耀武,陈东伟.土坡稳定可靠度分析[J].岩土工程学报,1994,16(2):80～87.

[10] Deng Jian,Gu Desheng,Li Xibing.Structural reliability analysis for implicit performance function using artificial neural network[J].Structural Safety,2005,25(1):25～48.

[11] 赵寿刚,兰 雁,沈细中,等.蒙特卡罗法在土质边坡可靠性分析中的应用[J].人民黄河,2006,28(5):65～66.

[12] 钱家欢,殷宗泽.土工原理与计算(第二版)[M].北京:中国水利水电出版社,1996.

[13] 韩玉芳,刘德辅,董 胜.边坡整体稳定的可靠性分析方法[J].海岸工程,2001,20(4):7～13.

高等学校博士学科点专项科研基金(200805330029).

2009-09-09)

李 隐(1984-),男,硕士研究生,安徽淮北人,主要从事岩土工程边坡稳定性分析,Email:jefflysci@yahoo.com.cn。