光学折射反射定律的两种不同的数学实现
石市委, 孙兆奇, 吕建国
(1.安徽大学物理与材料科学学院,安徽合肥 230039;2.合肥师范学院物理与电子工程系,安徽合肥 230601)
光学折射反射定律的两种不同的数学实现
石市委1, 孙兆奇1, 吕建国2
(1.安徽大学物理与材料科学学院,安徽合肥 230039;2.合肥师范学院物理与电子工程系,安徽合肥 230601)
文中分析了光学中折射反射公式的两种数学实现方法,矢量法和复数法。其中复数法应用方便简单,且在其他文献中未见有报道。
折射公式;反射公式;矢量法;复数法
1 前言
几何光学在当今的光学设计领域仍占有举足轻重的地位,它忽略衍射效应,认为光是沿直线传播的,故又称为线光学理论。这种忽略衍射效应的近似是有效且务实的,它可以使光学设计任务变得简洁而且直观,计算工作大为简化,并且结果在应用范围内足够精确。所以现在的光学设计理论主体仍然是几何光学。几何光学中光在介质分界面处的传输行为由反射定律和折射定律来描述,在具体的光学设计过程中需要处理大量的在界面处的光线折射和反射,传统的处理是将模型化的计算对象带入采用矢量法表示的反射定律和折射定律来计算出射光线,但这并非是唯一的一种处理方法。本文根据多年来编制光学计算程序的经验[1],给出计算光线折射和反射另一种方法,即复数法,该方法在应用到程序中时更方便直接。本文介绍这种方法的推导过程,希望可以对其他需要编制光学设计软件的人员及光学设计方向的教学人员有一定的帮助或参考。为便于比较,文中同时给出两种方法的推导过程和结论。
2 矢量形式的折射公式和反射公式
在不考虑光强变化的情况下,光学设计主要考虑的是光线在传输过程中的方向改变问题。对于由一种或多种均匀介质组成的光学系统,光线在传输的过程中光线方向的改变仅仅出现在介质的分界面处,而且严格依照折射定律和反射定律进行。计算过程中需要的是公式化的折射定律和反射定律,这两个定律的不同的数学表示对光学计算复杂度的影响是不同的,一个好的数学表达可以给光学计算带来很多方便。本文首先给出矢量形式的折射公式,然后给出复数形式的折射公式和反射公式。
(1)矢量形式的折射公式[2]
如图1所示,以分别表示入射光线和折射光线的单位矢量,n0和n1分别表示折射面两边的介质的折射率,矢量指向右为正方向,反之为负。为入射面入射点法线的单位矢量,顺着光线传播方向为正,反之为负。

图1 光线的折射——矢量法
折射定律可表示为:上式即为矢量形式的折射定律。


(2)矢量形式的反射公式
我们知道,在折射定律中若令n1=-n0,可得I′=-I的反射定律。现将此用于矢量形式的折射定律,由(3)式所表示的偏向常数为

3 复数形式的折射公式和反射公式
通常光线在遇到界面时,如果介质不是非线性或各向异性材料,光线的传播将被限制在入射光线和法线所在的平面(即所谓的入射面)内,即折射光线和反射光线亦处在入射面内。因此,在不考虑光强变化的情况下,由于仅仅是平面内的方向偏转问题,具有方向性的数学量肯定能承担界面处光线的偏转计算,如在复平面内变化的复数。下面给出用复数表示的折射公式和反射公式及其推导过程。
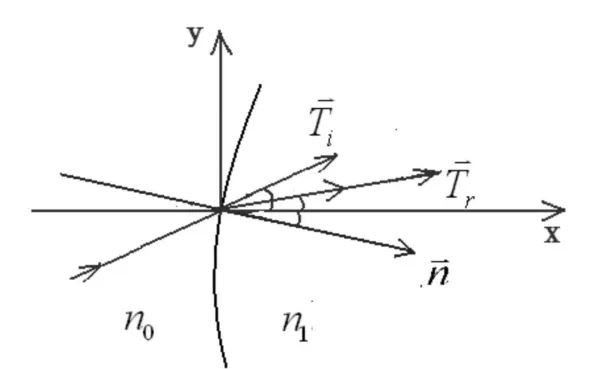
图2 光线的折射——复数法
(1)折射定律的复数形式
假设光线从折射率为n0的介质由界面入射到折射率为n1的介质,法线方向与参考坐标正方向的夹角分别为φn、φi和φt。
法线、入射光线和折射光线分别用模为1的复数表示:

根据(5)式所示的折射角和法线方向及入射角的关系,即可知道出射光线的方向

(9)式即为折射定律的复数形式。由实部与虚部的对应关系,可以进一步写出Tx1和Ty1

只要知道入射方向,法线方向,就可以唯一地确定折射光线的方向。(9)式表面上看起来比(5)式复杂,其实在实际编程时要容易实现的的多。使用(5)式进行编程需要进行多次迭代,而使用(9)式一步即可实现。
(2)反射定律的复数形式
入射光线折射光线法线分别表示为:


上式即为反射定律的复数形式。
由实部与虚部的对应关系,有

由上式可以看出,只要知道入射方向,法线方向,就可以唯一地确定反射光线的方向,而且它比(7)式更容易使用。
4 总结
本文给出复数形式的几何光学折射反射定律,使用起来方便直接。此结果不仅可作为光学课程教学时的一个拓展思维的教学实例来使用,而且可为光学设计人员提供又一种计算光线折射反射的方法。
[1] 易佑民,章于川,夏茹,等.聚合物梯度折射率微球透镜的研制[J].光子学报,2003,32(4):425-428.
[2] 周昆,李继陶,陈祯培编.应用光学[M].四川:四川大学出版社,2004:4-5.
The Expressions of Refraction Lawand Reflection Law in Optics
SHI Shi-wei1, SUN Zhao-qi1, LV Jian-guo2
(1.School of Physics and Material Science,A nhui University,Hefei230039,China;2.Department of Physics and Electronic Engineering,Hefei Normal University,Hefei230601,China)
Two kinds of expressions for refraction law and reflection law in optics are analyzed in this paper. The two expressions include vector expression and complex expression,the latter has not been found in the literature.
refraction law;reflection law;vector expression;complex expression
O441.1
A
1674-2273(2010)06-0017-03
2010-05-10
安徽大学青年科学研究基金重点项目(2009QN008A),安徽普通高等学校自然科学基金(KJ2010A284),光电信息获取与控制教育部重点实验室开放基金项目,安徽大学211工程三期教学质量工程项目[2304005(0006)]。
石市委(1978-),男,安徽界首人,安徽大学物理与材料科学学院教师,博士研究生。

