关于欧拉方程的进一步讨论

宋泽成

（唐山师范学院 数学与信息科学系，河北 唐山 063000）

在现行的教材中，都把形如

的方程称为欧拉方程，（其中 a1,a2,…, an是常数），并给出了其解法，如果定义形式仅局限于此，对于更深刻的理解欧拉方程，掌握欧拉方程的应用很不利，因此有必要将其从形式到解法进行推广，使其应用更广泛。

1 推广的欧拉方程及解法

定义1 形如

的方程（其中 a, b, a1, a2,… ,an均为常数）称为推广的欧拉方程。

a=1，b=0则方程(2)转化成方程(1)，因此方程(1)是方程(2)的特殊情况。

在方程（2）中令t=ax+b，则

代入(2)中得

即方程(2)也可转化方程(1)，进一步可按方程(1)的解法求解方程(2)。

例1 求方程

的通解。

解 作变换 z= 2 x+ 1，则有

代入原方程得

方程(4)的通解为 y = c1z+c2z2

原方程的通解为

定义2 形如

的方程称为非齐欧拉方程（其中 a1, a2,… ,an为常数）。当f( x) = 0时，方程(1)称为齐欧拉方程。

一般地，可先求齐欧拉方程的通解，然后利用常数变易法求非齐欧拉方程的通解，但比较麻烦，因此对于 f( x)的一些特殊情况可以直接作变换将其转化成常系数的线性方程，再利用欧拉待定指数函数法求解。

例2 求非齐欧拉方程

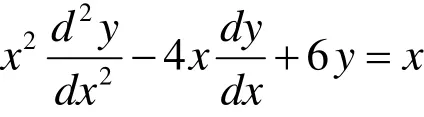
的通解。

解 作变换 x=eu，于是方程化为

利用待定系数法，求得(6)的通解为

将 u x=e代入上式，得到原方程的通解为

其中c1, c2为任意常数。

例3 求非齐欧拉方程

的通解。

解 作变换x=eu，于是方程化为

利用待定系数法，求得方程(7)的通解为

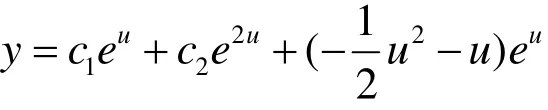
将x=eu代入上式，得到原方程的通解为

其中c1, c2为任意常数。

2 二阶齐欧拉方程一种特殊解法

定理 对于二阶齐欧拉方程

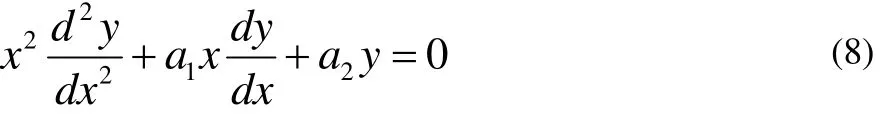
如果 a1=-a2，那么 y=x( x ≠ 0)是方程的一个特解，其通解为

代入方程(8)左边得，左=a1x+a2x；又 a1=-a2，所以左=0=右，即y=x是方程（8）的特解。

通解的证明见文献[1]。

例4 求欧拉方程

的通解。

解 因为a1=1，a2=-1，所以y=x是原方程的一个特解，那么方程的通解为

计算整理得