高精度干涉检验移相算法对振动误差的免疫能力
刘 艳,苏东奇,杨怀江,隋永新
(1.中国科学院长春光学精密机械与物理研究所,应用光学国家重点实验室,吉林长春 130033;2.中国科学院研究生院,北京 100049)
1 引 言
移相干涉术[1](Phase Shifting Interferometry,PSI)是 1974年由 Bruning等人提出的[2],他将该技术用于检验光学表面和透镜质量,开启了 PSI应用于光学测量领域的时代。
PSI作为一种精密测量手段,其测量精度通常受到干涉检验过程中各种误差源[3,4]的影响,包括移相器 (如 PZT)的标定误差、探测器的非线性误差和量化误差、光源的不稳定性、机械振动和空气扰动等等。因此,为了保证高精度的测量结果,提高测量精度的重复性,需要对这些误差源进行分析和校正。在这些误差源中,机械振动是影响最大的误差源,是限制 PSI技术精度的关键因素。干涉测量中,减小振动影响的预防措施一般有使用主动或者被动隔振装置;在设计过程中注意隔振的设计要求;对放置干涉仪的试验台做隔振设计等。另外,把干涉仪放置在安静的远离振源的环境中也是非常重要的。
移相过程中移相值的不稳定性通常来源于小幅度的振动,可以使用类似处理移相误差的分析方法进行分析处理。本文主要针对移相过程中的小幅度机械振动进行了模拟分析,并把模拟结果与现有文献报道结果进行了对比。
2 移相干涉仪工作原理
移相干涉技术的原理是在干涉仪的参考光束和被检光束的相位差之间引入等间隔位移,当参考光程 (或相位)变化时,干涉条纹的位置也做相应的移动,移相方式有有步进式 (Stepping)和扫描式 (Scanning)两种。步进式是指压电传感器(Piezoelectric Transducer,PZT)推动参考镜步进一定的位相值并且系统达到稳定状态之后,CCD采集此时对应的干涉图;扫描式是指 PZT推动参考镜以一定的速率匀速前进,在前进的过程中,CCD以特定的时间间隔对干涉图进行采样。在积分时间为零的情况下,步进式可以看作扫描式的特殊情况[1]。
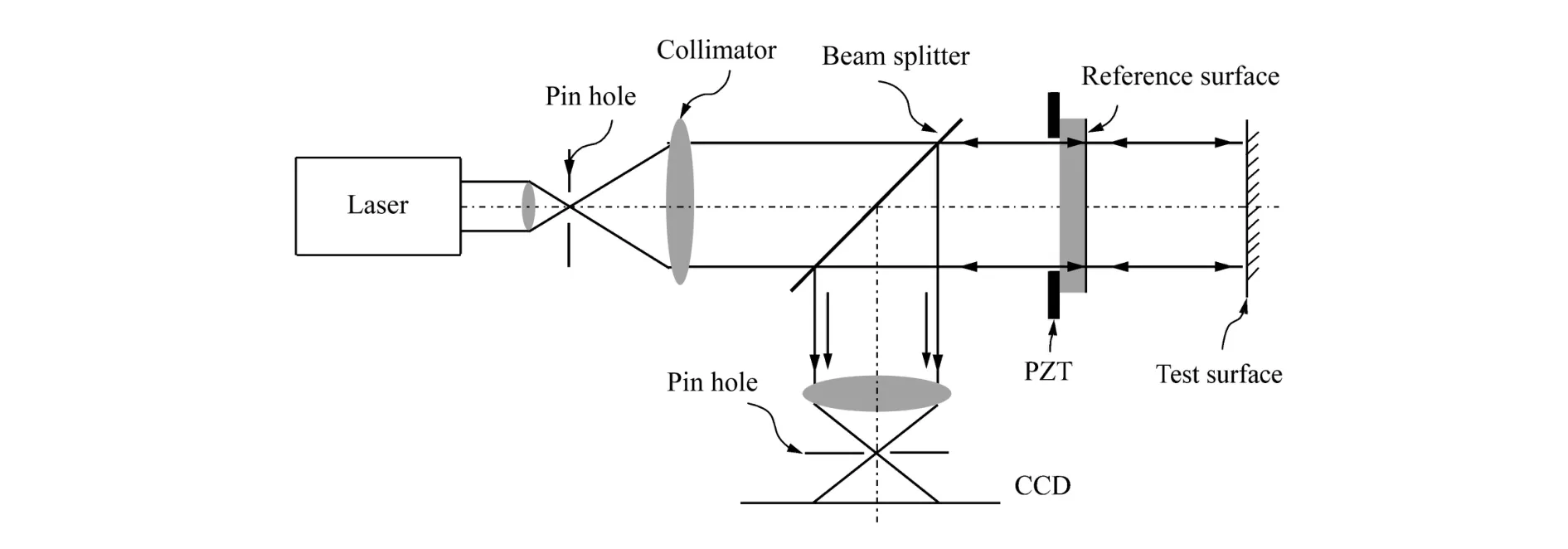
图1 移相 Fizeau干涉仪工作原理Fig.1 Schematic diagram of phase shifting Fizeau interferometer
图1所示为移相 Fizeau干涉仪检测平板的工作原理示意图。由光源 (一般采用波长为 632.8 nm的稳频 He-Ne激光器作为光源)输出的单频激光被会聚透镜会聚在小孔处 (起到空间滤波的作用),经小孔滤波,到达准直镜,经准直之后,会聚光变为平行光。从准直镜出射的平行光,经过分束镜分光,分光后的光束,经过参考镜的透射面,到达参考镜的参考面,参考面上镀有金属膜,使一部分光到达带有楔度的参考镜的参考面后被反射回来作为参考光,另一部分光穿过参考面后到达样品待测表面再反射回来作为待测光。参考光和待测光再通过分束镜反射到达成像透镜,发生干涉,就会在 CCD处观察到等厚干涉条纹。计算机输出移相指令给 PZT驱动干涉仪的参考镜产生等间隔的位移从而引入相位调制,用 CCD对经调制的干涉图进行采样,将 CCD所接收的视频图像信号数字化后送入计算机,通过对数字移相干涉图的分析处理,即得到被测波面的相位分布[2]。这种数字波面移相干涉技术能得到很高的相位分辨率和空间分辨率。采用多幅干涉图采样,克服了单幅干涉图处理精度低的缺点,可以在一定程度上抑制噪声的影响。尤其对于随机噪声,对多幅干涉图进行平均运算,可以明显减少随机噪声造成的误差,具有噪声抑制能力强、实时、快捷、精度高等优点,从而获得更加真实的所测元件表面的相位分布信息。
3 建立振动误差模型[6]
以共光路 Fizeau干涉仪为例,一般通过 PZT精密控制干涉仪参考镜面的机械移动来产生等间隔位移,基于双光束干涉原理,有下面的表达式:
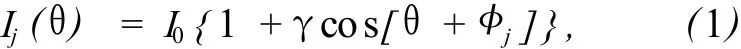
其中,j是移相的步数,Ij(θ)为移相过程中探测到的光强,I0为背景光强,γ为对比度,θ为参考光束和被检光束的相位差,即所需要求解的位相,φj为移相值。这些参数都是空间位置 (x,y)的函数。
假设干涉检测的过程中,存在如下所述的振动形式:
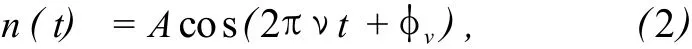
其中,A为振动的振幅,ν为振动频率,φv为振动的初始位相值。
那么振动引进误差的影响,等价于 PSI移相值 φj的不确定性,就是式 (1)中位相的位置加入振动n(t)。
对于七步算法:
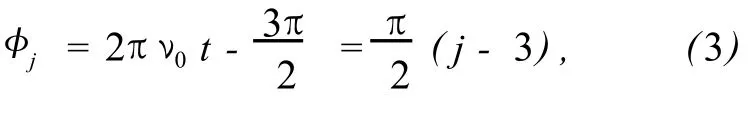
其中,ν0为采样频率,π/2为每步移相值,j=0,…,6。
可以得到:
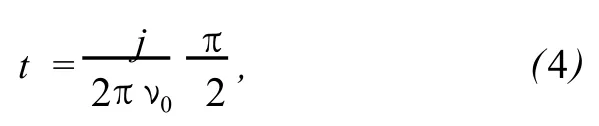
则:

令νn=ν/ν0为振动频率与采样频率的比值,对于一般算法设其移相值为α,则对于一般情况式(5)变为:
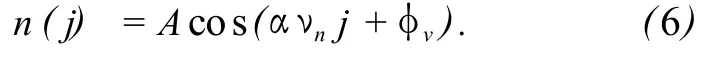
把振动式 (6)带入式 (1)后,得到:
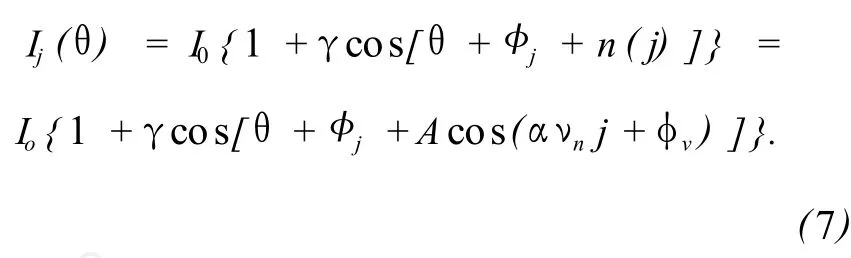
然后计算某一个振幅下不同的频率νn对均方根 (Root-mean-square)的影响,得出此算法情况下νn与均方根的关系。具体计算每个频率的影响是对一个周期内的φv求平均值,即去掉振动位相的影响。
为减小振动的影响,采用积分的办法,即对每次移相前后α/2范围的光强值进行积分:
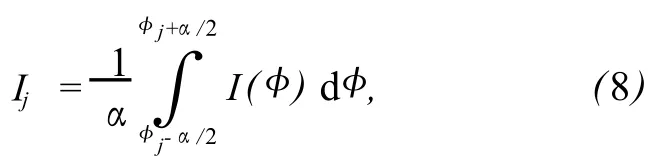
由 PSI求解相位的典型形式为:

本文中,Wyant84b三步算法T3(简称三步算法)[5],Hariharan87五步算法T5(简称五步算法),七步算法T7和十三步算法T13分别为:
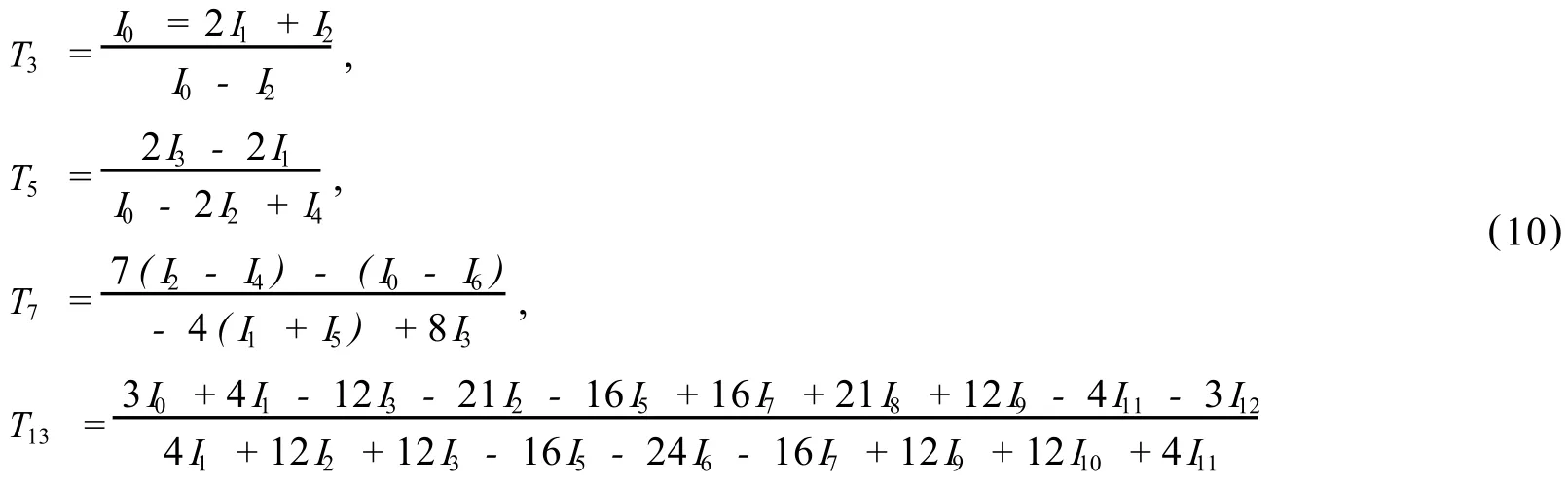
4 算法对振动的免疫能力对比
在本文误差模型的基础上,没有加入任何误差因素时算法的对比如图2所示,可以清晰地看到这 4种算法中,十三步算法的精度最高,具有最小的相位差。这里的相位差 (Phase Error)是指数值模拟中给定的相位值 (Real Phase)与由该算法计算得到的相位之差。下面分析移相算法对具有不同振幅和频率的振动的抑制能力。
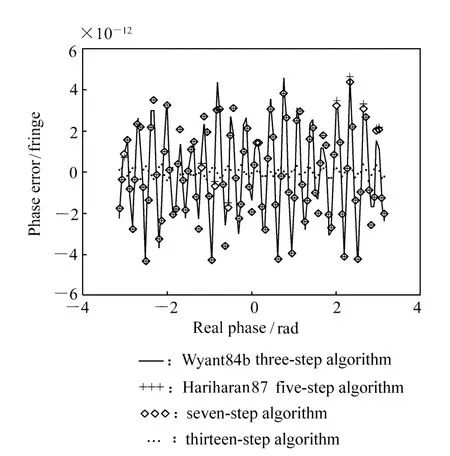
图2 没有引入误差因素时,4种算法对比Fig.2 Comparison of 4 algorithms in condition without errors
4.1 振动频率固定,算法抑制能力与振动振幅的关系
在振动频率等于采样频率,即νn=1时,得到了相位差与振动振幅的关系,如图3所示。可以看出,振幅越大,算法对振动的抑制能力降低。十三步算法在各振动振幅下都具有优于其它 3种算法的抑制能力,五步算法和七步算法的抑制能力略低于十三步算法,三步算法在振幅较小的情况下也具有较好的抑制能力。除此之外,移相算法的步数越多,计算时间越长,计算过程也越复杂,所以在振幅较小的检验环境中,同时对干涉检验精度没有特殊要求时,可以考虑使用移相步数少的算法以便减少数据处理时间。
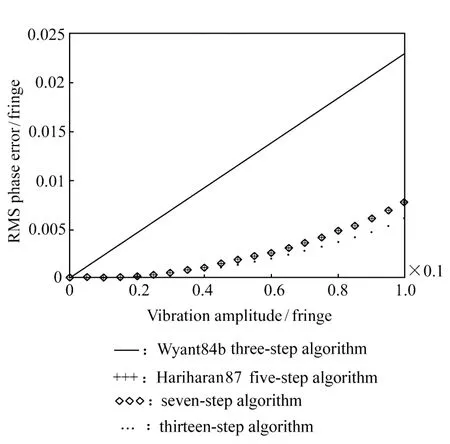
图3 振动频率等于采样频率,相位差 RMS值随振幅的变化Fig.3 RMS phase error varies with vibration amplitude when vibration frequency equals sampling frequency
图4给出了振动振幅分别为 0.02、0.1和 0.2 fringes时,相位差与真实相位值的关系,其中 fringes指干涉条纹,一个 fringe等于 2π弧度的相位。对图4分析可知,十三步算法在抑制振动方面具有明显的优势,与图3体现的各算法对振动的抑制能力强弱趋势相一致。

图4 存在振动时,4种算法对应的相位差与真实相位值的关系Fig.4 Relation between real phases and phase errors of 4 algorithms as vibration exists
4.2 振动振幅固定时,算法抑制能力与振动频率的关系
由图5和图6可以看出,在振幅一定的情况下,4种移相算法中十三步算法对振动的抑制能力最强,其余依次为七步算法、五步算法和三步算法。
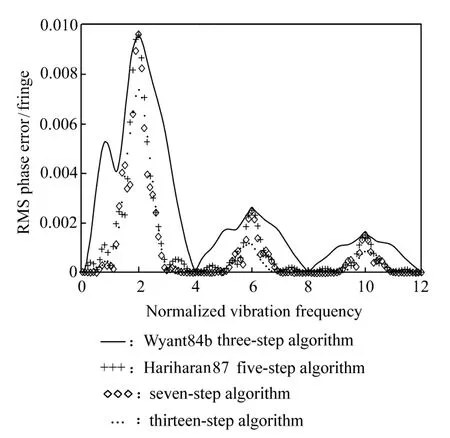
图5 振幅为 0.02 fringes,振动频率与相位差 RMS的关系Fig.5 RMS phase error varies with vibration frequency in vibration amplitude of 0.2 fringe
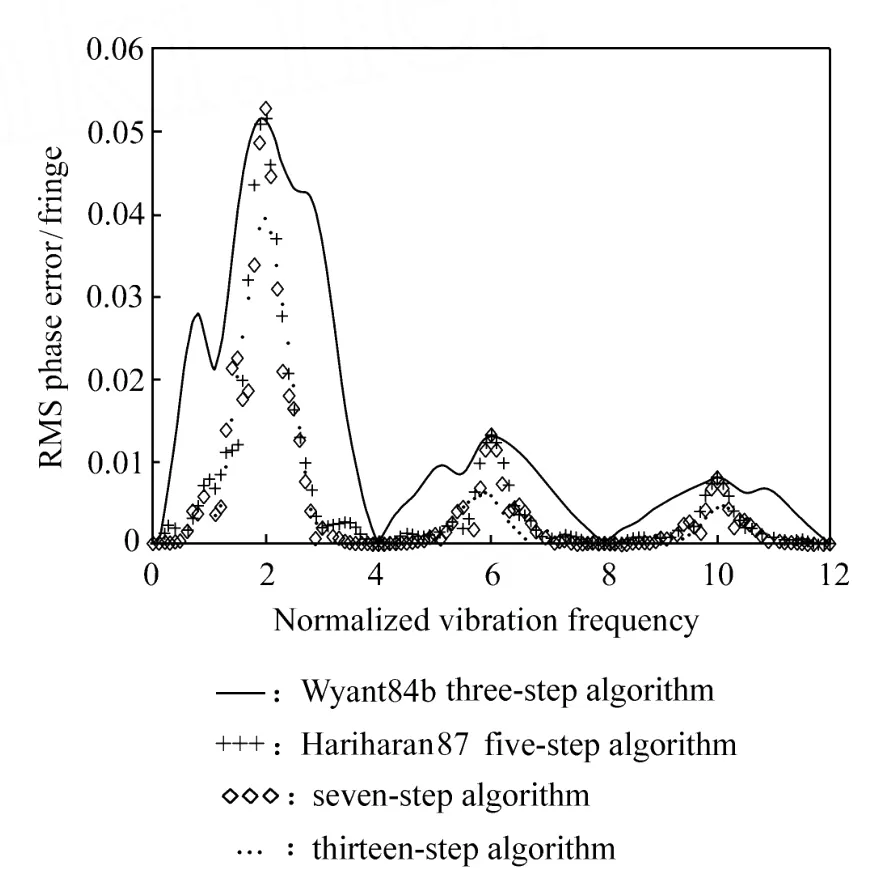
图6 振幅为 0.1 fringes,振动频率与相位差 RMS的关系Fig.6 RMS phase error varies with vibration frequency in vibration amplitude of 0.2 fringe
综上所述,对于具有一定振幅和振动频率的振动来说,本文提到的 4种算法中十三步算法具有最好的振动抑制能力。除振动之外,十三步算法在抑制移相误差等方面也很强大,所以十三步算法经常在实际的干涉信息处理软件中被采用。著名的美国干涉仪生产商 Zygo公司的计算机软件中多采用十三步算法。
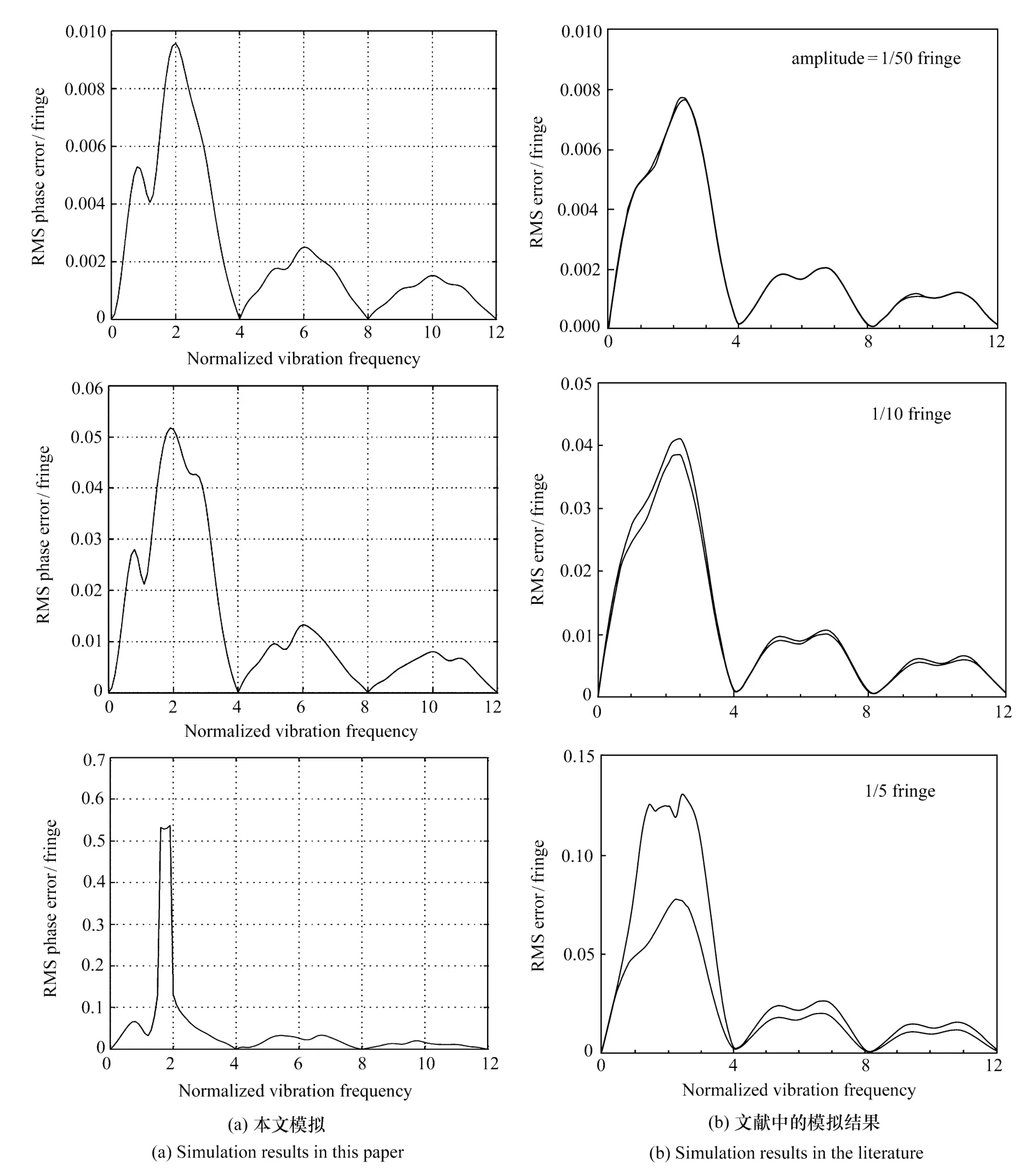
图7 三步算法模拟与文献对比:振幅确定时 RMS随频率的变化Fig.7 Comparison be tween the results of three-step algorithm and references:RMS varies with frequencywhen amplitude is determined
5 与文献报道对比
首先,以三步算法、五步算法、七步算法 (移相值π/2)为例,分别讨论振动幅度为 1/50,1/10,1/5 fringes时,振动频率与 RMS的关系。与参考文献 [6]的结果进行对比,如图7、图8、图9所示。为便于分析对比,对每一种算法分别进行了计算。

图8 五步算法模拟与文献对比:振幅确定,RMS随频率的变化Fig.8 Comparison between the results of five-step algorithm and literature:RMS varies with frequency when amplitude is determined
由图6可以看出,三步算法对振幅在 1/10 fringes以下的振动免疫力较好,对于更大振幅的振动其抑制能力大大减小,但是从下面的模拟图中仍然可以明确,不同的算法对振动的敏感程度与振动频率密切相关,在某些相同的归一化频率处这些算法对振动的抑制或最强 (如图中归一化频率 4,8,12)或最弱 (如图中归一化频率 2,6,10)。从图7和图8的对比可以看出,五步算法比三步算法对振动的抑制能力强。对比图7、图8、图9可以看出,对于振动的抑制能力,七步算法优于三步算法和五步算法。七步算法对移相器标定误差和移相非线性误差也具有很高的免疫能力。
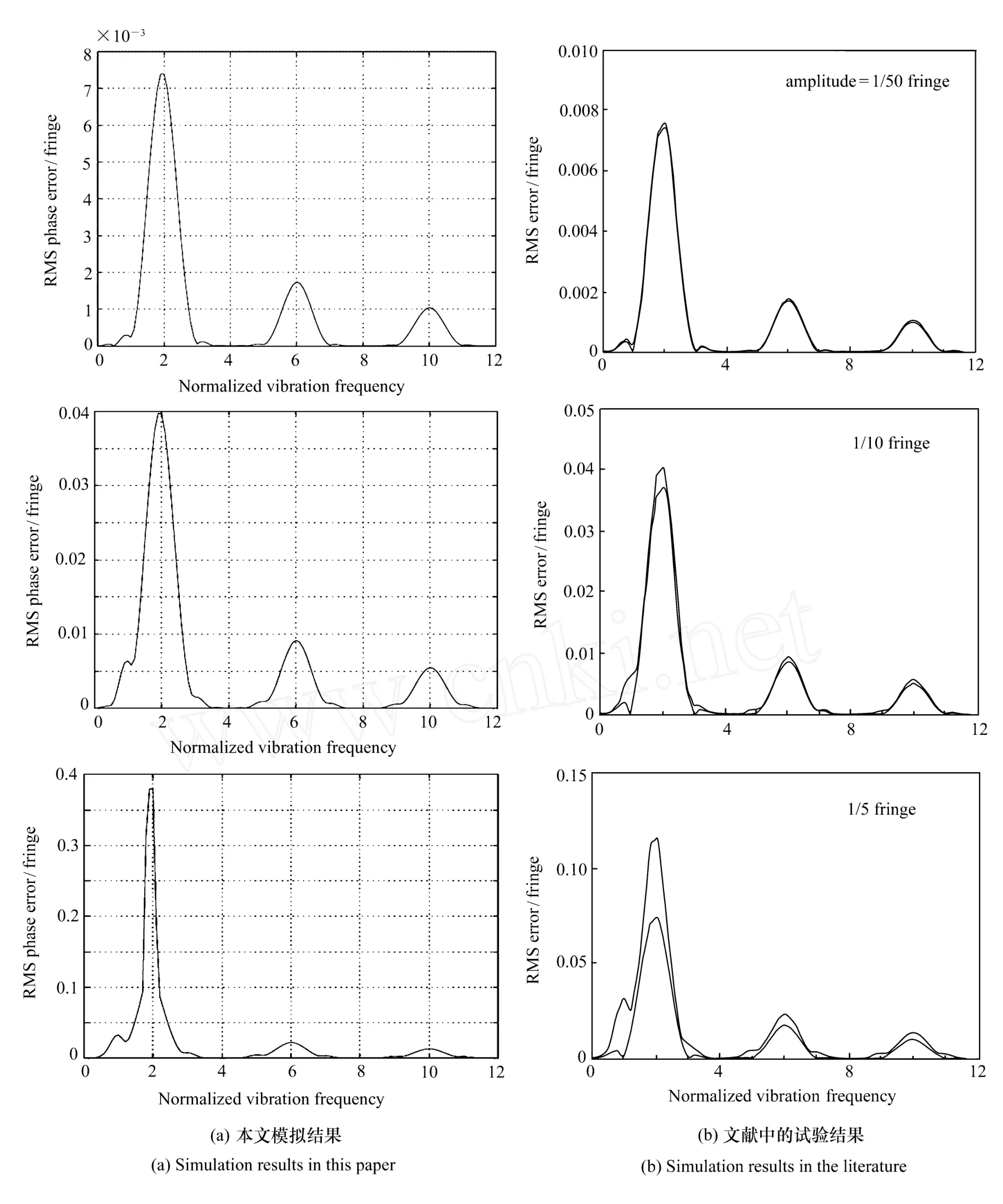
图9 七步算法模拟与试验结果对比:振幅确定,RMS随频率的变化Fig.9 Comparison be tween the resultsof seven-step algorithm and literatures:RMS varies with frequencywhen amplitude is determined
从图7、图8、图9的模拟结果与参考文献对比结果看出两者吻合的较好,所以本文的模拟在预测算法对振动的抑制能力方面具有一定的可信度,能够起到初步评价算法的作用。
6 结 论
在干涉检验过程中,振动对检验精度的影响最大,一般采用主动隔振平台来隔离或减弱振动的影响。在高精度干涉检验中,对抑制振动的需求就更高了,尤其对于低频振动,隔振平台的隔振作用已不明显,需要用算法对振动进行专门处理。本文主要对 Wyant84b三步、Hariharan87五步、七步算法 (移相步距π/2)和十三步算法 (移相步距π/4)等 4种不同移相算法对振动的免疫能力进行了对比分析。分析结果表明,十三步算法对振动的免疫能力最强;振动振幅的大小是影响算法抑制能力的关键,振幅较小的时候,移相算法对振动具有较好的抑制能力。本文的模拟能够合理预测不同移相算法对振动误差的抑制能力,并且在一定程度上能够起到评价和筛选移相算法的作用。
[1] CREATH K.Phase-measurement interferometry techniques[J].Progress Opt.,1988,(26):349-398.
[2] BRUN ING J H,HERR IOTTD R,GALLAGHER J E,et al..Digitalwavefrontmeasuring interferometer for testing optical surfaces sand lenses[J].Appl.Opt.,1974,13(11):2693-2703.
[3] W INGERDEN J van,FRANKENA H H,S MORENBURG C.Linear approximation formeasurement errors in phase shifting interferometry[J].Appl.Opt.,1991,30:2718-2729.
[4] CREATH K.Comparison of phase-measurement algorithms[J].SPIE,1986,680:19-28.
[5] MALACALA D.Optical Shop Testing[M].3rd.Hoboken:A JohnW iley&Sons,Inc.,Publication,2007.
[6] GROOT P,DECKL L.Numerical simulationsof vibration in phase-shifting interferometry[J].Appl.Opt.,1996,35(13):2172-2178.

