Improved PSO algorithm based on chaos theory and its application to design flood hydrograph

Si-fang DONG*, Zeng-chuan DONG, Jun-jian MA, Kang-ning CHEN

1. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering,Hohai University, Nanjing 210098, P. R. China

2. Department of Remote Sensing Center, China Institute of Water Resources and Hydropower Research,Beijing 100044, P. R. China

1 Introduction

The particle swarm optimization (PSO)algorithm was first described by Eberhart and Kennedy (1995). It is a swarm intelligence-based algorithm used to find a solution to an optimization problem in a search space, or to model and predict social behavior in the pursuit of objectives. It has been successfully applied to many optimization problems, including learning artificial neural networks and model predictive control (Eberhart and Shi 2001). A brief and complete overview of the principle, technique, and application of the PSO algorithm is provided by Kennedy and Eberhart (2001)and Clerc (2006). Schutte et al. (2005)used the PSO algorithm for biomechanical optimization and concluded that the performance of the PSO algorithm is superior to that of the genetic algorithm.

Just like other evolutionary algorithms of global optimization, PSO has the disadvantages of premature convergence, delay of convergence in later periods, and an excessive decrease of particle variety with more iterations, which may render it incapable of converging at the global optimal solution. Therefore, domestic and foreign scholars have tried to improve the optimization performance of the basic PSO (bPSO)algorithm and developed some representative improved versions with superior performance. These improved models can be classified into four types: (1)those that balance the global and local searching capabilities of the algorithm by fluctuating or adjusting the parameters of PSO (Angeline 1998; Higashi and Iba 2003); (2)those that improve the performance of the algorithm by designing different types of topological structures (Mendes et al. 2004; Shi and Eberhart 2001); (3)those that decrease the gathering of particles by increasing the particle variety in PSO (Baskar and Suganthan 2004; Kennedy and Eberhart 1997); and (4)those that form a blending algorithm with superior performance by combining PSO with other searching technology (Wang et al.2001; Koay and Srinivasan 2003; Fukuyama and Yoshida 2001).

In order to improve the PSO algorithm, this paper introduces the chaos optimization mechanism and a global particle stagnation-disturbance strategy, which keeps the particles from the stagnation state. An optimal model called the chaos-PSO (COSPOS)model was set up to calculate the design flood hydrograph based on similar disparity theory. In general, the following problems are encountered when using the conventional homogeneous frequency enlargement method to draw the design flood hydrograph: (1)when the flood peak and flood volume relation is not satisfactory, the homogeneous frequency enlargement method might cause different amplification rates in different time intervals of the hydrograph, leading to mutation or discontinuity of hydrographs between successive time intervals; (2)the conventional method simply duplicates the flood discharge in the same time interval, and cannot maintain the original typical flood process after linking each time interval; (3)the hydrograph is smoothed manually, rather than with a computer science technique, which takes more time and effort. In this study, the COSPOS algorithm was used to solve these problems in calculating the design flood hydrograph.

2 Establishment of COSPSO model

2.1 Initialization strategy

The bPSO algorithm initializes the stochastic location of each particle in the solution space. The uniform distribution of particles cannot be guaranteed in this way and more time is needed for the particles to seek the global optimal solution. The particles’ random distribution also increases the randomness of the global optimal solution. If the locations of most particles are significantly inferior to the others, the variety of particles will rapidly decrease as the algorithm runs, ultimately causing prematurity. Therefore, the chaos theory and chaotic optimization mechanism were introduced into the bPSO algorithm to guide the optimal distribution of the particles in the solution space: the locations of the particles were mapped in the optimal chaos space so that particles would stay in the chaos state and move in a chaotic trajectory after they were initialized randomly (Bloch 2005). Most of the particles arrive at a better location within a given period. Therefore, the rational selection of origin remarkably increases the probability that the PSO algorithm will reach the global optimal solution and reduces the number of iterations. At the same time, the diversity of particles does not decrease rapidly during the running of the algorithm, as the particles have a good initial location. We picked two chaos theory mapping methods, Logistic mapping and Ken mapping, for the following analysis:

(1)Logistic mapping is formulated as follows:

where x is the variable (0＜x＜1); f is the self-mapping function; k is the number of iterations ( k = 1, 2,… ,n); and µ is the control parameter (0＜ µ≤4).

(2)Kent mapping and Logistic mapping have a mutual transformation relationship and topological conjugacy property. The formula for Kent mapping is as follows:

where β is the control parameter. Since 0＜β≤1, the Lyapunov exponent of Kent mapping is greater than 0, and the mapping is in chaos status. The chaos invariant set of Kent mapping is (0, 1). However, the chaotic sequence of Kent mapping can easily be influenced by such restraints of the computer as finite word length and accuracy.

2.2 Global particle stagnation-disturbance strategy

An important cause of prematurity of the bPSO algorithm is that the gBest particle that reaches the global optimal solution makes no contribution in the later period, and just follows the velocity and direction of the former iteration in the search. It is easily trapped in a local extremum in a complicated environment with lots of local extrema. No strategy is provided to help it escape from local optimization, but only to force calculation. The chaos theory was introduced to carry out a random disturbance strategy for stagnant gBest particles. The following is an example using Logistic mapping:

The chaos stagnation-disturbance strategy not only guarantees that the algorithm can enhance the ability of the gBest particles to avoid local optimization when the local extremum is close to the global optimal point, but also provides a continuous transform mechanism to help gBest particles escape from local extrema gradually when the local extrema are far from the global optimal point.

2.3 Calculation steps

(1)Two initial numbers of iterations are set as k=1 and k′=1. m chaos variables xi,k+1(i =1, 2,… ,m)with different traces are obtained by assigning xkin Eq. (1)with m initial values, which have slight differences from one another.

(5)If f*is unchanged, we go on to the next step. If not, we return to step (2).

(8)If the global optimal solution remains unchanged for many iterations, then we carry out the disturbance strategy and return to step (2). If not, we go on to the next step.

(9)It is necessary to determine whether f*= f( xi,k′)and xi*= xi,k′comply with the termination rule. If not, then step (6)is repeated. If so, then the optimal solution is found: the optimal solution is x*and the corresponding function is f*.

3 Verification of COSPSO

3.1 Introduction of benchmark functions

In order to evaluate the performance of COSPSO based on chaos theory, including the convergence speed of global optimization, five benchmark optimizations (Table 1)were introduced and analyzed (Runarsson and Yao 2000), facilitating comparison of the performance of COSPSO to that of bPSO. These benchmark optimizations, which aim at a global minimum value, are often used to test the performance of a reformed algorithm. They are composed of two single-peak (unimodal)functions and three multi-peak (multimodal)functions, which possess different characteristics and can thus test every aspect of the optimized performance in various problems.

In Table 1, minF(x)is the global minimum, and f1and f2are consecutive unimodal functions, usually used to inspect the convergence rate of the algorithm. The Rosenbrock function is a typical complex function with a smooth trend, and its global optimal point is in an even, narrow, parabola-shaped valley. It is usually used to test the convergence rate of the algorithm because it requires little information and has a small likelihood of convergence to the global optimal point. f3, f4, and f5are complex nonlinear multimodal functions with plenty of local extrema. Therefore, they work effectively for the inspection of the algorithm’s global search performance, particle diversity, and ability to allow particles to escape from local extrema,guarantee convergence, and prevent prematurity.

Table 1 Five benchmark functions

The functions with more dimensions, wider independent variable scopes, and higher target accuracy are more difficult to be optimized. In order to facilitate the comparison between the original algorithm and the improved algorithm, and to give priority to the performance of the latter, this study selected the most rigorous parameter sets (Eberhart and Kennedy 1995), shown in Table 2.

Table 2 Function parameter settings

3.2 Parameter setting of COSPSO

For better comparison of the performances of COSPSO and bPSO, the same parameter values were used, in addition to some new parameters. In bPSO the tactic of linear dynamic descending within the range of 0.4 to 0.9 was adopted for the inertia weight w(Parsoploulos et al. 2001), while a constant value of w=0.9 was used for the COSPSO.The same value of 2 was used for the acceleration coefficients c1and c2of COSPSO and bPSO. The particle quantity was 30. There were 500 low-accuracy searches and 200 high-accuracy searches in COSPSO. When the control parameter was 4, it could be ensured that Logistic mapping would be in the chaotic state. In this way, the efficient optimization performance of COSPSO was fully examined.

3.3 Unimodal function comparison

Fig. 1 and Fig. 2 show that the performance of COSPSO with the Logistic and Kent mapping functions presents a great improvement over bPSO. In the figures, L-MAP and K-MAP are the processes of COSPOS with Logistic mapping and Kent mapping, respectively,and y indicates the accuracy of iterative calculation. When solving the sphere function,COSPSO always maintains a speedy convergence and could be said to have a tendency of accelerating convergence compared with PSO. The global optimal solution of COSPSO in the initial stage was by no means better than that of bPSO. However, the initial individual value of the particles was much superior to that of randomly initialized bPSO. Therefore, the descending speed of the iterative curve of COSPOS was higher than that of bPSO, thus guaranteeing speed, efficiency, and accuracy in convergence. As seen in Fig. l, it took at least 1 000 iterations before bPSO reached a relatively high convergence accuracy, while in COSPSO only 150 iterations were needed. Furthermore, the accuracy of e-160at the 7 000th iteration of COSPSO was far higher than the accuracy of e-50of bPSO, as shown in Fig. 2.

Fig. 1 Optimization process of Rosenbrock function

Fig. 2 Optimization process of Sphere function

3.4 Multimodal function comparison

In the optimization of multimodal functions (f3, f4, and f5), the abundance of local extrema easily ran the algorithm into local optimization and then caused prematurity, and thus limited the ability of the algorithm to escape from the local extremum and converge at global optimization. Fig. 3, Fig. 4, and Fig. 5 show that the convergence accuracy of COSPSO was the same as that of the bPSO in the Griewank function. However, in other respects, such as the ability to escape from local extrema, convergence speed, and global optimization, COSPSO was evidently better than bPSO. This was well proven by its speedy convergence in the initial 500 to 1 000 iterations. Besides, the initial accuracy of the new algorithm was significantly higher than that of bPSO. All of these factors lead to a global optimal solution. COSPSO can improve the efficiency of multimodal function optimization mainly because of the chaotic optimization process, in which the initial locations of particles are calculated with high accuracy and searching directions are highly precise, thus increasing the variety of particles.The variety does not diminish as iteration continues, and it can enhance particles’ ability to escape from the local extremum, thus avoiding the prematurity in bPSO. This can be seen clearly from the results of the experiment.

Fig. 3 Optimization process of Rastrigin function

Fig. 4 Optimization process of Griewank function

Fig. 5 Optimization process of Schwefel function

4 Design flood hydrograph model

The design flood hydrograph model was established based on complete water level and discharge data from Changba Hydrological Station, 4 500 m upstream of the Wantou hydro-junction, for the period of 1953 to 2004. This model was meant for dealing with the following problems in solving the design flood hydrograph by enlarging a typical flood hydrograph at the same frequency: (1)When the flood peak and flood volume relation is not satisfactory, a mutation on the hydrograph may occur at the connecting point of two successive periods. (2)The original typical flood mode can easily be destroyed (CWRC 2001).Similar disparity theory was applied to establish the object function of the design flood hydrograph model:

The constraint conditions are as follows:

The constrained nonlinear optimization problem of Eq. (6)can be converted into an unconstrained optimization problem by Eq. (8):

where M is a positive even number, which is set as 2 in the following calculation; and σi(i= 1, 2, 3, 4)are the penalty function factors, which are related to the current number of iterations n′. σi(i= 1, 2, 3, 4)is small at the beginning and increases gradually, which is helpful to the search for the optimal solution at a large scale, leading to the final solution to the original question:

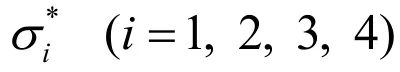
A flood process in 1976 was considered as a typical example. Frequency analysis was carried out based on the long-term hydrological data series and the eigenvalue of a typical flood at Changba Hydrological Station. The typical flood process was mapped with 168 actual measurement points and the time step was one hour. The COSPSO algorithm was applied to draw the design flood hydrograph of Changba Hydrological Station, and, further, to calculate the design flood standard hydrographs of various frequencies.

Some of the COSPSO parameters were set in Section 3.2. In addition, the initial values of penalty function factors were set as σi=5 and=103(i= 1, 2, 3, 4). There were 500 iterations during the whole optimization process and 700 iterations during chaos optimization.

Table 3 shows the eigenvalues of a typical flood and design floods for different frequencies at Changba Hydrological Station. Fig. 6 shows different frequency design flood hydrographs, which basically maintain the distribution pattern of a typical flood process and demonstrate the good effect of curve-fitting.

Table 3 Eigenvalues of typical flood and design floods for different frequencies

Fig. 6 Different frequency design flood hydrographs of Changba Station

5 Conclusions

In COSPSO, a particle’s initial movement trajectory is assumed to be chaotic instead of the desultory stochastic trajectory of other models. The chaos factor is used to guide the particle’s path and a disturbance strategy is used to keep the global particles from stagnation.In the optimization solution tests of two unimodal functions and three multimodal functions,the COSPSO displayed its main advantages, including: (1)speedy convergence to a global optimum solution, (2)high efficiency in the search of particles’ initial direction, (3)refrainment from prematurity, (4)guarantee of particles’ initial variety, and (5)high ability to keep particles from the stagnation state and allow them to maintain chaotic movement.

Based on the similar disparity theory, the scaling model for calculating a design flood was established and a new method of processing penalty function constraints was put forward.In addition, COSPSO, a cluster intelligent algorithm, was applied to optimize the solution,thus radically solving the problems that arise from drawing the design flood hydrograph using the conventional homogeneous frequency enlargement method. With Changba Hydrological Station as an example, the design flood hydrographs for frequencies ranging from 0.05% to 5% were drawn by the flood hydrograph enlargement model with COSPSO. The process is speedy and practical, and the results are in agreement with the typical flood process in 1976.The case study shows that the new method is effective for calculating the peak discharge and flood volumes of the design flood, and that the design flood is consistent with the typical flood patterns. This method allows the user to avoid the randomness and complexity of manual modification.

Angeline, P. J. 1998. Using selection to improve particle swarm optimization. Proceedings of the 1998 IEEE International Conference on Evolutionary Computation, 84-89. Piscataway: IEEE Press. [doi:10.1109/ICEC.1998.699327]

Baskar, S., and Suganthan, P. N. 2004. A novel concurrent particle swarm optimization. Proceedings of the 2004 Congress on Evolutionary Computation, 1, 792-796. Piscataway: IEEE Press. [doi:10.1109/CEC.2004.1330940]

Bloch, D. P. 2005.Complexity, chaos, and nonlinear dynamics: A new perspective on career development theory. Career Development Quarterly, 53(3), 194-207.

Changjiang Water Resources Commission (CWRC). 2001. The Calculation Handbook of Design Flood for Water Conservancy and Hydropower Project. Beijing: China WaterPower Press. (in Chinese)

Clerc, M. 2006. Particle Swarm Optimization. London: ISTE.

Eberhart, R. C., and Kennedy, J. 1995. A new optimizer using particle swarm theory. Proceedings of the 6th International Symposium on Micro Machine and Human Science, 39-43. New York: IEEE Press. [doi:10.1109/MHS.1995.494215]

Eberhart, R. C., and Shi, Y. H. 2001. Particle swarm optimization: Developments, applications and resources.Proceedings of the 2001 Congress on Evolutionary Computation, 1, 81-86. Piscataway: IEEE Press. [doi:10.1109/CEC.2001.934374]

Fukuyama, Y, and Yoshida, H. 2001. Particle swarm optimization for reactive power and voltage control in electric power systems. Proceedings of the 2001 Congress on Evolution Computation, 1, 87-93.Piscataway: IEEE Press. [doi:10.1109/CEC.2001.934375]

Higashi, N, and Iba, H. 2003. Particle swarm optimization with Gaussian mutation. Proceedings of the 2003 IEEE Swarm Intelligence Symposium, 72-79. Piscataway: IEEE Press. [doi:10.1109/SIS.2003.1202250]

Kennedy, J., and Eberhart, R. C. 1997. A discrete binary version of the particle swarm algorithm. Proceedings of the 1997 IEEE International Conference on Computational Cybernetics and Simulation, 5, 4104-4108.Piscataway: IEEE Press. [doi:10.1109/ICSMC.1997.637339]

Kennedy, J., and Eberhart, R. C. 2001. Swarm Intelligence. San Francisco: Morgan Kaufmann Publishers.

Koay, C. A., and Srinivasan, D. 2003. Particle swarm optimization-based approach for generator maintenance scheduling. Proceedings of the 2003 IEEE Swarm Intelligence Symposium, 167-173. Piscataway: IEEE Press. [doi:10.1109/SIS.2003.1202263]

Mendes, R., Kennedy, J., and Neves, J. 2004. The Fully Informed Particle Swarm: Simpler, maybe better.IEEE Transactions on Evolutionay Computation, 8(3), 204-210. [doi:10.1109/TEVC.2004.826074]

Parsoploulos, K. E., Magoulas, G. D., Plagianakos, V. P., Vrahatis, M. N. 2001. Stretching technique for obtaining global minimizers through Particle Swarm Optimization. Proceedings of the Workshop on PSO.Indianapolis: Purdue School of Engineering and Technology, INPUI.

Runarsson, T. P., and Yao, X. 2000. Stochastic ranking for constrained evolutionary optimization. IEEE Transactions on Evolutionary Computation, 4(3), 284-294. [doi:10.1109/4235.873238]

Schutte, J. F., Koh, B. I., Reinbolt, J. A., Haftka, R. T., George, A. D., and Fregly, B. J. 2005. Evaluation of a particle swarm algorithm for biomechanical optimization. Journal of Biomechanical Engineering, 127(3),465-474. [doi:10.1115/1.1894388]

Shi, Y. H., and Eberhart, R. C. 2001. Fuzzy Adaptive Particle Swarm Optimization. Proceedings of the 2001 Congress on Evolutionary Computation, 1, 101-106. Piscataway: IEEE Press. [doi:10.1109/CEC.2001.934377]

Wang, L., Zheng, D. Z., and Li, Q. S. 2001. Survey on chaotic optimization methods. Computing Technology and Automation, 20(1), 1-5. (in Chinese)